Torres de HanóiApenas os preguiçosos não escreveram sobre o famoso jogo de Eduard Luc em Habré. Parece que todas as capas foram arrancadas e algo mais sobre o algoritmo não é mais possível adicionar. Mas não, este tópico tem recursos ocultos. Hoje, em particular, refazeremos o algoritmo para resolver esse quebra-cabeça em uma classificação completa. (Por quê? Apenas por diversão. Sexta-feira possível.)
Este post é dedicado à memória do verdadeiro guru da programação Andrei Mrrl Astrelin, que uma vez me explicou esse algoritmo de maneira simples e inteligível. O pseudo-código abaixo é o texto de sua autoria.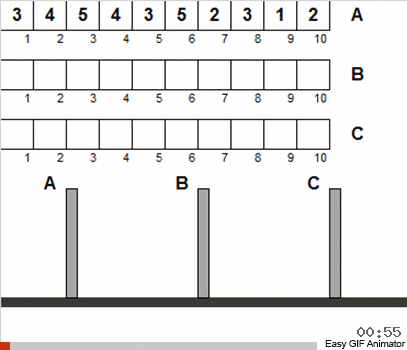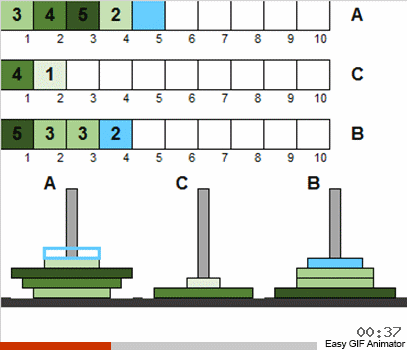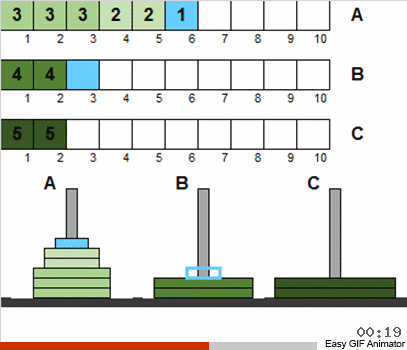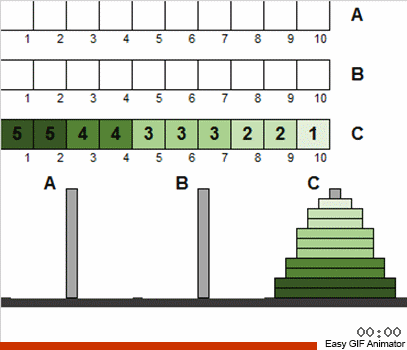
No quebra-cabeça clássico, os discos no primeiro polo são encomendados inicialmente. Mas permitiremos que eles sejam amarrados em qualquer ordem.
Além disso, supõe-se que os tamanhos dos discos sejam únicos. Não vamos nos apegar a essa restrição e permitir repetições.
Se você permitir apenas essas duas liberdades, as condições iniciais do quebra-cabeça podem ser interpretadas como uma matriz (discos são números), e a tarefa se resume ao fato de que essa matriz precisa ser classificada.
As demais condições que (quase) não mudamos:
- Temos dois pólos auxiliares (um par de matrizes vazias).
- Podemos transferir discos um de cada vez.
- Colocando apenas os menores e os maiores (já que permitimos o mesmo tamanho de disco, você também pode colocar o disco movido por cima de outros do mesmo tamanho).
- Temos o direito de comparar um disco portátil com apenas os discos superiores (ou seja, todas as três matrizes são pilhas).
Nossa tarefa: adotar o algoritmo clássico de quebra-cabeças recursivo ...
def hanoi(n, source, helper, target): if n > 0: hanoi(n - 1, source, target, helper) if source: target.append(source.pop()) hanoi(n - 1, helper, source, target)
... e transformá-lo em classificação!
De fato, pelo fato de termos permitido o distúrbio inicial e as repetições para o tamanho dos discos - nada mudou essencialmente a partir disso. Em geral, o problema é resolvido da mesma maneira recursiva clássica. A coisa mais importante a entender é que todos os movimentos do disco são divididos em várias etapas, cada uma das quais é uma miniatura clássica de Hanói.
Ou seja, em cada estágio, não consideramos todos os discos disponíveis, mas apenas a totalidade daqueles que atendem às condições antigas. Depois de classificar este pequeno conjunto pelos clássicos, aproximaremos o estado geral do sistema do quebra-cabeça clássico. Em seguida, pegamos novamente o conjunto de discos que corresponde aos clássicos e aplicamos o algoritmo conhecido novamente. E esse conjunto será maior do que na etapa anterior! E assim repetimos até que todos os discos em todos os polos se tornem repentinamente diferentes do estado clássico.
O sistema que foi violado inicialmente (pelo fato de os discos não estarem ordenados na entrada) é auto-reparável a cada iteração.
Quanto à resolução de repetições, isso não importa. Como os discos idênticos consecutivos, simplesmente nos movemos como um disco.
Algoritmo
Chamamos as colunas
A ,
B ,
C (
A no início não é vazia).
Introduzimos as operações:
A ->
C () - desloque um disco de
A para
C.top (A) ,
top (C) - o tamanho do disco superior
A ou
C. Se a coluna estiver vazia, esse tamanho =
MaxInt .
B ->
C (
K ) - alterna de
B para
C todos os discos cujo tamanho é menor que
K (podemos fazer isso se os discos superiores
A e
C não
forem menores que
K ).
swap () - reorganize as colunas
B e
C (ou renomeie-as - não nos importamos onde estão os discos).
while (
A ) - faça um loop até que
A esteja vazio.
Então, o seguinte algoritmo funciona:
©
MrrlDificuldade
Na pior das hipóteses, a classificação tende a complexidade do tempo para o algoritmo clássico, que, embora simples e elegante, é ao mesmo tempo maximamente ineficiente. Quanto ao melhor e à média, acho difícil assumir.
Quanto à memória, podemos dizer que, se a recursão for usada, os custos serão correspondentes.
Implementação
Eu não escrevi minha própria versão em Python (farei isso mais tarde). No entanto, na seção "Links" abaixo, publiquei alguns links nos quais você pode ver implementações em diferentes idiomas. Opção especialmente interessante em Java. O autor não tomou como base o conhecido método recursivo para resolver o quebra-cabeça, mas construiu a menor árvore de caminhos. Presumivelmente, esta é a solução mais eficaz se você escrever a classificação no estilo de "Torre de Hanói".
Características do algoritmo
Referências
 Torre de Hanói
Torre de HanóiImplementações:
C ,
Java vs C ++ vs Python ,
Python .
Artigos da série:
No aplicativo AlgoLab, essa classificação já está disponível. Embora pertença à classe das classificações por inserções, devido à extravagância do algoritmo, ele é colocado na seção "Outras classificações". Há também uma limitação - os números na matriz classificada podem ser apenas de 1 a 5 (devido à dificuldade de renderização dos discos). Outros números ainda serão substituídos por estes.
Há também um limite no tamanho da matriz - não mais que 20 elementos. Isso é feito exclusivamente para seus próprios interesses - se você escolher uma matriz muito grande, pode ser que seja necessário classificá-la para uma idade muito avançada.

Este artigo foi escrito com o apoio da EDISON Software, uma empresa que desenvolve profissionalmente a iluminação urbana inteligente e mantém sites em Python.