Teoria da felicidade. Acidentes não são acidentais?

Continuo familiarizando os leitores de Habr com os capítulos de seu livro "Theory of Happiness", com o subtítulo "Fundamentos matemáticos das leis da maldade". Este livro de ciências ainda não foi publicado, informando de maneira muito informal sobre como a matemática permite que você olhe para a vida do mundo e das pessoas com um novo grau de consciência. É para aqueles que estão interessados ​​em ciência e para aqueles que estão interessados ​​na vida. E como nossa vida é complexa e, em geral, imprevisível, a ênfase no livro está principalmente na teoria das probabilidades e nas estatísticas matemáticas. Aqui os teoremas não são provados e os fundamentos da ciência não são dados; isso não é de forma alguma um livro, mas o que é chamado de ciência recreativa. Mas é precisamente essa abordagem quase lúdica que nos permite desenvolver a intuição, animar as palestras para os alunos com exemplos vívidos e, finalmente, explicar aos não matemáticos e nossos filhos o que de tão interessante achamos em nossa ciência seca.



Neste capítulo, discutiremos o vôo predeterminado das moedas, mapas topográficos, desastres matemáticos e a natureza da aleatoriedade. E ao longo do caminho, vejamos seções da matemática como a teoria das medidas e a teoria do caos dinâmico.

A conversa sobre as leis da maldade, como uma fonte de turbulência cotidiana, geralmente começa com a famosa lei de um sanduíche . É simplesmente formulado, facilmente verificado e amplamente conhecido:

Um sanduíche sempre deixa cair a manteiga.

É claro que a palavra "sempre" aqui é um exagero. É fácil imaginar as condições em que um sanduíche cairá, deixando o lado oleado intacto. O que as pessoas entendem por essa lei? Muito provavelmente, o sanduíche cai manteiga com freqüência suficiente para torná-lo perceptível. Mas um resultado desfavorável da queda é mais frequente do que favorável? Os sanduíches são diferentes, caem em circunstâncias diferentes, de diferentes alturas ... Existem tantos parâmetros que provavelmente não faz sentido falar sobre padrões em uma tarefa dessas. Tudo pode acontecer. Acontece que ele cai no óleo, depois se torna um insulto, lembramos da lei e lembramos dela. E se o sanduíche ficar desinteressante - com o óleo levantado, ou se ficar sem óleo, não há nada para falar - é claro que a lei é cômica! No final, um sanduíche é como uma moeda, que os matemáticos usam para obter variáveis ​​aleatórias com dois valores possíveis: “águia” e “coroa”. Se a moeda é "honesta", absolutamente não importa de que lado cair, e dizemos que a probabilidade de a águia e a coroa caírem é a mesma e igual $$$1/2$ . Em teoria, sanduíches devem ser os mesmos. Voltaremos a eles no próximo capítulo, mas por enquanto vamos dar uma olhada no mais provável sistema probabilístico simples - a moeda.

Uma moeda em experimentos teóricos da probabilidade é lançada de alguma maneira mágica especial, de modo que a escolha da posição inicial, velocidade inicial e velocidade de rotação durante o sorteio não afeta a probabilidade de um resultado específico. Mas é óbvio que isso é impossível! A moeda é um sistema mecânico e obedece às leis da mecânica, mas elas não contêm variáveis ​​aleatórias. O futuro nas leis do movimento de um corpo tão simples como uma moeda é determinado exclusivamente pelo estado passado desse corpo. Se um robô lança uma moeda, ou o demônio de Laplace é uma criatura mítica que possui informações completas sobre as coordenadas e velocidades de qualquer sistema mecânico, resultados idênticos serão obtidos com dados iniciais constantes. É claro que não somos robôs ou demônios, mas as pessoas realmente jogam moedas tão desleixadas e imprevisíveis que as leis da mecânica podem levar a acidentes?

E de onde, em geral, a aleatoriedade vem no mundo descrito pelas leis da mecânica? De onde vem o acaso? Qual é a diferença entre sistemas verdadeiramente caóticos ou estocásticos, fundamentalmente imprevisíveis, e sistemas nos quais é simplesmente difícil adivinhar o comportamento, mas pode ser calculado?

O problema da moeda foi considerado em 1986 por Joseph Keller. Fornecemos uma explicação simples para a ocorrência de incertezas nesse processo, com base no raciocínio do artigo de Keller. De que lado a moeda vai cair depende do tempo de vôo. $$$t$ e da velocidade angular $$$\ omega$ . Se você medir a velocidade angular em rotações por unidade de tempo, o número de rotações feitas pela moeda é expresso de maneira extremamente simples $$$n = t \ omega$ . Essa dependência define as linhas de um número igual de rotações nas coordenadas $$$(t, \ omega)$ e, por sua vez, limitam as áreas correspondentes a um número par e ímpar de rotações.

Um diagrama mostrando a paridade do número de rotações realizadas por uma moeda em voo. O retângulo mostra a área na qual o processo de previsão da moeda ocorre com mais frequência.

Nesse diagrama, é possível mostrar qual será o resultado de um lançamento de moeda, distorcido por um número conhecido de rotações por segundo e capturado após um tempo de lançamento conhecido. Se cairmos em uma faixa branca, o mesmo lado cairá do topo ao jogar, se estiver em laranja - o oposto. Linhas de velocidade igual são hipérboles e pode-se ver que, à medida que a velocidade aumenta, a alternância de áreas se torna cada vez mais frequente e as próprias áreas se tornam mais finas. A mão humana é imperfeita e uma dispersão muito pequena dos valores iniciais cobre muitas áreas ao mesmo tempo, tornando o resultado imprevisível. No intervalo da mão (o retângulo no diagrama), um deslocamento suficiente $$$5 \%$ pular de uma faixa branca para uma laranja. A questão permanece: como a “honestidade” de uma moeda mecânica real se segue dessa construção? Como obter a probabilidade de perda de uma águia ou coroa do diagrama resultante?

Agir urgentemente!

Vamos nos aprofundar um pouco nas matemáticas que não são ensinadas na escola para entender melhor o que estamos discutindo. Dissemos na introdução que os matemáticos não estudam números ou formas geométricas, como pode parecer depois de estudar um curso escolar. Eles trabalham com estruturas matemáticas (álgebras abstratas, meios anéis, campos, monóides, espaços topológicos e outras coisas abstratas), descrevem-nas, ao que parece, completamente desapegadas à prática, definem-nas, estudam suas propriedades, provam teoremas. E então eles aprimoram suas habilidades em encontrar essas estruturas em vários campos do conhecimento, fazendo descobertas surpreendentemente úteis, inclusive em campos puramente aplicados. Vamos agora abordar um pouco essa matemática e considerar como a base da teoria das probabilidades é construída com base em um conceito muito abstrato de medida.

Descrevemos a mecânica da moeda e obtivemos áreas que descrevem conjuntos de soluções com certas propriedades. Áreas são figuras planas, como passar delas para probabilidades corretamente? Precisamos medir nossas áreas e naturalmente chegamos a elas. Área - é uma medida de uma figura plana. Este é um termo matemático exato para uma função que associa um conjunto a um determinado valor numérico não negativo. Exemplos de medidas são as quantidades em conjuntos enumerados (o número de maçãs em uma sacola, por exemplo), bem como o comprimento , a área e o volume dos números .

Há uma seção inteira na matemática chamada teorias da medida . Essa teoria nasceu na virada dos séculos XIX - XX (Emil Borel e Henri Lebesgue estavam em suas origens) e abriu aos matemáticos amplas oportunidades para analisar objetos muito complexos: conjuntos de cantores e fractal. Ele formou a base da análise funcional e da moderna teoria das probabilidades, cuja base foi lançada pelo notável matemático russo Andrei Kolmogorov. A definição de probabilidade, como medida, permite ver todas as propriedades básicas da probabilidade para conjuntos discretos e contínuos.

Embora nosso livro não seja um livro didático, vale a pena parar um pouco para analisar os conceitos de probabilidade de tório na visão de um pássaro e sentir o gosto da matemática. Para começar, listamos as principais propriedades de qualquer medida. Para imaginá-los melhor, você pode usar as palavras "quantidade" ou "comprimento" ou "área" em vez da palavra "medida".

1. A medida do conjunto vazio é zero.
2. A medida de todo o conjunto mensurável é finita para medidas finitas.
3. A medida do subconjunto não excede a medida do conjunto
4. A medida de união de dois conjuntos arbitrários é igual à soma das medidas desses conjuntos menos a medida de sua interseção (aditividade).
5. A medida de complementar um subconjunto é igual à diferença entre as medidas de todo o conjunto e a medida do subconjunto.

Qualquer função numérica não negativa pode ser uma medida? Nem um pouco. Por exemplo, a idade fornece a uma pessoa um número completamente específico. Mas a idade de duas pessoas não pode ser definida como a soma de suas idades. E a velocidade de corrida não é uma medida - duas pessoas correm não duas vezes mais rápido. Mas momento (momento) ou energia já tem as propriedades de uma medida. O peso, a quantidade de dinheiro, a quantidade de conhecimento, o volume do choro, embora nem sempre sejam coisas facilmente mensuráveis, também podem servir de medida para muitas pessoas.

Em um nível intuitivo, quase todo mundo está familiarizado com o conceito de probabilidade agora. É estimado por cientistas políticos e jornalistas em programas de entrevistas, é discutido o aquecimento global ou a chuva de amanhã, são contadas piadas: Qual é a probabilidade de encontrar um dinossauro no Tver? - Um segundo: seja uma reunião ou não. Na matemática moderna, o conceito de probabilidade é definido como uma medida em um conjunto especial chamado espaço de probabilidade . Inclui eventos elementares e suas combinações obtidas usando as operações de união, interseção e exclusão. Um exemplo de um evento elementar: "perda de um triplo ao arremessar um osso". Um exemplo de um evento que não é elementar: "a perda de qualquer número par, exceto dois". Então, listamos as propriedades da probabilidade:

1. A probabilidade de um evento impossível é zero.
2. A probabilidade para todo o espaço probabilístico é igual à unidade.
3. Se um evento também envolve outro, a probabilidade do segundo não excede a probabilidade do primeiro. Aqui, a relação "implica" para eventos é equivalente a "é um subconjunto" para conjuntos e não significa "é uma causa".
4. A probabilidade de ocorrência de pelo menos um dos dois eventos arbitrários é igual à soma das probabilidades de cada um desses eventos, menos a probabilidade de que os eventos ocorram simultaneamente.
5. A probabilidade de um evento não ocorrer é um menos a probabilidade de um evento ocorrer.

Dê uma olhada nas propriedades das medidas e probabilidades e você verá que estamos falando das mesmas propriedades.

Nem todas as propriedades de probabilidade surgem de sua definição como uma medida: os conceitos de independência de eventos e o método de calcular a probabilidade de dois ou mais eventos independentes simultaneamente, à medida que produtos de probabilidades são introduzidos por probabilidade condicional , mas esses conceitos são consistentes com a definição de Kolmogorov.

Variáveis ​​aleatórias discretas correspondem a conjuntos contáveis ​​finitos; neles, uma medida natural é uma contagem comum do número de elementos. Consequentemente, a probabilidade em um espaço probabilístico discreto é o cálculo combinatório de opções familiares a todos os alunos. Para variáveis ​​aleatórias contínuas, a probabilidade, como medida, é mais parecida com comprimento ou área, e aqui estamos falando de densidades de probabilidade .

A analogia de probabilidade com a medida não termina aí. Qual é o valor médio ? Este é um análogo da posição do centro de massa de uma figura que consiste em massas pontuais ou em um sólido com uma densidade conhecida. E essas quantidades são calculadas da mesma maneira. E como é caracterizada a dispersão de variáveis ​​aleatórias em torno da média: variância ? Assim como o momento de inércia caracteriza a distribuição de massa ao redor do centro de massa. E, novamente, as fórmulas para calcular a variação para uma amostra ou distribuição coincidem com as fórmulas para o momento de inércia de um conjunto de corpos ou de um corpo sólido com uma forma astuta.

A propósito, se substituirmos nas definições e propriedades da probabilidade a soma por "máximo" e o produto por "mínimo", então podemos construir uma teoria alternativa, chamada teoria das possibilidades . É assim que a matemática funciona. Começamos com o raciocínio abstrato: os números formam uma álgebra com operações de adição e multiplicação, mas em um intervalo de número limitado, você pode construir uma álgebra semelhante com operações de mínimo e máximo. Construímos o conceito de medida em uma nova álgebra e descobrimos que ela abre uma nova visão do mundo! Em contraste com a teoria da probabilidade, em tal teoria duas medidas coordenadas podem ser construídas - a possibilidade e a necessidade e, diferentemente da probabilidade, elas estão de acordo com as operações de combinação e interseção de eventos. Essa direção foi criada pelo americano Lotfi Zadeh, um azerbaijano de origem, serve como base para a lógica nebulosa e é usada no reconhecimento automático de padrões e nos sistemas de tomada de decisão.

Incrível, mas é verdade!

A primeira propriedade das medidas parece trivial, mas é interessante em sua assimetria. Se a medida do subconjunto for zero, isso não significa que está vazio! Por exemplo, uma linha é um subconjunto dos pontos em um plano, mas sua área (medida) é zero. Existem exemplos mais exóticos - conjuntos de cantores e fractais, com uma estrutura complexa, contendo um número infinito de pontos, “visualmente” ocupando uma determinada área ou volume, mas mesmo assim com zero medida.

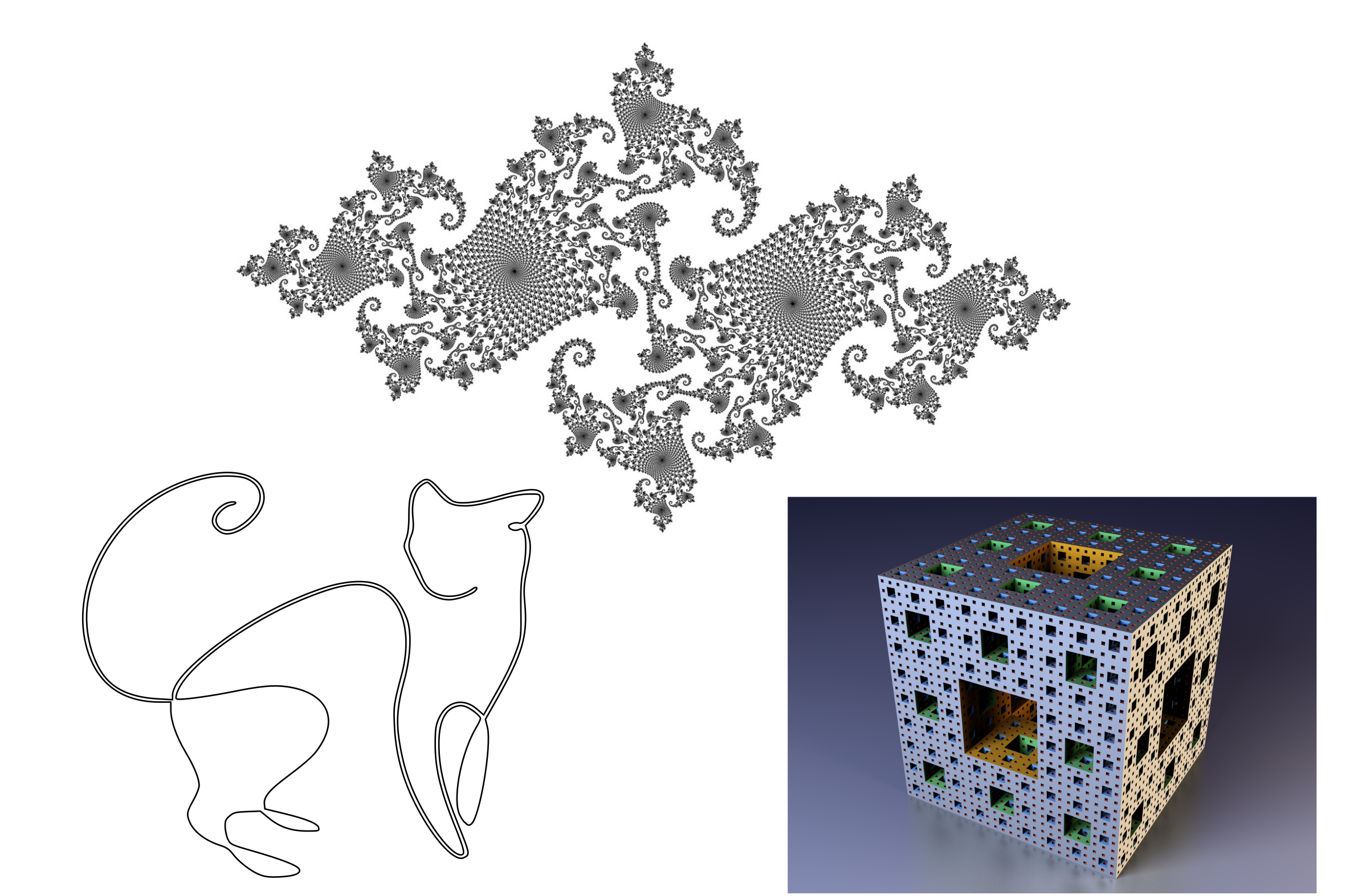Alguns objetos de zero medida: uma linha em um plano, conjunto esporádico de Julia, esponja fractal de Menger.

Ao preparar esta ilustração, encontrei uma imagem maravilhosa de um conjunto desconectado de Julia em um fundo transparente com alta resolução. Depois de inseri-lo no editor de vetores, me deparei com uma dificuldade engraçada - era muito difícil entrar nessa imagem com o mouse para selecioná-la. É tão "flexível" que a probabilidade de entrar em um pixel preenchido era visivelmente menor do que entrar em um fundo transparente. No espaço de probabilidade, subconjuntos de medida zero também podem existir, mas isso não significa que os eventos desses subconjuntos sejam impossíveis. Da quarta à quinta tentativa, eu ainda podia selecionar a imagem, pois os pixels têm um tamanho finito. Mas o que aconteceria se eu tivesse à minha disposição um conjunto incoerente de Julia com resolução infinita?

Imagine que você esteja usando um gerador de números aleatórios de software que produz um número real arbitrário a partir de $$$0$ antes $$$1$ . Qual é a probabilidade de um número cair $$$0$ ? e números $$$1/2$ ou $$$e / \ pi$ ? Em todos esses casos, a resposta será zero! Em vez disso, o menor número positivo disponível para o computador, a chamada máquina epsilon, porque o computador opera com um número finito de casas decimais. Espere, você diz, em que sentido é zero? Os mesmos números não são impossíveis. Vamos conduzir um experimento, como resultado, obtemos um número específico e, quando o obtemos, então "por construção" a probabilidade de sua aparência não pode ser zero. É isso mesmo, mas quanto tempo devo esperar até que exatamente 0 saia? Quase infinitamente! O fato é que um único número, como um ponto em um segmento, tem zero medida e uma probabilidade zero honesta. Apenas uma medida de um segmento contínuo, mesmo que muito pequeno, é diferente de zero. Portanto, não estamos falando de probabilidade, mas de densidade de probabilidade, que, quando multiplicada por uma medida finita de um subconjunto em um espaço de probabilidade, fornecerá um valor finito - a probabilidade de cair nesse subconjunto. Aliás, o gerador de números aleatórios ideal com precisão infinita é a probabilidade de obter um número racional (não um pouco concreto, mas qualquer) com ele também será zero. A prova de que números racionais formam um denso subconjunto de medida zero do conjunto de números reais fez barulho no final do século XIX.

Se alguém pacientemente realizar mil experimentos com uma moeda e felizmente lhe disser que ele conseguiu tantas “águias” quanto ele “caudas”, você pode expressar dúvidas com segurança ou parabenizá-lo por uma sorte rara. Embora jogar uma moeda e um processo aleatório discreto, à medida que as estatísticas se acumulam, o poder do espaço de probabilidade aumentará e a medida do evento: "o número de" águias "coincide com o número de" caudas "" diminuirá. Pode-se demonstrar, usando a fórmula de Stirling, que a probabilidade desse evento “mais provável” tende a zero com um aumento no número de testes conforme $$$1 / \ sqrt {\ pi n}$ . Para cem elencos, isso é um pouco mais de cinco por cento, para dez mil - apenas meio por cento. Nesses casos, os matemáticos dizem: quase certamente o número de "águias" não será igual ao número de "caudas" . Por mais estranho que pareça, mas “quase certamente” é um termo matemático exato, o que significa que o evento é um complemento de um subconjunto do espaço de probabilidade da medida zero. , , : .

. ( ) ( «» «» ). , , .

! ( ). , , . $$$\omega = n/t$ . $$ω = 1 / t é igual$\omega = 1/t$$$S , devido à propriedade de aditividade, a área sob a curva$S$$$ω = n / t será igual$\omega = n/t$$$$S_n = n S$ . Por sua vez, para tiras individuais, obtemos: $$$S_{n} - S_{n-1} = n S - (n-1)S = S$ .Acontece que a diferença de área não depende do "número" da hipérbole. Isso não é algo especial em relação à hipérbole; a mesma conclusão pode ser tirada para qualquer curva da forma$$$y = n f(x)$ , $$$f$ . , , , «» .

, , , , . , .

, , . , $$$20$ $$$40$ , — . . , , , , $$$50.6\%$ .

2007 , . , , , — , , « », «» .

? , ? , , , , : $$σμ=σ/√n aqui$\sigma_{\mu} = \sigma/\sqrt{n}$$$σ é o desvio padrão para a distribuição estudada. No nosso caso, para a distribuição de Bernoulli com probabilidade$\sigma$$$0,51 que é igual$0.51$$$$\sqrt{0.51\times0,49}\approx0.5$ . Para identificar com confiança o desvio da média de um centésimo, esse desvio deve exceder $$3 desvios padrão. Assim, podemos estimar o número de tentativas:$3$

$$

$$n = \left(\frac{\sigma}{\sigma_{\mu}}\right)^2 = \left(\frac{3\times0.5}{0.01}\right)^2 \approx 22500$$

, . , , «», , , . $$$40000$ «». «» «» , , , , .

.

, $$$20000$ «» . , , — .

, , , :

, , , .

, , . — , . $$$\alpha$ $$$S$ , , . , - $$$d$ , . . $$$\alpha=0.5\%$ .

«» . 40 , 3 .

$$$d = \sqrt{\alpha S}$ . $$$d \sqrt{S} = S\sqrt{\alpha}$ . , , , , , . $$$d^2 = \alpha S$ . Dobrando o cartão para que ele despeje $$$n$ horizontal e $$$m$ curvas verticais, obtemos a área total da zona desagradável igual a: $$$S (n + 2) \ sqrt {\ alpha} + S (m + 2) \ sqrt {\ alpha} -S (n + 2) (m + 2) \ alpha$ . Levando-o para a área de todo o mapa, obtemos uma parcela desagradável da área total:

$$

$$p = (n + m + 4) \ sqrt {\ alpha} - (n + 2) (m + 2) \ alpha.$$

A figura mostra as áreas em que essa proporção excede $$$50 \%$ para vários valores $$$\ alpha$ .

Áreas nas quais há uma maior probabilidade de estar na dobra do mapa ou na sua borda. Os números indicam a fração da área da vizinhança considerada da área de todo o mapa.

Acontece que um cartão dobrado ao meio duas vezes já pode ser considerado formalmente desonesto em relação a um turista. Na maioria das vezes, os cartões têm três dobras verticais e três horizontais, o que fornece a probabilidade de cumprir a lei da maldade com uma probabilidade de aproximadamente $$$60 \%$ às $$$\ alpha = 0,5 \%$

De onde vem o acaso?

Nas lojas de souvenirs, você encontra pêndulos magnéticos para a "escolha dos desejos". Eles também são geradores aleatórios mecânicos e às vezes são erroneamente chamados de "pêndulos caóticos". Iniciando o movimento a partir de uma posição e velocidade iniciais, o pêndulo realiza uma série de oscilações "imprevisíveis" e, finalmente, para em um dos setores. No entanto, as flutuações aqui não são imprevisíveis, são simplesmente muito sensíveis às condições iniciais. Para cada setor em que o pêndulo pode parar, há uma região de atração no espaço de velocidade de coordenadas. Este é um conjunto dessas condições iniciais sob as quais o pêndulo se atrairá necessariamente a um determinado ponto no setor indicado. O ponto de parada do pêndulo é chamado de atrator - um ponto de atração. No caso de um pêndulo da imagem, o espaço de coordenadas e velocidades é quadridimensional e, portanto, não é fácil mostrar a área de atração. Mas se nos restringirmos a apenas dois setores e reduzirmos o problema a unidimensional (esse pêndulo é chamado de oscilador de Duffing), o espaço dos valores iniciais se transformará em um plano, para que as regiões de atração possam ser vistas. Eles se parecem com um intrincado símbolo Yin-Yang, transformando-se rapidamente em faixas estreitas que separam as áreas de atração.

Áreas de atração de atratores para um pêndulo unidimensional de desejos - o oscilador Duffing.

Como no caso da moeda, mudando ligeiramente as condições iniciais, passamos de um atrator para outro. Dados e roleta funcionam da mesma maneira, mas eles próprios não são geradores aleatórios. Estes não são sistemas verdadeiramente caóticos e seu comportamento pode ser calculado com precisão.

Mas qual é a chance real? Um bom exemplo de um verdadeiro sistema estocástico é o aparecimento de carros na estrada. As pessoas não concordam, não coordenam seus planos, cada elemento do conjunto fora da estrada age de forma independente. E, embora existam certos padrões no comportamento das pessoas - horas de ponta pela manhã e à noite, estradas vazias à noite etc., não temos e nunca teremos informações suficientes sobre cada participante do movimento para prever a aparência de qualquer uma delas. A mecânica das partículas elementares no nível quântico, a deterioração dos átomos instáveis, as mudanças no código genético, provavelmente os terremotos e as cotações da bolsa de valores também são estocásticos. A única coisa que resta para o pesquisador é considerá-las como variáveis ​​aleatórias e descrevê-las em termos da teoria das probabilidades.

Mas há outra fonte de chance - o caos dinâmico . Os sistemas caóticos diferem dos estocásticos, pois são descritos por equações e parâmetros exatos que não contêm aleatoriedade. No entanto, seu comportamento não é apenas complicado, mas caótico e verdadeiramente imprevisível. Se começarmos a oscilar o pêndulo dos desejos, com muito cuidado, com frequência e amplitude controladas com precisão, descobriremos que seus movimentos suaves não podem ser calculados por um longo tempo. Nenhum algoritmo em computadores arbitrariamente precisos nos permitirá calcular o comportamento exato do pêndulo para um futuro arbitrariamente distante. Ele não para em nenhum setor, mas faz movimentos suaves, mas nunca volta ao mesmo ponto no espaço de velocidade de coordenadas duas vezes. Outro exemplo de um sistema caótico extremamente simples é uma bola ideal quicando no campo de gravidade em uma mesa ideal com uma mola. As equações relativamente simples de Lorentz mostraram que nunca podemos prever o tempo por mais de duas semanas - esse também é um sistema caótico.

A teoria do caos dinâmico foi capaz de explicar a natureza dessa imprevisibilidade. O simples pêndulo unidimensional dos desejos, que examinamos, tinha dois pontos estacionários estáveis ​​- dois atratores e um instável, dos quais o sistema está tentando escapar - é mostrado por um círculo branco. No modo caótico, em vez de um conjunto de atratores, um número infinito de trajetórias estacionárias instáveis ​​aparece no sistema. Esse conjunto é infinito, mas tem zero medida e é uma estrutura disjunta muito complicada. Uma vez em uma dessas trajetórias, em princípio é impossível segui-la usando algoritmos finitos. Mas o mais surpreendente foi que esse número infinito de trajetórias instáveis ​​em si é atraente! 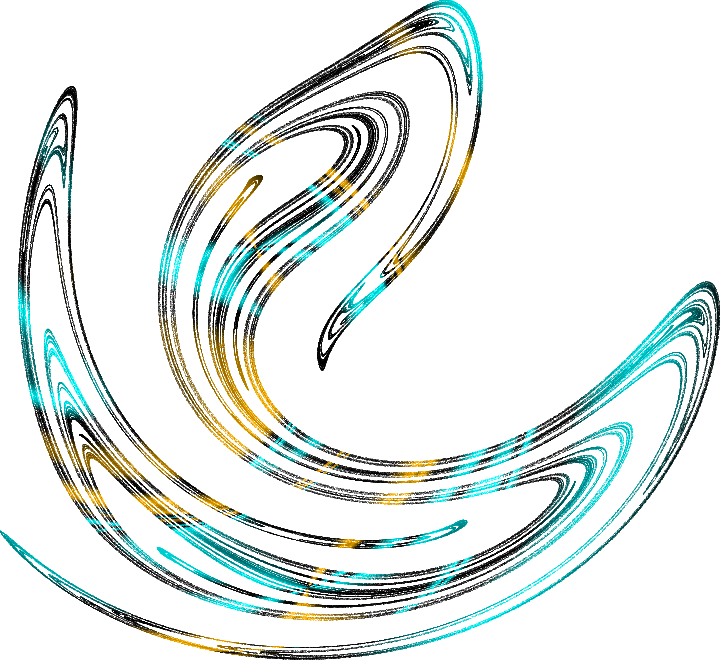O sistema caótico salta continuamente da vizinhança de uma trajetória instável para outra, permanecendo o tempo todo dentro dos limites desse atrator estranho. Então esses conjuntos são chamados: atratores estranhos . É assim que a seção de um atrator estranho para um pêndulo de desejos, sujeita a oscilações harmônicas, parece fascinantemente bonita. Este objeto para um pêndulo unidimensional pode ser descrito no espaço tridimensional (coordenada, velocidade, fase da oscilação forçada). Se você cortar um atrator neste espaço por um avião, poderá ver sua estrutura, isso é chamado de seção Poincare . Cada ponto aqui é um traço da trajetória, e a cor dos pontos reflete a velocidade relativa com a qual as trajetórias se dispersam. Aqui estão alguns belos atrativos estranhos:


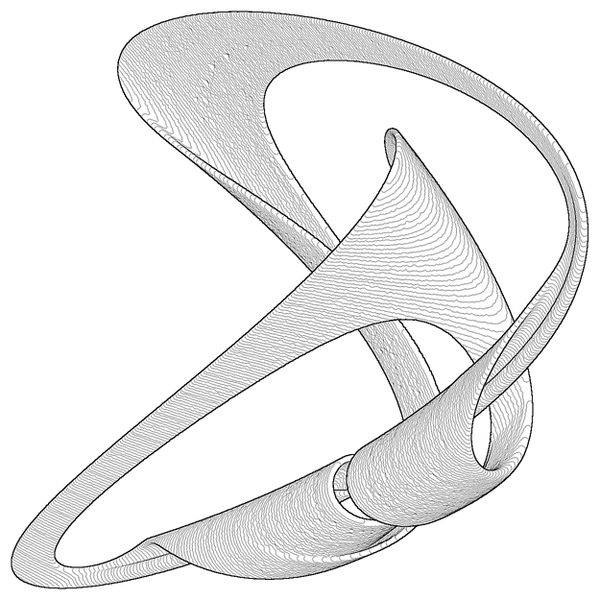Esquerda: seção Poincare para a trajetória de uma bola quicando em uma mesa com mola. Muitos pontos pertencem à superfície da esfera correspondente à lei de conservação de energia. Direita: uma região volumétrica que encerra um atrator estranho que nasce durante vibrações forçadas de uma chapa grossa.

A suavidade da trajetória caótica permite que você olhe um pouco para o futuro. Isso explica uma observação irritante: por um lado, os meteorologistas às vezes não conseguem prever com confiança o tempo por uma semana, mas, por outro, se você disser que amanhã será o mesmo tempo que hoje, não será enganado em cerca de três em cada quatro casos . Em geral, as piadas sobre meteorologistas são injustas e devemos prestar homenagem ao pensamento e à perseverança humanos, que tornaram possível prever o clima em um nível moderno!

O caos dinâmico é muito complexo e bonito como teoria; dá origem a imagens de incrível elegância, mas também pode ser útil. Por exemplo, os algoritmos pelos quais números aleatórios são gerados em computadores também são determinísticos. Para os exemplos deste livro, usei um gerador de números pseudoaleatórios que não iniciou o processo estocástico real (decaimento alfa ou contagem de carros na estrada), mas calculei o próximo número "aleatório" com base nos números anteriores que ele recebeu anteriormente.

De moedas a borboletas e o próprio destino

Observações de como pequenos desvios se transformam em mudanças globais no sistema levam ao pensamento do "efeito borboleta". Deixe-me lembrá-lo de que esse efeito significa uma cadeia de conseqüências dramáticas de longo alcance de algum evento insignificante, à primeira vista. Esmagada por pesquisadores do passado, a borboleta no conto de Ray Bradbury "E o trovão atingiu" levou a uma reestruturação radical do futuro. E uma de suas palestras, Edward Lorenz, criador da teoria do caos dinâmico, intitulada: "Um bater da asa de uma borboleta no Brasil pode causar um tornado no Texas?"

Nós implicitamente nos referimos a esse efeito, lamentando: "Se eu não tivesse virado a esquina, tudo teria sido diferente!", "Se ele não tivesse embarcado neste trem, não haveria catástrofe!" ou "Por causa de tais insignificâncias, eles brigaram e se separaram !!" Mas vemos que um mundo quântico verdadeiramente estocástico e relógios atômicos ultra-precisos coexistem no mundo, sistemas hamiltonianos estáveis ​​no mundo das estrelas e galáxias e o caos dos anéis de Saturno ou Kuiper, o movimento térmico das moléculas e a incrível precisão da operação de sistemas biológicos ou mecanismos automóveis. Não, o bater da asa de uma borboleta não dá origem a furacões, mas desaparece sem deixar rasto, dando origem a uma cadeia de vórtices que transmitem energia e informação a vórtices cada vez menores, até que energia e informação desapareçam no caos das flutuações. Deve-se entender claramente que pequenos desvios levam a uma reorganização fundamental do sistema apenas se ele for instável ou se o sistema estiver à beira de uma bifurcação ou catástrofe - é assim que a reestruturação global no comportamento do sistema com pequenas mudanças de parâmetros é chamada na linguagem da matemática. E as bifurcações sempre formam conjuntos de medidas zero no espaço de parâmetros - esses são pontos ou limites. Pequenos distúrbios não levam a desastres em quase todos os lugares (este também é um termo exato que significa "em todos os lugares, exceto por um conjunto de medidas zero"), e estados instáveis ​​na natureza raramente são observados sem passar no "teste do tempo".

Se o casal se separou "por causa de um disparate", ela estava destinada a se separar em qualquer caso, ela era instável. Casais estáveis ​​passam por guerras e fomes e, às vezes, terminam, mas não por brincadeiras, mas como resultado de mudanças profundas que podem acontecer a uma pessoa durante sua vida. Na cadeia de eventos que levou ao acidente de trem, não é fácil destacar um evento-chave (um erro específico ou acidente fatal) e, muito provavelmente, a chave não é um evento, mas uma violação sistemática das regras, levando o sistema a um estado instável. Se existem muitos parâmetros no sistema, e alguns são aleatórios, e nossa vida é estruturada dessa maneira, as informações nesse sistema tendem a se perder, e não será possível restaurar no momento exato da nossa vida que "tudo deu errado". Não se atormente com arrependimentos sobre o que aconteceu, mas observe mais de perto o que está acontecendo com você agora, para não perder o verdadeiro ponto da bifurcação.

Nesse sentido, podemos lembrar uma das leis da merfologia, chamada lei de restauração por um certo Dreisen:

O tempo de melhoria da situação é inversamente proporcional ao tempo de sua deterioração.

A seguinte observação é dada como exemplo: Leva mais tempo para colar o vaso do que para quebrá-lo. Esta lei descreve surpreendentemente com precisão a relação entre as taxas características para o processo de relaxamento de um sistema estável, que pode ser descrito por uma lei exponencial decrescente $$$e ^ {- \ lambda t}$ e a taxa de desenvolvimento do processo catastrófico em um sistema instável, na aproximação linear - o crescimento exponencial de uma pequena perturbação $$$e ^ {\ lambda t}$ . Essas velocidades são de fato inversamente proporcionais entre si. O exemplo do vaso, no entanto, não é relaxamento - uma transição para o estado mais provável. Está mais próximo de outro processo - a auto-organização , esse processo, como primeira aproximação, é descrito pela lei logística e mais próximo em velocidade de relaxamento do que de desastre.

Processos não estacionários típicos: desastre, relaxamento e auto-organização, com o mesmo tempo característico.

$$

$$* * *$$

Às vezes, andando na neve, fico surpresa que um floco de neve caia no meu nariz. Estou surpreso que a probabilidade desse evento fosse insignificante. A julgar por isso, ela nasceu no céu, sobre o Oceano Pacífico, circulou em turbulentas correntes turbulentas na nuvem, caiu continuamente mudando de direção ... para chegar à ponta do meu nariz! E que caminho impressionante os fótons viajaram de uma estrela distante!? Por dezenas de milhares de anos eles correram pelo Universo, não foram engolidos por poeira, não encontraram um asteróide! Eles nasceram no mundo quântico de uma estrela distante e terminaram sua jornada no mundo quântico da proteína opsina na retina do meu olho. Não faz sentido sequer considerar a probabilidade desse evento, é zero, mas o evento acontece e vejo a luz tremeluzente de uma estrela. Agora está claro que isso é tudo porque a área do meu nariz e até as moléculas têm uma medida diferente de zero, mas ainda assim incrível: o que quase certamente não deveria ter acontecido ainda está acontecendo!

Que os filósofos discutam sobre o destino predeterminado ou acidental, a verdade ou o fantasma de nosso conhecimento da natureza. Exorto o leitor a olhar para o mundo do alto das abstrações matemáticas e admirar sua beleza e consistência.