Lógica de três valores
Lista de realizações
- Portas lógicas ternárias básicas: T_NOT, T_OR, T_AND, T_NAND, T_NOR, T_XOR e mais
- Síntese, Minimização e Realização para Funções Ternárias
- Meio adicionador ternário, somador completo ternário, ondulação ternária
- Subtrator completo ternário, comparador, multiplicador, multiplexador / desmultiplexador
- Chinelos e patas de aleta ternária
- Uma Unidade Aritmética e Lógica Ternária (ALU) primitiva
Convenções e tecnologias usadas
- Ternário desequilibrado (0, 1, 2) foi usado na implementação
- 1 Trit é expresso por 2 bits: 0 ~ 00, 1 ~ 01, 2 ~ 10 (11 é indefinido)
- ModelSim, Quartus prime, Logisim
1. Introdução
Como alunos do primeiro ano da Universidade de Innopolis, tivemos a oportunidade de realizar projetos em todo o curso de arquitetura de computadores. Nosso grupo estava particularmente interessado no sistema ternário e em seu funcionamento, por isso decidimos implementar um sistema ternário simples com componentes básicos (portões).
Na lógica, uma lógica de três valores (também lógica trinária, trivalente, ternária) é um dos vários sistemas lógicos de muitos valores nos quais existem três valores de verdade indicando verdadeiro, falso e algum terceiro valor indeterminado.
A lógica ternária é compatível com MVL (lógica de valores múltiplos). No entanto, apenas três estados lógicos são usados, ' 0 ', ' 1 ' e ' 2 '. A raiz ótima ( r ) de um número fracionário é o logaritmo natural ( e ). A lógica ternária usa representação numérica com r = 3 , em comparação com a lógica binária que usa r = 2 , portanto, a raiz inteira mais econômica que é a mais próxima do logaritmo natural e é a base 3. Essa propriedade especial da base 3 inspirou os primeiros computadores. projetistas para construir um computador ternário.
O primeiro computador ternário em funcionamento foi construído na Rússia na Universidade Estadual de Moscou em 1958. O computador foi projetado por Nikolay Brusentsov e seus colegas. Eles chamaram Setun , como o rio que corre perto do campus da universidade.
Lógica ternária
Uma função lógica ternária é um mapeamento F: {0,1,2} n -> {0,1,2} . Discutiremos as vantagens e desvantagens da lógica ternária sobre a lógica binária.
Onde a lógica booleana possui 2 2 = 4 operadores unários, a adição de um terceiro valor na lógica ternária leva a um total de 3 3 = 27 operadores distintos em um único valor de entrada. Da mesma forma, onde a lógica booleana possui 2 2 2 = 16 operadores binários distintos (operadores com 2 entradas), a lógica ternária possui 3 3 2 = 19.683 desses operadores. Onde podemos nomear facilmente uma fração significativa dos operadores booleanos (não, e, ou, nand, nem, exclusividade ou equivalência, implicação), não é razoável tentar nomear todos, exceto uma pequena fração dos possíveis operadores ternários.
Vantagens da lógica ternária
Uma representação lógica ternária permite uma codificação de informações mais compacta e eficiente do que a representação lógica binária equivalente. O argumento exposto é o seguinte: se assumirmos que um circuito digital possui N combinações de entradas possíveis, um circuito binário requer linhas de entrada de 2 N e um circuito ternário requer 3 linhas de entrada de N.
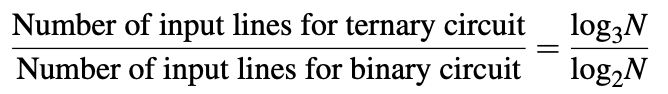

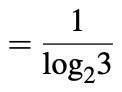

Portanto, uma implementação codificada ternária de uma determinada função lógica binária deve exigir 0,63 vezes as linhas de entrada que a implementação binária correspondente.
Desvantagens da lógica ternária
Embora os circuitos lógicos ternários devam exigir menos linhas de entrada do que os circuitos lógicos binários equivalentes, atualmente, os circuitos lógicos ternários não são uma opção prática. As razões são
- A tecnologia de implementação de hardware ternário ainda está nos níveis teórico, de simulação e de teste de laboratório
- A representação de três níveis lógicos ternários (0, 1 e 2) usando níveis de tensão da tecnologia existente ainda não está efetivamente definida
- Nenhum modelo computacional e linguagem de programação são desenvolvidos. No entanto, simulando resultados da implementação de circuitos ternários usando tecnologias de semicondutor de óxido metálico complementar (CMOS), diodo de tunelamento ressonante (RTD) e nanotubos de carbono, demonstrando que a lógica ternária pode ser uma opção para computação futura.
Várias representações possíveis para o sistema ternário
- Sistema de numeração ternária (ternário não balanceado) , cada dígito é um trit (dígito trinário) com um valor de: 0, 1 ou 2
- Ternário equilibrado , cada dígito tem um dos 3 valores: −1, 0 ou +1; esses valores também podem ser simplificados para -, 0, +, respectivamente (mais comumente usado)
- Representação binária redundante , cada dígito pode ter um valor de -1, 0, 0/1 (o valor 0/1 tem duas representações diferentes)
- Sistema de números binários inclinados , apenas o dígito diferente de zero mais significativo tem um valor 2 e os dígitos restantes têm um valor de 0 ou 1
Mais sobre o sistema de numeração ternária equilibrado
Hoje, quase todo o hardware é projetado para computação binária. Se tivéssemos um componente eletrônico estável com três estados estáveis, o mundo talvez tivesse se voltado para a computação ternária. No entanto, essa não é a verdade hoje. A notação de raiz ternária balanceada possui algumas propriedades benéficas:
- A inversão ternária é fácil, basta trocar -1 com 1 e vice-versa. Se usarmos um exemplo, 24 é representado como 1T0 e -24 como T10 em notação ternária balanceada (T é simplesmente uma notação para -1). Isso é mais simples que a regra para o complemento dos dois na lógica binária.
- O sinal de um número é dado por seu 'trit' diferente de zero, mais significativo
- A operação de arredondamento para o número inteiro mais próximo é idêntica ao truncamento.
- Adição e subtração são essencialmente a mesma operação (ou seja, você apenas adiciona os dígitos usando as regras para adição de dígitos)
Exemplos:
21 10 = 1T10 3 ; 296 10 = 11T00T 3 ;
-24 10 = T10 3 ; -137 10 = T110T1 3
Aritmética ternária
A aritmética ternária pode oferecer uma notação mais compacta que a aritmética binária e teria sido uma escolha óbvia se os fabricantes de hardware encontrassem um comutador ternário.
Adição e multiplicação ternárias equilibradas
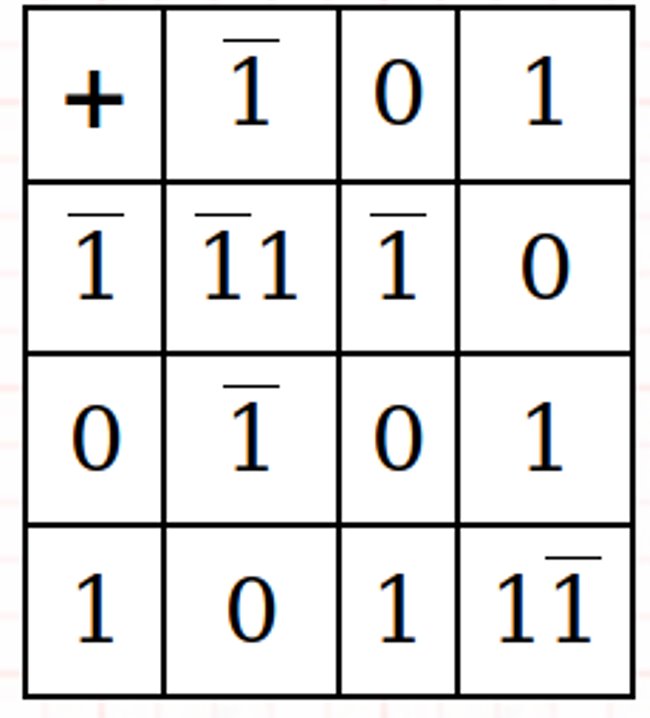
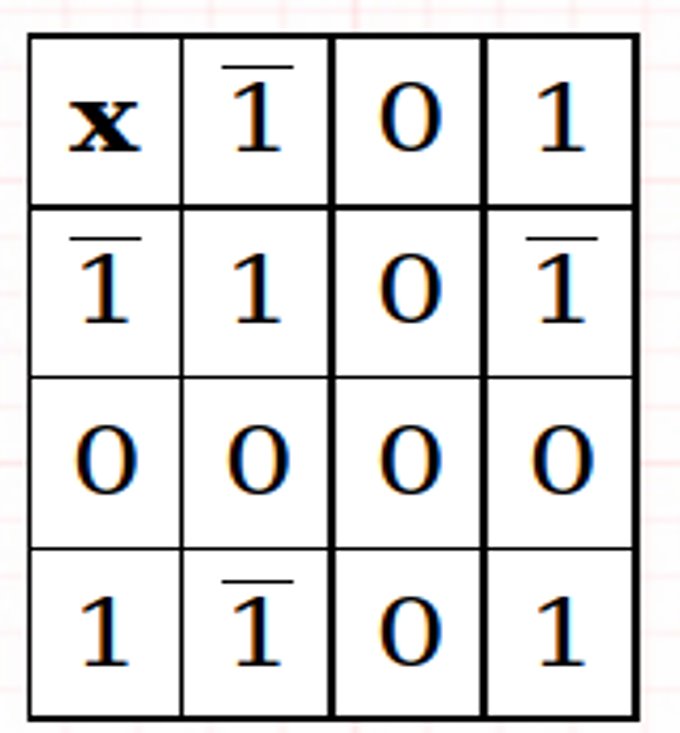
Exemplos:
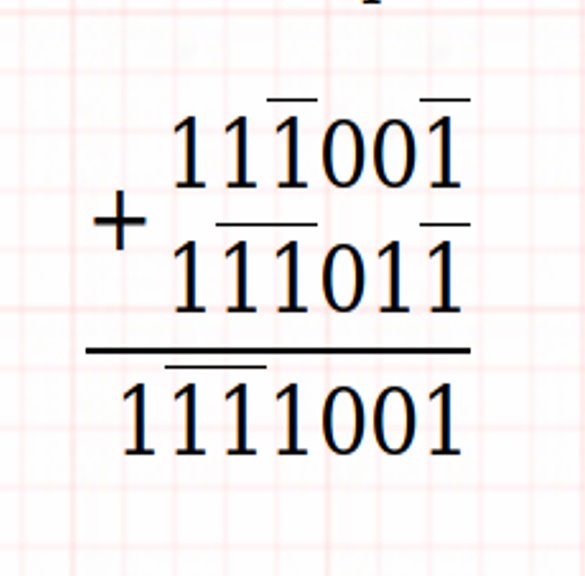
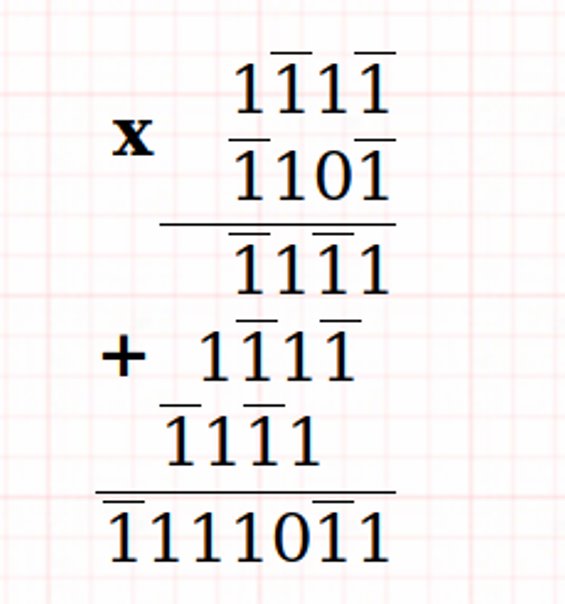
Circuitos combinacionais ternários (portões ternários)
Um circuito combinacional consiste em variáveis de entrada, portas lógicas ternárias e variáveis de saída. A saída do circuito depende apenas da entrada atual. As portas lógicas aceitam sinais das variáveis de entrada e geram sinais de saída. Esse processo transforma informações ternárias de
os dados de entrada fornecidos para os dados de saída ternários necessários.
Como mencionado acima, podemos facilmente nomear uma fração significativa dos operadores booleanos (não, e, ou, nand, nem, equivalência exclusiva ou, implicação); no entanto, não é razoável tentar nomear todos, exceto uma pequena fração do possível operadores ternários. Vamos considerar os seguintes circuitos ternários:
E (Mín) : É natural estender o Booleano e a função para uma função ternária, declarando que o resultado é verdadeiro apenas se ambas as entradas forem verdadeiras, falsas se alguma entrada for falsa e, caso contrário, desconhecidas.
E tabela de circuito / verdade Ou (Máx) : Também é natural estender o Booleano ou a função para ternário, declarando que o resultado é verdadeiro se alguma entrada for verdadeira, falsa apenas se ambas as entradas forem falsas e, caso contrário, desconhecida.
Ou tabela de circuito / verdade Consenso : Na lógica booleana, o inverso de exclusivo ou é verdadeiro quando as duas entradas são iguais e falso quando são diferentes. Existem várias extensões naturais dessa idéia para a lógica ternária. Uma delas é o consenso lógico de um conjunto de variáveis, que é verdadeiro se todas são verdadeiras, falsas se todas são falsas e, de outra forma, desconhecidas
Circuito de consenso / tabela verdade Qualquer um : Quando o consenso exigir que ambas as entradas concordem antes de afirmar qualquer coisa, exceto que desconhecida, o operador de aceitar qualquer coisa declara uma conclusão desconhecida apenas se ambas as entradas forem desconhecidas ou discordarem ativamente. Caso contrário, chega a uma conclusão a partir de qualquer entrada não desconhecida disponível.
Qualquer tabela de circuito / verdade Incremento e Decremento : Na lógica booleana, o inversor pode ser considerado como incrementador ou decrementador de seu módulo de argumento 2. Lógica interna, as funções de incremento e decremento do módulo 3 são bastante distintas da inversão.
Circuito de incremento e decréscimo Síntese, Minimização e Realização para Funções Ternárias
Relações inter-relacionadas no sistema lógico ternário
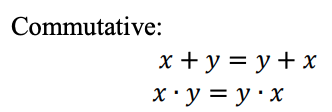
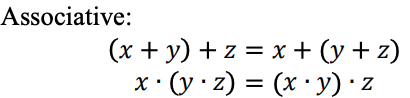
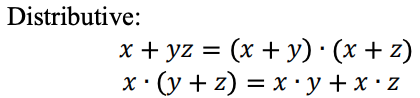
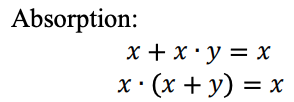
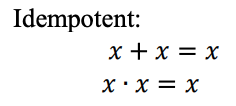
Uma função lógica ternária pode ser representada como uma expressão Max-Min. As expressões ternário Max-Min são definidas da seguinte maneira:
Variável : Qualquer símbolo que valorize o conjunto T ∈ {0,1,2} é uma variável ternária.
Literal : os literais são formas transformadas de uma variável. Eles são usados para formar expressões Max-Min.
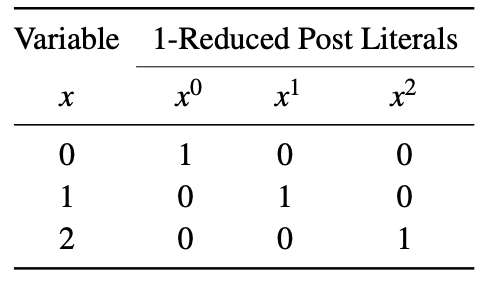
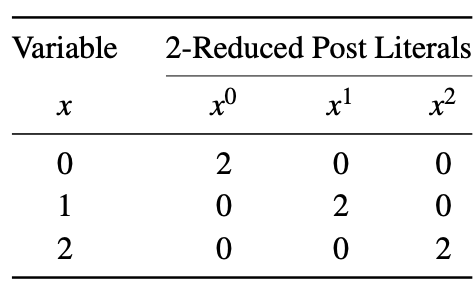
Na literatura, dois tipos de literais são comumente usados: pós literais reduzidos em 1 e pós literais reduzidos em 2. Um Post literal reduzido em 1 de uma variável x é representado como x i , onde i ∈ {0,1,2}. Quando x = i, então xi = 1, caso contrário xi = 0. Os literais pós reduzidos em 1 de uma variável são mostrados abaixo.
Um Post literal com redução de 2 de uma variável x é representado como x i , onde i ∈ {0,1,2}. Quando x = i, então xi = 2, caso contrário xi = 0. Os literais pós reduzidos em 2 de uma variável são mostrados abaixo. Este exemplo utiliza diferentes conjuntos de literais para formar expressões Max-Min, conforme discutido anteriormente.
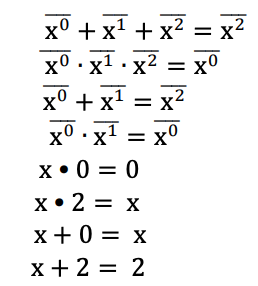
Minterm : Quando literais de variáveis de uma função são combinados usando a operação Min, o termo é chamado minterm. Por exemplo, para uma função lógica ternária de 3 variáveis F (x, y, z), xyz e xz são dois exemplos de mintermos.
Expressão de max e min : quando dois ou mais mintermos são combinados usando operações Max, a expressão é chamada de expressão de Max de minterms (Max-Min). Por exemplo, para uma função lógica ternária de 3 variáveis, F (x, y, z) = xy + yz + xyz é um exemplo de uma expressão Max-Min.
Qualquer função F (x, y, z) sempre pode ser representada como
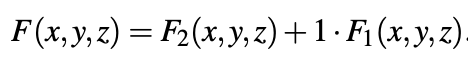
Três métodos básicos para minimizar as funções ternárias são:
- Manipulação da expressão da álgebra como na álgebra booleana.
- O método tabular.
- Método de mapa ternário K.
Para a implementação de circuitos ternários, é necessário converter a variável ternária em variável unária (usando a tabela Pós-literais com 2 reduções).
Meio adicionador ternário
Um circuito para a adição de dois números de 1 trit é referido como meio adicionador. o circuito não considera uma carga gerada na adição anterior. O processo de adição no sistema lógico ternário é mostrado abaixo. Aqui A e B são duas entradas e soma (S) e transporte (CARRY)
são duas saídas.
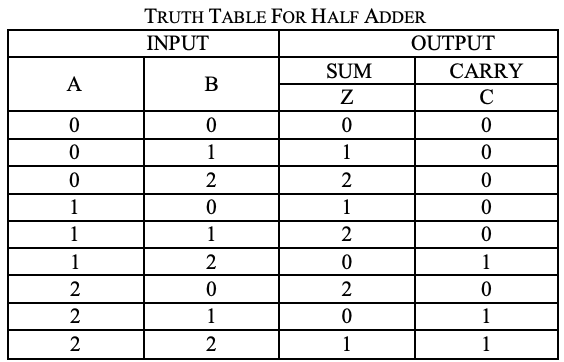
Análise
Um mapa de karnaugh (K-map) é usado para representar a soma e transportar a saída. Os mapas K são úteis para minimização e otimização de circuitos lógicos. Aqui é utilizado um mapa K de 2 entradas. Como nenhum agrupamento de 2 e 1 é possível, a equação de saída é a seguinte.
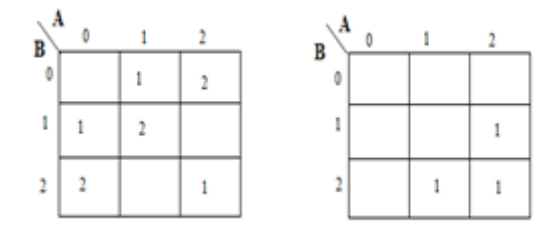
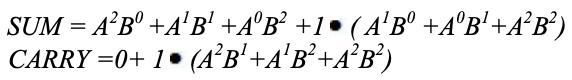
Implementação
Circuito ternário somador / verilogmodule half_adder ( input [1:0] A, [1:0] B, output [1:0] sum, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; wire [1:0] c0, c1, c2, c3; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a2,b0,i0); andgate and_2(a1,b1,i1); andgate and_3(a0,b2,i2); // partial products orgate or_1(i0, i1, o0); orgate or_2(o0, i2, o1); // f1 andgate and_4(a1,b0,i3); andgate and_5(a0,b1,i4); andgate and_6(a2,b2,i5); // partial products orgate or_3(i3, i4, o2); orgate or_4(o2, i5, o3); // f2 andgate and_7(o3,temp,o4); // 1.f2 andgate andc_0(a2,b1,c0); andgate andc_1(a1,b2,c1); orgate orc_0(c0,c1,c2); orgate orc_1(c2,i5,c3); andgate andc_2(c3,temp,carry); // carry orgate or_5(o1, o4, sum); // sum endmodule
Somador completo ternário
Como com os meio aditivos, um estágio de um somador completo ternário pode ser descrito por uma tabela numérica que fornece a soma SUM e executa CARRY como uma função das três entradas A, B, juntamente com o carry em C :
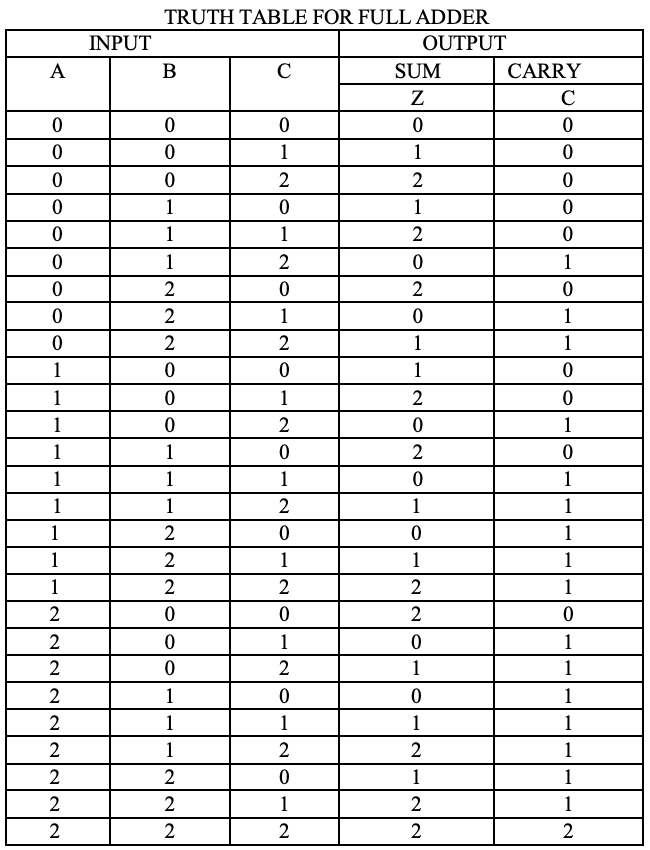
Análise
Um mapa de karnaugh (K-map) é usado para representar a soma e transportar a saída. Os mapas K são úteis para minimização e otimização de circuitos lógicos. Aqui é utilizado um mapa K de 3 entradas.
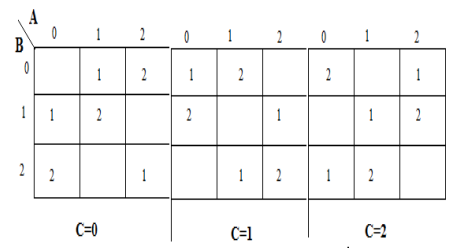
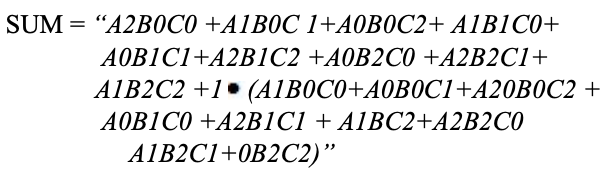
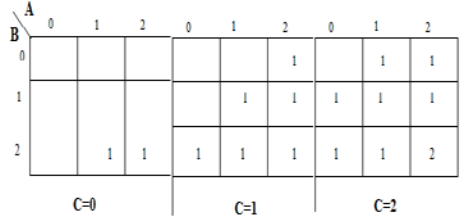
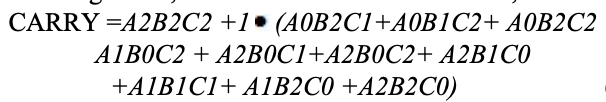
Implementação
Circuito somador ternário / verilog module ternary_full_adder ( input [1:0] A, [1:0] B, [1:0] c_in, output [1:0] sum, [1:0] c_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b00; wire [1:0] a0, a1, a2, b0, b1, b2, a20; wire [1:0] i0, i1, i2, i3, i4; wire [1:0] i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] o0, o1, o2, o3, o4, o5, o6, o7, o8, o9; wire [1:0] c0, c1, c2; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12, t13, t14, t15, t16; wire [1:0] g0, g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15; mask mk_1(A, a0, a1, a2); mask mk_2(B, b0, b1, b2); mask mk_3(c_in, c0, c1, c2); andgate3 and3_1(a2,b0,c0, i0); andgate3 and3_2(a1,b0,c1, i1); andgate3 and3_3(a0,b0,c2, i2); andgate3 and3_4(a1,b1,c0, i3); andgate3 and3_5(a0,b1,c1, i4); andgate3 and3_6(a2,b1,c2, i5); andgate3 and3_7(a0,b2,c0, i6); andgate3 and3_8(a2,b2,c1, i7); andgate3 and3_9(a1,b2,c2, i8); andgate3 and3_10(a1,b0,c0, i9); andgate3 and3_11(a0,b0,c1, i10); orgate or__(a2, a0, a20); andgate3 and3_12(a20,b0,c2, i11); // note a20 andgate3 and3_13(a0,b1,c0, i12); andgate3 and3_14(a2,b1,c1, i13); andgate3 and3_15(a1,B,c2, i14); andgate3 and3_16(a2,b2,c0, i15); andgate3 and3_17(a1,b2,c1, i16); andgate3 and3_18(temp2,b2,c2, i17); orgate or_1(i9, i10, o0); orgate or_2(o0, i11, o1); orgate or_3(o1, i12, o2); orgate or_4(o2, i13, o3); orgate or_5(o3, i14, o4); orgate or_6(o4, i15, o5); orgate or_7(o5, i16, o6); orgate or_8(o6, i17, o7); andgate and_1(o7, temp1, o8); // 1.f2 orgate or_9(i0, i1, h0); orgate or_10(h0, i2, h1); orgate or_11(h1, i3, h2); orgate or_12(h2, i4, h3); orgate or_13(h3, i5, h4); orgate or_14(h4, i6, h5); orgate or_15(h5, i7, h6); orgate or_16(h6, i8, h7); orgate or_17_(h7, o8, sum); // sum // carry andgate3 and3_19(a2,b2,c2, t0); // f1 andgate3 and3_20(a0,b1,c2, t1); andgate3 and3_21(a0,b2,c2, t2); andgate3 and3_22(a0,b2,c1, t3); andgate3 and3_23(a1,b2,c0, t4); andgate3 and3_24(a2,b2,c0, t5); andgate3 and3_25(a1,b1,c1, t6); andgate3 and3_26(a1,b2,c1, t7); andgate3 and3_27(a1,b0,c2, t8); andgate3 and3_28(a1,b1,c2, t9); andgate3 and3_29(a1,b2,c2, t10); andgate3 and3_25_(a2,b0,c2, t11); andgate3 and3_26_(a2,b1,c2, t12); andgate3 and3_27_(a2,b0,c1, t13); andgate3 and3_28_(a2,b1,c1, t14); andgate3 and3_29_(a2,b2,c1, t15); andgate3 and3_9_(a2,b1,c0, t16); orgate or_17(t1, t2, g0); orgate or_18(g0, t3, g1); orgate or_19(g1, t4, g2); orgate or_20(g2, t5, g3); orgate or_21(g3, t6, g4); orgate or_22(g4, t7, g5); orgate or_23(g5, t8, g6); orgate or_24(g6, t9, g7); orgate or_25(g7, t10, g8); orgate or_21_(g8, t11, g9); orgate or_22_(g9, t12, g10); orgate or_23_(g10, t13, g11); orgate or_24_(g11, t14, g12); orgate or_25_(g12, t15, g13); orgate or_5_(g13, t16, g14); //f2 andgate and_2(g14, temp1, g15); // 1.f2 orgate or_26(g15, t0, c_out); // carry endmodule
Subtrator completo ternário
O subtrator completo ternário é um circuito que subtrai duas entradas e empréstimos anteriores. A tabela de verdade para Subtractor é mostrada abaixo

Análise e Implementação do Subtrator Completo Ternário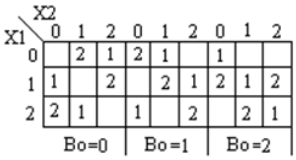
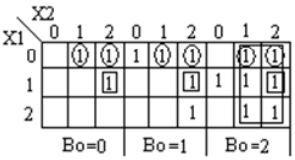
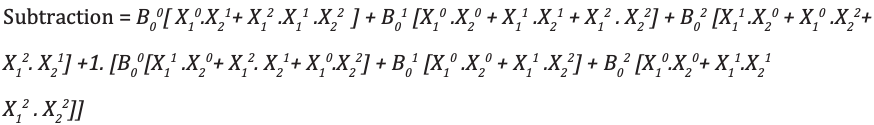
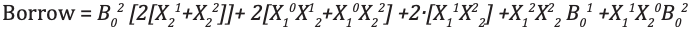
Código module full_subtractor( input [1:0] P, Q, b_in, output [1:0] diff, b_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b10; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] c0, c1, c2, c3; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7, h8, h9, h10, h11; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9; wire [1:0] p0, p1, p2; wire [1:0] q0, q1, q2; mask mk_1(P, p0, p1, p2); mask mk_2(Q, q0, q1, q2); mask mk_3(b_in, b0, b1, b2); andgate and_0(p0, q1, i0); andgate3 and3_0(p2, p1, q2, i1); orgate or_0(i0, i1, i2); andgate and_1(b0, i2, i3); // first expression andgate and_2(p0, q0, i4); andgate and_3(p1, q1, i5); andgate and_4(p2, q2, i6); orgate or_1(i4, i5, i7); orgate or_2(i7, i6, i8); andgate and_5(i8, b1, i9); // second expression andgate and_6(p1, q0, i10); andgate and_7(p0, q2, i11); andgate and_8(p2, q1, i12); orgate or_3(i10, i11, i13); orgate or_4(i13, i12, i14); andgate and_9(i14, b2, i15); // third expression orgate or_5(i3, i9, i16); orgate or_6(i16, i15, c0); //f1 orgate or_7(i10, i12, t0); orgate or_8(t0, i11, t1); andgate and_10(t1, b0, t2); // 1 expression andgate and_11(p1, q2, i17); orgate or_9(i4, i17, t3); andgate and_12(t3, b1, t4); // 1- expression orgate or_10(i4, i5, t5); orgate or_11(t5, i6, t6); andgate and_12_(t6, b2, t7); // 1-- expression orgate or_12(t2, t4, t8); orgate or_13(t8, t7, t9); andgate and_13(t9, temp1, c1); orgate or_14(c0, c1, diff); // difference orgate or_15(q1, q2, h0); andgate and_14(h0, temp2, h1); andgate and_15(h1, b2, h3); // 1 b orgate or_16(i0, i11, h4); andgate and_16(h4, temp2, h5); // 1- b andgate and_17(i17, temp2, h6); // 1-- b andgate3 and3_1(p2, q2, b1, h7); // 1--- b andgate3 and3_2(p1, q0, b2, h8); // 1---- b orgate or_17(h3, h5, h9); orgate or_18(h9, h6, h10); orgate or_19(h10, h7, h11); orgate or_20(h11, h8, b_out); // borrow endmodule
Ondulador ternário transportador somador
O RCA (Ripple-carry Adder) é um circuito bem conhecido para realizar a adição de dois números por somadores ternários completos em cascata. Um RCA ternário é bastante semelhante ao seu equivalente binário. Um meio somador ternário é empregado para adicionar os dígitos ternários menos significativos. O restante é resumido por Ternary Full Adders. Como mencionado anteriormente, o Ternary Full Adder adiciona três variáveis de entrada ternárias.
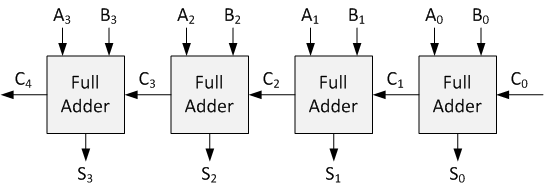
Implementação
código verilog: ondulação ternária module ternary_ripple_adder ( input [15:0] input1 , input [15:0] input2 , output [15:0] out , output [1:0] overflow_trit ); wire [15:0] carry ; reg tem; assign carry[0] = tem; assign carry[1] = tem; always @(input1, input2) begin tem <= 1'b0; end generate genvar i; for (i = 0; i <= 12; i=i+2) begin full_add af({input1[i+1],input1[i]}, {input2[i+1],input2[i]}, {carry[i+1],carry[i]}, {out[i+1], out[i]}, {carry[i+3],carry[i+2]}); end full_add af({input1[15],input1[14]}, {input2[15],input2[14]}, {carry[15],carry[14]}, {out[15], out[14]}, overflow_trit); endgenerate endmodule
Comparadores ternários
O circuito comparador ternário acampa duas entradas X 1 , X 2 e, consequentemente, gera a saída como X 1 = X 2 , X 1 > X 2 , X 1 <X 2 . A tabela de verdade para um comparador ternário é mostrada abaixo
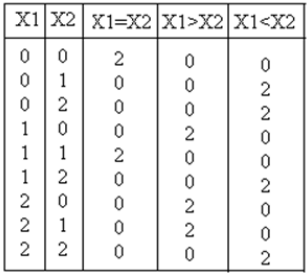
Análise e implementaçãoA equação de saída para X 1 = X 2 , X 1 > X 2 , X 1 <X 2 é:
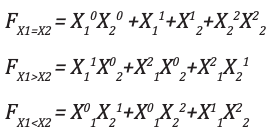
Os mapas k correspondentes são mostrados abaixo

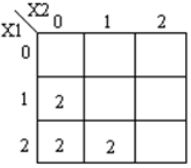
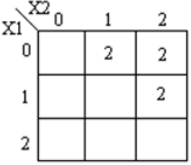
Código module ternary_comparators ( input [1:0] x1, x2, output [1:0] f1, f2, f3 ); wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7; wire [1:0] h0, h1, h2, h3, h4, h5; wire [1:0] x10, x11, x12; wire [1:0] x20, x21, x22; mask mk_1(x1, x10, x11, x12); mask mk_2(x2, x20, x21, x22); andgate and_0(x10, x20, t0); andgate and_1(x22, x22, t1); orgate or_0(t0, t1, h0); orgate or_1(h0, x11, h1); orgate or_2(h1, x21, f1); // x1 == x2 andgate and_2(x11, x20, t2); andgate and_3(x12, x20, t3); andgate and_4(x12, x21, t4); orgate or_3(t2, t3, h3); orgate or_4(h3, t4, f2); // x1>x2 andgate and_5(x10, x21, t5); andgate and_6(x10, x22, t6); andgate and_7(x11, x22, t7); orgate or_5(t5, t6, h4); orgate or_6(h4, t7, f3); // x1<X2 endmodule
Multiplicador ternário
O multiplicador ternário é um circuito que multiplica dois números de entrada e gera o produto correspondente. A tabela de verdade para este circuito é mostrada abaixo:
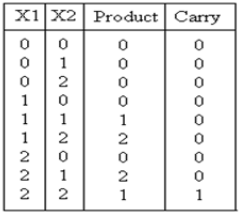
Análise e implementaçãoA expressão resultante para o produto e o transporte são mostrados:
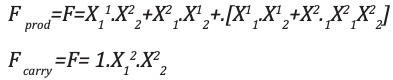
Os mapas K correspondentes são mostrados:
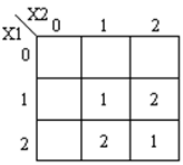
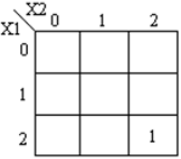
Código module ternary_multiplier ( input [1:0] A, [1:0] B, output [1:0] product, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a1,b2,i0); andgate and_2(a2,b1,i1); orgate or_1(i0, i1, o0); // f1 andgate and_4(a1,b1,i3); andgate and_5(a2,b2,i4); orgate or_3(i3, i4, o2); andgate and_3(temp,o2,o3); orgate or_4(o3, o0, product); // product andgate andc_0(a2,b2,o4); andgate andc_1(temp,o4,carry); // carry endmodule
Multiplexadores e desmultiplexadores ternários
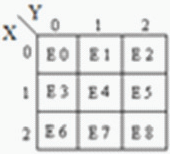
Multiplexador é um circuito com várias entradas e uma única saída. Também é conhecido como decodificador. A função de saída do multiplexador é determinada pelo número de linhas de função. Assim, para 2 trit
multiplexador, a saída será 3 2 = 9 e duas serão as linhas de seleção da função. Multiplexador ou seja, função
A lógica de seleção seleciona 1 de 9 funções como saída. A lógica de seleção de função é implementada usando portas lógicas. A equação de saída da lógica de seleção de função é:
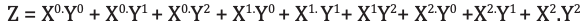
Análise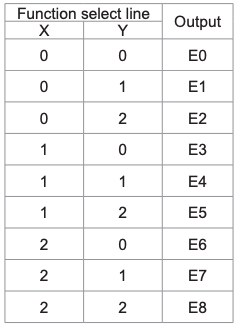
O desmultiplexador também é conhecido como codificador. Sua funcionalidade é inversa à do multiplexador. Ele aceita a entrada única e a distribui por várias saídas
Trava ternária simples
Embora o projeto de circuitos que implementam lógica ternária combinatória seja direto, o projeto de um elemento de memória ternária simples e robusto (por exemplo, trava) adequado para a implementação de circuitos integrados (IC) tem sido desafiador. No entanto, uma trava ternária simples pode ser obtida substituindo as portas binárias NOR ou NAND usadas pelas correspondentes portas ternárias T_NOR ou T_NAND.
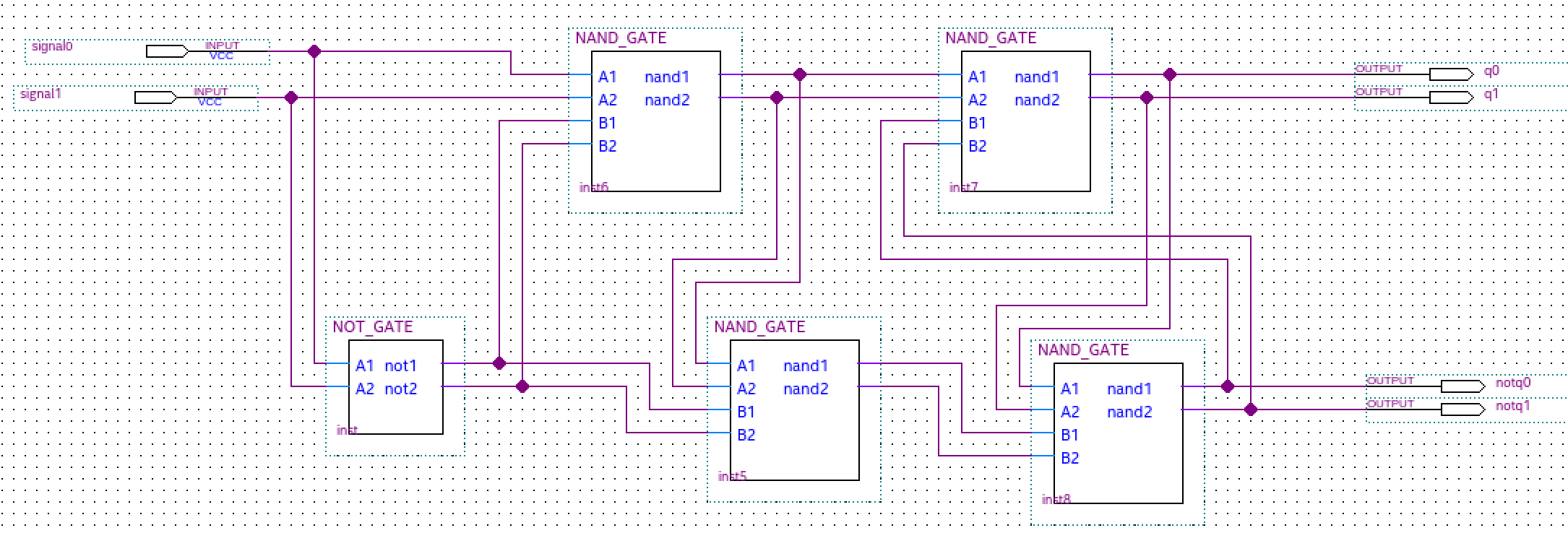
Flip-flap-flop simples de Ternário D
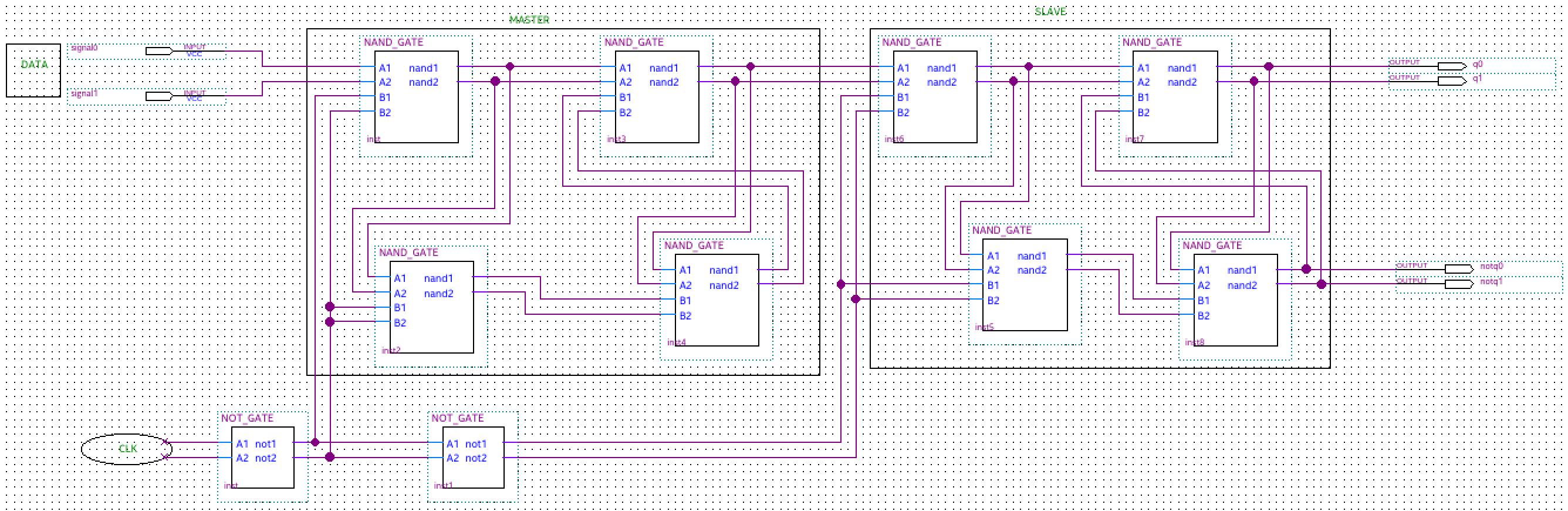
O flip-flop ternário D do escravo mestre (MS) D é realizado com base nos trincos D ternários. Isso é semelhante à maneira como o flip-flop binário D (FF) é realizado usando trincos D binários. O diagrama lógico e a descrição da operação do flip-flop binário D da MS são bem conhecidos. Para implementar o MS ternário D FFF , substituímos as travas D binárias pelas travas D ternárias (realizadas com as portas mínimas negadas ternárias de duas entradas - NAND) e os inversores binários por inversores ternários simples (STI). As tabelas verdadeiras para os circuitos NAND ternários e STI ternários são mostradas
Tabela da verdade para circuitos nand e sti Para MS ternário D FFF com relógio binário, os dados são ternários (lógica 0, 1 e 2) e o relógio é binário (baixo e alto - em nosso
implementação, lógica 0 e 2). O MS ternário D FFF com
relógio binário pode ler os dados quando o relógio passa de baixo para
alto (margem positiva) ou de alto a baixo (margem negativa), dependendo
no número de ISTs.
As entradas do D FFF ternário são Data e Clk, e as saídas são Q e Not_Q. O sinal do relógio é binário e os níveis lógicos são denotados 0 e 2, a fim de manter a correspondência com a implementação elétrica
Unidade aritmética e lógica ternária de 1 bit (T-ALU)
A Unidade Lógica Aritmética Ternária (ALU) é um circuito digital usado para executar operações aritméticas e lógicas. Ele representa o bloco de construção fundamental da Unidade Central de Processamento (CPU) de um computador ternário. A ALU realiza operações aritméticas, como operações de adição, subtração, multiplicação e lógica, comparando NAND, NOR, NOT, AND e OR. Abaixo é mostrada uma arquitetura primitiva de uma ULA de 1 trit
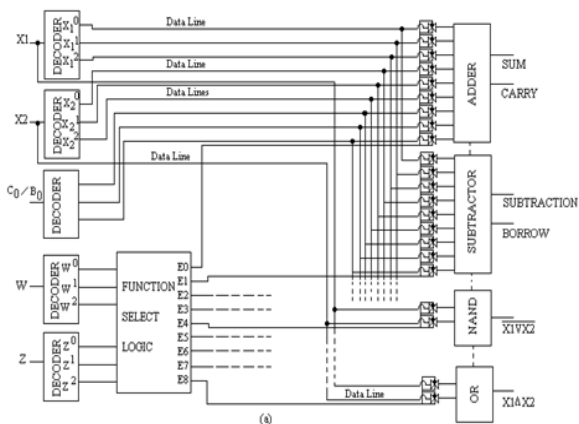
Tabela da verdade e funcionando para T-ALU Os componentes básicos da ALU são decodificadores, lógica de seleção de função (Multiplexador), porta de transmissão e módulos de processamento separados. A lógica de seleção de função seleciona 1 de 9 funções listadas, dependendo do estado lógico nas linhas de seleção de função W e Z.
As linhas de saída da lógica de seleção são conectadas ao TG (gate ternário) associado a cada módulo. Qualquer módulo é selecionado apenas quando o TG associado está ativado, caso contrário, é isolado das linhas de dados. Por exemplo, se a entrada das linhas de seleção W e Z = 0, a saída E 0 da lógica de seleção é alta (2), enquanto E 1 a E 8 é baixa (0), portanto, o TG associado ao módulo adicionador será ativado, permitindo que os dados
linhas a serem conectadas aos módulos somadores, enquanto outros módulos são isolados das linhas de dados.
Finalmente, em cascata n / 2 trit ALU fatias, um n trit ALU pode ser formado.