As classificações de mesclagem funcionam de acordo com este princípio:

1. As sub-matrizes ordenadas são pesquisadas (como uma opção - são formadas).
2. Subarrays ordenados são concatenados em um subarray ordenado comum.

Por si só, qualquer sub-matriz ordenada dentro da matriz não tem muito valor. Mas se em uma matriz encontramos dois sub-arranjos ordenados, então isso é uma questão completamente diferente. O fato é que você pode mesclá-los muito rapidamente e a um custo mínimo - para formar uma sub-matriz geral ordenada a partir de um par de sub-estruturas ordenadas.



Como você pode ver, combinar duas matrizes ordenadas em uma não é fácil, mas muito simples. Você precisa mover simultaneamente nas duas matrizes da esquerda para a direita e comparar os próximos pares de elementos das duas matrizes. O elemento menor é enviado para a caldeira comum. Quando os elementos terminam em uma das matrizes, os elementos restantes da outra matriz são simplesmente transferidos para a lista principal em ordem.

Este é o sal dos algoritmos desta classe. Inicialmente, uma matriz aleatória pode ser dividida em várias sub-matrizes ordenadas pequenas. Na mesclagem em pares, o número de sub-matrizes ordenadas diminui, o comprimento de cada uma delas aumenta. Na última etapa, a matriz consiste em apenas duas sub-matrizes ordenadas que se fundem em uma única estrutura ordenada.


O autor deste conceito é John von Neumann. Às vezes, há uma alegação controversa de que ele inventou a classificação enquanto trabalhava no projeto de Manhattan, uma vez que se deparou com a tarefa de fornecer cálculos eficazes de uma enorme quantidade de dados estatísticos no desenvolvimento de uma bomba nuclear. É difícil avaliar a credibilidade dessa versão, pois seu primeiro trabalho de classificação por fusão remonta a 1948, e a criação da bomba foi concluída três anos antes. No entanto, que tipo de classificação atômica existe, vamos dar uma olhada.

Fusão Natural Neumann

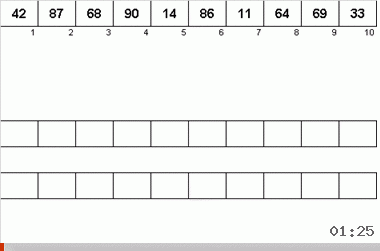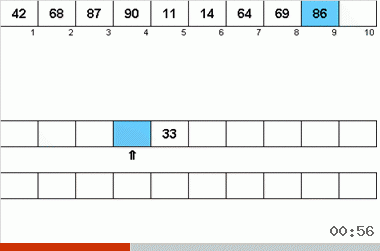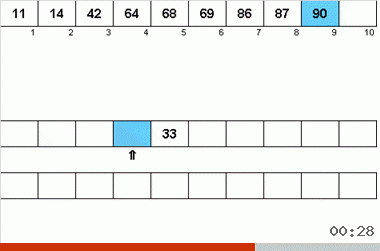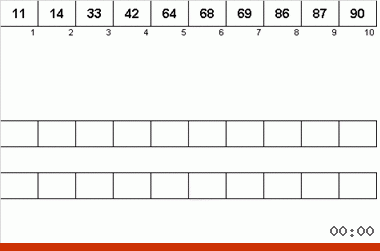
O algoritmo Neyman foi influenciado pelos recursos de design dos computadores dos anos 40. Parecia assim:

1. No total, são utilizadas três fitas magnéticas - a principal, na qual são gravados dados não classificados e dois dados auxiliares.
2. Os dados são lidos sequencialmente na fita principal.
3. Embora os dados lidos sequencialmente sejam uma sub-matriz ordenada, eles são copiados para uma das fitas auxiliares.
4. Assim que o próximo subarray classificado for concluído (ou seja, um elemento menor que o anterior for encontrado na fita principal), um ponteiro será colocado na fita auxiliar (final da subarray) e a troca para outra fita auxiliar ocorrerá.
5. Os pontos 2 a 4 são repetidos novamente, apenas os dados são transferidos para outra fita auxiliar. No final do próximo subarray ordenado, a fita principal alterna alternadamente para uma fita auxiliar e depois para outra.
6. Quando todos os dados da fita principal tiverem sido lidos, o processamento das fitas auxiliares ocorrerá.
7. As duas fitas auxiliares leem os dados por sua vez.
8. Nesse caso, os próximos dados de duas fitas são comparados entre si. De acordo com os resultados da comparação, o menor elemento do par é registrado na fita principal.
9. Como os limites das matrizes nas fitas auxiliares são marcados com ponteiros, a leitura e a comparação ocorrem apenas nas sub-matrizes ordenadas.
10. Se em uma das fitas auxiliares os elementos do próximo sub-arranjo terminarem, a partir da fita restante, o restante do sub-arranjo será simplesmente transferido para a fita principal.
11. Repetimos todo o processo novamente até que os dados na fita principal sejam uma matriz totalmente ordenada.

A classificação de Neumann é um algoritmo adaptável: não apenas corrige as partes classificadas da matriz, mas também tenta, primeiro de tudo, aumentá-las, de modo que, com base em subarrays ordenados alongados, forme sub-arrays ainda mais longos. Portanto, também é chamado de classificação de mesclagem adaptativa .

A complexidade desse algoritmo é modesta - O ( n ² ) e, no entanto, para os pioneiros da computação em tubos, essa foi uma inovação.

No exemplo dessa primeira classificação de mesclagem, uma desvantagem dessa classe de algoritmos já é visível - o custo da memória adicional. Nesse sentido, quase todas as classificações de mesclagem exigem adicionalmente O ( n ), no entanto, exceções elegantes são raras.

Fusão direta Bowes-Nelson

A rigor, o algoritmo Bowes-Nelson é uma rede de classificação, não uma classificação. No processo, a matriz e todas as suas sub-matrizes são divididas ao meio e nada impede que todas essas metades sejam processadas em paralelo em todos os estágios. No entanto, também pode ser representado na forma de classificação. E também abordaremos o tópico de classificação de redes.

1. A matriz é dividida ao meio - nas metades esquerda e direita.
2. Os elementos são divididos em grupos.
3. Na primeira iteração, esses são os dois elementos (o 1º elemento da metade esquerda + o 1º elemento da metade direita, o 2º elemento da metade esquerda + o 2º elemento da metade direita, etc.), na segunda iteração - os quatro elementos (1- 2º e 2º elementos da metade esquerda + 1º e 2º elementos da metade direita, 3º e 4º elementos da metade esquerda + 3º e 4º elementos da metade direita, etc.), no terceiro - oito, etc.
4. Os elementos de cada grupo da metade esquerda são classificados em sub-matrizes, os elementos de cada grupo da metade direita também são classificados em sub-vetores.
5. Mesclar as sub-matrizes ordenadas do parágrafo anterior.
6. Voltamos ao ponto 1. O ciclo continua até que os tamanhos dos grupos sejam menores que o tamanho da matriz.

Pode parecer que seja necessária memória adicional aqui. Mas não! Para uma percepção mais compreensível da animação, as metades esquerda e direita da matriz estão localizadas uma na outra, de modo que a posição relativa das sub-matrizes comparadas é mais óbvia. No entanto, devido à bissecção estrita, é possível um algoritmo no qual todas as comparações e trocas são feitas, sem envolver recursos adicionais da memória. O que é muito incomum para a classificação de mesclagem.

def bose_nelson(data): m = 1 while m < len(data): j = 0 while j + m < len(data): bose_nelson_merge(j, m, m) j = j + m + m m = m + m return data def bose_nelson_merge(j, r, m): if j + r < len(data): if m == 1: if data[j] > data[j + r]: data[j], data[j + r] = data[j + r], data[j] else: m = m // 2 bose_nelson_merge(j, r, m) if j + r + m < len(data): bose_nelson_merge(j + m, r, m) bose_nelson_merge(j + m, r - m, m) return data 

Há algo em todas as fusões de classificação que as tornam semelhantes à bomba de hidrogênio. Primeira divisão ocorre, depois síntese.

Referências

Mesclar / Mesclar

Artigos da série:

• Aplicativo Excel AlgoLab.xlsm
• Classificações de Câmbio
• Classificações de inserção
• Classificar por seleção
• Mesclar classificações
  • Fusão equilibrada de cima para baixo e de baixo para cima
  • Classificação de mesclagem multifásica
  • Classificação de mesclagem em cascata
  • Classificação de mesclagem oscilante
  • Classificações roscadas e imiscíveis
  • Comparação de Mesclagem
• Classificar por distribuição
• Classificação híbrida

Agora, as duas classificações mencionadas no artigo de hoje estão disponíveis no aplicativo AlgoLab (para quem estuda algoritmos usando esse aplicativo do Excel, atualize o arquivo). E em apenas alguns dias, com o lançamento de uma próxima sequela por ordem de mesclagem, vários outros algoritmos dessa classe estarão disponíveis.

Há uma restrição para a classificação de Bowes-Nelson - o tamanho da matriz deve ser uma potência de duas. Se essa condição não for atendida, a macro cortará a matriz em um tamanho adequado.

Este artigo foi escrito com o apoio da EDISON Software, uma empresa que cria software de reconstrução 3D e está desenvolvendo sofisticados equipamentos de medição .