Após o verdadeiro boom de jogos de tabuleiro do final dos anos 2000, a família deixou várias caixas com jogos. Um deles é o jogo "Hare and Hedgehog" na versão original em alemão. Um jogo para vários jogadores, no qual o elemento aleatório é minimizado, e o cálculo sóbrio e a capacidade do jogador de "olhar para frente" em vários passos vencem.
Minhas derrotas frequentes no jogo me levaram a escrever "inteligência" de computador para escolher a melhor jogada. Inteligência, idealmente capaz de combater o grande mestre de Hare e Hedgehog (e o que, chá, não xadrez, o jogo será mais fácil). O restante do artigo descreve o processo de desenvolvimento, a lógica da IA e um link para a fonte.
Regras do jogo Hare and Hedgehog
No campo de jogo de 65 células, existem várias fichas de jogador, de 2 a 6 participantes (meu desenho, não canônico, parece, é claro, mais ou menos):
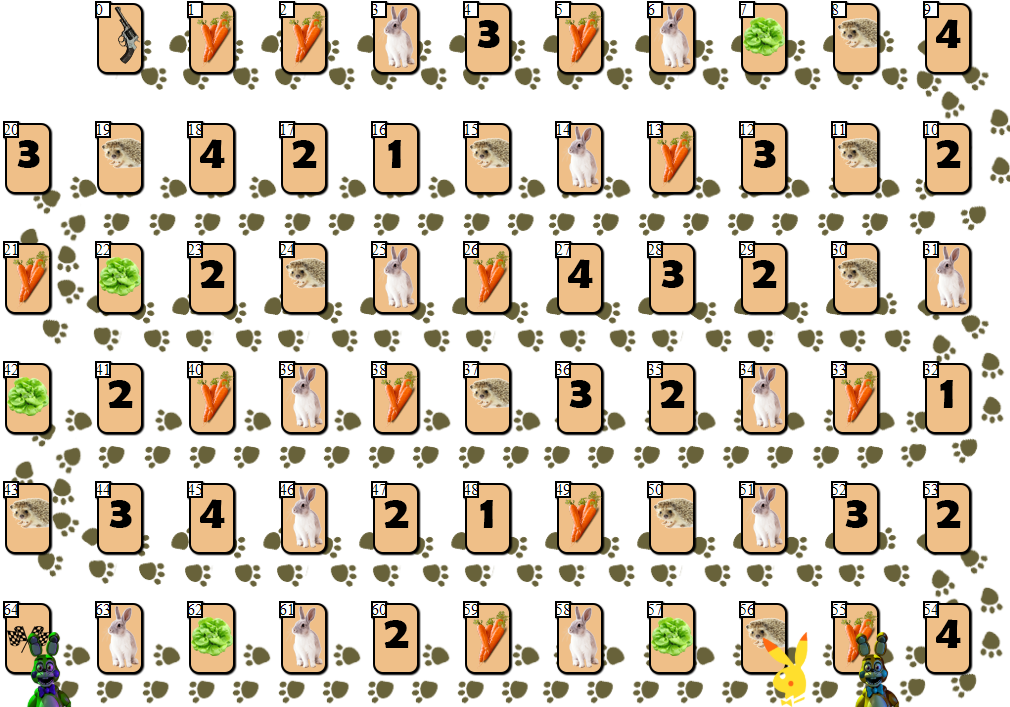
Além das células com índices 0 (início) e 64 (término), apenas um jogador pode ser colocado em cada uma das células. O objetivo de cada jogador é avançar para a célula de chegada, à frente dos rivais.
O "combustível" para avançar é a cenoura - a "
moeda " do jogo. No início, cada jogador recebe 68 cenouras, que ele dá (e às vezes recebe) enquanto se move.
Além das cenouras, no início o jogador recebe 3 cartas de salada. Salada é um "artefato" especial do qual um jogador deve
se livrar antes do final. Livrar-se de alface (e isso só pode ser feito em uma gaiola especial de alface, assim:

), o jogador, inclusive, recebe cenouras adicionais. Antes disso, pule sua jogada. Quanto mais jogadores na frente da salada deixarem o cartão, mais cenouras esse jogador receberá: 10 x (posição do jogador no campo em relação a outros jogadores). Ou seja, o jogador em pé no segundo campo receberá 20 cenouras, deixando a gaiola da salada.
Células com números 1 - 4 podem trazer várias dezenas de cenouras se a posição do jogador coincidir com o número na célula (1 - 4, a célula com número 1 também é adequada para as 4ª e 6ª posições no campo), por analogia com a célula de alface.
O jogador pode pular a jogada, permanecendo na gaiola com a imagem de cenouras e receber ou dar 10 cenouras para esta ação. Por que um jogador deveria dar "combustível"? O fato é que um jogador pode terminar com apenas 10 cenouras após o lance final (20 se você terminar em segundo, 30 se terminar em terceiro, etc.).
Finalmente, o jogador pode obter 10 x N cenouras dando N passos no ouriço
livre mais próximo (se o ouriço mais próximo estiver ocupado, tal movimento é impossível).
O custo do avanço é calculado não proporcionalmente ao número de movimentos, de acordo com a fórmula (com arredondamentos para cima):
,
onde N é o número de etapas a seguir.
Então, para avançar uma célula, o jogador dá 1 cenoura, 3 cenouras para 2 células, 6 cenouras para 3 células, 10 para 4, ..., 210 cenouras para mover 20 células para frente.
A última célula - a célula com a imagem de uma lebre - introduz um elemento aleatório no jogo. Tendo ficado em uma jaula com uma lebre, o jogador tira uma carta especial da pilha, após a qual alguma ação é realizada. Dependendo da carta e da situação do jogo, o jogador pode perder algumas cenouras, obter cenouras extras ou pular um turno. Vale ressaltar que entre as cartas com “efeitos” existem vários cenários negativos para o jogador, o que incentiva o jogo a ser cuidadoso e calculado.
Implementação sem IA
Na primeira implementação, que se tornará a base para o desenvolvimento do "intelecto" do jogo, me limitei à opção pela qual cada jogador faz um movimento - uma pessoa.
Decidi implementar o jogo como cliente - um site estático de uma página, cuja “lógica” é implementada no JS e no servidor - o aplicativo da API WEB. O servidor está escrito no .NET Core 2.1 e produz um artefato de montagem - um arquivo dll, que pode ser executado no Windows / Linux / Mac OS.
A “lógica” da parte do cliente é minimizada (assim como o UX, pois a GUI é puramente utilitária). Por exemplo, o Web client não realiza a verificação para verificar se as regras solicitadas pelo player são aceitáveis. Essa verificação é realizada no servidor. O servidor informa ao cliente o que o jogador pode fazer a partir da posição atual do jogo.
O servidor é uma
máquina clássica de
Moore . A lógica do servidor não possui conceitos como "cliente conectado", "sessão de jogo" etc.
Tudo o que o servidor faz é processar o comando recebido (HTTP POST). O
padrão de "comando" é implementado no servidor. O cliente pode solicitar a execução de um dos seguintes comandos:
- iniciar um novo jogo, ou seja, "Coloque" fichas do número especificado de jogadores em um tabuleiro "limpo"
- faça o movimento indicado no comando
Para a segunda equipe, o cliente envia ao servidor a posição atual do jogo (objeto da classe Disposition), ou seja, uma descrição da seguinte forma:
- posição, número de cenouras e alface para cada lebre, além de um campo booleano adicional indicando que a lebre está perdendo sua vez
- índice da lebre fazendo a jogada.
O servidor não precisa enviar informações adicionais - por exemplo, informações sobre o campo de jogo. Assim como para gravar um desenho de xadrez, não é necessário pintar o arranjo de células em preto e branco no quadro - essas informações são consideradas constantes.
Em resposta, o servidor indica se o comando foi concluído com êxito. Tecnicamente, um cliente pode, por exemplo, solicitar uma movimentação inválida. Ou tente criar um novo jogo para um único participante, o que obviamente não faz sentido.
Se a equipe for bem-sucedida, a resposta conterá uma nova
posição no jogo, bem como uma lista de jogadas que podem ser feitas pelo próximo jogador na fila (atual para a nova posição).
Além disso, a resposta do servidor contém alguns campos de serviço. Por exemplo, o texto de uma carta de uma lebre é "puxado" por um jogador em uma etapa na gaiola correspondente.
Turno do jogador
A vez do jogador é codificada como um número inteiro:
- 0, se o jogador for forçado a permanecer na célula atual,
1, 2, ... N para 1, ... N dá um passo à frente, - -1, -2, ... -M para mover as células 1 ... M de volta para o ouriço livre mais próximo,
- 1001, 1002 - códigos especiais para o jogador que decidiu ficar na célula de cenoura e receber (1001) ou dar (1002) 10 cenouras para isso.
Implementação de software
O servidor recebe o JSON do comando solicitado, o analisa em uma das classes de solicitação correspondentes e executa a ação solicitada.
Se o cliente (jogador) solicitou uma mudança com o código CMD da posição (POS) transferida para a equipe, o servidor executou as seguintes ações:
- verifica se tal movimento é possível
- cria uma nova posição a partir da atual, aplicando as modificações correspondentes,
recebe muitos movimentos possíveis para uma nova posição. Deixe-me lembrá-lo de que o índice do jogador que está fazendo a jogada já está incluído no objeto que descreve a posição , - retorna ao cliente uma resposta com uma nova posição, possíveis movimentos ou o sinalizador de sucesso igual a falso e uma descrição do erro.
A lógica de verificar a admissibilidade do movimento solicitado (CMD) e construir uma nova posição acabou por estar um pouco mais próxima do que gostaríamos. Com essa lógica, o método de encontrar movimentos aceitáveis tem algo em comum. Toda essa funcionalidade é implementada pela classe TurnChecker.
Na entrada dos métodos de verificação / execução, o TurnChecker recebe um objeto da classe da posição do jogo (Disposição). O objeto Disposition contém uma matriz com dados do jogador (Haze [] haze), o índice do jogador que faz a jogada + algumas informações de serviço preenchidas durante a operação do objeto TurnChecker.
O campo de jogo descreve a classe FieldMap, que é implementada como um
singleton . A classe contém uma matriz de células + algumas informações gerais usadas para simplificar / acelerar os cálculos subseqüentes.
Considerações de desempenhoNa implementação da classe TurnChecker, tentei evitar loops o máximo possível. O fato é que os métodos para obter o conjunto de movimentos permitidos / execução de um movimento serão posteriormente chamados milhares (dezenas de milhares) de vezes durante o procedimento de busca de um movimento quase ideal.
Assim, por exemplo, calculo quantas células um jogador pode avançar com N cenouras, usando a fórmula:
return ((int)Math.Pow(8 * N + 1, 0.5) - 1) / 2;
Verificando se a célula i está ocupada por um dos jogadores, não analiso a lista de jogadores (já que essa ação provavelmente terá que ser executada várias vezes), mas
recorro o dicionário do formulário preenchido antecipadamente com o formulário
[cell_index, busy_cage_ flag] .
Ao verificar se a célula de ouriço especificada é a mais próxima (atrás) da célula atual ocupada pelo jogador, também comparo a posição solicitada com um valor de um dicionário do formato
[cell_index, closest_back_dezh] _index] - informações estáticas.
Implementação com IA
Um comando é adicionado à lista de comandos processados pelo servidor: execute uma movimentação quase ideal selecionada pelo programa. Essa equipe é uma pequena modificação do comando "movimento do jogador", do qual, de fato, o campo de movimento (
CMD ) foi removido.
A primeira decisão que vem à mente é usar heurísticas para selecionar a melhor opção possível. Por analogia com o xadrez, podemos avaliar cada uma das posições de jogo obtidas com a nossa jogada, definindo algum tipo de classificação para essa posição.
Avaliação da posição heurística
Por exemplo, no xadrez, fazer uma avaliação (sem se arrastar para a selva das aberturas) é bastante simples: no mínimo, você pode calcular o "custo" total das peças, levando o valor do cavaleiro / bispo para 3 peões, o valor de uma torre para 5 peões, a rainha para 9 e o rei para
int Peões
.MaxValue . É fácil melhorar a estimativa, por exemplo, adicionando-a (com um fator de correção - fator / expoente ou outra função):
- o número de movimentos possíveis da posição atual,
- proporção de ameaças para figuras inimigas / ameaças do inimigo.
É feita uma avaliação especial da posição do tapete:
int.MaxValue , se o xeque-mate colocar o computador,
int.MinValue se o xeque-mate colocar a pessoa.
Se você solicitar que o processador de xadrez escolha a próxima jogada, guiado apenas por essa avaliação, o processador provavelmente escolherá não as piores. Em particular:
- Não perca a oportunidade de pegar um pedaço maior ou xeque-mate,
- provavelmente, ele não conduzirá os números pelos cantos,
- Ele não coloca o número sob ataque novamente (dado o número de ameaças na avaliação).
Naturalmente, tais movimentos do computador não lhe darão uma chance de sucesso com um oponente que faz seus movimentos no menor sentido. O computador ignorará qualquer um dos plugues. Além disso, ele provavelmente não hesita em trocar a rainha por um peão.
No entanto, o algoritmo para avaliação heurística da atual posição de jogo no xadrez (sem reivindicar os louros do programa campeão) é bastante transparente. Você não pode dizer sobre o jogo Hare and Hedgehog.
No caso geral, no jogo Hare e Hedgehog, uma máxima um tanto embaçada funciona: “
é melhor ir além com mais cenouras e menos alface ”. No entanto, nem tudo é tão simples. Digamos, se um jogador tiver 1 carta de salada no meio do jogo, essa opção pode ser bastante boa. Mas o jogador que está na linha de chegada com uma carta de salada obviamente estará em uma situação perdida. Além do algoritmo de avaliação, eu também gostaria de "dar uma espiada" um passo além, assim como as ameaças às peças podem ser contadas em uma avaliação heurística de uma posição no xadrez. Por exemplo, vale a pena considerar o bônus de cenoura recebido por um jogador que sai da célula de alface / célula de posição (1 ... 4), levando em consideração o número de jogadores à frente.
Deduzi a nota final como uma função:
E = Ks * S + Kc * C + Kp * P,
onde S, C, P são notas calculadas usando cartões de salada (S) e cenouras © nas mãos do jogador, P são as notas dadas ao jogador pela distância percorrida.
Ks, Kc, Kp são os fatores de correção correspondentes (serão discutidos mais adiante).
A maneira mais fácil é determinar a marca
do caminho percorrido :
P = i * 3, onde i é o índice da célula na qual o player está localizado.
A classificação C (cenoura) já é mais difícil.
Para obter um valor C específico, escolho uma das 3 funções
de um argumento (o número de cenouras nas mãos). O índice da função C ([0, 1, 2]) é determinado pela posição relativa do jogador no campo de jogo:
- [0] se o jogador tiver completado menos da metade do campo de jogo,
- [2] se um jogador tiver cenouras suficientes (mb, até abundantes) para terminar,
- [1] em outros casos.
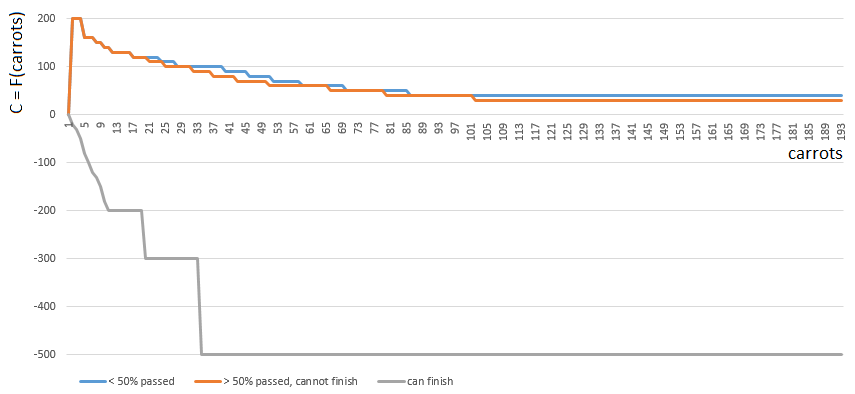
As funções 0 e 1 são semelhantes: o "valor" de cada cenoura nas mãos do jogador diminui gradualmente com o aumento do número de cenouras nas mãos. O jogo raramente incentiva os Plyushkins. No caso 1 (metade do campo passou), o valor das cenouras diminui um pouco mais rápido.
A função 2 (o jogador pode terminar), pelo contrário, impõe uma multa grande (valor do coeficiente negativo) a cada cenoura nas mãos do jogador - quanto mais cenouras, maior o coeficiente de penalidade. Como com um excesso de cenouras, o acabamento é proibido pelas regras do jogo.
Antes de calcular a quantidade de cenouras nas mãos do jogador, é especificado levando em consideração as cenouras por movimento da célula de alface / célula número 1 ... 4.
Uma classe de “
alface ” S é deduzida de maneira semelhante. Dependendo da quantidade de salada nas mãos do jogador (0 ... 3), uma função é selecionada
ou
. Argumento de função
. - novamente, o caminho "relativo" percorrido pelo jogador. Ou seja, o número de células com salada restante na frente (em relação à célula ocupada pelo jogador):
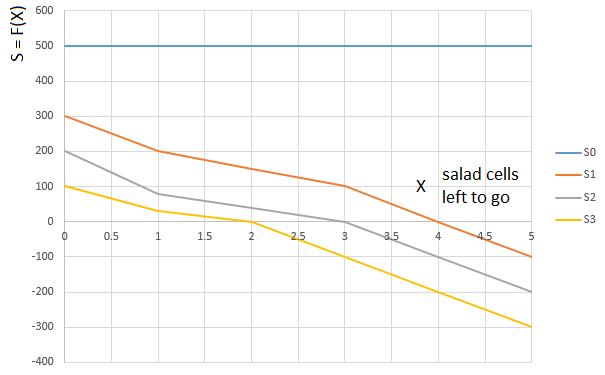
A curva
- função de avaliação (S) do número de células de alface na frente do jogador (0 ... 5), para um jogador com 0 cartas de alface na mão,
a curva
- a mesma função para um jogador com uma carta de salada na mão, etc.
A classificação final (E = Ks * S + Kc * C + Kp * P) leva em consideração:
- a quantidade extra de cenouras que o jogador receberá imediatamente antes de sua própria jogada,
- o caminho do jogador
- a quantidade de cenoura e alface nas mãos que afetam não linearmente a pontuação.
E aqui está como um computador é executado, escolhendo a próxima jogada com a pontuação heurística máxima:
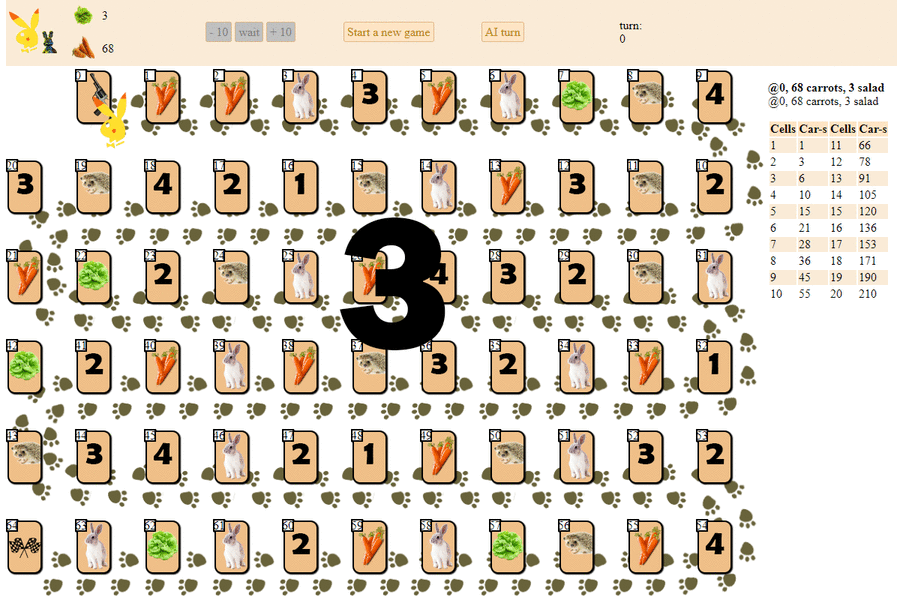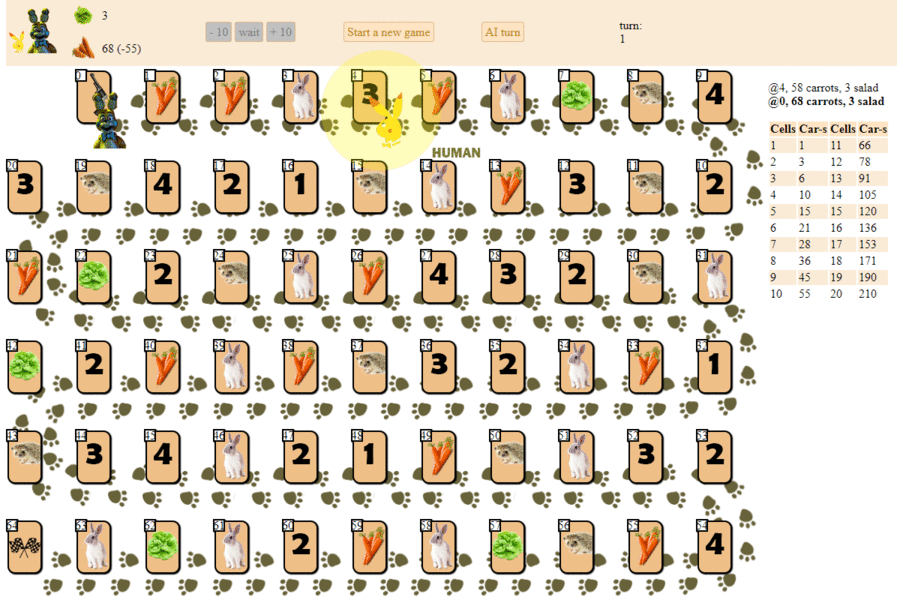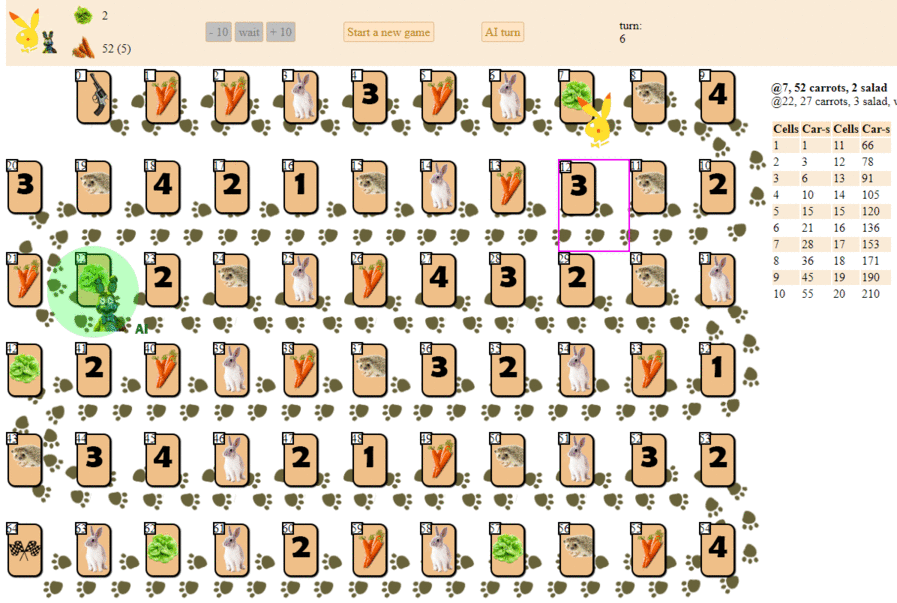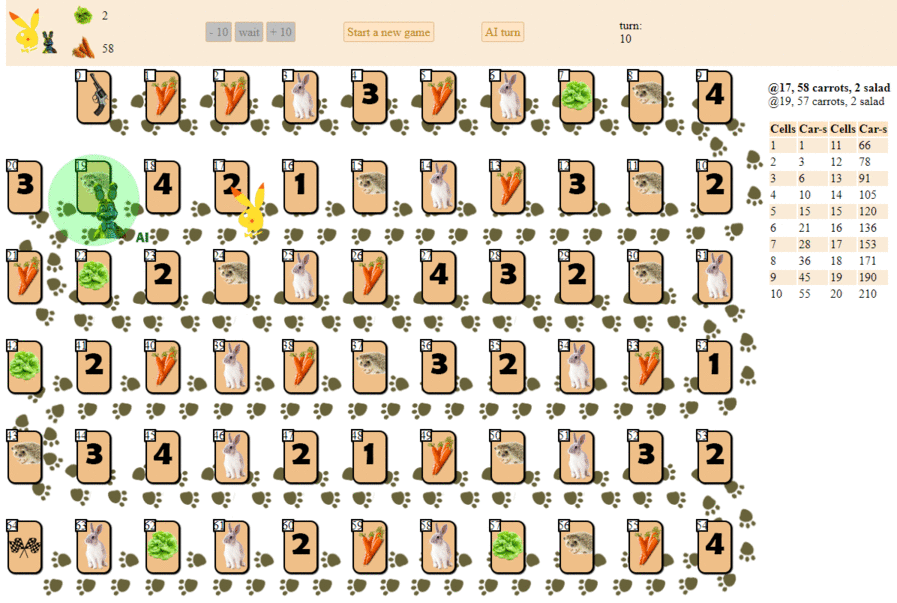
Em princípio, a estréia não é tão ruim. No entanto, não se deve esperar um bom jogo dessa IA: no meio do jogo, o “robô” verde começa a fazer movimentos repetidos e, no final, faz várias iterações de movimentos para a frente - para trás para o ouriço, até que finalmente termine. Em parte devido ao acaso, ele terminará atrás do jogador - uma pessoa por uma dúzia de jogadas.
Notas de implementaçãoO cálculo da avaliação é gerenciado por uma classe especial - EstimationCalculator. As funções para avaliar a posição em relação aos cartões de salada de cenoura são carregadas em matrizes no construtor estático da classe da calculadora. Na entrada, o método de estimativa de posição recebe o próprio objeto de posição e o índice do jogador, do "ponto de vista" do qual a posição é avaliada pelo algoritmo. Ou seja, a mesma posição do jogo pode receber várias classificações diferentes, dependendo de qual jogador os pontos virtuais são considerados.
Árvore de Decisão e Algoritmo Minimax
Usamos o algoritmo de tomada de decisão no jogo antagônico Minimax. Muito bom, na minha opinião, o algoritmo é descrito
neste post (tradução) .
Ensinamos o programa a "olhar" alguns passos à frente. Suponha que, a partir da posição atual (e o plano de fundo não seja importante para o algoritmo - como lembramos, o programa funciona como
um autômato de Moore ), numerado pelo número 1, o programa pode fazer dois movimentos. Temos duas posições possíveis, 2 e 3. A seguir vem a vez do jogador - a pessoa (no caso geral - o inimigo). A partir da 2ª posição, o oponente tem 3 jogadas, da terceira - apenas duas jogadas. A seguir, a vez de fazer um movimento novamente recai no programa, que, no total, pode fazer 10 movimentos em 5 posições possíveis:
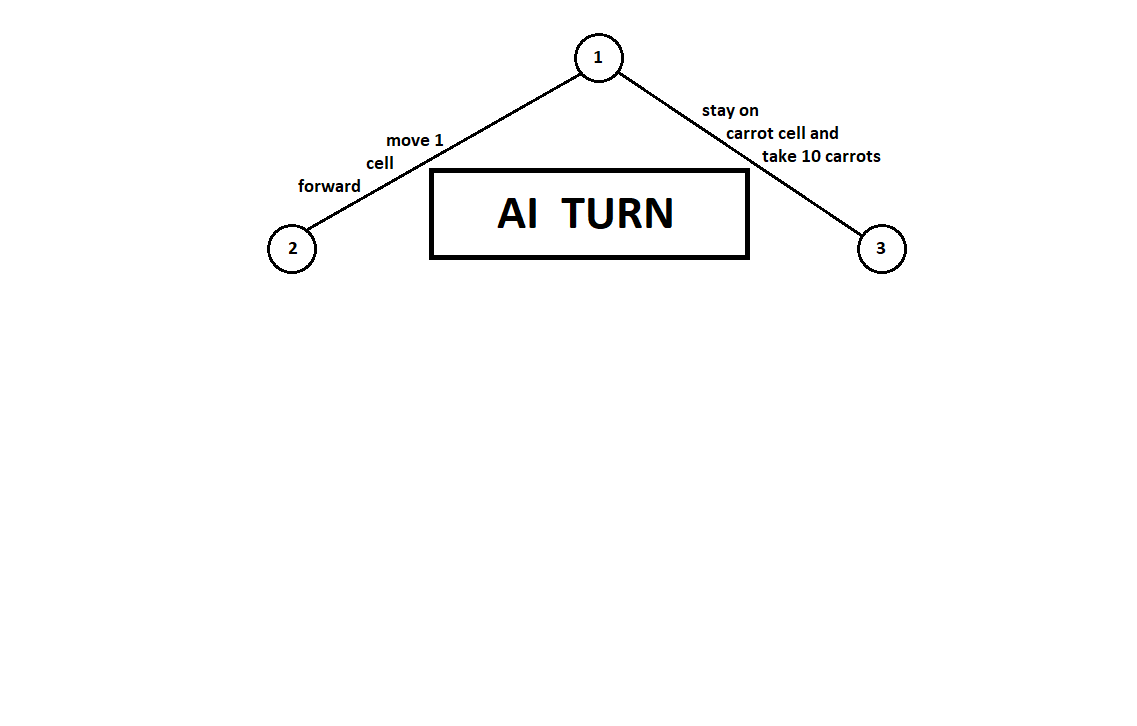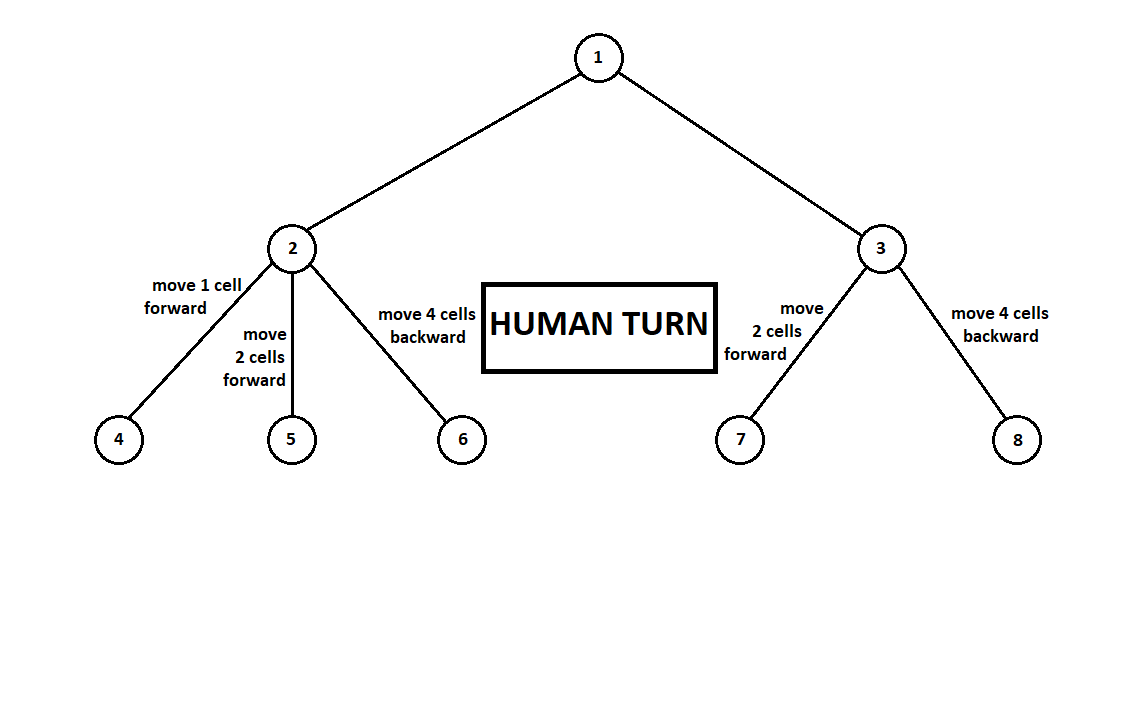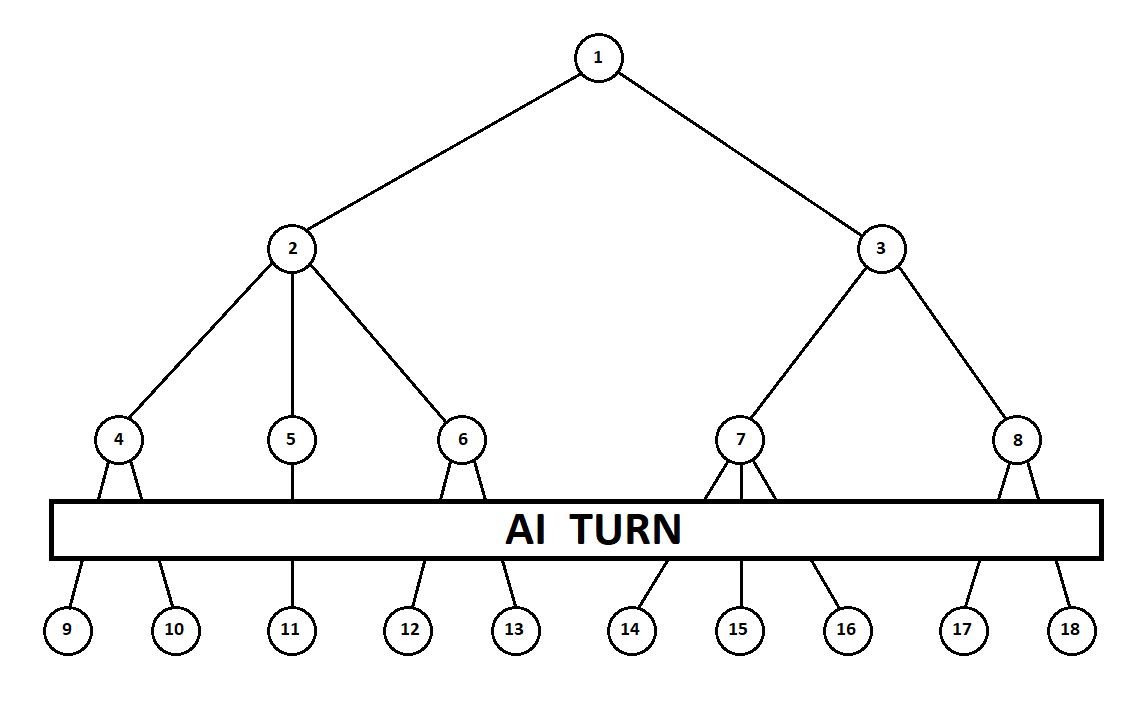
Suponha que, após o segundo movimento do computador, o jogo termine e cada uma das posições recebidas seja avaliada do ponto de vista do primeiro e do segundo jogadores. E já implementamos o algoritmo de avaliação. Vamos avaliar cada uma das posições finais (folhas da árvore 9 ... 18) na forma de um vetor
,
onde
- pontuação calculada para o primeiro jogador,
- pontuação do segundo jogador:
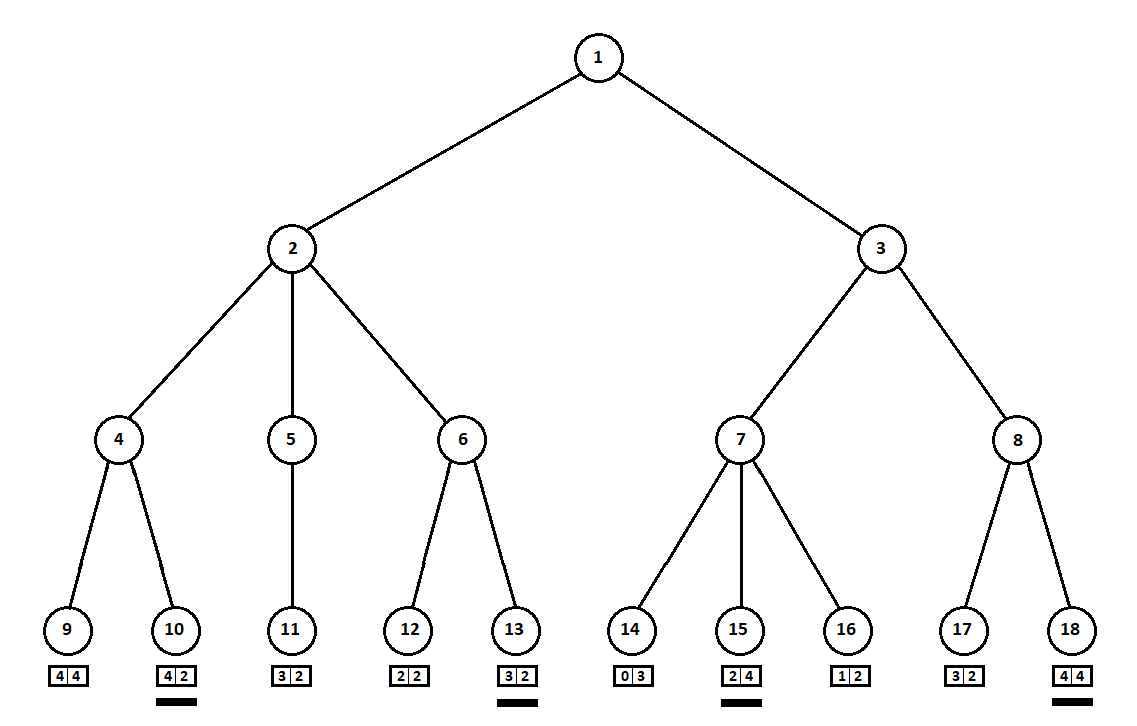
Como o computador faz a última jogada, obviamente escolherá as opções em cada uma das subárvores ([9, 10], [11], [12, 13], [14, 15, 16], [17, 18]) o que lhe dá uma classificação melhor. A questão imediatamente se coloca: por qual princípio se deve escolher a melhor posição?
Por exemplo, existem dois movimentos, após os quais temos posições com classificações [5; 5] e [2; 1] Avalia o primeiro jogador. Duas alternativas são óbvias:
- seleção de posição com o valor absoluto máximo da i-ésima pontuação para o i-ésimo jogador. Em outras palavras, o nobre piloto Leslie, ansioso pela vitória, sem considerar os concorrentes. Nesse caso, uma posição com uma estimativa de [5; 5]
- a escolha de uma posição com a classificação máxima em relação às estimativas dos concorrentes é o esperto professor Faith, que não perde a oportunidade de infligir truques sujos ao inimigo. Por exemplo, fique intencionalmente atrás de um jogador que planeja começar da segunda posição. Um item com classificação [2; 1]
Na minha implementação de software, criei o algoritmo de seleção de notas (uma função que mapeia o vetor de notas para um valor escalar para o i-ésimo jogador) um parâmetro personalizado. Outros testes mostraram, para minha surpresa, a superioridade da primeira estratégia - a escolha da posição pelo valor absoluto máximo
.
Recursos de implementação de softwareSe a primeira opção para escolher a melhor nota for especificada nas configurações da AI (classe TurnMaker), o código do método correspondente assumirá a forma:
int ContractEstimateByAbsMax(int[] estimationVector, int playerIndex) { return estimationVector[playerIndex]; }
O segundo método - o máximo em relação às posições dos concorrentes - é implementado um pouco mais complicado:
int ContractEstimateByRelativeNumber(int[]eVector, int player) { int? min = null; var pVal = eVector[player]; for (var i = 0; i < eVector.Length; i++) { if (i == player) continue; var val = pVal - eVector[i]; if (!min.HasValue || min.Value > val) min = val; } return min.Value; }
As estimativas selecionadas (sublinhadas na figura) são transferidas para o nível superior. Agora o inimigo precisa escolher uma posição, sabendo qual posição subsequente o algoritmo escolherá:
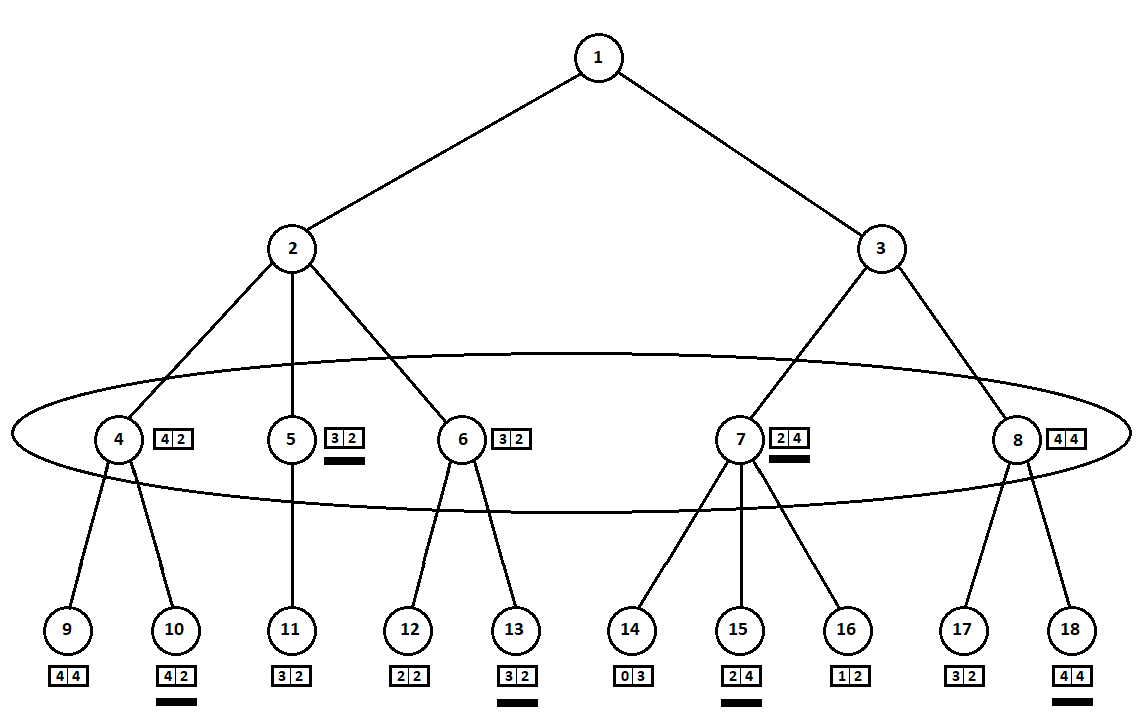
O adversário, obviamente, escolherá a posição com a melhor classificação para si (aquela em que a
segunda coordenada do vetor tiver o maior valor). Essas estimativas estão novamente sublinhadas no gráfico.
Finalmente, voltamos ao primeiro passo. O computador seleciona e ele prefere a movimentação com a maior primeira coordenada do vetor:
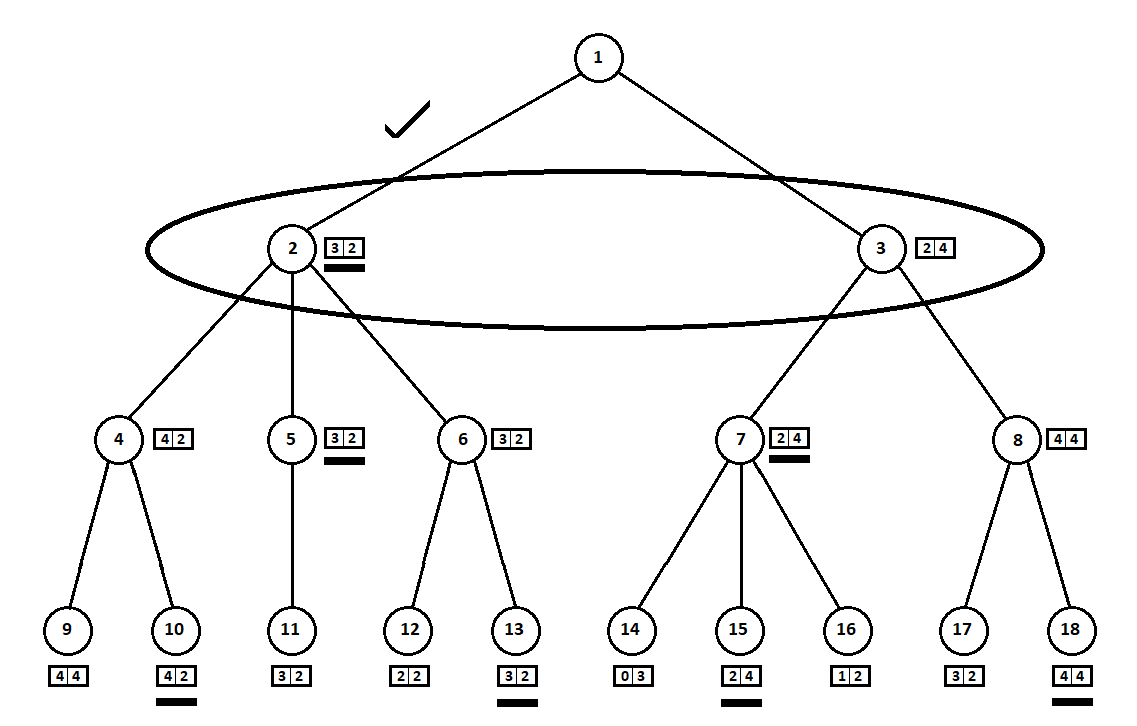
Assim, o problema está resolvido - um movimento quase ótimo é encontrado. Suponha que uma pontuação heurística de 100% nas posições das folhas em uma árvore indique um futuro vencedor. Então, nosso algoritmo escolherá inequivocamente a melhor jogada possível.
No entanto, a pontuação heurística é 100% precisa somente quando a posição
final do jogo é avaliada - um (ou vários) jogadores terminaram, o vencedor é determinado. Portanto, tendo a oportunidade de olhar para frente com N movimentos - o suficiente para vencer rivais com força igual, você pode escolher o movimento ideal.
Mas um jogo típico para 2 jogadores dura em média cerca de 30 a 40 movimentos (para três jogadores - cerca de 60 movimentos, etc.). De cada posição, um jogador geralmente pode fazer cerca de 8 movimentos. Consequentemente, uma árvore completa de posições possíveis para 30 movimentos consistirá em aproximadamente
= 1237940039285380274899124224 picos!
Na prática, construir e "analisar" uma árvore de aproximadamente 100.000 posições no meu PC leva cerca de 300 milissegundos. O que nos dá um limite na profundidade da árvore em 7 a 8 níveis (movimentos), se queremos esperar uma resposta do computador não mais que um segundo.
Recursos de implementação de softwareObviamente, é necessário um método recursivo para construir uma árvore de posições e encontrar a melhor jogada. Na entrada do método - a posição atual (na qual, como lembramos, o jogador já está fazendo um movimento) e o nível atual da árvore (número do movimento). Assim que descermos ao nível máximo permitido pelas configurações do algoritmo, a função retornará um vetor de estimativa de posição heurística do "ponto de vista" de cada um dos jogadores.
Uma adição importante : a descida abaixo da árvore também deve ser interrompida quando o jogador atual terminar. Caso contrário (se o algoritmo para selecionar a melhor posição em relação às posições de outros jogadores for selecionado), o programa poderá "pisar" no final por um longo tempo, "zombando" do oponente. Além disso, dessa forma, reduziremos um pouco o tamanho da árvore no final do jogo.
Se ainda não estamos no nível final de recursão, selecionamos os movimentos possíveis, criamos uma nova posição para cada movimento e passamos para a chamada recursiva do método atual.
Por que o Minimax?Na interpretação original dos jogadores são sempre dois. O programa calcula a pontuação exclusivamente a partir da posição do primeiro jogador. Assim, ao escolher a melhor posição, o jogador com o índice 0 procura uma posição com uma classificação máxima, o jogador com o índice 1 procura um mínimo.
No nosso caso, a classificação deve ser um vetor para que cada um dos N jogadores possa avaliá-la do seu "ponto de vista", à medida que a classificação sobe na árvore.
Tuning AI
Minha prática de jogar contra o computador mostrou que o algoritmo não é tão ruim, mas ainda inferior aos humanos. Decidi melhorar a IA de duas maneiras:
- otimizar a construção / travessia da árvore de decisão,
- melhorar heurísticas.
Otimização do algoritmo Minimax
No exemplo acima, poderíamos nos recusar a considerar a posição 8 e "salvar" 2 - 3 vértices da árvore:
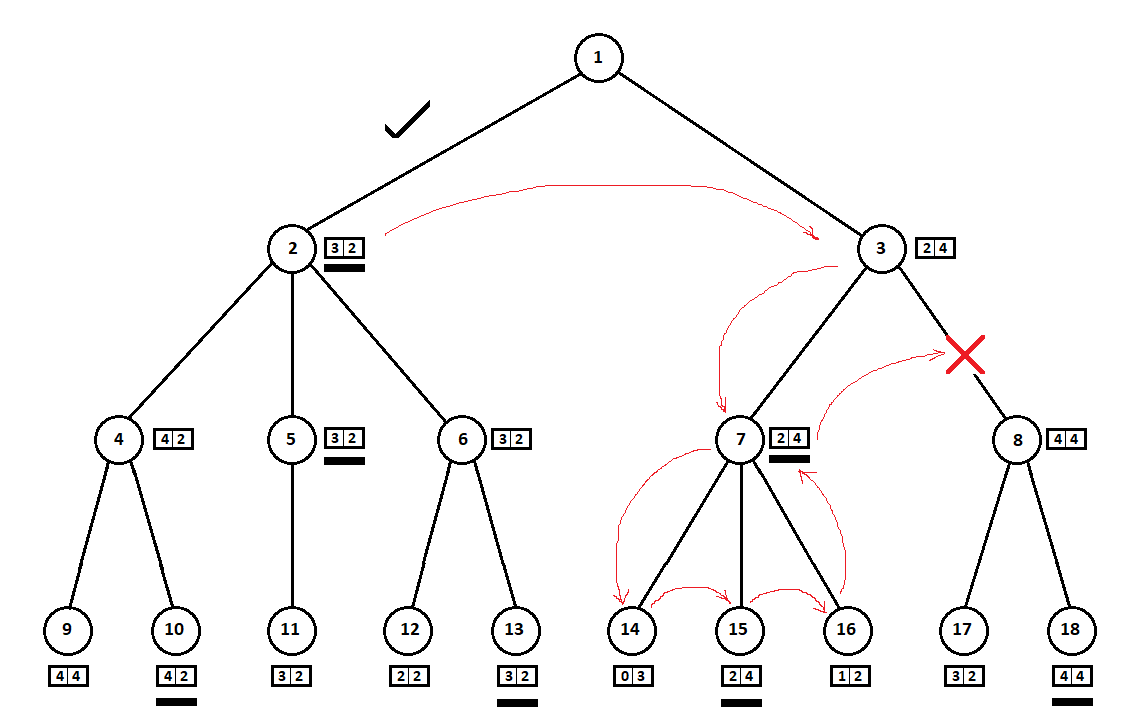
Andamos em torno da árvore de cima para baixo, da esquerda para a direita. Ignorando a subárvore começando na posição 2, deduzimos a melhor estimativa para o movimento 1 -> 2: [3, 2]. Ignorando a subárvore com a raiz na posição 7, determinamos a classificação atual (melhor para o movimento 3 -> 7): [2, 4]. Do ponto de vista do computador (primeiro jogador), a pontuação [2, 4] é pior que a pontuação [3, 2]. E como o oponente do computador escolhe a jogada da posição 3, qualquer que seja a pontuação da posição 8, a pontuação final da posição 3 será a priori pior que a pontuação obtida na terceira posição. Por conseguinte, a subárvore com a raiz na posição 8 não pode ser construída e não avaliada.
A versão otimizada do algoritmo Minimax, que permite cortar o excesso de subárvores, é chamada de
algoritmo de recorte alfa-beta . A implementação desse algoritmo exigirá pequenas modificações no código-fonte.
Recursos de implementação de softwareAlém disso, dois parâmetros inteiros são passados para o método CalcEstimate da classe TurnMaker - alfa, que é igual a int.MinValue inicialmente e beta, que é int.MaxValue. Além disso, depois de receber uma estimativa da movimentação atual em consideração, um pseudocódigo do formulário é executado:
e = _[0]
Uma característica importante da implementação de softwareo método de recorte alfa-beta, por definição, leva à mesma solução que o algoritmo Minimax "limpo". Para verificar se a lógica da tomada de decisão mudou (ou melhor, os resultados são jogadas), escrevi um teste de unidade no qual o robô fez 8 jogadas para cada um dos 2 oponentes (16 jogadas no total) e salvou a série de jogadas resultante - com opção de recorte desativado .
Em seguida, no mesmo teste, o procedimento foi repetido com a opção de recorte ativada . Depois disso, a sequência de movimentos foi comparada. A discrepância nos movimentos indica um erro na implementação do algoritmo de corte alfa-beta (falha no teste).
Menor otimização de recorte alfa-beta
Com a opção de recorte ativada nas configurações de AI, o número de vértices na árvore de posições foi reduzido em média 3 vezes. Este resultado pode ser um pouco melhorado.
No exemplo acima:

"coincidiu" com tanto sucesso que, antes da subárvore com o vértice na posição 3, examinamos a subárvore com o vértice na posição 2. Se a sequência fosse diferente, poderíamos começar com a "pior" subárvore e não concluir que não havia sentido em considerar a próxima posição .
Como regra geral, o recorte em uma árvore acaba sendo mais "econômico", seus vértices descendentes no mesmo nível (isto é, todos os movimentos possíveis da posição i) já são classificados pela estimativa da posição atual (sem olhar profundamente). Em outras palavras, supomos que o melhor movimento (do ponto de vista heurístico) tem maior probabilidade de obter uma nota final melhor. Assim, nós, com alguma probabilidade, classificamos a árvore para que a subárvore “melhor” seja considerada antes da “pior”, o que nos permitirá cortar mais opções.
A avaliação da posição atual é um procedimento caro. Se anteriormente bastava avaliar apenas as posições terminais (folhas), agora a avaliação é feita para todos os vértices da árvore. No entanto, como os testes mostraram, o número total de estimativas feitas ainda era um pouco menor do que na variante sem a classificação inicial de possíveis movimentos.
Recursos de implementação de softwareO algoritmo de corte alfa-beta retorna o mesmo movimento que o algoritmo Minimax original. Isso verifica o teste de unidade que escrevemos, comparando duas seqüências de movimentos (para um algoritmo com recorte e sem). O recorte alfa-beta com classificação , em geral, pode indicar um movimento diferente do quase ideal.
Para testar a operação correta do algoritmo modificado, você precisa de um novo teste. Apesar da modificação, um algoritmo com classificação deve produzir exatamente o mesmo vetor de estimativa final ([3, 2] no exemplo da figura) que o algoritmo sem classificação como o algoritmo Minimax original.
No teste, criei uma série de posições de teste e as selecionei de acordo com a “melhor” jogada, ativando e desativando a opção de classificação. Em seguida, ele comparou o vetor de avaliação obtido de duas maneiras.
Além disso, como as posições de cada um dos movimentos possíveis no vértice atual da árvore são classificadas por avaliação heurística, é implícito a idéia de descartar imediatamente algumas das piores opções. Por exemplo, um jogador de xadrez pode considerar um movimento no qual substitui sua torre por um golpe de peão. No entanto, "desenrolando" a situação em profundidade por 3, 4 ... movimentos para frente, ele notará imediatamente as opções quando, por exemplo, o oponente colocar o bispo de sua rainha sob ataque.
Nas configurações de IA, defino o vetor "recorte das piores opções". Por exemplo, um vetor no formato [0, 0, 8, 8, 4] significa que:
- olhando para um [0] e dois [0] passos adiante, o programa considerará todos os movimentos possíveis, porque 0 ,
- [8] [8] , 8 “” , , ,
- olhando cinco ou mais passos adiante [4], o programa avaliará não mais do que 4 “melhores” movimentos.
Com a classificação ativada para o algoritmo de recorte alfa-beta e um vetor semelhante nas configurações de recorte, o programa começou a gastar cerca de 300 milissegundos para selecionar um movimento quase ideal, “avançando mais” 8 passos à frente.Otimização Heurística
Apesar da quantidade decente de posições de vértices repetidas na árvore e “profundas”, olhando para o futuro em busca de um movimento quase ideal, a IA tinha várias fraquezas. Eu defini um deles como uma " armadilha de coelho ".Armadilha de lebre. ( 8 — 10 15), . “” ( !):
. :
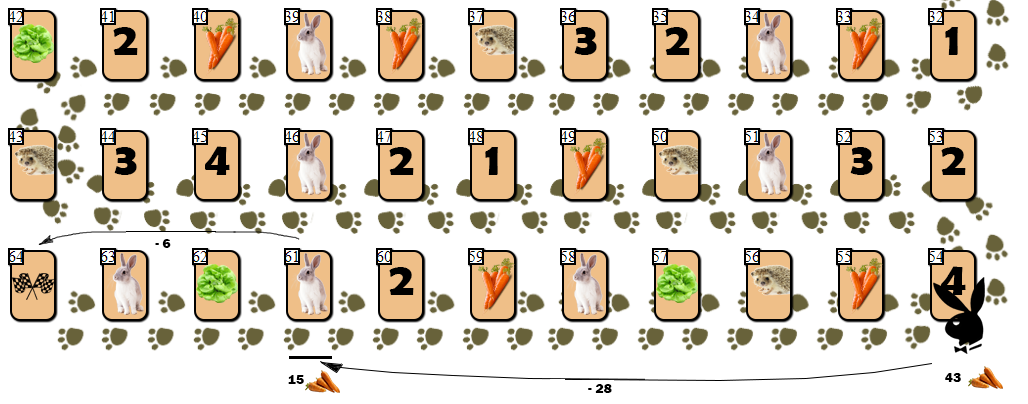
54 (43), — 10 55 . AI, , (61), 28 . , 6 9 ( 10 ).
, ( ), , 4 — 6 . , , , AI ?
,
, . AI . , , . “ ” :
65 — “” , , . , , , () .
Fatores de correção
Anteriormente, fornecendo uma fórmula para a estimativa heurística da posição atualE = Ks * S + Kc * C + Kp * P,mencionei, mas não descrevi, os fatores de correção.O fato é que tanto a fórmula em si quanto os conjuntos de funções , foram deduzidos por mim intuitivamente, com base nos chamados "Bom senso". No mínimo, gostaria de selecionar esses coeficientes Ks, Kc e Kp para que a estimativa seja o mais adequada possível. Como avaliar a "adequação" da avaliação? A avaliação é uma quantidade sem dimensão e só pode ser comparada com outra estimativa. Consegui encontrar a única maneira de refinar os coeficientes de correção:coloquei no programa uma série de “estudos” armazenados em um arquivo CSV com dados do formulário 45;26;2;f;29;19;0;f;2 ...
Essa linha significa literalmente o seguinte:- o primeiro jogador está no quadrado 45, ele tem 26 cartas de cenoura e 2 cartas de salada nas mãos, o jogador não perde um movimento (f = falso). O direito de mudar é sempre o primeiro jogador.
- o segundo jogador na cela 29, com 19 cartas de cenoura e sem cartas de salada, não perde nenhum movimento.
- a figura dois significa que, “decidindo” o estudo, presumi que o segundo jogador estivesse em uma situação vencedora.
Depois de colocar 20 esboços no programa, eu os "baixei" no cliente web do jogo e, em seguida, classifiquei cada um esboçado. Analisando o esboço, alternadamente fiz movimentos para cada um dos jogadores, até que decidi sobre o "vencedor". Depois de concluir a avaliação, enviei-a em uma equipe especial para o servidor.Depois de avaliar 20 estudos (é claro, valeria a pena analisar mais deles), avaliei cada um dos estudos pelo programa. Na avaliação, os valores de cada um dos fatores de correção, de 0,5 a 2, em incrementos de 0,1 - total = 4096 variantes de triplos de coeficientes. Se a pontuação do primeiro jogador for superior à pontuação do segundo jogador e uma instrução semelhante foi armazenada na linha do registro de estudo (o último valor da linha é 1), o "acerto" foi contado. Da mesma forma para uma situação de espelho. Caso contrário, uma nota foi contada. Como resultado, escolhi aqueles triplos para os quais a porcentagem de "acertos" era máxima (16 em 20). Foram lançados cerca de 250 de 4096 vetores, dos quais selecionei o “melhor”, novamente, “a olho” e o instalei nas configurações de IA.Sumário
Como resultado, recebi um programa de trabalho que, em regra, me supera na versão individual contra o computador. Estatísticas sérias de vitórias e derrotas para a versão atual do programa ainda não foram acumuladas. Talvez o ajuste fácil subsequente da IA torne minhas vitórias impossíveis. Ou quase impossível, já que o fator das células da lebre ainda permanece.Por exemplo, na lógica de escolher classificações (máximo absoluto ou máximo em relação a outros jogadores), eu definitivamente tentaria uma opção intermediária. No mínimo, se o valor absoluto da i-ésima pontuação do jogador for igual, é razoável escolher a jogada que leva à posição com um valor relativo maior da pontuação (um híbrido da nobre Leslie e da traiçoeira Feith).O programa é totalmente funcional para a versão com 3 jogadores. No entanto, há suspeitas de que a "qualidade" da IA se mova para jogar com três jogadores é menor do que para jogar com dois jogadores. No entanto, durante o último teste, perdi para o computador - talvez por negligência, avaliando casualmente a quantidade de cenouras em minhas mãos e chegando à linha de chegada com um excesso de "combustível".Até agora, o desenvolvimento futuro da IA é dificultado pela falta de uma pessoa - um "testador", ou seja, um oponente vivo de um "gênio" do computador. Eu próprio toquei o suficiente de Hare e Hedgehog para náusea e fui forçado a interromper no estágio atual.→ Link para o repositório com fonte