A matemática em Gamedev é simples. Matrizes e transformações afins

Olá pessoal! Meu nome é Grisha e sou o fundador da CGDevs. Hoje eu quero continuar o tópico de matemática no game dev. Em um artigo anterior , mostramos exemplos básicos de uso de vetores e integrais em projetos do Unity, e agora vamos falar sobre matrizes e transformações afins. Se você é bem versado em aritmética matricial; Você sabe o que é TRS e como trabalhar com ele; qual é a transformação do chefe de família - você provavelmente não encontrará nada de novo para si mesmo. Falaremos no contexto de gráficos 3D. Se você está interessado neste tópico - bem-vindo ao gato.



Vamos começar com um dos conceitos mais importantes no contexto do artigo - transformações afins . Transformações afins são, em essência, a transformação do sistema de coordenadas (ou espaço) multiplicando o vetor por uma matriz especial. Por exemplo, transformações como movimento, rotação, escala, reflexão, etc. As principais propriedades das transformações afins são que você fica no mesmo espaço (é impossível fazer bidimensional a partir de um vetor tridimensional) e que se as linhas se cruzam / são paralelas / foram cruzados antes da conversão, essa propriedade será preservada após a conversão. Além disso, eles têm muitas propriedades matemáticas que requerem conhecimento da teoria de grupos, conjuntos e álgebra linear, o que facilita o trabalho com eles.

Matriz TRS

O segundo conceito importante em computação gráfica é a matriz TRS . Usando-o, você pode descrever as operações mais comuns usadas ao trabalhar com gráficos de computador. Uma matriz TRS é uma composição de três matrizes de transformação. Matrizes de translação (translação), rotação em cada eixo (rotação) e escala (escala).
Ela é assim.



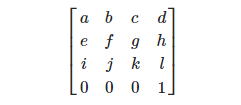
Onde:
O movimento é t = novo Vetor3 (d, h, l).
Dimensionamento - s = novo Vetor3 (novo Vetor3 (a, e, i) .magnitude, novo Vetor3 (b, f, j) .magnitude, novo Vetor3 (c, g, k) .magnitude);

Uma rotação é uma matriz do formulário:



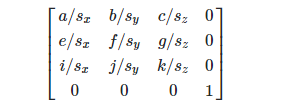
Agora vamos aprofundar um pouco mais o contexto do Unity. Para começar, a matriz TRS é uma coisa muito conveniente, mas não deve ser usada em qualquer lugar. Como uma simples indicação da posição ou adição de vetores em uma unidade funcionará mais rapidamente, mas em muitos algoritmos matemáticos, as matrizes são muitas vezes mais convenientes que os vetores. A funcionalidade TRS no Unity é amplamente implementada na classe Matrix4x4 , mas não é conveniente do ponto de vista da aplicação. Como, além de aplicar a matriz por multiplicação, geralmente é possível armazenar informações sobre a orientação do objeto e, para algumas transformações, eu gostaria de poder calcular não apenas a posição, mas também alterar a orientação do objeto como um todo (por exemplo, reflexão que não é implementada no Unity)

Todos os exemplos são dados abaixo para o sistema de coordenadas local (a origem do GameObject é considerada a origem das coordenadas, dentro da qual o objeto está localizado. Se o objeto é a raiz da hierarquia na unidade, a origem é o mundo (0,0,0)).

Como usando a matriz TRS, podemos basicamente descrever a posição de um objeto no espaço, precisamos de uma decomposição do TRS para os valores específicos de posição, rotação e escala do Unity. Para fazer isso, você pode escrever métodos de extensão para a classe Matrix4x4


Além disso, para um trabalho conveniente, você pode implementar algumas extensões de classe Transform para trabalhar com o TRS.


Nisso, as vantagens da unidade terminam, uma vez que as matrizes na unidade são muito pobres em operação. Muitos algoritmos requerem aritmética matricial, que não é implementada na unidade, mesmo em operações completamente básicas, como adicionar matrizes e multiplicar matrizes por um escalar. Além disso, devido à peculiaridade da implementação de vetores no Unity3d, também existem vários inconvenientes associados ao fato de você poder criar um vetor 4x4, mas não o 1x4. Como falaremos mais sobre a transformação do chefe de família para reflexões, primeiro implementamos as operações necessárias para isso.

Adicionar / subtrair e multiplicar por um escalar é simples. Parece bastante volumoso, mas não há nada complicado aqui, pois a aritmética é simples.


Mas, para reflexão, precisamos da operação de multiplicação de matrizes em um caso particular. Multiplicação de um vetor de dimensão 4x4 por 1x4 (transposto) Se você conhece a matemática de matrizes, sabe que, com essa multiplicação, precisa olhar para os números extremos da dimensão e obterá a dimensão da matriz na saída, ou seja, neste caso 4x4. Há informações suficientes sobre como as matrizes são multiplicadas, portanto não iremos pintar isso. Aqui está um exemplo de um caso específico que será útil no futuro.

Transformação familiar

Em busca de como refletir um objeto em relação a qualquer eixo, costumo encontrar conselhos para colocar uma escala negativa na direção necessária. Esse é um péssimo conselho no contexto do Unity, pois quebra muitos sistemas no mecanismo (cortes, colisões etc.) Em alguns algoritmos, isso se transforma em cálculos não triviais se você precisar refletir de maneira não trivial em relação ao Vector3.up ou Vector3.forward, mas em uma direção arbitrária. O método de reflexão em uma unidade pronta para uso não é implementado, então eu implementei o método Household .

A transformação de chefe de família é usada não apenas em computação gráfica, mas neste contexto é uma transformação linear que reflete um objeto em relação a um plano que passa pela “origem” e é determinado pelo normal ao plano. Em muitas fontes, é descrito de maneira bastante complicada e incompreensível, embora sua fórmula seja elementar.

H = I-2 * n * (n ^ T)

Onde H é a matriz de transformação, eu , no nosso caso, é Matrix4x4.identity e n = new Vector4 (planeNormal.x, planeNormal.y, planeNormal.z, 0). O símbolo T significa transposição, ou seja, após multiplicar n * (n ^ T) , obtemos uma matriz 4x4.

Os métodos implementados serão úteis e a gravação será muito compacta.


Importante: planeNormal deve ser normalizado (o que é lógico) e a última coordenada n deve ser 0, para que não haja efeito de alongamento na direção, pois depende do comprimento do vetor n.

Agora, por conveniência no Unity, implementamos o método de extensão para transformação


Isso é tudo por hoje, se esta série de artigos continuar interessante, também revelarei outras aplicações da matemática no desenvolvimento de jogos. Desta vez, não haverá projeto, pois todo o código é colocado no artigo, mas o projeto com aplicativo específico estará no próximo artigo. Na imagem, você pode adivinhar o que será o próximo artigo.



Obrigado pela atenção!