Precisa de mais borrões diferentes

A desfocagem da imagem com o filtro Gaussian Blur é amplamente usada em uma ampla variedade de tarefas. Mas, às vezes, você quer um pouco mais de variedade do que apenas um filtro para todas as ocasiões, em que apenas um parâmetro se presta a ajustes - seu tamanho. Neste artigo, veremos várias outras implementações de desfoque.

1. Introdução

O efeito Gaussian Blur é uma operação linear e representa matematicamente uma convolução da imagem com a matriz do filtro. Nesse caso, cada pixel da imagem é substituído pela soma dos pixels próximos capturados com certos fatores de ponderação.

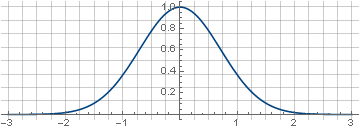
O filtro é chamado gaussiano porque é construído a partir de uma função conhecida como gaussiana, $$$e ^ {- x ^ 2}$ :



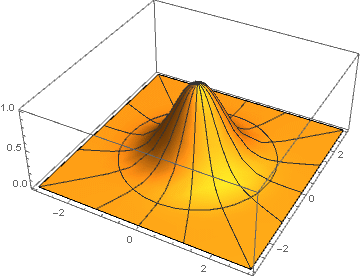
uma versão bidimensional obtida pela sua rotação em torno do eixo das ordenadas, $$$e ^ {- (x ^ 2 + y ^ 2)}$ :



Aqui para cada par de coordenadas $$$(x, y)$ a distância ao centro é calculada pela fórmula $$$\ sqrt {x ^ 2 + y ^ 2}$ , que é passado como argumento para a função gaussiana - e, como você pode ver facilmente, $$$e ^ {- \ left (\ sqrt {x ^ 2 + y ^ 2} \ right) ^ 2}$ reduzido a $$$e ^ {- (x ^ 2 + y ^ 2)}$ .

Matriz construída em um segmento $$$[- 3,3]$ e com algum nível de amostragem, ficará assim:

$$

$$\ left (\ begin {array} {ccccccc} 1,52 \ times 10 ^ {- 8} e ​​2,26 \ times 10 ^ {- 6} & 0,0000454 & 0,000123 & 0,0000454 & 2,26 \ times 10 ^ {- 6} & 1,52 \ vezes 10 ^ {- 8} \\ 2,26 \ vezes 10 ^ {- 6} & 0,000335 & 0,00674 & 0,0183 & 0,00674 & 0,000335 & 2,26 \ times 10 ^ {- 6} \\ 0,0000454 & 0,00674 & 0,135 & 0,368 & 0,135 & 0.00674 & 0.0000454 \\ 0.000123 & 0.0183 & 0.368 & 1.00 & 0.368 & 0.0183 & 0.000123 \\ 0.0000454 & 0.00674 & 0.135 & 0.368 & 0.135 & 0.00674 & 0.0000454 \\ 2.26 \ times 10 ^ {- 6} & 0.000335 & 0.00674 & 0,0183 & 0,00674 & 0,000335 & 2,26 \ times 10 ^ {- 6} \\ 1,52 \ times 10 ^ {- 8} & 2,26 \ times 10 ^ {- 6} & 0,0000454 & 0,000123 & 0,0000454 & 2,26 \ times 10 ^ { -6} & 1,52 \ times 10 ^ {- 8} \\ \ end {array} \ right)$$

Ou, se considerarmos os valores dos elementos da matriz como um nível de brilho, assim:



Em termos de processamento de sinal, isso é chamado de resposta ao impulso, uma vez que é exatamente isso que parecerá o resultado da convolução desse filtro com um único impulso (neste caso, um pixel).

Inicialmente, um gaussiano é definido em um intervalo infinito. Porém, devido ao fato de decair rapidamente, é possível excluir dos cálculos valores próximos de zero - pois eles ainda não afetarão o resultado. Em aplicações reais, a normalização de valores também é necessária para que, após a convolução, o brilho da imagem não mude; e no caso de desfocar uma imagem em que cada pixel tenha a mesma cor, a própria imagem não deve mudar.

Por conveniência, a normalização também é freqüentemente usada em coordenadas, introduzindo um parâmetro adicional $$$\ sigma$ (lido como "sigma") - para considerar um argumento no intervalo $$$[- 1,1]$ e $$$\ sigma$ determina a taxa de compressão do Gaussian:

$$

$$\ frac {e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}}} {2 \ pi \ sigma ^ 2}$$

Divisor de normalização $$$2 \ pi \ sigma ^ 2$ aqui obtido analiticamente através de uma integral definida no infinito:

$$

$$\ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}} \, dx dy = 2 \ pi \ sigma ^ 2$$

Devido ao fato de que a igualdade mantém $$$e ^ {- \ left (x ^ 2 + y ^ 2 \ right)} = e ^ {- x ^ 2} e ^ {- y ^ 2}$ O desfoque gaussiano pode ser implementado sequencialmente, primeiro nas linhas e depois nas colunas - o que permite economizar bastante em cálculos. Nesse caso, é necessário usar a fórmula de normalização para o caso unidimensional -

$$

$$\ frac {e ^ {- \ frac {x ^ 2} {2 \ sigma ^ 2}}} {\ sqrt {2 \ pi \ sigma ^ 2}}$$

Iniciar

Para um filtro arbitrário, primeiro precisamos definir nossa própria função de atenuação de uma variável $$$f$ , a partir do qual a função de duas variáveis ​​é obtida por rotação, substituindo $$$x$ em $$$\ sqrt {x ^ 2 + y ^ 2}$ onde $$$x$ e $$$y$ estas são as coordenadas do elemento da matriz no intervalo $$$(- 1,1)$ , e que é usado para preencher os elementos da matriz. A normalização não será considerada analiticamente, mas um somatório direto de todos os elementos da matriz - isso é mais simples e mais preciso - pois, após a discretização, a função é "reduzida" e o valor da normalização depende do nível de discretização.

Caso os elementos da matriz sejam numerados do zero, a coordenada $$$x$ ou $$$y$ é calculado pela fórmula

$$

$$\ frac {2 index} {size-1} -1$$

onde $$$index$ - o número de série do elemento na linha ou coluna, e $$$tamanho$ - número total de elementos.

Por exemplo, para uma matriz 5 por 5, ficaria assim:

$$

$$\ left (\ begin {array} {ccccc} f (-1, -1) & f \ left (- \ frac {1} {2}, - 1 \ right) ef (0, -1) ef \ left (\ frac {1} {2}, - 1 \ right) & f (1, -1) \\ f \ left (-1, - \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2}, - \ frac {1} {2} \ right) & f \ left (0, - \ frac {1} {2} \ right) & f \ left (\ frac { 1} {2}, - \ frac {1} {2} \ right) & f \ left (1, - \ frac {1} {2} \ right) \\ f (-1,0) & f \ left (- \ frac {1} {2}, 0 \ direita) & f (0,0) & f \ esquerda (\ frac {1} {2}, 0 \ direita) ef (1,0) \\ f \ left (-1, \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2}, \ frac {1} {2} \ right) & f \ left (0, \ frac {1} {2} \ right) & f \ left (\ frac {1} {2}, \ frac {1} {2} \ right) & f \ left (1, \ frac {1} {2 } \ right) \\ f (-1,1) & f \ left (- \ frac {1} {2}, 1 \ right) ef (0,1) & f \ left (\ frac {1} { 2}, 1 \ direita) ef (1,1) \\ \ end {matriz} \ direita)$$

Ou, se excluirmos valores de limite que ainda são zero, as coordenadas serão calculadas pela fórmula

$$

$$\ frac {2 tamanho do índice + 1} {tamanho}$$

e a matriz assumirá a forma

$$

$$\ left (\ begin {array} {ccccc} f \ left (- \ frac {4} {5}, - \ frac {4} {5} \ right) & f \ left (- \ frac {2} { 5}, - \ frac {4} {5} \ right) & f \ left (0, - \ frac {4} {5} \ right) & f \ left (\ frac {2} {5}, - \ frac {4} {5} \ right) & f \ left (\ frac {4} {5}, - \ frac {4} {5} \ right) \\ f \ left (- \ frac {4} {5 }, - \ frac {2} {5} \ right) & f \ left (- \ frac {2} {5}, - \ frac {2} {5} \ right) & f \ left (0, - \ frac {2} {5} \ right) & f \ left (\ frac {2} {5}, - \ frac {2} {5} \ right) & f \ left (\ frac {4} {5}, - \ frac {2} {5} \ right) \\ f \ left (- \ frac {4} {5}, 0 \ right) & f \ left (- \ frac {2} {5}, 0 \ right ) & f (0,0) & f \ left (\ frac {2} {5}, 0 \ right) & f \ left (\ frac {4} {5}, 0 \ right) \\ f \ left ( - \ frac {4} {5}, \ frac {2} {5} \ right) & f \ left (- \ frac {2} {5}, \ frac {2} {5} \ right) & f \ left (0, \ frac {2} {5} \ right) & f \ left (\ frac {2} {5}, \ frac {2} {5} \ right) & f \ left (\ frac {4} {5}, \ frac {2} {5} \ right) \\ f \ left (- \ frac {4} {5}, \ frac {4} {5} \ right) & f \ left (- \ frac {2} {5}, \ frac {4} {5} \ right) & f \ left (0, \ frac {4} {5} \ right) & f \ left (\ frac {2} {5}, \ frac {4} {5} \ right) & f \ left (\ frac {4} {5}, \ frac {4} {5} \ right) \\ \ end {array} \ right)$$

Após os elementos da matriz serem calculados pela fórmula, é necessário calcular a soma e dividir a matriz nela. Por exemplo, se obtivermos uma matriz

$$

$$\ left (\ begin {array} {ccc} 1 & 4 & 1 \\ 4 & 20 & 4 \\ 1 & 4 & 1 \\ \ end {array} \ right)$$

então a soma de todos os seus elementos será 40 e, após a normalização, assumirá a forma

$$

$$\ left (\ begin {array} {ccc} \ frac {1} {40} e \ frac {1} {10} e \ frac {1} {40} \\ \ frac {1} {10} e \ frac {1} {2} e \ frac {1} {10} \\ \ frac {1} {40} & \ frac {1} {10} e \ frac {1} {40} \\ \ end {array } \ right)$$

e a soma de todos os seus elementos se torna 1.

Atenuação linear

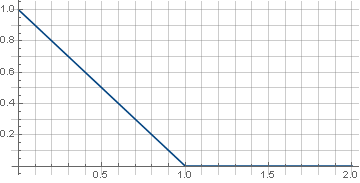
Primeiro, pegue a função mais simples - a linha:

$$

$$\ left \ {\ begin {array} {ll} 1-x, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

Uma definição contínua por partes aqui exige que a função seja garantida como zero e nenhum artefato apareça nos cantos da matriz durante a rotação. Além disso, como a rotação usa a raiz da soma dos quadrados das coordenadas, que é sempre positiva, basta determinar a função apenas na parte positiva dos valores. Como resultado, obtemos:

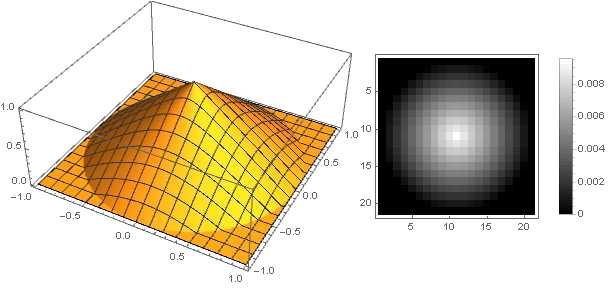
Atenuação linear suave

Uma transição nítida de uma linha oblíqua para zero funções pode causar uma contradição com um senso de beleza. Para resolvê-lo, a função nos ajudará.

$$

$$1- \ frac {n x-x ^ n} {n-1}$$

em que $$$n$ determina a "rigidez" da docking, $$$n> 1$ . Por exemplo $$$n = 3$ nós temos

$$

$$\ left \ {\ begin {array} {ll} 1- \ frac {3 xx ^ 3} {2}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

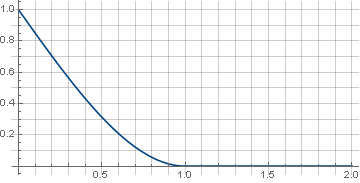
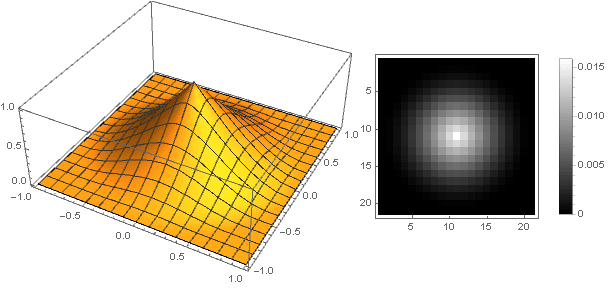
e o próprio filtro parecerá

Atenuação hiperbólica

O filtro pode ser tornado mais "nítido" e mais suavemente indo para zero, assumindo outra função, por exemplo, uma hipérbole e garantindo uma transição suave para zero, somando uma parábola.



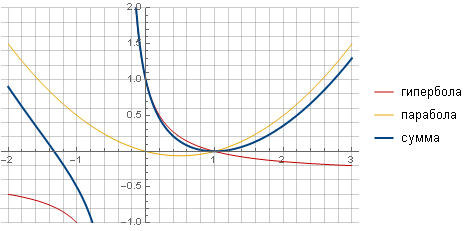
Após todos os cálculos e simplificações, obtemos a fórmula

$$

$$\ left \ {\ begin {array} {ll} \ frac {(x-1) ^ 2 (k x + k + 1)} {(k + 1) (k x + 1)}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

em que parâmetro $$$k> 0$ determina a natureza da atenuação:



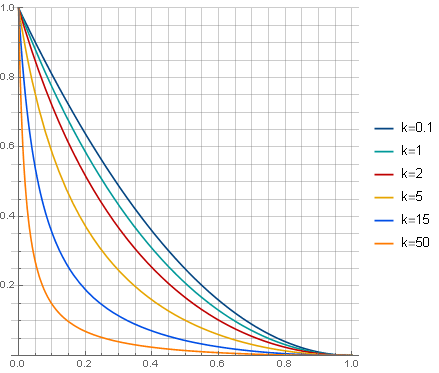
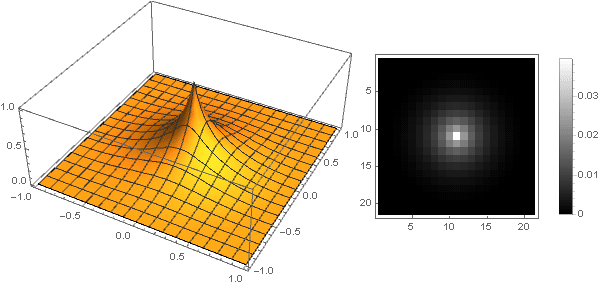
e o próprio filtro procurará (por $$$k = 5$ ) como

Efeito bokeh

Você pode seguir outro caminho - para tornar a parte superior do filtro não afiada, mas estúpida. A maneira mais fácil de implementar isso é definir a função de amortecimento como uma constante:

$$

$$\ left \ {\ begin {array} {ll} 1, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

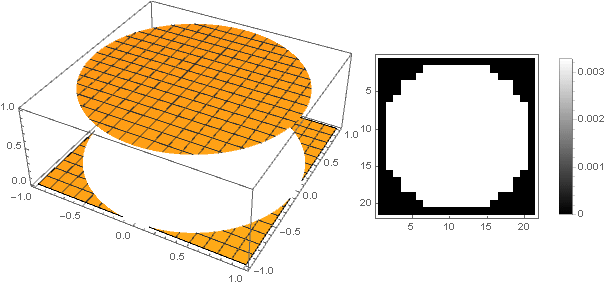
Mas, neste caso, temos uma forte pixelização, que contrasta com o senso de beleza. Para torná-lo mais suave nas bordas, uma parábola de ordem superior nos ajudará, a partir da qual, movendo-a ao longo do eixo ordenado e quadrando-o, obtemos

$$

$$\ left \ {\ begin {array} {ll} \ left (1-x ^ n \ right) ^ 2, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

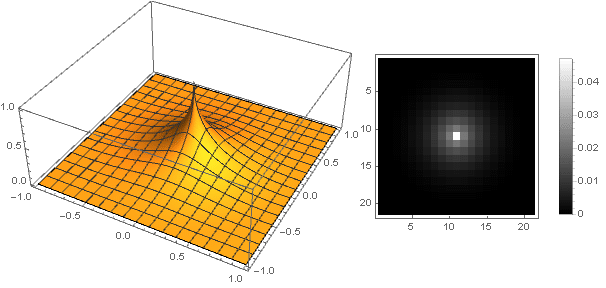
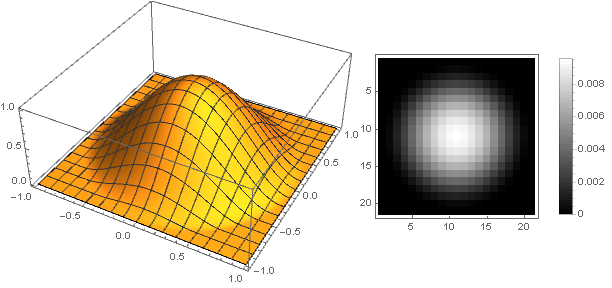
Parâmetro variável $$$n$ Você pode obter uma ampla variedade de opções de filtro:

$$

$$n = 0,5$$

$$

$$n = 2$$

$$

$$n = 10$$

$$

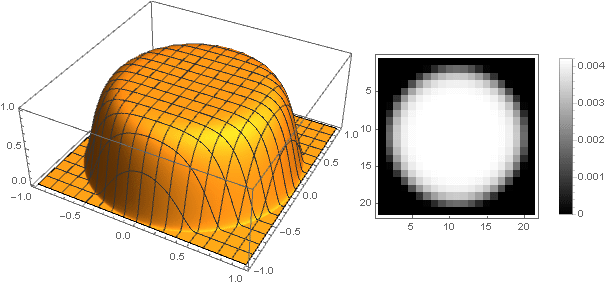
$$n = 50$$

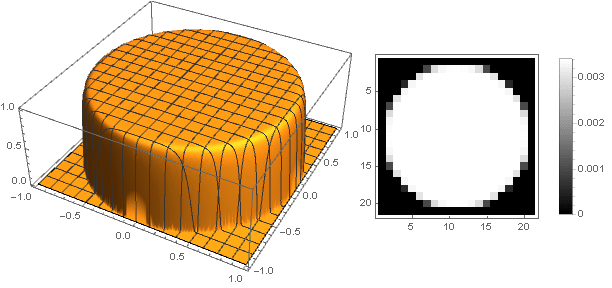
E modificando ligeiramente a função de amortecimento, você pode tornar o anel nas bordas do filtro mais pronunciado, por exemplo:

$$

$$\ left \ {\ begin {array} {ll} \ left (1-x ^ n \ right) ^ 2 \ left (d + x ^ m \ right), & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

Aqui parâmetro $$$d$ determina a altura do centro e $$$m$ - a nitidez da transição para as bordas.
Para $$$d = 0,2, m = 2, n = 10$ nós temos



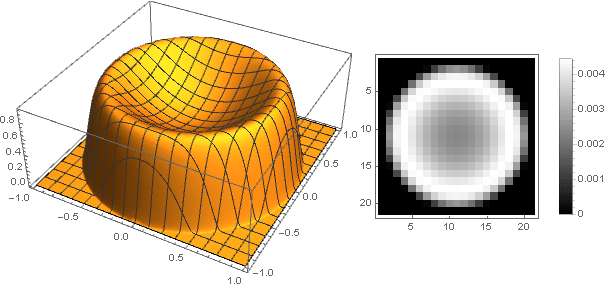
mas para $$$d = 0, m = 12, n = 2$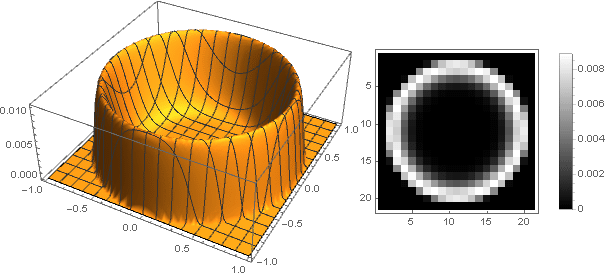

Variações gaussianas

A função do próprio gaussiano também pode ser modificada diretamente. A maneira mais óbvia de fazer isso é parametrizar o expoente - não o consideraremos agora, mas tomaremos uma opção mais interessante:

$$

$$\ left \ {\ begin {array} {ll} e ^ {\ frac {kx ^ 2} {x ^ 2-1}}, & -1 <x <1 \\ 0 e, caso contrário, \\ \ end { array} \ right.$$

Devido ao fato de que com $$$x$ denominador da unidade $$$x ^ 2-1$ tende a fração zero $$$\ frac {k x ^ 2} {x ^ 2-1}$ tende a menos infinito, e o expoente em si também tende a zero. Assim, dividindo por $$$x ^ 2-1$ permite compactar o domínio da definição de função com $$$(- \ infty, \ infty)$ antes $$$(- 1,1)$ . Além disso, quando $$$x = \ pm 1$ devido à divisão por zero ( $$$1 ^ 2-1 = 0$ ) o valor da função não está definido, mas possui dois limites - o limite, por um lado (a partir do interior), é zero e, por outro lado, o infinito:

$$

$$\ underset {x \ to 1 ^ -} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = 0$$

$$

$$\ underset {x \ to 1 ^ +} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = \ infty$$

Como os valores dos limites não estão incluídos no intervalo, zero no limite de um lado é suficiente. Curiosamente, essa propriedade se estende a todas as derivadas dessa função, o que garante uma correspondência perfeita com zero.

Parâmetro $$$k$ determina a semelhança com a gaussiana - quanto maior, mais forte é a semelhança - devido ao fato de uma seção cada vez mais linear $$$\ frac {1} {x ^ 2-1}$ cair no centro da função. Pode-se supor que, devido a isso, no limite, você possa obter o gaussiano original - mas, infelizmente, não - as funções ainda são diferentes.



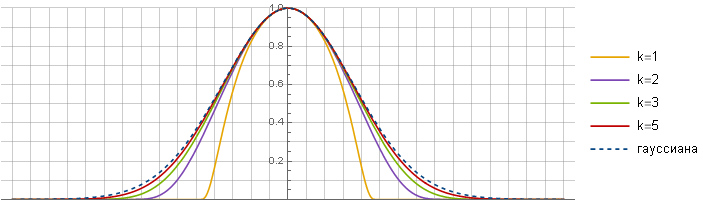
Agora você pode ver o que aconteceu:

$$

$$k = 5$$

$$

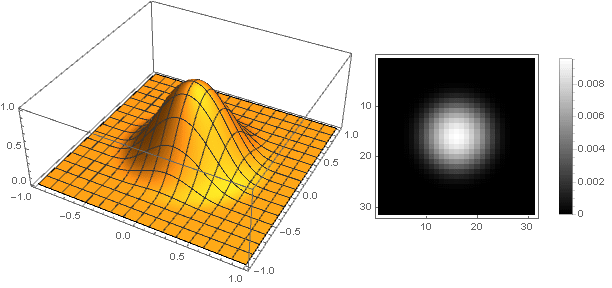
$$k = 2$$

$$

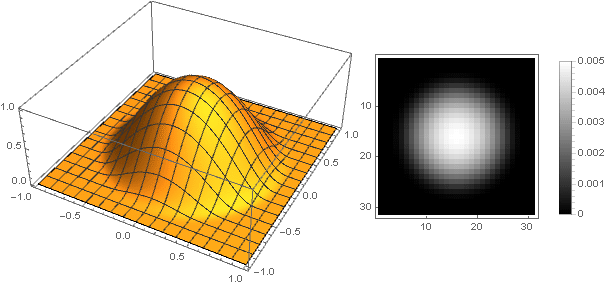
$$k = 0,5$$

$$

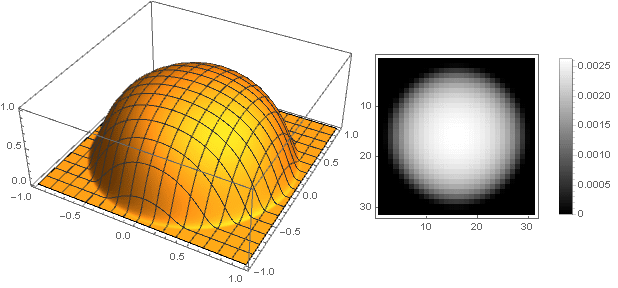
$$k = 0,1$$

$$

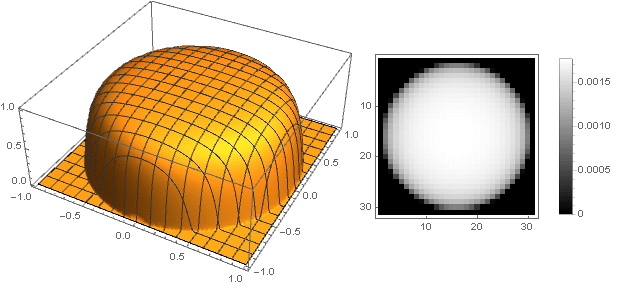
$$k = 0,01$$

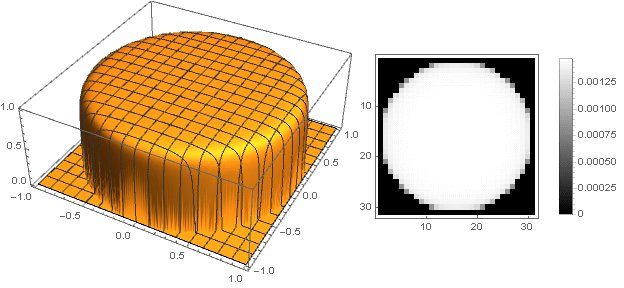
Variações de forma

Alterando a função de transição de duas coordenadas para uma $$$\ sqrt {x ^ 2 + y ^ 2}$ , você pode obter outras formas, não apenas um disco. Por exemplo:

$$

$$f \ left (\ frac {\ left | x-y \ right | + \ left | x + y \ right |} {2} \ right)$$

$$

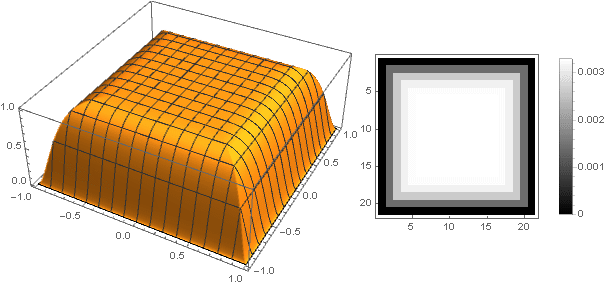
$$f (\ esquerda | x \ direita | + \ esquerda | y \ direita |)$$

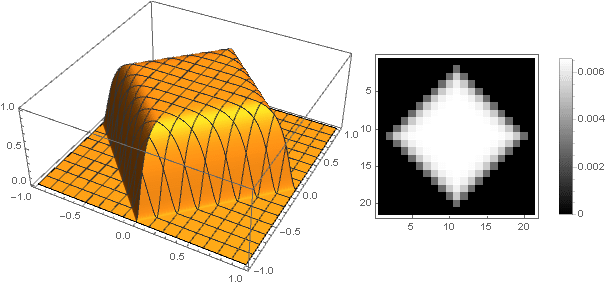
Ao passar para números complexos, é possível construir figuras mais complexas:

$$

$$f \ left (\ frac {\ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {0} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac { 2} {3}} \ right) \ right |} {\ sqrt {3}} \ right)$$

$$

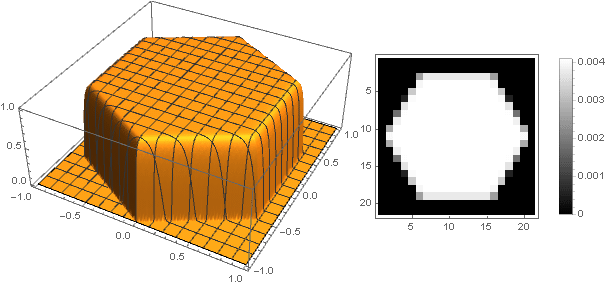
$$f \ biggl (10 \ esquerda | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {8}} \ right) \ right | \ biggr) \ cdot f (\ left | x + iy \ direita |)$$

$$

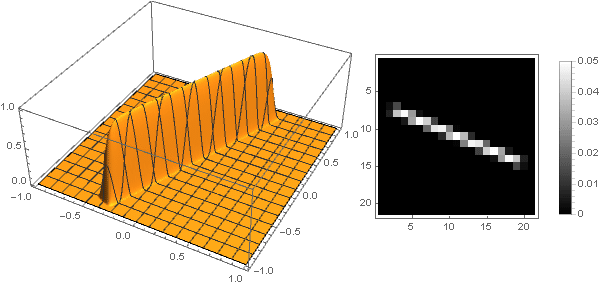
$$f \ biggl (\ biggl | 5 \ left | x + iy \ right | (x + iy) \ Re \ biggl (\ cos \ left (\ frac {5} {2} \ arg (x + iy) \ right ) \ biggr) \ biggr | \ biggr) \ cdot f (\ esquerda | x + iy \ direita |)$$

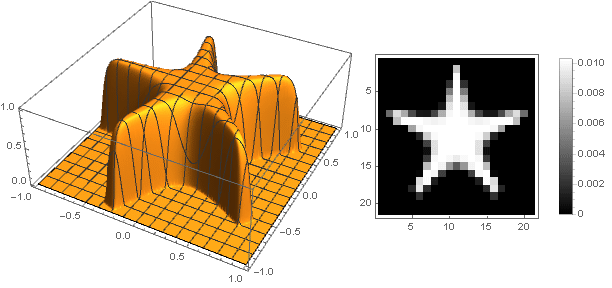
Nesse caso, você deve garantir que, ao converter coordenadas, não ultrapasse o intervalo $$$(0,1)$ - bem, ou vice-versa, redefina a função de amortecimento para valores negativos do argumento.

Alguns exemplos específicos

Um artigo não seria completo sem testes práticos em imagens específicas. Como não temos trabalho científico, também não tiraremos a imagem de Lena - levaremos algo macio e fofo:


















Os mesmos filtros, mas para texto:

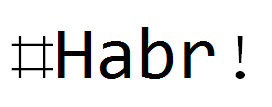
Conclusão

Da mesma forma, você pode criar filtros mais complexos, incluindo aqueles com nitidez ou contornos; e também modificar aqueles já considerados.

De particular interesse é a filtragem não linear, quando os valores dos coeficientes do filtro dependem das coordenadas ou da imagem sendo filtrada diretamente - mas isso já é assunto para outros estudos.

Mais detalhadamente, a derivação de funções para ancorar com uma constante é considerada aqui . As funções de janela consideradas aqui também podem ser usadas como a função de atenuação - tudo o que é necessário é escalar o argumento c (0,1) para ( $$$\ frac {1} {2}$ , 1) ou considere inicialmente as funções da janela pela fórmula $$$\ frac {1} {2} \ left (f \ left (\ frac {t x + 1} {t-1} \ right) -f \ left (\ frac {t x-1} {t-1} \ right) \ right)$ .

O documento fonte do Wolfram Mathematica deste artigo pode ser baixado aqui .