Em vez do prefácio
Suponha que, sentado na poltrona quente à noite, um pensamento louco lhe ocorreu: "Hmm, por que não descubro por que os hiperparâmetros do modelo são selecionados aleatoriamente e por que tudo funciona?"
Esta é uma ladeira escorregadia - você acha que bastam algumas noites com uma leitura lenta do capítulo “Aprendizado profundo” ou clipes de 5 minutos no YouTube de vários MOOCs; de fato, para criar entendimento, e não sua ilusão, é necessária uma quantidade decente de tempo (bem, certamente não menos de seis meses para os mais fanáticos); mas o mais triste é que o lucro desse evento não é óbvio - felizmente (ou infelizmente), o mundo não está organizado de acordo com as leis da matemática, e se você é médico em física três vezes, alguns modelos ainda funcionarão melhor apenas se você participar eles têm mais dados pré-processados ou constroem um conjunto enorme.
Considero que é meu dever adverti-lo de que este é um caminho curvo e é possível que os investimentos em matemática não sejam recompensados assim que desejamos. Mas a matemática é interessante por si só, quaisquer que sejam as aplicações. Além disso, se você estiver interessado, e o que acontece nessa caixa preta com hiperparâmetros, isso significa que a matemática provavelmente não é indiferente a você.
Outra coisa sobre minhas recomendações: não gosto de literatura matemática, repleta de índices, pérolas como “a_ijk com três sublinhados e um chapéu conjugado”. Acredito que idéias são mais importantes que conclusões rigorosas. Ao mesmo tempo, as idéias não devem cair nas "mãos", tudo deve ser bastante rigoroso. Não gosto de livros como Bourbaki e Knut. Na minha opinião, esses livros destinam-se a qualquer coisa, mas não à leitura e não ao estudo do assunto. Eles são bons como links e como enciclopédias.
No final, citarei algo de Bertrand Russell:
Euclides desprezava a utilidade prática que Platão introduzia. Eles dizem que um aluno, depois de ouvir as evidências, perguntou o que ele ganhou estudando geometria; então Euclides chamou um escravo e disse: "Dê um centavo ao jovem, porque ele certamente deve se beneficiar do que estuda".
Agora vou passar para a parte principal.
Pré-requisitos
- Presumo que você seja mais ou menos orientado em um curso escolar de matemática.
- Suponho que você não esteja totalmente em inglês com "você", uma vez que muita literatura e cursos são escritos e narrados nesse idioma. O inglês matemático não é tão assustador quanto o inglês em geral; este é um vocabulário bastante limitado, com frases construídas de maneira padronizada, sem uma confusão de tempo, sem uma profusão de cores, etc.
- Presumo que você tenha uma corda com a qual possa se amarrar a uma cadeira.
Níveis de dificuldade
Não é segredo que muita literatura foi escrita sobre cada disciplina matemática e, às vezes, até a simples escolha do livro certo se torna um problema. Vou destacar vários níveis de complexidade na literatura que você sabia onde se meter e onde escalar (até agora) não era necessário (ou o que você pode recorrer para obter informações mais completas).
- Traga-o - o cavalo de batalha principal; Estes são os livros chamados "must have".
- Me machuque bastante - um nível superior, permite que você observe o nível 1 do ponto de vista de um pássaro, sistematiza o conhecimento e combina diferentes áreas do conhecimento.
- Pesadelo - para os fortes de espírito, o nível de mehmat, para os amantes da matemática e das torres de marfim.
Roteiro
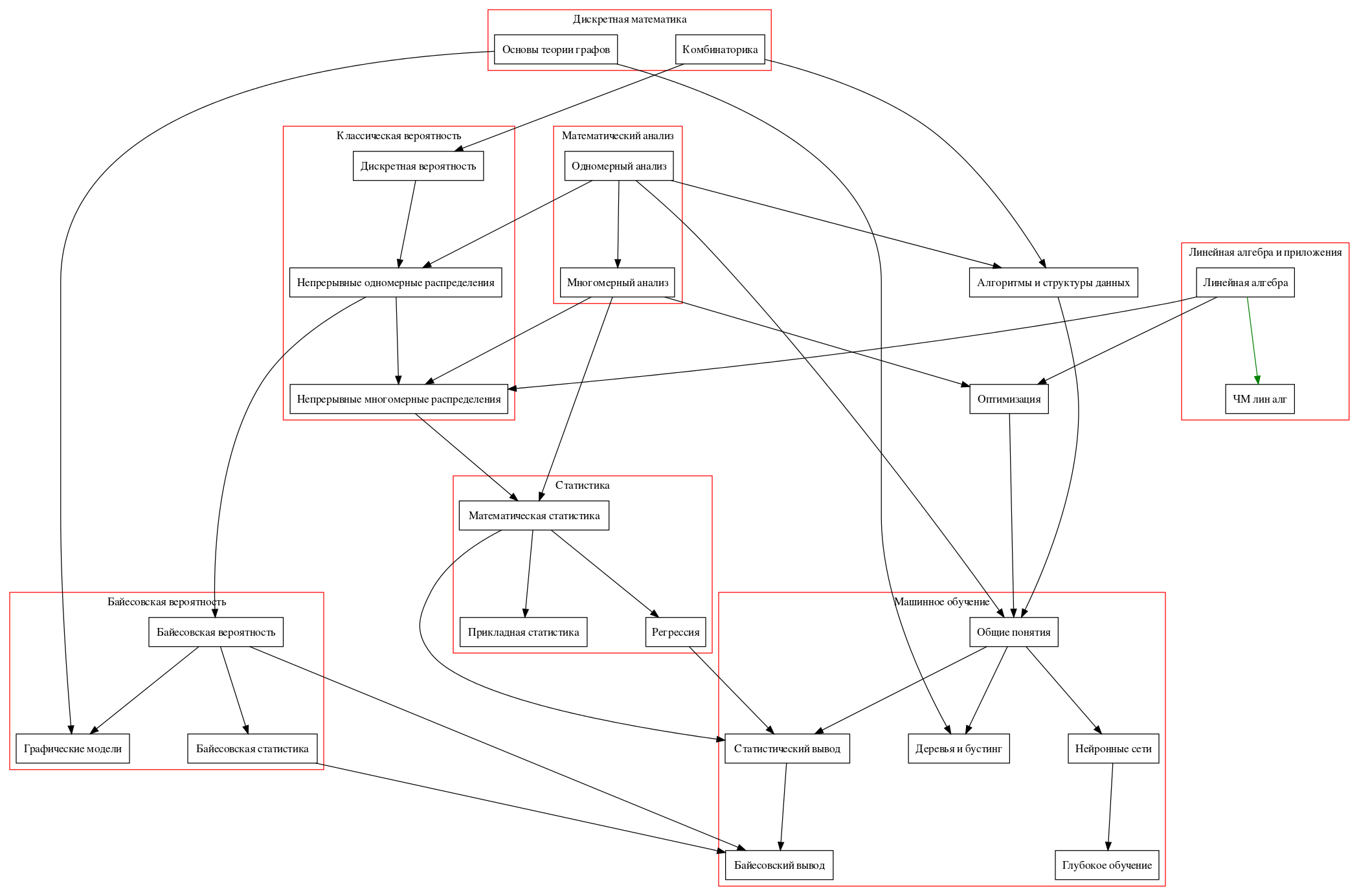
Na verdade, vou passar para cursos específicos.
Análise, ele é cálculo
Ele é ensinado de maneira bastante interessante nas universidades russas: a maioria delas, vários anos após o término do curso, lembra vagamente apenas algumas integrais por lá, e outra coisa parece estar. E isso apesar do fato de a análise ser uma disciplina, de fato, uma das fundamentais da matemática em geral. Como regra, não existem pontes da teoria para a prática, e esse curso, como uma ilha voadora, paira em algum lugar na cabeça, completamente divorciado da vida real. É necessário superar isso resolvendo problemas, além disso, não apenas do campo da matemática, mas também algo da "vida real" é desejável.
O que você precisa saber da análise?
As principais coisas que precisaremos são os conceitos de limite, continuidade, derivada, função de muitas variáveis, gradiente, integral, integral com limite superior variável, integral multidimensional *.
Literatura
Vamos lá : tudo aqui é mais ou menos padrão -
Piskunov / Fichtenholtz .
Me machuque bastante :
Zorich, Volume 1 . Eu amo muito este livro; este não é um livro, mas um romance de fórmulas, algo como Eugene Onegin. Infelizmente, é mais complicado do que os cursos de análise padrão, devido ao fato de que muitas coisas são dadas de maneira mais geral e você precisa se acostumar; mas, devido a essa semelhança, muitas coisas díspares estão ligadas (veja os mesmos limites na base).
Pesadelo :
Zorich Volume 1 + Volume 2, Rudin "Fundamentos da Análise Matemática", Lviv "Palestras sobre Análise Matemática", Ramanan "Cálculo Global".Em geral, o resumo aqui é o seguinte: a literatura de análise, mesmo em russo, está cheia; os livros didáticos tendem a ser puramente matemáticos. Como complemento aos livros didáticos de nível 2-3, posso aconselhar vários cursos:
Não analisei os cursos da sala de aula do MIPT sobre análise, mas, para completar, também darei:
Prática
Praticar e aplicar o conhecimento adquirido não é apenas “opcional”, mas estritamente obrigatório; caso contrário, toda a teoria se apoiará em você com um peso morto e você rapidamente mergulhará no fundo sem nem mesmo perceber.
Proponho considerar as seguintes opções:
Demidovich, conjuntos de problemas dos cursos do MIT (https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/index.htm)
Álgebra linear
Pão diário para a Ciência de Dados e para a ciência em geral. Infelizmente, as pessoas aprenderam a resolver bem apenas equações lineares e seus sistemas; para equações de grau 2 e acima, existem todos os tipos de teorias não triviais (álgebra comutativa, geometria algébrica e outras semelhantes). Portanto, na análise dos dados, os modelos lineares são usados principalmente (ou modelos lineares generalizados, como regressões logísticas, perceptrons etc.).
Existem muitos livros sobre álgebra linear em russo. O problema é que eles foram escritos para matemáticos, ou existem muitos índices deprimente (e não há floresta visível atrás das árvores). Muitas vezes, a ênfase nos cursos universitários está no formulário da Jordânia; outros formulários padrão geralmente não são mencionados; há Gauss e Kramer estúpido, mas raramente o que acontece sobre LU, sobre SVD.
O que você precisa saber sobre álgebra linear?
O conceito de vetor e espaço vetorial; o conceito de operador linear; comunicação de operadores e matrizes; decomposições matriciais (LU, SVD pelo menos); autovetores e autovalores; operadores unitários ortogonais; operadores simétricos e eremitas; formas quadráticas, redução aos eixos principais.
Literatura
Vamos lá :
curso OCW-MIT de Gilbert Strang sobre álgebra linear + seu livro .
ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/index.htmO melhor deste curso é a falta de teoremas “complexos” e bastante estúpidos da álgebra linear, todos os tipos de espaços duplos, um grande número de problemas no livro, uma abordagem orientada para a prática (não “o que é isso”, mas “como calculá-lo”). Mais cursos explicativos em álgebra linear que ainda não conheci.
Me machucou bastante :
Axler “Álgebra linear bem feita”; Gelfand "Palestras sobre álgebra linear "; Curso MIPT
lectoriy.mipt.ru/course/LinearAlgebra ;
Kostrikin “Introdução à Álgebra, Parte 2”, Tyrtyshnikov “Análise de Matrizes e Álgebra Linear”.O problema com livros e cursos desse nível de complexidade é que eles são teoricamente orientados. Existem funcionais lineares e espaços duplos, mas não há matriz de projeção no subespaço e métodos práticos para calcular valores próprios. Muito provavelmente, os cursos desse nível terão que ser complementados com práticas fortes; por exemplo, por métodos numéricos de álgebra linear.
Sobre o último livro separadamente. Na minha opinião, este é um dos livros de álgebra linear mais bem-sucedidos do idioma russo no sentido de que não é muito divorciado da prática; ao mesmo tempo, contém todos os tipos de tópicos "avançados". Até certo ponto, ele pode substituir completamente as palestras de Strang, mas precisa ser complementado com tarefas simples para "encher sua mão". Existem problemas neste livro, mas eles são bastante graves.
Pesadelo :
Kostrikin-Manin "Álgebra e Geometria Linear", Shafarevich-Remizov "Álgebra e Geometria Linear".Em geral, há muita literatura boa em russo, especialmente no último nível, mas sofre de complexidade excessiva.
Prática
Como no primeiro caso, é necessária prática. Vá SVD - Aprenda compressão de imagem. Passe por multiplicações de matrizes - aprenda a transformação rápida de Fourier, o algoritmo de Strassen; resolver muitos problemas (por exemplo, nos
livros de problemas de Kostrikin ou Proskuryakov ); escreva sua decomposição da LU, Gauss. Para os mais persistentes, posso oferecer livros maravilhosos sobre métodos numéricos de álgebra linear, como
Trefethen, Bau "ALGEBRA LINEAR NUMÉRICA"; Horn, Johnson "Matrix Analysis" . Esses livros serão úteis, antes de tudo, para "encher" as mãos; segundo, ficará imediatamente claro que muitos métodos teóricos são divididos em chips sobre a prosa da vida (precisão da máquina, instabilidade dos métodos, trabalho com matrizes esparsas).
Matemática discreta
Outra baleia do CS moderno. Aqui estamos interessados principalmente na combinatória e no básico da teoria dos grafos.
O que você precisa saber sobre combinatória e teoria dos grafos?
Coeficientes binomiais, seus assintóticos; gráficos; árvores; pesquisa de profundidade e largura; relações de recorrência e suas soluções;
Literatura
Vamos lá :
Anderson J. "Matemática Discreta e Combinatória"; Haggarti, Schlipf J., Whitesides S. "Matemática discreta para programadores", Ore O. "Gráficos e sua aplicação" .
Os dois primeiros livros - excelentes Talmuds em matemática discreta, cobrem quase todas as perguntas que você precisa saber.
Me machucou bastante :
Graham, Knut, Patashnik "Concrete Mathematics", Harari "Graph Theory", Minério "Graph Theory".Pesadelo :
Sachkov "Introdução aos métodos combinatórios de matemática discreta", Omelchenko "Teoria dos grafos".Prática
Como regra, um grande número de problemas está incluído nos livros didáticos sobre combinatória; eles devem ser resolvidos. De fato, toda combinatória é a arte de resolver vários problemas, em vez de uma teoria única.