Teoria da felicidade. Vôo vertiginoso de um sanduíche com manteiga

Continuo familiarizando os leitores de Habr com os capítulos de seu livro "Theory of Happiness", com o subtítulo "Fundamentos matemáticos das leis da maldade". Este livro científico ainda não foi publicado, informando de maneira muito informal sobre como a matemática permite que você olhe para a vida do mundo e das pessoas com um novo grau de conscientização. É para aqueles que estão interessados ​​em ciência e para aqueles que estão interessados ​​na vida. E como nossa vida é complexa e, em geral, imprevisível, a ênfase no livro está principalmente na teoria das probabilidades e nas estatísticas matemáticas. Aqui os teoremas não são provados e os fundamentos da ciência não são dados; isso não é de forma alguma um livro, mas o que é chamado de ciência recreativa. Mas é exatamente uma abordagem quase lúdica que nos permite desenvolver a intuição, animar as palestras para os alunos com exemplos vívidos e, finalmente, explicar aos não matemáticos e nossos filhos que encontramos coisas tão interessantes em nossa ciência seca.



Neste capítulo, examinamos a lei de um sanduíche e organizamos um estudo completo usando o método de Monte Carlo e a análise dimensional. E, finalmente, desmerecer o mito popular de que o petróleo é a causa dessa lei da maldade.

O tema da queda de sanduíches não assombra o público em geral nem os pesquisadores. Por décadas, experimentos foram realizados, filmes foram rodados, artigos escritos, um sanduíche caindo cheio de lendas e conclusões incorretas. Poucas tarefas inúteis atraíram tanta atenção e, se você acha que tudo isso é mimo, lembre-se de que mesmo os prêmios são, no entanto, também não sérios, por sua solução. Em 1995, Robert Matthews recebeu o Prêmio Shnobel por seu trabalho, "Sanduíche de queda, lei de Murphy e constantes fundamentais", publicado no European Journal of Physics. Apesar do tópico cômico e da reação correspondente da comunidade científica, este é um artigo completamente interessante, no qual é realizada uma análise aprofundada do processo de deslizamento e é feita uma conclusão abrangente: não importa em que criaturas antropomórficas que vivem na atmosfera apareçam, elas estarão condenadas à lei de um sanduíche. Após um triunfo tão inútil de pesquisa, pode-se encerrar o tópico, mas por que perder a oportunidade de considerar métodos interessantes e objetivamente úteis como exemplo de um problema interessante!

Ida jogar sanduíches em Monte Carlo!

Raramente jogamos sanduíches como uma moeda, pelo menos quando temos mais de dois anos. Frequentemente, repetimos involuntariamente o mesmo experimento: um sanduíche, originalmente colocado com a manteiga para cima, escorrega de nossas mãos ou desliza da mesa. No processo de escorregar, ele torce, voa no ar e, finalmente, cai sobre a mesa ou no chão. O estágio inicial da queda é afetado por vários parâmetros: atrito contra os dedos ou a superfície da mesa, a posição inicial do sanduíche e sua velocidade inicial, a altura da queda e, finalmente, o tamanho do sanduíche. Temos um sistema dinâmico com vários parâmetros de entrada e uma saída - a posição do sanduíche no chão. Dentro do sistema, como no caso de uma moeda, as leis mecânicas funcionam, que são descritas por equações diferenciais e são determinísticas . Isso significa que não há acidente neles - o resultado depende apenas dos dados de entrada e, com a repetição exata dos parâmetros, devemos obter resultados idênticos. Isso se aplica ao modelo de sanduíche, apresentado na forma de um sistema de equações diferenciais, mas e os sanduíches reais, brutos e únicos, descartados por pessoas reais em restaurantes, na rua ou no sofá? A variabilidade do mundo real pode ser descrita aplicando parâmetros aleatórios à entrada do sistema determinístico.

No entanto, mesmo a álgebra de variáveis ​​aleatórias, que inclui apenas adição e multiplicação, não é uma tarefa fácil, mas temos equações diferenciais! Não escalamos essas áreas selvagens fascinantes, mas usamos a técnica bem desenvolvida em muitas áreas - o método Monte Carlo . Consiste na acumulação de estatísticas e na determinação das propriedades de um determinado sistema complexo como resultado de testes repetidos com vários parâmetros aleatórios. Enfatizo novamente: o sistema em estudo não é estocástico nem caótico, e reage previsivelmente a dados de entrada aleatórios. No método de Monte Carlo, a aleatoriedade é necessária apenas para classificar com eficiência o maior número possível de opções e analisar todos os ângulos realistas, obtendo uma idéia do comportamento do sistema.

De fato, já usamos esse método, observando ciclistas em uma colina e ainda o utilizamos, estabelecendo um prazo no escritório e compartilhando dinheiro em uma sociedade fechada. A correspondência individual entre probabilidade e a medida de volume ou área, sobre a qual falamos anteriormente, nos permite usar o método de Monte Carlo para integração numérica. Uma característica do próximo experimento sanduíche é que estaremos interessados ​​não na distribuição de probabilidade (exata ou empírica), mas na dependência da probabilidade dos parâmetros do problema. Procuraremos a resposta para a pergunta: em que circunstâncias a lei sanduíche é cumprida? Forneceremos vários parâmetros específicos para a entrada do nosso sistema dinâmico e coletaremos estatísticas sobre a queda e queda de óleo. Assim, o resultado de uma série de experimentos será um número - a probabilidade de um óleo cair.

Estou convencido de que jogar deliberadamente sanduíches reais no chão está errado, então usaremos modelagem matemática. Para resolver o problema de um sanduíche caindo, escolhi um dos simuladores de mundo físico disponíveis que são usados ​​para criar jogos online. Ele permitiu criar uma mesa virtual e um piso, além de dois sanduíches. Um apareceu na beira da mesa e o segundo - "escorregou dos dedos", isto é, escorregou de um suporte pontual. É meu poder definir a posição e o ângulo inicial do sanduíche, a velocidade horizontal (o caso de esmagar o sanduíche da mesa), os coeficientes de atrito, o tamanho do sanduíche e a altura da queda. As experiências são mais ou menos assim:

Experimentos com a queda de sanduíches virtuais em um simulador do mundo físico.

No momento em que o sanduíche toca o chão, o ângulo do sanduíche é fixo, ou melhor, o ângulo do vetor normal para ele. O sinal do seno desse ângulo nos dirá de que lado o óleo saiu: um caso bem-sucedido corresponde a um valor positivo e uma posição descendente corresponde a um valor negativo. O resultado é inserido na tabela e o novo sanduíche virtual está pronto para cair. A tarefa que estabelecemos é a seguinte: avaliar a probabilidade de um sanduíche cair óleo quando cai de uma determinada altura.

O método Monte Carlo assume que variáveis ​​aleatórias são usadas como parâmetros. E aqui vale a pena dizer algumas palavras sobre o que é uma variável aleatória . Vamos voltar aos matemáticos e estruturas matemáticas. Que estrutura pode ser usada para simular os resultados da queda de um número em um dado ou do nível da água em um rio, porque há uma excitação constante na água? Como trabalhar com o número de carros que passam pelo cruzamento em uma hora? Que estrutura pode descrever o estado de um elétron? Por um lado, são números específicos de um conjunto de valores bem definido: para um osso, por exemplo, de um conjunto $$$\ {1,2,3,4,5,6 \}$ , e é fácil obter esse valor realizando uma experiência. No entanto, um segundo experimento dará um resultado diferente, esse claramente não é apenas um número: hoje é um, amanhã é outro. Uma questão filosófica pode até surgir: faz sentido falar sobre algum valor exato do "nível da água no rio" ou o número de carros, porque esses valores não podem ser "capturados" e registrados? Poderia haver, de algum modo, conhecimento exato de uma variável aleatória?

Freqüentemente, ao falar sobre essas variáveis ​​aleatórias, elas são limitadas apenas ao valor médio, mas essa é uma ótima maneira de ficar confuso ou até intencionalmente confuso. Dois números: a média e o desvio padrão, já são melhores, mas essas claramente não são todas as informações sobre o objeto de interesse para nós. Talvez estes não sejam números, mas conjuntos? Digamos, você pode tentar descrever o nível da água no rio como um intervalo de valores possíveis, levando em consideração a excitação e, por exemplo, com carros, diga que de 1 a 100 carros passam em uma hora, etc. Mas é fácil ver que o conjunto de valores possíveis também não é suficiente, por exemplo, com repetidas repetições da medição do número de carros na rua, alguns números ocorrerão com mais frequência e outros não esperaremos. No último capítulo, introduzimos uma medida de probabilidade como uma função em um espaço de probabilidade. Para uma quantidade aleatória, os eventos elementares desse espaço serão os elementos do seu domínio de definição e a medida determina a distribuição de probabilidade para essa quantidade. E agora essas são informações exaustivas e precisas. Uma função pode ser representada analiticamente ou como uma aproximação por outra função, na forma de uma tabela, um histograma ou na forma de um gráfico. Todas essas representações são modelos do mesmo objeto - uma variável aleatória, e a coisa mais importante aqui não é tanto o tipo específico de representação quanto as propriedades matemáticas dessa função. Para distribuições de probabilidade, as propriedades são diferentes: número de parâmetros, número de modos, entropia, divisibilidade infinita, aditividade, estabilidade, integrabilidade e assim por diante. Modelando uma variável aleatória desconhecida obtida a partir do experimento, os estatísticos de um enorme arsenal de distribuições conhecidas com propriedades definidas com precisão, escolhem não tanto a função “mais semelhante” como uma função que coincide mais completamente nas propriedades com a variável aleatória observada. Essa é a essência da análise estatística e das técnicas para testar hipóteses estatísticas familiares a todos os alunos que tocaram em estatística.

Agora temos um problema, em certo sentido, o oposto. Precisamos definir os parâmetros do sanduíche com variáveis ​​aleatórias, não tendo dados estatísticos, mas guiados pelas propriedades necessárias dessas quantidades. Esta é uma parte importante e interessante do método Monte Carlo, da qual dependem a solução e sua correção.

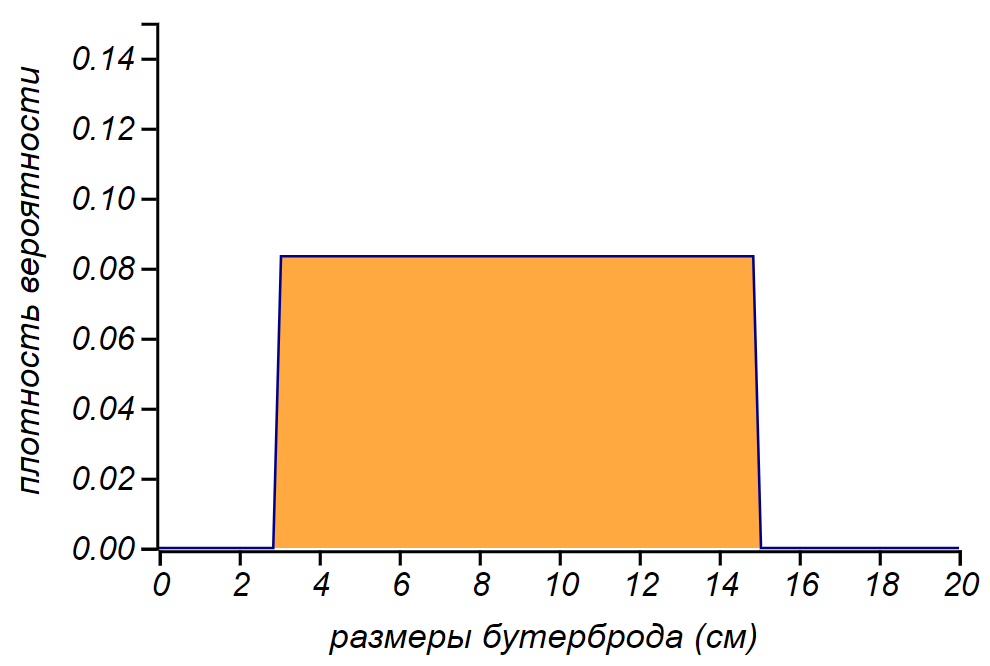1. As dimensões do sanduíche. O que eles podem ser? Canapés de tamanho razoável tem um centímetro $$$3$ largura, e um bom aluno "bast" pode ter centímetros $$$15$ . Na maioria das vezes, os sanduíches têm tamanhos de $$$6$ antes $$$10$ Neste caso, a probabilidade de encontrar um sanduíche de milímetro ou largura de metro, no sentido prático, é zero. Não posso dizer mais nada sobre sanduíches e aceitarei o tamanho dos sanduíches distribuídos igualmente no intervalo especificado. A escolha é imperfeita, no entanto, encontramos sanduíches normais com mais frequência do que pequenos ou gigantes. Mais tarde, porém, veremos que esse ponto fraco pode ser contornado com graça.

2. Posição inicial. Aqui, sem mais delongas, definiremos uma distribuição uniforme para mover o sanduíche sobre a borda da mesa, se ele cair.

3. O coeficiente de atrito. Essa é uma quantidade adimensional, dependendo apenas do material. Mesas e toalhas de mesa são diferentes, os dedos apertam um sanduíche com forças diferentes. Faixa de coeficiente de $$$0,01$ antes $$$0,5$ , embora valores extremos sejam improváveis, em média, você pode esperar algo em torno $$$0,3$ . Qualquer distribuição assimétrica em forma de sino de um valor não negativo, por exemplo, uma distribuição gama ou um log-normal, nos ajudará.

4. velocidade inicial. Raramente lançamos sanduíches em alta velocidade e, na maioria das vezes, não os jogamos, mas acontece. Tudo o que se sabe sobre a magnitude da velocidade é que ela é positiva e pode-se presumir que, ao passar, em média, nos movemos como mãos comuns, ou seja, a uma velocidade de aproximadamente $$$0,5$ m / s Se apenas isso é conhecido sobre uma quantidade, é razoável descrevê-la por uma distribuição exponencial (por que falaremos mais tarde quando aprendermos sobre a entropia das distribuições). Seu modo é zero, portanto a proporção de sanduíches que caíram sem uma grande velocidade inicial será bastante decente. No "rabo" haverá sanduíches, lançados inadvertidamente em vôo ao bater migalhas da mesa.

5. Fixaremos a altura da mesa, derrubaremos uma centena de sanduíches, contaremos o número de óleo caído e colocá-lo na mesa, ou refletiremos a probabilidade da altura no gráfico.

Aqui estão as probabilidades de deixar cair um sanduíche com manteiga:

A probabilidade de sanduíches de óleo desembarcarem sanduíches diferentes com diferentes condições, dependendo da altura da queda. Para cada altura $$$100$ testes.

Alguma tendência é visível, mas uma disseminação muito ampla acabou. Ao calcular a média, verifica-se que a probabilidade da altura de queda é quase independente e dificilmente excede a metade. Você pode confiar em tal experimento? Ele refuta a lei de um sanduíche? Talvez não tenhamos jogado sanduíches o suficiente - havia muitos dados barulhentos! Vamos aumentar o número de jogadas e ver o que acontece:

A probabilidade de um óleo pousar em vários sanduíches calculada para um número maior de testes (500 para cada altura).

Há menos emissões, mas é ainda mais claramente visível que a lei do sanduíche é muito, muito fraca. Mas realizamos nossos experimentos corretamente? O método Monte Carlo parece tentadoramente simples: conheça você mesmo, substitua os dados horríveis e veja o que acontece. A matemática é uma coisa honesta: que tipo de pergunta ela está pronta para dar que tipo de resposta . Mas se essa resposta faz sentido depende da pergunta.

Antes de iniciar as experiências, não tão parecidas com brinquedos quanto as nossas, mas reais e caras, usando um satélite em órbita, um acelerador de partículas ou mil sanduíches reais com óleo, é necessário realizar trabalhos preparatórios. E uma das maneiras poderosas e bonitas de entender como conduzir um experimento corretamente é analisar as dimensões do problema.

Modelamos um sanduíche por coordenadas generalizadas, momentos e forças - quantidades físicas que, por sua vez, são conectadas por equações da mecânica analítica. Na física, as quantidades quantitativas com as quais lidamos, que medimos e substituímos nas equações, não "se encaixam" em números comuns - elas têm uma estrutura adicional, chamada dimensão . Nem todas as expressões matemáticas corretas fazem sentido se quantidades dimensionais participarem delas. Digamos que não faça sentido adicionar velocidade e massa, é impossível comparar força e distância. Contudo, podemos considerar o produto da velocidade e da massa, tendo recebido uma nova quantidade dimensional - o momento ou momento; é possível quadrar a velocidade e dividir pela distância, obtendo-se assim um valor com a dimensão de aceleração.

A análise de dimensões e a teoria da similaridade nasceram há muito tempo, desde a época de Lord Rayleigh. Eles são usados ​​em mecânica, eletrodinâmica, astrofísica e cosmologia, tornando possível abordar tarefas complexas com uma elegância assustadora. No entanto, as pesquisas nesta área não foram concluídas e uma definição rigorosa da estrutura formada por quantidades quantitativas (dimensionais) foi dada apenas em 2016 pelo matemático espanhol Alvaro Raposo.

As restrições impostas pelas dimensões nas fórmulas físicas são frequentemente percebidas por alunos e alunos como uma bagunça extra que precisa ser monitorada. Mas, por outro lado, restrições logicamente consistentes são extremamente úteis! Eles filtram expressões incorretas, permitem "prever" a estrutura da solução de um problema físico antes de sua solução detalhada, são uma ferramenta poderosa no planejamento e análise de dados experimentais.

Mas isso é interessante. Calculamos a queda do sanduíche no programa, usando números não dimensionais, mas comuns. Como alguém pode "limpar" uma quantidade física de uma dimensão e transformá-la em um número? Para esse fim, estamos familiarizados com as unidades familiares de medida de grandezas físicas: todos esses medidores, libras, minutos e Newtons. As unidades de medida assumem a parte dimensional da quantidade, deixando-nos com um fator - um número real, com o qual um computador já pode lidar. Por exemplo, a velocidade na direção selecionada é $$$60$ km / h pode ser representado pelo número $$$60$ . Mas há uma sutileza: a representação numérica depende da escolha das unidades de medida. Se você selecionar outras unidades (por exemplo, metros e segundos) , a mesma velocidade será representada por um número diferente: $$$16,7$ . Os números são diferentes, mas a quantidade é um e não depende da escolha de nenhuma unidade.

Surge a questão: existe em algum sentido um “melhor” sistema de unidades? Acontece que, para isso, ao resolver o problema, é necessário usar as quantidades dimensionais incluídas no problema como unidades de medida.

Neste capítulo, temos sanduíches voando; nas moedas voadoras anteriores, damos mais um exemplo de vôo. Como as qualidades de vôo de diferentes aves devem ser comparadas? É claro que as velocidades que os pássaros desenvolvem são diferentes: para um pombo - $$$90$ km / h, rapidamente $$$140$ km / h, para guindastes, pardais ou marrecos - $$$50$ km / h, beija-flor - $$$80$km / h Mas todas essas aves variam significativamente em tamanho e maneira de voar. Se o comprimento de um papagaio é medido em papagaios, e o tempo é medido em períodos de bater as asas, você pode obter uma velocidade própria , como eles dizem . Você pode dividir as velocidades que essas aves podem desenvolver em autovalores e obter uma velocidade sem dimensão que mostra quanto tempo a ave pode viajar com um único toque de asas. Aqui está o resultado dessa comparação:

o passarinho	velocidade, km / h	comprimento do corpo	frequência de varredura, 1 / s	velocidade própria, m / s	velocidade adimensional
rápido	140	18 cm	5	0,9	43
pombo-correio	90	30 cm	5	1,5	17
beija-flor	80	8 cm	200	16	1.4
guindaste	50.	1 m	2,5	2,5	5
pato-real	50.	40 cm	9	3.6.	3.8
pardal	46.	12 cm	13	1,6	8

Pode-se ver que o veloz é justamente considerado o melhor passageiro, mas o beija-flor consome ineficientemente energia, no entanto, esse pássaro não tem a tarefa de voar por um longo tempo, como uma pomba. As mesmas velocidades absolutas do guindaste, pardal e pato diferem significativamente quando traduzidas em quantidades sem dimensões. Esse tipo de cálculo é usado para simular uma aeronave real de grande porte, testando um pequeno modelo em um túnel de vento. Se todos os parâmetros adimensionais desses dois sistemas estiverem próximos, eles podem ser considerados fisicamente semelhantes e a modelagem faz sentido. Já usamos essa abordagem, refletindo unidades relativas em vez de absolutas nos diagramas de Lorenz. Isso nos permitiu comparar entre si vários fenômenos e distribuições.

Está claro qual será o sistema de unidades mais adequado ao analisar o voo de um sanduíche. Obviamente, o comprimento deve ser medido em sanduíches. Por uma unidade de tempo, podemos pegar o valor$$$\sqrt{l/g}$ onde $$$l$ - o comprimento do sanduíche, e $$$g$- aceleração da gravidade. E a altura da mesa não deve ser medida em metros, mas em suas próprias unidades. Tendo assim obtido o resultado, podemos generalizá-lo imediatamente, tanto no caso dos canapés quanto em um sólido "sapato". Então, repetimos os cálculos, mas no gráfico refletimos a altura da tabela em unidades relativas. Se fizermos tudo certo, então, para dois sanduíches de tamanhos diferentes, devemos obter gráficos muito semelhantes. Vamos verificar isso:

A probabilidade de um sanduíche de óleo atingir um determinado valor fixo, em diferentes alturas de incidência, calculada em unidades relativas. Pontos azuis correspondem a um sanduíche com tamanho de 5 cm, pontos vermelhos correspondem a 10 cm.

Na formulação inicial, classificamos vários tamanhos e recebemos uma nuvem de resultados nos quais a dependência de nosso interesse estava oculta. Com um aumento no número de testes, calculamos a média dessa nuvem e recebemos uma resposta desinteressante. Para mostrar com mais clareza em que consistia o erro metodológico, imagine que desejamos calcular a probabilidade de um sanduíche cair de manteiga, observando aleatoriamente as condições e tamanhos iniciais do sanduíche e da altura. Isso é equivalente à média de todos os resultados que obtivemos de uma só vez. Como resultado, obtemos um meio termo confiante - uma probabilidade muito próxima de$$$1/2$como jogar uma moeda! Este é um resultado muito lógico e esperado, mas é completamente desinteressante. Ao calcular a média de muitos dados para tamanhos diferentes, já estamos perto dessa conclusão. Mas se o objetivo da modelagem é identificar padrões, faz sentido minimizar o número de parâmetros.

Os dados limpos agora falam claramente a favor da lei da maldade, limitando-a, no entanto, a uma certa faixa de altura: de$$$2$ antes $$$6$ o tamanho do sanduíche (da altura do cotovelo acima da mesa à altura dos braços de uma pessoa em pé). Fora desse intervalo, o sanduíche tem uma chance maior de virar o lado direito antes de cair.

Mas e se você olhar mais longe e jogar sanduíches pela janela? É claro que ao cair de uma grande altura, não importa de que lado ele caia no que o sanduíche se tornará, e a resistência do ar estabiliza a queda, mas teoricamente, o que esperamos ver? Provavelmente, algumas flutuações de probabilidade devem ser observadas à medida que o tempo de voo aumenta. Vamos ver:
A probabilidade de um sanduíche de óleo pousar ao cair de uma altura alta.

Adivinhámos com a frequência, mas é curioso que a amplitude diminua e as flutuações da probabilidade converjam em $$$0,5$ . Sobre o que isso pode falar? É o mesmo efeito que no caso de uma moeda, quando, com o aumento da duração do voo, as consequências dos desvios das condições iniciais se tornam mais significativas? Acontece que, neste caso, a natureza da equalização de probabilidades é diferente.

Um pouco mais de análise dimensional

Por mais frívolo que seja o tópico de nosso livro, falamos a linguagem da matemática e ele se esforça para encontrar soluções exatas. O método de Monte Carlo nos permitiu ter uma idéia da solução, mas era o que se chama força bruta. Isso não é tão interessante quanto pelo menos alguns, mas uma solução analítica. Uma análise das dimensões nos permitirá obter uma forma teórica da dependência obtida pelo método de Monte Carlo. Para isso, não precisamos resolver equações diferenciais; além disso, todas as nossas considerações não vão além dos limites de relações completamente primitivas e óbvias. Esse é o charme da análise dimensional, que às vezes parece um truque. Então, vamos começar, restringindo-nos por uma questão de simplicidade, apenas colocando um sanduíche de comprimento $$$l$ da tabela de altura $$$H$ com velocidade horizontal zero.

1. O ângulo de rotação do sanduíche em queda depende do tempo e da velocidade angular:

$$

$$\ varphi = t \ ômega.$$

2. A velocidade angular é igual ao produto do tempo de deslizamento e da aceleração angular:

$$

$$\ omega = t_0 \ varepsilon.$$

3. O tempo de deslizamento pode ser expresso em termos da aceleração da gravidade e parte do comprimento do sanduíche que entrou em contato com a tabela na seguinte proporção:

$$

$$t_0 \ propto \ sqrt {\ frac {l_0} {g}}.$$

Aqui $$$l_0$ - o comprimento do sanduíche deitado sobre a mesa. Aqui usamos a relação de proporcionalidade indicada pelo sinal $$$\ propto$ . Expressão $$$y \ propto x$ pode ser substituído por $$$y = C x$ onde $$$C$ - alguma constante desconhecida. Eu realmente amo essa atitude. A proporcionalidade “incorpora” tudo o que é complicado, que se transforma em constante: tanto o fato de o momento da gravidade mudar durante a rotação quanto o centro de rotação ao deslizar. Tudo isso, é claro, você precisa saber para um cálculo preciso, mas o resultado é apenas um coeficiente sem dimensão e, em nossa análise, ele não desempenha um papel. Com um ícone, nos salvamos da integração tediosa.

4. A aceleração angular ocorre a partir da aceleração da gravidade e depende do ombro ao qual a gravidade é aplicada:

$$

$$\ varepsilon \ propto \ frac {g} {l-l_0}.$$

E novamente o sinal $$$\ propto$ nos permitiu não calcular o momento de inércia da placa para o eixo que está no seu plano, bem como a mudança na projeção da gravidade (essas são mais duas integrais).

5. Finalmente, o tempo de queda depende da altura da mesa e da aceleração da gravidade:

$$

$$t \ propto \ sqrt {\ frac {H} {g}}.$$

6. Substituindo todas essas expressões na primeira fórmula, obtemos um resultado simples:

$$

$$\ varphi \ propto \ sqrt {\ frac {l_0 H} {l (l-l_0)}},$$

que, se você medir todos os comprimentos dos sanduíches, se transforma em

$$

$$\ varphi \ propto \ sqrt {\ frac {x h} {1-x}}.$$

Aqui $$$l_0 = x l$ e $$$H = h l$ . Bem, tudo converge - o ângulo é adimensional e depende de coeficientes adimensionais. Esse ângulo não depende da escala de tempo; a geometria pura permanece. O denominador não é perigoso quando $$$x> 0,5$ o sanduíche não cairá (estamos considerando a velocidade horizontal zero), então $$$0 <x <0,5$ .

De que lado o sanduíche cairá é determinado pelo sinal do seno do ângulo $$$\ varphi$ ou seja, função $$$\ mathrm {sinal} (\ sin \ varphi)$ . Esta função retorna $$$-1$ para o caso de "óleo para cima" e $$$1$ para "óleo para baixo". Podemos usar essa função para expressar a probabilidade de um sanduíche determinístico cair se o levarmos a uma faixa de $$$0$ antes $$$1$ :

$$

$$P _ {\ downarrow} (x, h) = \ frac12 \ left [1+ \ mathrm {sinal} (\ sin \ varphi) \ right] = \ frac12 \ left \ {1+ \ mathrm {sinal} \ left [ \ sin \ left (C \ sqrt {\ frac {xh} {1-x}} \ right) \ right] \ right \},$$

onde a seta indica simbolicamente a posição do óleo. Coeficiente $$$C$ que aparece na fórmula de probabilidade expressa tudo o que permanece oculto com a ajuda do sinal proporcional. Foi realmente uma jogada muito complicada, que nos salvou da integração tediosa (e até três), mas como descobrimos agora a que esse coeficiente é igual? Além disso, a partir da experiência, uma única experiência com a medição do ângulo no momento da queda é suficiente para obter uma estimativa desse valor! Usando o simulador, descobri facilmente que $$$C = 2,3$ .

A próxima tarefa é expressar matematicamente quais são as posições iniciais $$$x$ pode ser diferente. Estamos interessados ​​na probabilidade de um sanduíche cair manteiga se $$$x$ será igual $$ ou $$ ou qualquer número de $$$0$ antes $$$0,5$ . Usamos a união "ou", e cada um desses casos é considerado por nós independente e excluindo todos os outros em um experimento específico. Lembre-se de que probabilidade é uma medida do espaço de probabilidade e, nesse caso, a probabilidade é aditiva. Isso nos permite simplesmente adicionar as probabilidades $$$P _ {\ downarrow} (x, h)$ , para todos os valores $$$x$ , multiplicando-se anteriormente pela probabilidade de cair em um intervalo específico de valores. Nós separamos o segmento de $$$0$ antes $$$0,5$ em $$$n$ partes e calcule a estimativa de probabilidade na forma de uma soma:

$$

$$P _ {\ downarrow} (h) \ sim \ frac {2} {n} \ soma \ limites_ {i = 0} ^ n P _ {\ downarrow} \ left (\ frac {i} {2n}, h \ right ),$$

aqui está o multiplicador $$$2 / n$ expressa probabilidade para uma variável aleatória $$$x$ entrar em um pedaço de largura $$$1 / n$ . Veja como é o resultado para um número significativo de partições ( $$$n = 100$ ) e uma série de experiências numéricas com velocidade horizontal zero:

Avaliação teórica e experimental da probabilidade de um óleo pousar em um sanduíche quando ele cai de uma grande altura. A velocidade horizontal inicial nos experimentos é zero.

A solução que apresentamos antes contém mais parâmetros aleatórios, por isso ficou mais suave e próxima de $$$0,5$ . Mas, em princípio, a análise dimensional pode ser realizada para um caso mais geral.

Observe que a probabilidade $$$P _ {\ downarrow}$ aproximando-se com o aumento $$$h$ para valores próximos a $$$0,5$ . E isso não se deve à incerteza e influência dos erros iniciais. Os cálculos mostraram que este é o resultado da adição dos muitos harmônicos formados pelos valores $$$x$ ao somar $$$P _ {\ downarrow} (x, h)$ . Se esquecermos o infeliz sanduíche e continuarmos a programação $$$P _ {\ downarrow}$ , vemos que a estimativa de probabilidade continuará a flutuar tão perto $$$0,5$ , buscando gradualmente esse valor.

É possível descobrir sem cálculos diretos se a probabilidade continuará a convergir para $$$0,5$ ou ele voltará a crescer? E nesse fenômeno também há um lugar para a matemática não trivial e profunda. O fato é que cada valor $$$x$ uma certa frequência de oscilações corresponde e todo o conjunto forma o chamado espectro da função total. Se o espectro é discreto, isto é, consiste em frequências separadas, a função total (denominada transformação de Fourier) será periódica. Para um espectro contínuo na forma de uma constante em um segmento de $$$0$ antes $$$0,5$ uma função aperiódica correspondente a oscilações minguantes corresponderá. Mas analisamos um novo ramo da matemática - a análise funcional .

O grande Enrico Fermi, avô do método Monte Carlo (o matemático Stanislav Ulam é considerado o pai), ensinou seus alunos a fazer avaliações simples, descobrir um pedaço de papel ou dedos que esperamos obter antes de prosseguir com a solução exata para o problema. É maravilhoso que, se a avaliação estiver correta, ficará claro que a essência do problema é capturada; caso contrário, esse é o resultado mais útil - isso significa que a tarefa acabou sendo mais interessante do que parece!

No nosso caso, basta uma estimativa simples; o problema do sanduíche não vale uma solução mais completa. O método de Monte Carlo nos mostrou apenas sugestões da solução, e a análise dimensional mostrou apenas parte de sua estrutura geral, mas juntos eles poderiam nos mostrar como a probabilidade desejada funciona. A erudição permite que o matemático veja estruturas prontas nos projetos da solução e faça suposições e conclusões de longo alcance.

Robert Matthews, em seu estudo de referência, também usou a análise dimensional para mostrar que a lei do sanduíche é fundamental. Sua conclusão é baseada no fato de que a altura máxima de um organismo que atingiu seus membros posteriores com o objetivo de levar os membros anteriores para tomar um sanduíche com óleo é determinada pelas propriedades de força dos tecidos biológicos e da gravidade. Por sua vez, o tamanho característico do sanduíche deve corresponder à escala da criatura - e os anões em algum planeta pesado e as dylds em um planeta com baixa gravidade escolherão sanduíches para si mesmos em tamanho. Aqui chegamos ao que é chamado de especulação na ciência. Esta não é uma revenda de nenhum bem a preços exorbitantes, mas suposições dúbias que formam a base de uma construção lógica. Em particular, assumimos que as criaturas têm mãos com proporções semelhantes às nossas, e isso é mais do que discutível.

Sobre óleo e vento

Na merfologia, a citação incorreta da lei de X.L. Grupo Menka:

Problemas complexos sempre têm soluções simples, fáceis de entender e incorretas.

Você pode ouvir muitas vezes que a lei do sanduíche é a culpada pelo óleo, que é mais denso que o pão e, portanto, "supera". E, embora isso não se aplique ao assunto de nosso livro, quero analisar essa questão para pôr um fim nela. Para que mais tarde alguém pudesse se referir ao fato de que “os cientistas provaram que a presença de óleo não afeta de que lado o sanduíche bate!”

Quando criança, nos divertíamos jogando uma mosca de pombo ou uma pena de cauda, ​​presa em um pedaço de plasticina, com um centímetro ou dois de diâmetro, no alto. Ele voou até quatro metros, após o que desceu de maneira bonita e suave na auto-rotação, como um helicóptero com um motor abafado. Então crescemos e nossa diversão se tornou menos inofensiva. Pegamos uma porca e aparafusamos dois parafusos de lados opostos, comprimindo o recheio das cabeças de fósforo esmagadas. Restava amarrar uma fita ou apenas um pedaço de corda a um dos parafusos, destorcer adequadamente e correr no céu por quinze metros. No outono, uma fita leve estabilizou a posição vertical do projétil, proporcionando um impacto de alta qualidade no asfalto e uma pequena explosão, às vezes rasgando a porca em pedaços. (Tenha cuidado se você decidir compartilhar esta experiência de infância com seus filhos!)

Nos dois experimentos, vemos que uma caneta ou fita leve apareceu rapidamente sobre a parte pesada do aparelho e estabilizou a queda. Aparentemente, isso leva a uma opinião intuitiva de que manteiga pesada e pão leve também devem se comportar dessa maneira. Imagine um balão: uma cesta mais densa está sempre localizada sob um balão menos denso. Além disso, a experiência sugere que, se você pegar com dois dedos o meio geométrico de um objeto com uma massa assimetricamente distribuída, ele tombará para que a parte pesada fique no fundo.

Mas esses dois fenômenos não funcionam no caso de um sanduíche caindo.

Vamos começar com o segundo processo - com "superação". Não foi por acaso que eu especifiquei tediosamente: "... se você assumir o ponto médio geométrico de um objeto ...", aqui se entende que os pontos de tangência estão em uma determinada linha reta, formando o eixo de rotação que passa pelo centro de gravidade do objeto. Nesse caso, de fato, uma posição estável será aquela em que o centro de gravidade esteja abaixo do eixo. Mas se o eixo de rotação formado pelos dedos passar pelo centro de gravidade, o sistema estará em equilíbrio indiferente - ele não se importará com a orientação.

O que faz uma pena com um peso pequeno, uma bomba de uma noz ou um balão com balões em uma cesta faz você navegar da maneira "correta"? Ar. Ele "segura" nossos objetos para que o eixo passe acima do centro de gravidade. Mais precisamente, um fluxo de ar que se aproxima que cria uma força distribuída sobre a área do corpo. E o ponto condicional de aplicação dessa força estará localizado próximo ao centro geométrico do quadrado da figura. Para tornar mais claro, desenharemos as forças que atuam no balão condicional, como em um objeto com uma densidade desigual:

As forças que trazem o balão para uma posição estável.

Que tal um sanduíche?

Primeiro, se "desligarmos" o ar, ele simplesmente cairá. Em queda livre, o corpo gira precisamente em torno do centro de massa, para que não tenha motivos para se virar de maneira especial. Como se costuma dizer na escola: "Em um elevador em queda, a ausência de peso é observada". A manteiga no sanduíche é igualmente leve.

O óleo denso pode afetar o processo de escorregamento, aumentará efetivamente o centro de massa acima do toque exato e mudará a expressão para aceleração angular $$$l$ em $$$\ sqrt {l ^ 2 + d ^ 2} = l \ sqrt {1+ \ delta ^ 2}$ onde $$$\ delta = d / l$ - a espessura relativa do sanduíche. Para valores pequenos $$$\ delta$ esta expressão pode ser calculada como $$$l (1+ \ delta ^ 2/2)$ . Obtemos, como se costuma dizer, um efeito de segunda ordem. Para um sanduíche com uma proporção entre largura e espessura, como $$$5$ para $$$1$ , as mudanças relativas não excedem $$$2 \%$ . E este é o limite máximo máximo do efeito, porque elevamos o centro de massa à espessura do sanduíche, o que corresponde a um óleo infinitamente denso!

Agora ligamos o ar novamente, deixando a densidade do óleo infinitamente maior que a densidade do pão. Temos uma placa fina e densa com um pára-quedas leve, mas resistente ao ar. Enquanto o plano do sanduíche é horizontal, o momento da força do ar proporcional ao vento atua sobre ele - a área com a qual o fluxo de ar interage: $$$M _ {-} \ propto l ^ 2$ . Na posição vertical, o vento diminui e, portanto, o momento será diferente: $$$M_ {|} \ propto l d$ . A proporção destes pontos: $$$M_ {|} / M _ {-} \ propto \ delta.$ Escrevi um sinal proporcional aqui, já que os coeficientes de resistência para uma placa localizada ao longo e ao longo do fluxo são diferentes e são desconhecidos para mim. Mas eles não são necessários - já está claro que o efeito do ar na posição vertical (ou seja, torna a posição do óleo desigual) é mais fraco do que na horizontal. E agora lembramos que o sanduíche gira, o que significa que ele é substituído pelo fluxo no final ou no avião. Podemos introduzir uma medida da ação das forças de resistência. Se a velocidade angular de rotação não muda significativamente em um período (e esse é o caso do ar), faz sentido tomar como medida a mudança no momento angular proporcional à duração da força. Por sua vez, o período de ação é proporcional ao ângulo “varrido” pelo sanduíche durante esse período. Como resultado, medidas de momentos de ação $$$M_ {|}$ e $$$M _ {-}$ será proporcional $$$M_ {|} \ varphi_ {|}$ e $$$M _ {-} \ varphi _ {-}$ onde os ângulos que varrem o final e o plano são mostrados no desenho. 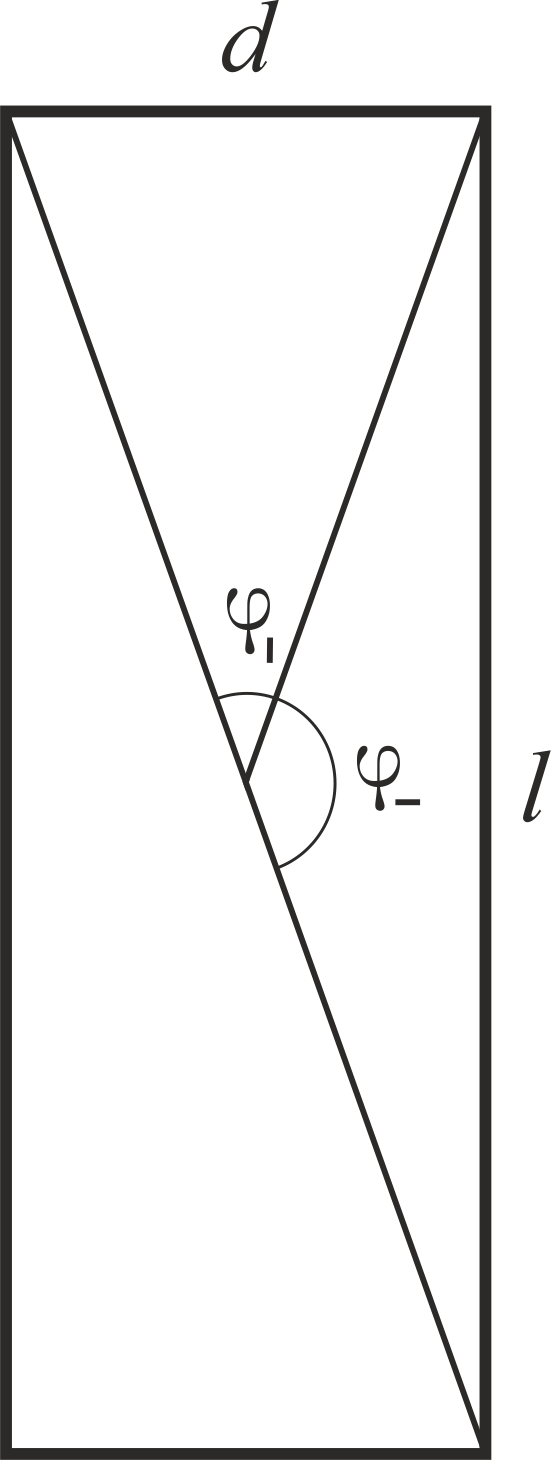Poderíamos usar o trabalho das forças de resistência como uma medida e obter a mesma proporção. A proporção do ângulo é fácil de calcular:

$$

$$\ frac {\ varphi_ {|}} {\ varphi _ {-}} = \ frac {\ varphi_ {|}} {\ frac {\ pi} {2} - \ varphi_ {|}}.$$

Em pequenas $$$d / l$ , $$$\ varphi_ {|} \ sim \ delta$ (usamos a propriedade da tangente de um pequeno ângulo $$$10 \%$ precisão em ângulos menos $$$30 ^ \ circ$ ) e, portanto, temos:

$$

$$\ frac {M_ {|} \ varphi_ {|}} {M _ {-} \ varphi _ {-}} \ sim \ delta \ frac {\ delta} {\ frac {\ pi} {2} - \ delta} \ propto \ delta ^ 2.$$

Novamente, verifica-se que o efeito da assimetria para um sanduíche plano é limitado pelo efeito de segunda ordem. Tipicamente, a densidade da manteiga é apenas o dobro da do pão, e o centro de deslocamento da massa não excede um terço da espessura do sanduíche com uma camada razoável de manteiga que não excede a espessura do pão. Esta observação reduzirá o efeito do óleo para $$$0,2 \%$ .

Se pareceu ao leitor que agora estávamos atirando nos pardais da arma, então eu concordo completamente com ele. Mas, em primeiro lugar, não quero ouvir mais sobre o petróleo "compensador", em segundo lugar, não quero ser infundado e, em terceiro lugar, queria mostrar como o físico estima as quantidades, representando o processo, mas não tendo dados completos. É claro que, no momento do pouso, a manteiga pode grudar no chão e impedir que o sanduíche pule e vire novamente, mas certamente não vou desmontar a mecânica do impacto, da deformação elástica e do salto de um pedaço de pão. Portanto, muitas análises foram feitas para esse problema. E o segundo Shnobelevskaya para ela não será mais dado.

$$

$$* * *$$

O objetivo do nosso caminho não era tão importante: a refutação ou justificação da lei do sanduíche, como o próprio caminho. Ele mostrou como a combinação de diferentes métodos matemáticos permite analisar o problema de diferentes ângulos e fornece conhecimento bastante preciso, mesmo sem uma solução detalhada para o problema. A consistência de várias disciplinas matemáticas, abordagens e pontos de vista é a força e a beleza da matemática. É apropriado relembrar as maravilhosas palavras de Marina Tsvetaeva: "Eu não quero ter um ponto de vista, quero ter uma visão" . O estudo de várias áreas da matemática pode dar ao pesquisador uma verdadeira visão multidimensional “volumétrica”, que permite que você examine o espaço aparentemente fechado e oculto do conhecimento.