Provavelmente, qualquer serviço que geralmente tenha uma pesquisa, mais cedo ou mais tarde chega à necessidade de aprender a corrigir erros nas consultas do usuário. Errare humanum est; os usuários são constantemente selados e equivocados, e a qualidade da pesquisa inevitavelmente sofre com isso - e com ela a experiência do usuário.

Além disso, cada serviço tem suas próprias especificidades, seu próprio vocabulário, que deve poder operar o corretor de erros de digitação, o que complica bastante o uso de soluções existentes. Por exemplo, essas solicitações precisavam aprender a editar nosso tutor:



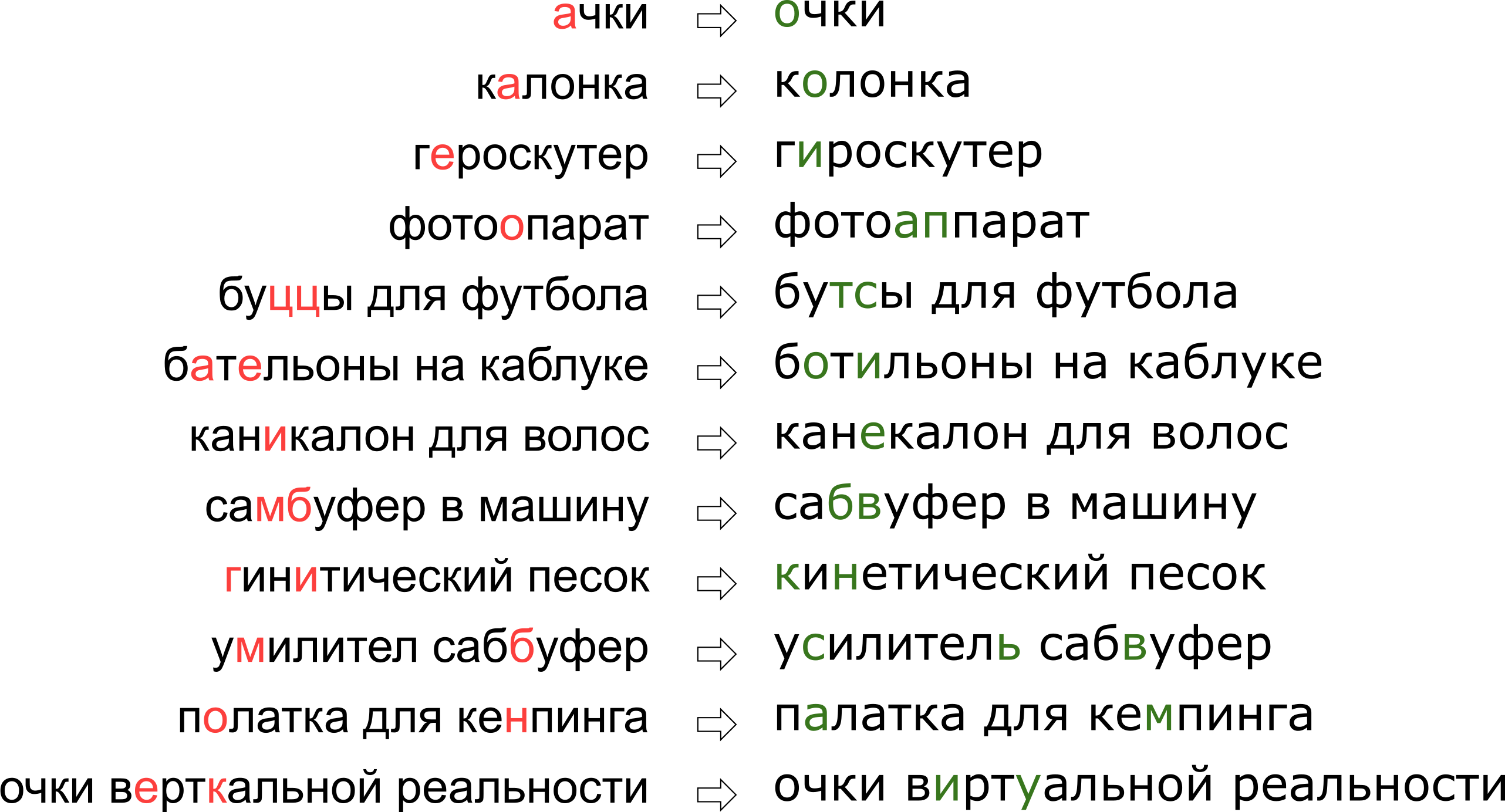Pode parecer que negamos ao usuário seu sonho de realidade vertical, mas, na verdade, a letra K simplesmente fica no teclado ao lado da letra U.

Neste artigo, examinaremos uma das abordagens clássicas para corrigir erros de digitação, desde a construção de um modelo até a escrita de código em Python e Go. E como um bônus - um vídeo do meu relatório " Óculos de realidade vertical": corrigimos erros de digitação nas consultas de pesquisa "no Highload ++.

Declaração do problema

Então, recebemos uma solicitação selada e precisamos corrigi-la. Geralmente, o problema é colocado matematicamente da seguinte maneira:

• dada a palavra $$$s$ transmitidos para nós com erros;
• tem um dicionário $$$\ Sigma$ as palavras certas;
• para todas as palavras w no dicionário existem probabilidades condicionais $$$P (w | s)$ o que se quis dizer com a palavra $$$w$ desde que tenhamos a palavra $$$s$ ;
• você precisa encontrar a palavra w no dicionário com probabilidade máxima $$$P (w | s)$ .

Essa afirmação - a mais elementar - sugere que, se recebemos uma solicitação de várias palavras, corrigimos cada palavra individualmente. Na realidade, é claro, quereremos corrigir a frase inteira como um todo, dada a compatibilidade de palavras adjacentes; Falarei sobre isso mais adiante na seção "Como corrigir frases".

Existem dois momentos pouco claros - onde obter o dicionário e como contar $$$P (w | s)$ . A primeira pergunta é considerada simples. Em 1990 [1], o dicionário foi compilado a partir do banco de dados do utilitário de feitiços e dicionários disponíveis eletronicamente; em 2009, o Google [4] simplificou e simplesmente adotou as principais palavras mais populares da Internet (junto com erros ortográficos populares). Adotei essa abordagem para construir meu tutor.

A segunda pergunta é mais complicada. Se apenas porque sua decisão geralmente começa com a aplicação da fórmula de Bayes!

$$

$$P (w | s) = \ mathrm {const} \ cdot P (s | w) \ cdot P (w)$$

Agora, em vez da probabilidade incompreensível inicial, precisamos avaliar dois novos, um pouco mais compreensíveis: $$$P (s | w)$ - a probabilidade de que, ao digitar uma palavra $$$w$ pode ser selado e obter $$$s$ e $$$P (w)$ - em princípio, a probabilidade de o usuário usar a palavra $$$w$ .

Como avaliar $$$P (s | w)$ ? Obviamente, é mais provável que o usuário confunda A com O que b com S. E se corrigirmos o texto reconhecido no documento digitalizado, há uma alta probabilidade de confusão entre rn e m. De uma forma ou de outra, precisamos de algum tipo de modelo que descreva os erros e suas probabilidades.

Esse modelo é chamado de modelo de canal barulhento (o modelo de canal barulhento; no nosso caso, o canal barulhento começa em algum lugar no centro do Brock do usuário e termina no outro lado do teclado) ou, mais brevemente, o modelo de erro é o modelo de erro. Esse modelo, discutido em uma seção separada a seguir, será responsável por levar em conta erros de ortografia e, de fato, erros de digitação.

Classifique a probabilidade de usar a palavra - $$$P (w)$ - é possível de diferentes maneiras. A opção mais simples é levar em conta a frequência com que a palavra ocorre em algum grande corpus de textos. Para o nosso tutor, levando em conta o contexto da frase, é claro, é necessário algo mais complicado - outro modelo. Esse modelo é chamado de modelo de linguagem, um modelo de linguagem.

Modelo de erro

Os primeiros modelos de erro foram considerados $$$P (s | w)$ , calculando as probabilidades de substituições elementares no conjunto de treinamento: quantas vezes em vez de E eles escreveram E, quantas vezes em vez de T escreveram T, em vez de T - T e assim por diante [1]. O resultado foi um modelo com um pequeno número de parâmetros que poderiam aprender alguns efeitos locais (por exemplo, que as pessoas frequentemente confundem E e I).

Em nossa pesquisa, adotamos um modelo de erro mais desenvolvido, proposto em 2000 por Brill e Moore [2] e reutilizado posteriormente (por exemplo, por especialistas do Google [4]). Imagine que os usuários não pensem em caracteres separados (confunda E e I, pressione K em vez de Y, pule um sinal macio), mas podem alterar trechos arbitrários de uma palavra por qualquer outra - por exemplo, substitua TSYA por TYSYA, Y por K, SHA por SHCHYA, SS para C e assim por diante. A probabilidade de o usuário ser selado e, em vez de TSYA, escrever THY, denotamos $$$P (\ texto {milhares} \ rightarrow \ texto {mil})$ É um parâmetro do nosso modelo. Se para todos os fragmentos possíveis $$$\ alpha, \ beta$ podemos contar $$$P (\ alpha \ rightarrow \ beta)$ , então a probabilidade desejada $$$P (s | w)$ um conjunto da palavra s ao tentar digitar a palavra w no modelo de Brill e Moore pode ser obtido da seguinte forma: dividimos as palavras w e s em fragmentos mais curtos de todas as maneiras possíveis, para que haja o mesmo número de fragmentos em duas palavras. Para cada partição, calculamos o produto das probabilidades de todos os fragmentos w para transformar os fragmentos correspondentes s. O máximo para todas essas partições será considerado como o valor de $$$P (s | w)$ :

$$

$$P (s | w) = \ max_ {s = \ alpha_1 \ alpha_2 \ ldots \ alpha_k, w = \ beta_1 \ beta_2 \ ldots \ beta_k} P (\ alpha_1 \ rightarrow \ beta_1) \ cdot P (\ alpha_2 \ rightarrow \ beta_2) \ cdot \ ldots \ cdot P (\ alpha_k \ rightarrow \ beta_k) \ ,.$$

Vejamos um exemplo da partição que ocorre ao calcular a probabilidade de imprimir "acessório" em vez de "acessório":

$$

$$\ begin {matrix} \ text {ak} & \ text {cec} & \ text {sou} & \ text {a} & \ text {p} \\ \ descendente & \ descendente & \ descendente & \ descendente & \ downarrow \\ \ text {a} & \ text {cc} & \ text {e} & \ text {soua} e \ text {p} \ end {matrix}$$

Como você provavelmente notou, este é um exemplo de uma partição não muito bem-sucedida: é claro que partes das palavras não se encaixavam tão bem quanto possível. Se as quantidades $$$P (\ text {ak} \ rightarrow \ text {a})$ e $$$P (\ text {p} \ rightarrow \ text {p})$ ainda não é tão ruim então $$$P (\ text {sou} \ rightarrow \ text {e})$ e $$$P (\ text {a} \ rightarrow \ text {soua})$ provavelmente eles tornarão a "pontuação" final dessa partição completamente triste. Uma partição mais bem-sucedida se parece com isso:

$$

$$\ begin {matrix} \ text {ak} & \ text {ce} & \ text {ss} & \ text {y} & \ text {ar} \\ \ descendente & \ descendente & \ descendente & \ descendente & \ downarrow \\ \ text {ak} & \ text {ce} & \ text {c} & \ text {y} & \ text {ar} \ end {matrix}$$

Aqui, tudo se encaixou imediatamente, e é claro que a probabilidade final será determinada principalmente pelo valor $$$P (\ text {ss} \ rightarrow \ text {s})$ .

Como calcular $$$P (s | w)$

Apesar do fato de existirem ordens de possíveis partições para duas palavras $$$O (2 ^ {| s | + | w |})$ usando o algoritmo de cálculo de programação dinâmica $$$P (s | w)$ pode ser feito muito rápido - por $$$O (| s | ^ 2 | w | ^ 2)$ . O próprio algoritmo será fortemente semelhante ao algoritmo de Wagner-Fisher para o cálculo da distância de Levenshtein .

Criaremos uma tabela retangular, cujas linhas corresponderão às letras da palavra correta e as colunas à selada. A célula na interseção da linha i e da coluna j até o final do algoritmo terá exatamente a probabilidade de obter s[:j] ao tentar imprimir w[:i] . Para calculá-lo, basta calcular os valores de todas as células nas linhas e colunas anteriores e passar por cima deles, multiplicando pelo valor correspondente $$$P (\ alpha \ rightarrow \ beta)$ . Por exemplo, se tivermos uma tabela preenchida


, em seguida, para preencher a célula na quarta linha e na terceira coluna (cinza), é necessário ter o máximo de $$$0,8 \ cdot P (\ text {cc} \ rightarrow \ text {c})$ e $$$0,16 \ cdot P (\ text {c} \ rightarrow \ text {k})$ . Ao mesmo tempo, percorremos todas as células destacadas na imagem em verde. Se considerarmos também modificações no formulário $$$P (\ alpha \ rightarrow \ text {linha vazia})$ e $$$P (\ text {linha vazia} \ rightarrow \ beta)$ , é necessário revisar as células destacadas em amarelo.

A complexidade desse algoritmo, como mencionei acima, é $$$O (| s | ^ 2 | w | ^ 2)$ : preenchemos a tabela $$$| s | \ times | w |$ e para preencher a célula (i, j), você precisa $$$O (i \ cdot j)$ operações. No entanto, se restringirmos nossa consideração a fragmentos não mais do que um comprimento limitado $$$L$ (por exemplo, não mais que duas letras, como em [4]), a complexidade diminuirá para $$$O (| s | \ cdot | w | \ cdot L ^ 2)$ . Para o idioma russo em minhas experiências, tomei $$$L = 3$ .

Como maximizar $$$P (s | w)$

Nós aprendemos a encontrar $$$P (s | w)$ para o tempo polinomial é bom. Mas precisamos aprender a encontrar rapidamente as melhores palavras em todo o dicionário. E os melhores não são $$$P (s | w)$ mas $$$P (w | s)$ ! De fato, é o suficiente para obtermos algumas melhores palavras razoáveis ​​(por exemplo, as 20 melhores) palavras para $$$P (s | w)$ , que enviaremos ao modelo de idioma para selecionar as correções mais apropriadas (mais sobre isso abaixo).

Para aprender a percorrer rapidamente o dicionário inteiro, observamos que a tabela apresentada acima terá muito em comum para duas palavras com prefixos comuns. De fato, se nós, corrigindo a palavra “acessório”, tentarmos preenchê-lo com as duas palavras do vocabulário “acessório” e “acessórios”, perceberemos que as nove primeiras linhas nelas não diferem! Se conseguirmos organizar uma passagem de dicionário para que as próximas duas palavras tenham prefixos comuns suficientemente longos, podemos salvar muitos cálculos.

E nós podemos. Vamos pegar as palavras do vocabulário e fazê-las tentar. Percorrendo-o em profundidade, obtemos a propriedade desejada: a maioria das etapas é do nó ao descendente, quando a tabela precisa preencher as últimas linhas.

Esse algoritmo, com algumas otimizações adicionais, permite classificar um dicionário de um idioma europeu típico em 50 a 100 mil palavras em cem milissegundos [2]. E o armazenamento em cache dos resultados tornará o processo ainda mais rápido.

Como obter $$$P (\ alpha \ rightarrow \ beta)$

Cálculo $$$P (\ alpha \ rightarrow \ beta)$ para todos os fragmentos em consideração - a parte mais interessante e não trivial da construção de um modelo de erro. É a partir dessas quantidades que sua qualidade dependerá.

A abordagem usada em [2, 4] é relativamente simples. Vamos encontrar muitos casais $$$(s_i, w_i)$ onde $$$w_i$ É a palavra correta do dicionário e $$$s_i$ - sua versão selada. (Como exatamente encontrá-los é um pouco menor.) Agora precisamos extrair desses pares as probabilidades de erros específicos (substituindo um fragmento por outro).

Para cada par, levamos seus componentes $$$w$ e $$$s$ e construa uma correspondência entre as letras, minimizando a distância de Levenshtein:

$$

$$\ begin {matrix} \ text {} & \ text {} & \ text {} & \ text {} & \ text {} & \ text {} & \ text {} & \ text {a} & \ text {p} \\ \ text {a} & \ text {k} & \ text {c} & \ text {e} & \ text {c} e \ text {} & \ text {y } & \ text {a} & \ text {p} \ end {matrix}$$

Agora vemos imediatamente as substituições: a → a, e → e, c → c, c → uma string vazia e assim por diante. Também vemos substituições de dois ou mais caracteres: ak → ak, ce → si, ec → is, ss → s, ses → sis, ess → is e outro e outro. Todas essas substituições devem ser contadas, e cada uma das vezes que a palavra s ocorrer no corpus (se pegarmos as palavras do corpus, o que é muito provável).

Depois de passar em todos os pares $$$(s_i, w_i)$ por probabilidade $$$P (\ alpha \ rightarrow \ beta)$ o número de substituições α → β que ocorreram em nossos pares é aceito (levando em consideração a ocorrência das palavras correspondentes) dividido pelo número de repetições do fragmento α.

Como encontrar casais $$$(s_i, w_i)$ ? Em [4], essa abordagem foi proposta. Veja o corpo grande de conteúdo gerado pelo usuário (UGC). No caso do Google, eram apenas os textos de centenas de milhões de páginas da web; A nossa possui milhões de pesquisas e críticas de usuários. Supõe-se que geralmente a palavra correta seja encontrada no corpus com mais frequência do que qualquer uma das variantes erradas. Então, vamos encontrar palavras para cada palavra próximas a ele de Levenshtein do corpus, que são muito menos populares (por exemplo, dez vezes). Tome popular $$$w$ , menos popular - para $$$s$ . Então, temos um conjunto barulhento, mas bastante grande, de pares para treinar.

Esse algoritmo de correspondência de pares deixa muito espaço para melhorias. Em [4], apenas um filtro por ocorrência ( $$$w$ dez vezes mais popular que $$$s$ ), mas os autores deste artigo estão tentando fazer uma fofoca, sem usar nenhum conhecimento a priori do idioma. Se considerarmos apenas o idioma russo, podemos, por exemplo, usar um conjunto de dicionários de formas de palavras em russo e deixar apenas pares com a palavra $$$w$ encontrado no dicionário (não é uma boa ideia, porque o dicionário provavelmente não terá vocabulário específico para o serviço) ou, por outro lado, descartar pares com a palavra s encontrada no dicionário (ou seja, é quase garantido que não será lacrado).

Para melhorar a qualidade dos pares recebidos, escrevi uma função simples que determina se os usuários usam duas palavras como sinônimos. A lógica é simples: se as palavras w e s são frequentemente encontradas cercadas pelas mesmas palavras, provavelmente são sinônimos - o que, à luz da proximidade de Levenshtein, significa que uma palavra menos popular é provavelmente uma versão errônea de uma mais popular. Para esses cálculos, usei as estatísticas da ocorrência de trigramas (frases de três palavras) construídas para o modelo de linguagem abaixo.

Modelo de linguagem

Então, agora, para uma determinada palavra do dicionário w, precisamos calcular $$$P (w)$ - a probabilidade de seu uso pelo usuário. A solução mais simples é considerar a ocorrência de uma palavra em algum tipo de caso grande. Em geral, provavelmente, qualquer modelo de linguagem começa com a coleta de um grande corpus de textos e contando a ocorrência de palavras nele. Mas não devemos nos limitar a isso: de fato, ao calcular P (w), também podemos levar em conta a frase na qual estamos tentando corrigir a palavra e qualquer outro contexto externo. A tarefa se transforma em uma tarefa de cálculo $$$P (w_1w_2 \ ldots w_k)$ onde um $$$w_i$ - a palavra em que corrigimos o erro de digitação e pela qual estamos contando agora $$$P (w)$ e o resto $$$w_i$ - As palavras que cercam a palavra corrigida na solicitação do usuário.

Para aprender a considerá-los, vale a pena revisar o corpus novamente e compilar estatísticas de n-gramas, sequências de palavras. Geralmente, sequências de comprimento limitado; Limitei-me aos trigramas para não aumentar o índice, mas tudo depende da sua força de espírito (e do tamanho do caso - em um caso pequeno, até as estatísticas dos trigramas serão muito barulhentas).

O modelo tradicional da linguagem n-grama se parece com isso. Para a frase $$$w_1w_2 \ ldots w_k$ sua probabilidade é calculada pela fórmula

$$

$$P (w_1w_2 \ ldots w_k) = P (w_1) \ cdot P (w_2 | w_1) \ cdot P (w_3 | w_1w_2) P (w_k | w_1w_2w_ {k-1}) \ ,,$$

onde $$$P (w_1)$ - diretamente a frequência da palavra, e $$$P (w_3 | w_1w_2)$ - probabilidade de palavras $$$w_3$ desde que antes dele ir $$$w_1w_2$ - nada além da razão da frequência do trigrama $$$w_1 w_2 w_3$ para frequência de bigram $$$w_1 w_2$ . (Observe que esta fórmula é simplesmente o resultado do uso repetido da fórmula de Bayes.)

Em outras palavras, se queremos calcular $$$P (\ text {moldura de sabão para mãe})$ , denotando a frequência de um n-grama arbitrário em $$$f$ nós obtemos a fórmula

$$

$$P (\ text {quadro de sabão da mãe}) = f (\ text {mãe}) \ cdot \ frac {f (\ text {sabão da mãe})} {f (\ text {mãe})} \ cdot \ frac { f (\ text {sabonete mãe})} {f (\ text {sabonete mãe})} = f (\ text {sabonete mãe}) \,.$$

Isso é lógico? É lógico. No entanto, as dificuldades começam quando as frases se tornam mais longas. E se um usuário digitasse uma consulta de pesquisa de dez palavras com detalhes impressionantes? Não queremos manter estatísticas para todos os 10 gramas - isso é caro, e os dados provavelmente serão barulhentos e não indicativos. Queremos conviver com n-gramas de comprimento limitado - por exemplo, o comprimento 3 já proposto acima.

É aqui que a fórmula acima é útil. Vamos supor que a probabilidade de uma palavra aparecer no final de uma frase seja significativamente afetada apenas por algumas palavras imediatamente à sua frente, ou seja,

$$

$$P (w_k | w_1w_2 \ ldots w_ {k-1}) \ aprox P (w_k | w_ {k-L + 1} \ ldots w_ {k-1}) \,.$$

Colocando $$$L = 3$ , para uma frase mais longa, obtemos a fórmula


$$$P (\ text {carl roubou corais de Clara}) \ approx f (\ text {carl}) \ cdot \ frac {f (\ text {carl})} {f (\ text {carl})} \ cdot \ frac {f (\ text {carl de clara})} {f (\ text {carl de})} \ cdot \ frac {f (\ text {roubou de clara})} {f (\ text {de clara} )} \ cdot \ frac {f (\ texto {claire roubou coral})} {f (\ texto {claire roubou})} \,.$


Observe: a frase consiste em cinco palavras, mas n-gramas não mais que três aparecem na fórmula. Isso é exatamente o que buscávamos.

Restou um momento magro. E se o usuário digitasse uma frase muito estranha e os n-gramas correspondentes em nossas estatísticas, e de maneira nenhuma? Seria fácil para n-gramas desconhecidos colocar $$$f = 0$ se não fosse necessário dividir por esse valor. Aqui vem a ajuda da suavização (suavização), que pode ser feita de diferentes maneiras; no entanto, uma discussão detalhada de abordagens anti-aliasing sérias, como a suavização de Kneser-Ney, está muito além do escopo deste artigo.

Como corrigir frases

Discutimos o último ponto sutil antes de avançarmos para a implementação. A declaração do problema que descrevi acima implicava que há uma palavra e ela precisa ser corrigida. Em seguida, esclarecemos que essa palavra pode estar no meio de uma frase, entre outras palavras, e elas também precisam ser levadas em consideração, escolhendo a melhor correção. Mas, na realidade, os usuários simplesmente nos enviam frases sem especificar qual palavra está escrita; geralmente algumas palavras ou mesmo todas precisam ser corrigidas.

Pode haver muitas abordagens. Por exemplo, você pode levar em consideração apenas o contexto esquerdo da palavra na frase. Então, seguindo as palavras da esquerda para a direita e corrigindo-as conforme necessário, obteremos uma nova frase de alguma qualidade. A qualidade será ruim se, por exemplo, a primeira palavra for como várias palavras populares e escolhermos a opção errada. A frase restante inteira (possivelmente inicialmente completamente livre de erros) será ajustada por nós para a primeira palavra errada e podemos obter um texto completamente irrelevante para o original.

Você pode considerar as palavras individualmente e aplicar um determinado classificador para entender se a palavra especificada está selada ou não, conforme sugerido em [4]. O classificador é treinado nas probabilidades que já sabemos contar e em vários outros recursos. Se o classificador diz o que precisa ser corrigido, estamos corrigindo, considerando o contexto existente. Novamente, se várias palavras estiverem escritas incorretamente, você terá que tomar uma decisão sobre a primeira delas com base no contexto com os erros, o que pode levar a problemas de qualidade.

Na implementação de nosso tutor, usamos essa abordagem. Vamos por cada palavra $$$s_i$ em nossa frase, usando o modelo de erro, encontramos as palavras do dicionário N mais importantes que podem ser entendidas, as concatenamos em frases de todas as maneiras possíveis e para cada uma $$$N ^ K$ frases resultantes em que $$$K$ - o número de palavras na frase original, calcule honestamente o valor

$$

$$P (s_1 | w_1) \ cdot P (s_K | w_K) \ cdot P (s_K | w_K) \ cdot P (w_1w_2 \ ldots w_K) ^ {\ lambda} \,.$$

Aqui $$$s_i$ - palavras inseridas pelo usuário, $$$w_i$ - correções selecionadas para eles (pelas quais estamos analisando agora), e $$$\ lambda$ - coeficiente determinado pela qualidade comparativa do modelo de erro e modelo de linguagem (coeficiente grande - confiamos mais no modelo de linguagem, coeficiente pequeno - confiamos mais no modelo de erro), proposto em [4]. No total, para cada frase, multiplicamos as probabilidades de palavras individuais a serem corrigidas nas variantes de dicionário correspondentes, e também multiplicamos isso pela probabilidade de toda a frase em nosso idioma. O resultado do algoritmo é uma frase das palavras do dicionário que maximiza esse valor.

Então pare o que? Força bruta $$$N ^ K$ frases?

Felizmente, devido ao fato de termos limitado o comprimento de n-gramas, é possível encontrar um máximo em todas as frases muito mais rapidamente. Lembre-se: acima, simplificamos a fórmula para $$$P (w_1w_2 \ ldots w_K)$ de modo que passou a depender apenas de frequências de n gramas de comprimento não superior a três:

$$

$$P (w_1w_2 \ ldots w_K) = P (w_1) \ cdot P (w_2 | w_1) \ cdot P (w_3 | w_1w_2) \ cdot \ ldots \ cdot P (w_K | w_ {K-2} w_ {K-1 }) \,.$$

Se multiplicarmos esse valor por $$$P (s_i | w_i)$ e tente maximizar $$$w_K$ , veremos que é suficiente resolver todos os tipos de $$$w_ {K-2}$ e $$$w_ {K-1}$ e resolver o problema para eles - ou seja, para frases $$$w_1w_2 \ ldots w_ {K-2} w_ {K-1}$ . No total, o problema é resolvido pela programação dinâmica em $$$O (KN ^ 3)$ .

Implementação

Montando o estojo e contando os n-gramas

Farei uma reserva imediatamente: não havia muitos dados à minha disposição para iniciar um MapReduce complexo. Então, eu apenas coletei todos os textos de resenhas, comentários e consultas de pesquisa em russo (as descrições de mercadorias, infelizmente, vêm em inglês, e o uso dos resultados da tradução automática piorou do que melhorou os resultados) do nosso serviço em um arquivo de texto e configurou o servidor para a contagem da noite trigramas com um script Python simples.

Como dicionário, peguei as principais palavras com frequência para obter cerca de cem mil palavras. Foram excluídas palavras muito longas (mais de 20 caracteres) e muito curtas (menos de três caracteres, exceto palavras conhecidas e conhecidas em russo). r"^[a-z0-9]{2}$" separadamente as palavras sobre a regularidade r"^[a-z0-9]{2}$" - para que as versões dos iPhones e outros identificadores interessantes de comprimento 2 sobrevivessem.

Ao contar bigramas e trigramas em uma frase, pode ocorrer uma palavra que não seja do dicionário. Nesse caso, joguei fora essa palavra e bati a frase inteira em duas partes (antes e depois dessa palavra), com as quais trabalhei separadamente. Então, para a frase " Você sabe o que é" abyrvalg "? Isso é ... O chefe, colega "levará em conta os trigramas" Você sabe "," você sabe o que "," sabe o que é "e" este é o principal colega de pescador "(a menos que, é claro, a palavra" chefe "caia no dicionário ...).

Nós treinamos o modelo de erro

Além disso, realizei todo o processamento de dados no Jupyter. As estatísticas de n-gramas são carregadas do JSON, o pós-processamento é realizado para encontrar rapidamente palavras próximas umas das outras, de acordo com Levenshtein, e para pares no loop, é chamada uma função (bastante complicada) que organiza as palavras e extrai edições curtas da forma ss → c (no spoiler).


O cálculo das edições em si parece elementar, embora possa demorar muito tempo.

Aplicar modelo de erro

Esta parte é implementada como um micro serviço on Go, conectado ao back-end principal via gRPC. O algoritmo descrito pelos próprios Brill e Moore [2], com pequenas otimizações, foi implementado. Como resultado, funciona para mim duas vezes mais devagar do que os autores afirmavam; Não pretendo julgar se está em Go ou em mim. Mas, no decorrer da criação de perfil, aprendi um pouco de novo sobre o Go.

• Não use math.Max para contar o máximo. Isso é cerca de três vezes mais lento do que if a > b { b = a } ! Basta olhar para a implementação desta função :
  

   // Max returns the larger of x or y. // // Special cases are: // Max(x, +Inf) = Max(+Inf, x) = +Inf // Max(x, NaN) = Max(NaN, x) = NaN // Max(+0, ±0) = Max(±0, +0) = +0 // Max(-0, -0) = -0 func Max(x, y float64) float64 func max(x, y float64) float64 { // special cases switch { case IsInf(x, 1) || IsInf(y, 1): return Inf(1) case IsNaN(x) || IsNaN(y): return NaN() case x == 0 && x == y: if Signbit(x) { return y } return x } if x > y { return x } return y } 

  
  A menos que você precise +0 para ser necessariamente maior que -0, não use math.Max .
  
• Não use uma tabela de hash se você puder usar uma matriz. Obviamente, este é um conselho bastante óbvio. Eu tive que renumerar caracteres Unicode em números no início do programa para usá-los como índices na matriz descendente do nó trie (essa pesquisa foi uma operação muito comum).
  
• As chamadas de retorno no Go não são baratas. Durante a refatoração durante a revisão de código, algumas das minhas tentativas de dissociação diminuíram significativamente o programa, apesar do fato de o algoritmo não ter sido formalmente alterado. Desde então, sou de opinião que o compilador de otimização Go tem espaço para crescer.
  

Aplicar um modelo de idioma

Aqui, sem surpresas, o algoritmo de programação dinâmica descrito na seção acima foi implementado. Esse componente teve menos trabalho - a parte mais lenta é a aplicação do modelo de erro. Portanto, entre essas duas camadas, o armazenamento em cache do modelo de erro resulta em Redis adicionalmente.

Resultados

Com base nos resultados deste trabalho (que levou cerca de um mês), realizamos um protetor de teste A / B em nossos usuários. Em vez de 10% dos resultados de pesquisa vazios entre todas as consultas de pesquisa que tínhamos antes da introdução do tutor, havia 5% delas; basicamente, os pedidos restantes são para mercadorias que simplesmente não temos na plataforma. O número de sessões sem uma segunda consulta de pesquisa também aumentou (e várias outras métricas desse tipo relacionadas ao UX). As métricas relacionadas ao dinheiro, no entanto, não mudaram significativamente - isso foi inesperado e nos levou a uma análise completa e a uma verificação cruzada de outras métricas.

Conclusão

Stephen Hawking já foi informado de que todas as fórmulas incluídas no livro reduziriam pela metade o número de leitores. Bem, neste artigo, existem cerca de cinquenta deles - parabenizo você, um dos cerca de$$$10^{-10}$ Leitores que alcançam este lugar!

Bônus

Referências

[1] MD Kernighan, Igreja KW, WA Gale. Um programa de correção ortográfica baseado em um modelo de canal ruidoso . Anais da 13ª conferência sobre linguística computacional - Volume 2, 1990.

[2] E.Brill, RC Moore. Um modelo de erro aprimorado para correção ortográfica de canal ruidoso . Anais da 38ª Reunião Anual sobre Associação para Linguística Computacional, 2000.

[3] T. Brants, AC Popat, P. Xu, FJ Och, J. Dean. Modelos de linguagem grande em tradução automática . Anais da Conferência de 2007 sobre Métodos Empíricos no Processamento de Linguagem Natural.

[4] C. Whitelaw, B. Hutchinson, GY Chung, G. Ellis. Usando a Web para verificação ortográfica e correção automática independentes do idioma. Anais da Conferência de 2009 sobre Métodos Empíricos no Processamento de Linguagem Natural: Volume 2.