Redes de densidade de mistura

Olá pessoal!

Vamos falar sobre, como você deve ter adivinhado, redes neurais e aprendizado de máquina. Pelo nome, fica claro o que será dito sobre as redes de densidade de mistura, e então apenas a MDN, não quero traduzir o nome e deixá-lo como está. Sim, sim, sim ... haverá um pouco de matemática chata e teoria das probabilidades, mas sem ela, infelizmente ou felizmente, cabe a você decidir o quão difícil é imaginar o mundo do aprendizado de máquina. Mas me apresso em tranquilizá-lo, será relativamente pequeno e não será muito difícil. De qualquer forma, você pode pular, mas basta olhar para uma pequena quantidade de código no Python e no PyTorch, isso mesmo, escreveremos a rede usando o PyTorch, além de vários gráficos com os resultados. Mas o mais importante é que haverá uma oportunidade de entender um pouco e entender o que são redes MD.

Bem, vamos começar!

---

Regressão

Para começar, vamos atualizar um pouco nosso conhecimento e relembrar brevemente, o que é regressão linear .

Nós temos um vetor $$$X = \ {x_1, x_2, ..., x_n \}$ precisamos prever o valor $$$Y$ , que de alguma forma depende $$$X$ usando algum modelo linear:

$$

$$\ hat {Y} = X ^ T \ hat {\ beta}$$

Como função de erro, usaremos o erro ao quadrado:

$$

$$SE (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 = \ sum_ {i = 1} ^ N (y_i-x_i ^ T \ hat {\ beta} ) ^ 2$$

Esse problema pode ser resolvido diretamente pegando a derivada de SE e definindo seu valor como zero:

$$

$$\ frac {\ delta SE (\ beta)} {\ delta \ beta} = 2X ^ T (\ mathbf {y} -X \ beta) = 0$$

Assim, simplesmente encontramos seu mínimo, e SE é uma função quadrática, o que significa que o mínimo sempre existirá. Depois disso, você já pode encontrar facilmente $$$\ beta$ :

$$

$$\ hat \ beta = (X ^ TX) ^ {- 1} X ^ T \ mathbf {y}$$

Isso é tudo, o problema está resolvido. É aqui que terminamos de lembrar o que é regressão linear.

Obviamente, a dependência inerente à natureza da geração de dados pode ser diferente e, então, alguma não linearidade já deve ser adicionada ao nosso modelo. Resolver o problema de regressão diretamente para dados grandes e reais também é uma má ideia, pois existe uma matriz $$$X ^ TX$ dimensões $$$n \ vezes n$ , e ainda é necessário encontrar sua matriz inversa, e muitas vezes acontece que essa matriz simplesmente não existe. Nesse caso, vários métodos baseados na descida do gradiente vêm em nosso auxílio. A não linearidade dos modelos pode ser implementada de várias maneiras, incluindo o uso de redes neurais.

Mas agora, não vamos falar sobre isso, mas sobre funções de erro. Qual é a diferença entre SE e Probabilidade de log quando os dados podem ter um relacionamento não linear?


Pare com isso! Probabilidade? Isso é algo da teoria das probabilidades. Isso mesmo - é pura teoria das probabilidades. Mas como o desvio quadrático pode estar relacionado à função de probabilidade? E como acontece. Está relacionado à busca da máxima verossimilhança (máxima verossimilhança) e da distribuição normal, para ser mais preciso, com sua média $$$\ mu$ .

Para perceber que é assim, vejamos novamente a função de desvio quadrado:

$$

$$RSS (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 \ qquad \ qquad (1)$$

Agora, suponha que a função de probabilidade tenha uma forma normal, ou seja, uma distribuição gaussiana ou normal:

$$

$$L (X) = p (X | \ theta) = \ prod ^ X \ mathcal {N} (x_i; \ mu, \ sigma ^ 2)$$

Em geral, qual é a função de probabilidade e qual é o significado dela, não vou contar; você pode ler sobre isso em outro lugar; também deve se familiarizar com o conceito de probabilidade condicional, o teorema de Bayes e muito mais, para uma compreensão mais profunda. Tudo isso entra na pura teoria da probabilidade, estudada tanto na escola quanto na universidade.

Agora, lembrando a fórmula de distribuição normal, obtemos:

$$

$$L (X; \ mu, \ sigma ^ 2) = \ prod ^ X \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {(x_i- \ mu) ^ 2} {2 \ sigma ^ 2}} \ qquad \ qquad (2)$$

E se colocarmos o desvio padrão $$$\ sigma ^ 2 = 1$ e remova todas as constantes da fórmula (2), apenas remova, não reduza, porque encontrar o mínimo da função não depende delas. Então vamos ver isso:

$$

$$L (X; \ mu, \ sigma ^ 2) \ sim \ prod ^ Xe ^ {- (x_i- \ mu) ^ 2}$$

Ainda nada como? Não? Bem, e se pegarmos o logaritmo da função? No logaritmo, existem algumas vantagens: a multiplicação se transformará em uma soma, um grau em multiplicação e $$$\ log {e} = 1$ - para esta propriedade, vale esclarecer que estamos falando do logaritmo natural e, estritamente falando $$$\ ln {e} = 1$ . E, em geral, o logaritmo de uma função não altera seu máximo, e esse é o recurso mais importante para nós. A conexão com o Log-Likelihood e Likelihood e por que isso será útil será descrita abaixo em uma pequena digressão. E o que fizemos: removemos todas as constantes e assumimos o logaritmo da função de probabilidade. Eles também removeram o sinal de menos, transformando a Probabilidade de log em Probabilidade de log negativo (NLL); a conexão entre eles também será descrita como um bônus. Como resultado, obtivemos a função NLL:

$$

$$\ log L (X; \ mu, I ^ 2) \ sim \ sum (X- \ mu) ^ 2$$

Veja novamente a função RSS (1). Sim, eles são iguais! Exatamente! Também é visto que $$$\ mu = \ hat {y}$ .

Se você usa a função de desvio padrão do MSE, obtemos disso:

$$

$$\ nome do operador {argmin} MSE (\ beta) \ sim \ nome do operador {argmax} \ mathbb {E} _ {X \ sim P_ {dados}} \ log P_ {modelo} (x; \ beta)$$

onde $$$\ mathbb {E}$ - expectativa matemática $$$\ beta$ - parâmetros do modelo, no futuro, iremos denotá-los como: $$$\ theta$ .

Conclusão: Se usarmos a família LS como função de erro na questão da regressão, resolveremos essencialmente o problema de encontrar a função de máxima verossimilhança no caso em que a distribuição é gaussiana. E o valor previsto $$$\ hat {y}$ igual à média na distribuição normal. E agora sabemos como tudo isso está conectado, como a teoria das probabilidades está relacionada (com sua função de probabilidade e distribuição normal) e métodos de desvio padrão ou OLS. Mais detalhes sobre isso podem ser encontrados em [2].

E aqui está o bônus prometido. Como estamos falando das relações entre as várias funções de erro, consideraremos (não necessariamente para ser lido):

Regressão de rede neural

Então chegamos a uma prática mais interessante. Vamos ver como você pode resolver o problema de regressão usando redes neurais (redes neurais). Implementaremos tudo na linguagem de programação Python. Para criar uma rede, usamos a biblioteca de aprendizado profundo do PyTorch.

Geração de dados de origem

Dados de entrada $$$\ mathbf {X} \ in \ mathbb {R} ^ N$ gerar usando uma distribuição uniforme, leve o intervalo de -15 a 15, $$$\ mathbf {X} \ em U [-15, 15]$ . Pontos $$$\ mathbf {Y}$ obtemos usando a equação:

$$

$$\ mathbf {Y} = 0,5 \ mathbf {X} + 8 \ sin (0,3 \ mathbf {X}) + ruído \ qquad \ qquad (3)$$

onde $$$noise$ É um vetor de ruído de dimensão $$$N$ obtido usando a distribuição normal com parâmetros: $$$\ mu = 0, \ sigma ^ 2 = 1$ .



O gráfico dos dados recebidos.

Construção de rede

Crie uma rede neural de avanço de alimentação regular ou FFNN.


Nossa rede consiste em uma camada oculta com uma dimensão de 40 neurônios e com uma função de ativação - tangente hiperbólica:

$$

$$\ tanh x = \ frac {e ^ x-e ^ {- x}} {e ^ x + e ^ {- x}} \ qquad \ qquad (4)$$

A camada de saída é uma transformação linear normal sem uma função de ativação.

Aprendendo e obtendo resultados

Como otimizador, usaremos o AdamOptimizer. O número de épocas de estudo = 2000, a taxa de aprendizagem (taxa de aprendizagem ou lr) = 0,1.


Agora vamos ver os resultados da aprendizagem.


Gráfico dos valores da função MSE, dependendo da iteração do treinamento; gráfico de valores para dados de treinamento e dados de teste.


Resultados reais e previstos em dados de teste.

Dados invertidos

Nós complicamos a tarefa e invertemos os dados.



Gráfico de dados invertidos.

Para previsão $$$\ mathbf {\ hat Y}$ vamos usar a rede de distribuição direta da seção anterior e ver como ela lida com isso.

 inv_train_losses, inv_test_losses = train(net, x_train_inv, y_train_inv, x_test_inv, y_test_inv) 

Gráfico dos valores da função MSE, dependendo da iteração do treinamento; gráfico dos valores dos dados de treinamento e de teste.


Resultados reais e previstos em dados de teste.

Como você pode ver nos gráficos acima, nossa rede não lidou com esses dados, simplesmente não é capaz de prever. E tudo isso aconteceu porque em um problema tão invertido por um ponto $$$x$ pode corresponder a vários pontos $$$y$ . Você pergunta, e o barulho? Ele também criou uma situação em que, por um $$$x$ poderia obter alguns valores $$$y$ . Sim está certo. Mas o ponto principal é que, apesar do barulho, era tudo uma distribuição definida. E como nosso modelo previu essencialmente $$$p (y | x)$ , e no caso de MSE, era o valor médio para a distribuição normal (por que é descrito na primeira parte do artigo), depois lidou bem com a tarefa "direta". Caso contrário, obteremos várias distribuições diferentes para um $$$x$ e, portanto, não podemos obter um bom resultado com apenas uma distribuição normal.

Rede de densidade de mistura

A diversão começa! O que é rede de densidade de mistura (a seguir denominada rede MDN ou MD)? Em geral, este é um determinado modelo capaz de simular várias distribuições ao mesmo tempo:

$$

$$p (\ mathbf {y} | \ mathbf {x}; \ theta) = \ sum_k ^ K \ pi_k (\ mathbf {x}) \ mathcal {N} (\ mathbf {y}; \ mu_k (\ mathbf { x}), \ sigma ^ 2 (\ mathbf {x})) \ qquad \ qquad (5)$$

Que fórmula estranha, você diz. Vamos descobrir. Nossa rede MD está aprendendo a modelar a média $$$\ mu$ e variação $$$\ sigma ^ 2$ para várias distribuições. Na fórmula (5) $$$\ pi_k (\ mathbf {x})$ - os chamados fatores de significância de uma distribuição separada para cada ponto $$$x_i \ in \ mathbf {x}$ , um determinado fator de mistura ou quanto cada uma das distribuições contribui para um determinado ponto. Total lá $$$K$ distribuições.

Mais algumas palavras sobre $$$\ pi_k (\ mathbf {x})$ - de fato, isso também é uma distribuição e representa a probabilidade de que, por um ponto $$$x_i \ in \ mathbf {x}$ será uma condição $$$k$ .

Ah, novamente, essa matemática, já vamos escrever algo. E assim, começaremos a realizar uma rede. Para a nossa rede, tomamos $$$K = 30$ .

 self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance 

Defina as camadas de saída para nossa rede:

 x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x) 

Escrevemos a função de erro ou função de perda, fórmula (5):

 def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses)) 

Nossa rede MD está pronta para funcionar. Quase pronto. Resta treiná-la e analisar os resultados.



O gráfico dos valores da função de perda dependendo da iteração do treinamento; o gráfico de valores para dados de treinamento e dados de teste.

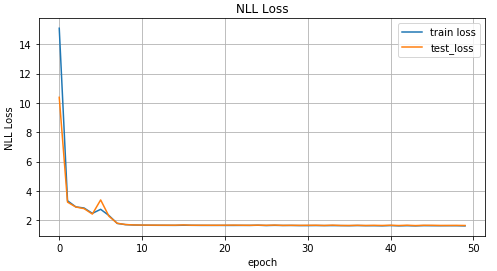
Como nossa rede aprendeu os valores médios para várias distribuições, vejamos o seguinte:

 pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv))) 

Gráfico para os dois valores médios mais prováveis ​​para cada ponto (esquerda). Gráfico para os 4 valores médios mais prováveis ​​para cada ponto (à direita).


Gráfico para todos os valores médios para cada ponto.

Para prever dados, selecionaremos aleatoriamente vários valores $$$\ mu$ e $$$\ sigma ^ 2$ com base no valor $$$\ pi_k (\ mathbf {x})$ . E então, com base neles, para gerar dados de destino $$$\ hat {y}$ usando distribuição normal.



Dados previstos para 10 valores selecionados aleatoriamente $$$\ mu$ e $$$\ sigma ^ 2$ (esquerda) e para dois (direita).

Pode-se ver pelas figuras que a MDN fez um excelente trabalho com a tarefa "inversa".

Usando dados mais complexos

Vamos ver como nossa rede MD lida com dados mais complexos, como dados em espiral. A equação da espiral hiperbólica nas coordenadas cartesianas:

$$

$$x = \ rho \ cos \ phi \\\ qquad \ qquad \ qquad \ qquad \ qquad \ qquad (6) \\ y = \ rho \ sin \ phi \\ $$

Gráfico de dados em espiral.

Por diversão, vamos ver como uma rede Feed-Forward regular lidará com essa tarefa.


Como esperado, a rede Feed-Forward não pode resolver o problema de regressão para esses dados.

Utilizamos a rede MD descrita e criada anteriormente para treinamento em dados em espiral.


A Rede de densidade da mistura fez um ótimo trabalho nessa situação.

Conclusão

No início deste artigo, lembramos os princípios básicos da regressão linear. Vimos isso em comum entre encontrar a média para a distribuição normal e MSE. Desmontado como conectado NLL e entropia cruzada. E o mais importante, descobrimos o modelo MDN, que é capaz de aprender com os dados obtidos de uma distribuição mista. Espero que o artigo seja compreensível e interessante, apesar de haver um pouco de matemática.

O código completo pode ser visualizado no GitHub .

---

Literatura

1. Redes de densidade de mistura (Christopher M. Bishop, Grupo de Pesquisa em Computação Neural, Departamento de Ciência da Computação e Matemática Aplicada, Universidade de Aston, Birmingham) - o artigo descreve completamente a teoria das redes de MD.
2. Mínimos quadrados e máxima verossimilhança (MROsborne)