Há já algum tempo que uso o QML para criar interfaces gráficas, mas até agora não houve oportunidade de trabalhar em um projeto real com a
API de localização Qt e o mapa QML.
Portanto, tornou-se interessante experimentar esse componente para a construção de vias aéreas.
Sob o cortador, está a descrição da implementação do editor, para criar caminhos semelhantes no mapa:

Para simplificar a implementação, nossos aviões voam no plano 2D na mesma altura. A velocidade e a sobrecarga permitida são fixas - 920 km / he 3g, o que fornece um raio de viragem
A trajetória consiste nos seguintes segmentos:

onde S é o início da manobra (é o ponto de saída da anterior), M é o início da curva, E é a saída e F é o ponto final (M para a próxima).
Para calcular o ponto de entrada e saída da trajetória, usei a
equação de uma tangente a um círculo, os cálculos acabaram sendo bastante pesados, tenho certeza de que isso pode ser simplificado.
void Manoeuvre::calculate() {
Depois de concluir o erro de cálculo do modelo matemático de nossa trajetória, passamos a trabalhar diretamente com o mapa. Uma opção natural para a construção de polilinhas em um mapa QML é adicionar o
MapPolyline diretamente ao mapa.
Map { id: map plugin: Plugin { name: "osm" } MapPolyline { path: [ { latitude: -27, longitude: 153.0 }, ... ] } }
Inicialmente, eu queria oferecer ao usuário a oportunidade de simular cada seção subseqüente da rota "on the fly" - para criar um efeito do movimento da trajetória atrás do cursor.
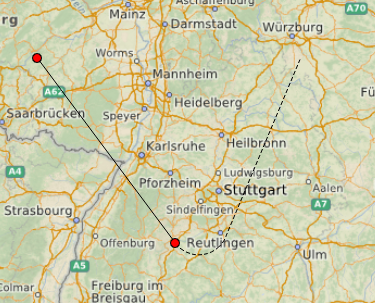
Alterar o
caminho ao mover o cursor é uma operação bastante cara, então tentei usar caminhos preliminares de “pixel” que são exibidos até o usuário finalmente salvar a rota.
Repeater { id: trajectoryView model: flightRegistry.hasActiveFlight ? flightRegistry.flightModel : [] FlightItem { anchors.fill: parent startPoint: start endPoint: end manoeuvreRect: rect manoeuvreStartAngle: startAngle manoeuvreSpanAngle: spanAngle isVirtualLink: isVirtual } }
FlightItem é um
QQuickItem e
QAbstractListModel flightModel permite atualizar as seções necessárias da trajetória ao alterar dados para manobra.
QVariant FlightModel::data(const QModelIndex &index, int role) const { if (!index.isValid()) { return QVariant(); } switch (role) { case FlightRoles::StartPoint: return mFlight->flightSegment(index.row()).line().p1(); case FlightRoles::EndPoint: return mFlight->flightSegment(index.row()).line().p2(); ... }
Essa atualização ao vivo permite que você avise o usuário sobre manobras irrealizáveis.
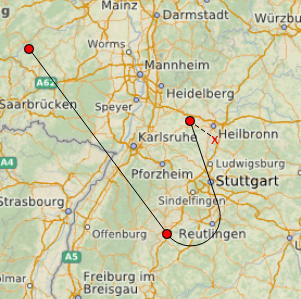
Somente após a conclusão da criação da via aérea (por exemplo, com o clique direito do mouse) a rota será finalmente adicionada ao Mapa QML como um GeoPath com possibilidade de georreferenciamento (até o momento em que o mapa não possa ser movido e ampliado, os pixels não sabem nada sobre longitude e latitude).
Para recalcular um segmento de pixel em uma coordenada geográfica, para iniciantes, precisamos usar para cada manobra um sistema de coordenadas local ao ponto de entrada da manobra (nosso ponto S).
QPointF FlightGeoRoute::toPlaneCoordinate(const QGeoCoordinate &origin, const QGeoCoordinate &point) { auto distance = origin.distanceTo(point); auto azimuth = origin.azimuthTo(point); auto x = qSin(qDegreesToRadians(azimuth)) * distance; auto y = qCos(qDegreesToRadians(azimuth)) * distance; return QPointF(x, y); }
Após recalcularmos a manobra já em metros, é necessário fazer a operação reversa e conhecer o georreferenciamento do ponto S para transferir os medidores para latitude-longitude.
QGeoCoordinate FlightGeoRoute::toGeoCoordinate(const QGeoCoordinate &origin, const QPointF &point) { auto distance = qSqrt(point.x()*point.x() + point.y()*point.y()); auto radianAngle = qAtan2(point.x(), point.y()); auto azimuth = qRadiansToDegrees(radianAngle < 0 ? radianAngle + 2*M_PI : radianAngle); return origin.atDistanceAndAzimuth(distance, azimuth); }
Do ponto de vista formal, é impossível, é claro, considerar nossa trajetória “pixel” e “em metros” idêntica, mas me pareceu muito saboroso olhar para o futuro e mostrar ao usuário o que acontecerá (ou não acontecerá se o avião não voar assim) quando ele clicará na próxima vez. Depois de finalizar a trajetória (difere um pouco do pixel em cores e transparência, pois mesmo linhas quebradas estáticas não parecem muito suaves no mapa).
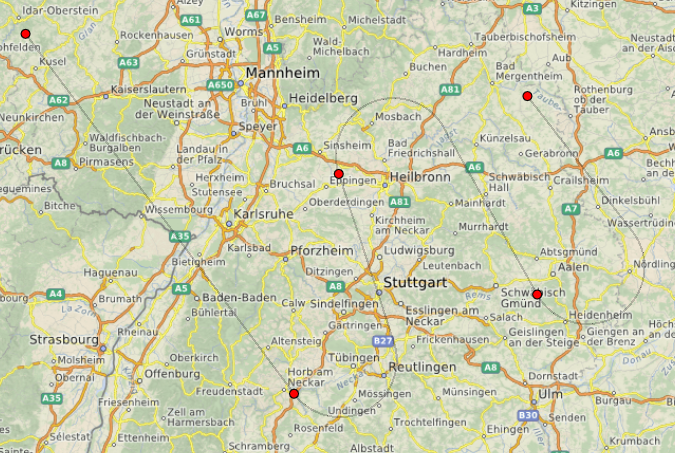
As fontes estão disponíveis
aqui ; para compilação, usei o Qt 5.11.2.
Na próxima parte, ensinaremos nosso editor a mover os pontos de referência da trajetória, além de salvar / abrir as trilhas existentes para simulação subsequente do movimento da aeronave.