Este é o segundo artigo sobre a análise e estudo de materiais da competição para a busca de navios no mar. Mas agora vamos estudar as propriedades das sequências de treinamento. Vamos tentar encontrar informações em excesso, redundância nos dados de origem e excluí-los.

Este artigo também é simplesmente o resultado de curiosidade e interesse ocioso, nada disso é encontrado na prática e, para tarefas práticas, não há quase nada para copiar e colar. Este é um pequeno estudo das propriedades da sequência de treinamento - o raciocínio e o código do autor são apresentados, você pode verificar / complementar / alterar tudo sozinho.
A competição de busca marinha kaggle terminou recentemente. A Airbus propôs analisar imagens de satélite do mar com e sem navios. Um total de 192555 imagens 768x768x3 - é 340 720 680 960 bytes se uint8 e essa é uma quantidade enorme de informações e houve uma suspeita vaga de que nem todas as imagens são necessárias para o treinamento da rede e nessa quantidade de repetição e redundância são óbvias. Ao treinar uma rede, é habitual separar alguns dados e não usá-los no treinamento, mas use-os para verificar a qualidade do treinamento. E se um e o mesmo trecho do mar caiu em duas imagens diferentes e ao mesmo tempo uma imagem caiu na sequência de treinamento e a outra na sequência de verificação, a verificação perderá o significado e a rede será treinada novamente, não verificaremos a capacidade da rede de generalizar informações, porque os dados são os mesmos. A luta contra esse fenômeno levou muito tempo e esforço da GPU dos participantes. Como de costume, os vencedores e os premiados não têm pressa em mostrar aos seus fãs os segredos da maestria e definir o código, e não há como estudá-lo e aprendê-lo, por isso vamos retomar a teoria.
Uma simples verificação visual mostrou que realmente há muitos dados, o mesmo trecho do mar caiu em fotos diferentes, veja os exemplos




É por esse motivo que não estamos interessados em dados reais, existem muitas dependências espúrias, conexões desnecessárias conosco, pouca marcação e outras deficiências.
No
primeiro artigo, vimos fotos com elipses e ruído e continuaremos a estudá-las. A vantagem dessa abordagem é que, se você encontrar algum recurso atraente de uma rede treinada em um conjunto arbitrário de imagens, não está claro se essa é uma propriedade de rede ou de um conjunto de treinamento. Os parâmetros estatísticos das seqüências retiradas do mundo real são desconhecidos. Recentemente, o grão-mestre Pleskov Pavel
paske57 falou sobre como às vezes é fácil obter uma classificação de segmentação / classificação de imagens, se é bom investigar os dados, por exemplo, veja os metadados das fotos. E não há garantias de que nos dados reais não existam tais dependências, deixadas involuntariamente. Portanto, para estudar as propriedades da rede, tiramos fotos com elipses e retângulos e determinamos o local, a cor e outros parâmetros usando um gerador de números aleatórios de um computador (que possui um gerador pseudo-aleatório, que possui um gerador baseado em outros algoritmos não digitais e propriedades físicas da substância, Mas não discutiremos isso neste artigo).
Portanto, pegue o mar
np.random.sample () * 0,75 , não precisamos de ondas, vento, costas e outros padrões e faces ocultos. Os navios / elipses também serão pintados da mesma cor e, para distinguir o mar do barco e da interferência, adicione 0,25 ao mar ou ao barco / jammer, e todos terão a mesma forma - elipses de diferentes tamanhos e orientações. A interferência também será apenas retângulos da mesma cor que a elipse - isso é importante, informações e interferência da mesma cor no contexto do ruído. Faremos apenas uma pequena alteração na coloração e executaremos
np.random.sample () para cada imagem e para cada elipse / retângulo, ou seja, Nem o plano de fundo nem a cor da elipse / retângulo são repetidos. Além disso, no texto, há um código do programa para criar figuras / máscaras e um exemplo de dez pares selecionados aleatoriamente.
Pegue uma versão muito comum da rede (você pode usar sua rede favorita) e tente identificar e mostrar a redundância de uma grande sequência de treinamento, para obter pelo menos algum tipo de características qualitativas e quantitativas de redundância. I.e. o autor acredita que muitos gigabytes de sequências de treinamento são substancialmente redundantes, existem muitas imagens desnecessárias, não há necessidade de carregar dezenas de GPUs e fazer cálculos desnecessários. A redundância de dados se manifesta não apenas e não tanto no fato de que as mesmas partes são exibidas em imagens diferentes, mas também na redundância de informações nesses dados. Os dados podem ser redundantes, mesmo que não sejam repetidos exatamente. Observe que essa não é uma definição estrita de informações e sua suficiência ou redundância. Queremos apenas descobrir o quanto você pode reduzir o trem, quais fotos você pode tirar da sequência de treinamento e quantas fotos são suficientes para um treinamento aceitável (definiremos a precisão no programa). Este é um programa específico, um conjunto de dados específico, e é possível que em elipses com triângulos, como obstáculo, nada funcione tão bem quanto em elipses com retângulos (minha hipótese é que tudo será o mesmo e o mesmo. Mas não estamos verificando agora) , não realizamos análises e não provamos teoremas).
Então, dado:
- sequência de aprendizado de pares de figuras / máscaras. Podemos gerar qualquer número de pares de imagens / máscaras. Responderei à pergunta imediatamente - por que a cor e o fundo são aleatórios? Responderei de forma simples, breve, clara e abrangente que gosto tanto, que não é necessária uma entidade extra na forma de uma borda;
- a rede é comum, U-net comum, ligeiramente modificada e amplamente utilizada para segmentação.
Idéia para testar:
- na sequência construída, como em tarefas reais, gigabytes de dados são usados. O autor acredita que o tamanho da sequência de treinamento não é tão crítico e não deve haver muitos dados, mas eles devem conter "muita" informação. Essa quantidade, dez mil pares de imagens / máscaras, não é necessária e a rede aprenderá com uma quantidade muito menor de dados.
Vamos começar, selecione 10.000 pares e considere-os com cuidado. Espremeremos toda a água, todos os pedaços desnecessários dessa sequência de treinamento, usaremos e colocaremos em prática todo o resíduo seco.
Agora você pode testar sua intuição e assumir quantos pares de 10.000 são suficientes para treinar e prever outro, mas também criou uma sequência de 10.000 pares com uma precisão de mais de 0,98. Escreva em um pedaço de papel, depois compare.
Para uso prático, leve em consideração que o mar e os navios com interferência são selecionados artificialmente, é
np.random.sample () .
Carregamos bibliotecas, determinamos os tamanhos de uma matriz de imagensimport numpy as np import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.optimizers import Adam from keras.layers import Input,Conv2D,Conv2DTranspose,MaxPooling2D,concatenate from keras.layers import BatchNormalization,Activation,Add,Dropout from keras.losses import binary_crossentropy from keras import backend as K import tensorflow as tf import keras as keras w_size = 128 train_num = 10000 radius_min = 10 radius_max = 20
determinar as funções de perda e precisão def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
Usaremos a métrica do
primeiro artigo . Deixe-me lembrar aos leitores que preveremos a máscara do pixel - este é o “mar” ou o “navio” e avaliaremos a verdade ou falsidade da previsão. I.e. As quatro opções a seguir são possíveis - previmos corretamente que um pixel é um "mar", previmos corretamente que um pixel é um "navio" ou cometemos um erro ao prever um "mar" ou um "navio". E assim, para todas as imagens e todos os pixels, estimamos o número das quatro opções e calculamos o resultado - este será o resultado da rede. E quanto menos previsões errôneas e mais verdadeiras, mais preciso o resultado e melhor a rede.
E para a pesquisa, vamos optar pela bem estudada U-net, que é uma excelente rede para segmentação de imagens. A opção U-net não tão clássica foi escolhida, mas a idéia é a mesma: a rede realiza uma operação muito simples com imagens - reduz a dimensão da imagem com algumas transformações passo a passo e tenta recuperar a máscara da imagem compactada. I.e. a dimensão da imagem em nosso caso é aumentada para 16x16 e, em seguida, tentamos restaurar a máscara usando dados de todas as camadas de compressão anteriores.
Examinamos a rede como uma “caixa preta”, não veremos o que acontece com a rede interna, como os pesos mudam e como os gradientes são escolhidos - esse é o tópico de outro estudo.
Rede em U com blocos def convolution_block(x, filters, size, strides=(1,1), padding='same', activation=True): x = Conv2D(filters, size, strides=strides, padding=padding)(x) x = BatchNormalization()(x) if activation == True: x = Activation('relu')(x) return x def residual_block(blockInput, num_filters=16): x = Activation('relu')(blockInput) x = BatchNormalization()(x) x = convolution_block(x, num_filters, (3,3) ) x = convolution_block(x, num_filters, (3,3), activation=False) x = Add()([x, blockInput]) return x
A função de gerar pares de imagem / máscara. Em uma imagem colorida de 128x128 preenchida com ruído aleatório com uma selecionada aleatoriamente em dois intervalos, 0,0 ... 0,75 ou 0,25..1,0. Coloque aleatoriamente uma elipse orientada aleatoriamente na imagem e coloque um retângulo no mesmo local. Verificamos que eles não se cruzam e, se necessário, deslocamos o retângulo para o lado. Cada vez que recalculamos os valores da coloração do mar / barco. Para simplificar, colocaremos a máscara com a imagem em uma matriz, como a quarta cor, ou seja, Red.Green.Blue.Mask, é mais fácil.
def next_pair(): img_l = (np.random.sample((w_size, w_size, 3))* 0.75).astype('float32') img_h = (np.random.sample((w_size, w_size, 3))* 0.75 + 0.25).astype('float32') img = np.zeros((w_size, w_size, 4), dtype='float') p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p1 = np.rint(np.random.sample()* (w_size-2*radius_max) + radius_max) p2 = np.rint(np.random.sample()* (w_size-2*radius_max) + radius_max) p3 = np.rint(np.random.sample()* (2*radius_max - radius_min) + radius_min) p4 = np.rint(np.random.sample()* (2*radius_max - radius_min) + radius_min) poly = np.array(( (p1, p2), (p1, p2+p4), (p1+p3, p2+p4), (p1+p3, p2), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc_rr = list(set(rr) & set(rr_p)) in_sc_cc = list(set(cc) & set(cc_p)) if len(in_sc_rr) > 0 and len(in_sc_cc) > 0: if len(in_sc_rr) > 0: _delta_rr = np.max(in_sc_rr) - np.min(in_sc_rr) + 1 if np.mean(rr_p) > np.mean(in_sc_rr): poly[:,0] += _delta_rr else: poly[:,0] -= _delta_rr if len(in_sc_cc) > 0: _delta_cc = np.max(in_sc_cc) - np.min(in_sc_cc) + 1 if np.mean(cc_p) > np.mean(in_sc_cc): poly[:,1] += _delta_cc else: poly[:,1] -= _delta_cc rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img[:,:,:3] = img_l.copy() img[rr, cc,:3] = img_h[rr, cc] img[rr_p, cc_p,:3] = img_h[rr_p, cc_p] else: img[:,:,:3] = img_h.copy() img[rr, cc,:3] = img_l[rr, cc] img[rr_p, cc_p,:3] = img_l[rr_p, cc_p] img[:,:,3] = 0. img[rr, cc,3] = 1. return img
Vamos criar uma sequência de treinamento de pares, veja aleatoriamente 10
_txy = [next_pair() for idx in range(train_num)] f_imgs = np.array(_txy)[:,:,:,:3].reshape(-1,w_size ,w_size ,3) f_msks = np.array(_txy)[:,:,:,3:].reshape(-1,w_size ,w_size ,1) del(_txy)
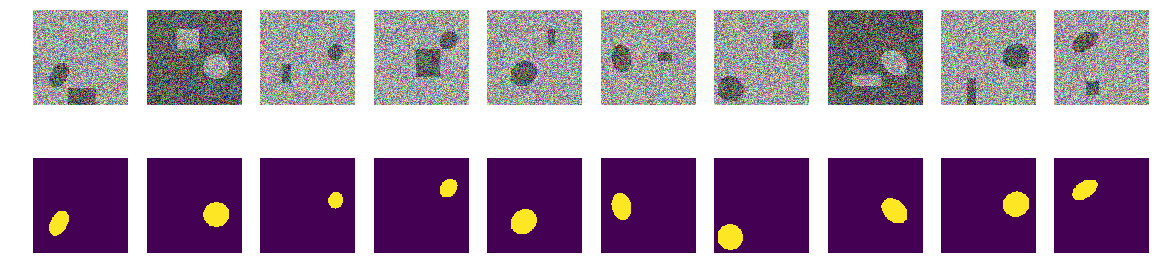
Primeiro passo Vamos tentar treinar em um conjunto mínimo
O primeiro passo de nosso experimento é simples: estamos tentando treinar a rede para prever apenas 11 primeiras fotos.
batch_size = 10 val_len = 11 precision = 0.85 m0_select = np.zeros((f_imgs.shape[0]), dtype='int') for k in range(val_len): m0_select[k] = 1 t = tqdm() while True: fit = model.fit(f_imgs[m0_select>0], f_msks[m0_select>0], batch_size=batch_size, epochs=1, verbose=0 ) current_accu = fit.history['my_iou_metric'][0] current_loss = fit.history['loss'][0] t.set_description("accuracy {0:6.4f} loss {1:6.4f} ".\ format(current_accu, current_loss)) t.update(1) if current_accu > precision: break t.close()
accuracy 0.8636 loss 0.0666 : : 47it [00:29, 5.82it/s]Selecionamos os 11 primeiros da sequência inicial e treinamos a rede neles. Agora, não importa se a rede memoriza essas imagens especificamente ou resume, o principal é que ela possa reconhecer essas 11 fotos da maneira que precisamos. Dependendo do conjunto de dados e da precisão selecionados, o treinamento em rede pode durar muito, muito tempo. Mas temos apenas algumas iterações. Repito que agora não é importante para nós como e o que a rede aprendeu ou aprendeu, o principal é que atingiu a precisão estabelecida da previsão.
Agora comece o experimento principal
Tiraremos novos pares de foto / máscara da sequência construída e tentaremos predizê-los pela rede treinada na sequência já selecionada. No começo, são apenas 11 pares de imagem / máscara e a rede é treinada, talvez não muito corretamente. Se em um novo par a máscara da imagem é prevista com precisão aceitável, descartamos esse par, ele não possui novas informações para a rede, ele já sabe e pode calcular a máscara dessa imagem. Se a precisão da previsão for insuficiente, adicionamos esta imagem com uma máscara à nossa sequência e começamos a treinar a rede até que um resultado de precisão aceitável seja alcançado na sequência selecionada. I.e. Esta imagem contém novas informações e as adicionamos à nossa sequência de treinamento e extraímos as informações nele contidas pelo treinamento.
batch_size = 50 t_batch_size = 1024 raw_len = val_len t = tqdm(-1) id_train = 0
Accuracy 0.9830 loss 0.0287 selected img 271 tested img 9949 : : 1563it [14:16, 1.01it/s]
Aqui, a precisão é usada no sentido de "precisão", e não como a métrica keras padrão, e a sub-rotina "my_iou_metric" é usada para calcular a precisão. É muito interessante observar a precisão e o número de imagens investigadas e adicionadas. No início, quase todos os pares de imagens / máscaras são adicionados pela rede e, em torno de 70, ela começa a ser descartada. Mais perto de 8000 joga quase todos os pares.
Verifique pares visualmente aleatórios selecionados pela rede:
fig, axes = plt.subplots(2, 10, figsize=(20, 5)) t_imgs = f_imgs[m0_select>0] t_msks = f_msks[m0_select>0] for k in range(10): kk = np.random.randint(t_msks.shape[0]) axes[0,k].set_axis_off() axes[0,k].imshow(t_imgs[kk]) axes[1,k].set_axis_off() axes[1,k].imshow(t_msks[kk].squeeze())
Nada de especial ou sobrenatural:
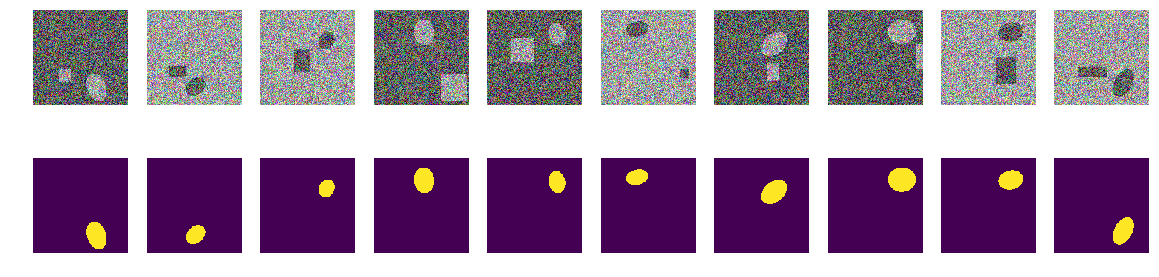
Estes são pares selecionados pela rede em diferentes estágios do treinamento. Quando a rede recebeu um par de entrada dessa sequência, não foi possível calcular a máscara com a precisão especificada e esse par foi incluído na sequência de treinamento. Mas nada de especial, fotos comuns.
Verificação de resultado e precisão
Verificaremos a qualidade do programa de treinamento em rede, garantiremos que a qualidade não dependa significativamente da ordem da sequência inicial, para a qual misturamos a sequência inicial de pares de foto / máscara, pegamos os outros 11 primeiro e da mesma maneira, treinamos a rede e eliminamos o excesso.
sh = np.arange(train_num) np.random.shuffle(sh) f0_imgs = f_imgs[sh] f0_msks = f_msks[sh] model.compile(loss=bce_dice_loss, optimizer="adam", metrics=[my_iou_metric]) model.summary()
Código do treino batch_size = 10 val_len = 11 precision = 0.85 m0_select = np.zeros((f_imgs.shape[0]), dtype='int') for k in range(val_len): m0_select[k] = 1 t = tqdm() while True: fit = model.fit(f0_imgs[m0_select>0], f0_msks[m0_select>0], batch_size=batch_size, epochs=1, verbose=0 ) current_accu = fit.history['my_iou_metric'][0] current_loss = fit.history['loss'][0] t.set_description("accuracy {0:6.4f} loss {1:6.4f} ".\ format(current_accu, current_loss)) t.update(1) if current_accu > precision: break t.close()
accuracy 0.8636 loss 0.0710 : : 249it [01:03, 5.90it/s]
batch_size = 50 t_batch_size = 1024 raw_len = val_len t = tqdm(-1) id_train = 0
Accuracy 0.9890 loss 0.0224 selected img 408 tested img 9456 : : 1061it [21:13, 2.16s/it]
O resultado não depende significativamente da ordem dos pares da sequência original. No caso anterior, a rede escolheu 271, agora 408, se você ainda misturar, a rede poderá escolher uma quantidade diferente. Não vamos verificar, o autor acredita que sempre haverá substancialmente menos de 10.000.
Verifique a precisão da previsão de rede em uma nova sequência independente
_txy = [next_pair() for idx in range(train_num)] test_imgs = np.array(_txy)[:,:,:,:3].reshape(-1,w_size ,w_size ,3) test_msks = np.array(_txy)[:,:,:,3:].reshape(-1,w_size ,w_size ,1) del(_txy) test_pred_0 = model.predict(test_imgs) t_val_0 = get_iou_vector(test_msks,test_pred_0) t_val_0
0.9927799999999938
Resumo e Conclusões
Assim, conseguimos extrair menos de trezentos ou quatrocentos selecionados entre 10.000 pares, a precisão da previsão é de 0,99278, pegamos todos os pares que contêm pelo menos algumas informações úteis e jogamos fora o resto. Não alinhamos os parâmetros estatísticos da sequência de treinamento, adicionamos repetibilidade de informações, etc. e não usou métodos estatísticos. Tiramos uma foto que contém informações ainda desconhecidas da rede e compactamos tudo com o peso da rede. Se a rede encontrar pelo menos uma imagem “misteriosa”, ela usará tudo nos negócios.
Um total de 271 pares de figuras / máscaras contém informações para prever 10.000 pares com uma precisão de pelo menos 0,8075 em cada par, ou seja, a precisão total de toda a sequência é maior, mas em cada figura não é inferior a 0,8075, não temos imagens que não temos podemos prever e conhecemos o limite inferior dessa previsão. (é claro que aqui o autor se vangloriava de que, sem isso, o artigo não verifica essa afirmação, cerca de 0,8075, ou evidência, mas provavelmente isso é verdade)
Para o treinamento em rede, não há necessidade de carregar a GPU com tudo o que está disponível, você pode retirar o núcleo do trem e treinar a rede nele como o início do treinamento. À medida que obtém novas fotos, você pode marcar manualmente aquelas que a rede não pôde prever e adicioná-las ao núcleo do trem, treinando novamente a rede para extrair todas as informações das novas fotos. E não é necessário destacar uma sequência de validação; podemos assumir que tudo o resto, exceto o selecionado, é uma sequência de validação.
Mais uma observação matematicamente não estrita, mas muito importante. É seguro dizer que cada par de foto / máscara contém "muita" informação. Cada par contém "muita" informação, embora na maioria dos pares imagem / máscara a informação se cruze ou se repita. Cada um dos 271 pares de figura / máscara contém informações essenciais para a previsão e esse par não pode ser simplesmente jogado fora.
Bem, uma pequena observação sobre dobras, muitos especialistas e praticantes de kagglers dividem a sequência de treinamento em dobras e treinam-nas separadamente, combinando os resultados obtidos de maneiras mais complicadas. No nosso caso, você também pode dividi-lo em dobras. Se você remover 271 pares de 10.000, poderá criar uma nova sequência raiz nos restantes, o que obviamente fornecerá um resultado diferente, mas comparável. Você pode simplesmente misturar e pegar os outros 11 iniciais, como mostrado acima.
O artigo fornece um código e mostra como treinar U-net para segmentação de imagens. Este é um exemplo concreto e, no artigo, intencionalmente, não há generalizações para outras redes, para outras seqüências, não há matemática rigorosa, tudo é dito e mostrado "nos dedos". Apenas um exemplo de como você pode aprender a rede enquanto obtém uma precisão aceitável.