Olá.
No meu artigo anterior, falei sobre como fiz
animação dos planetas do sistema solar para meu filho. Obrigado a todos pelo feedback e pelas calorosas boas-vindas. Hoje eu preparei algumas animações mais interessantes, unidas condicionalmente sob o tema "movimento circular e oscilações". Em outras palavras, o que é descrito por cossenos e senos.

Para renderização, usei javascript e canvas. Para cada exemplo, é fornecido um link onde você pode observar cuidadosamente tudo. Você pode olhar o código fonte, pode copiar a si mesmo - não me importarei. O material pode muito bem ser útil em aulas e disciplinas eletivas em física, matemática ou ciência da computação.
Então vamos lá.
Trajectória da lua
Vamos começar com a mecânica celeste. Minha pergunta favorita para crianças em idade escolar: “A Terra se move [quase] em um círculo ao redor do Sol e a Lua - em um círculo ao redor da Terra. Como é a trajetória da lua no quadro de referência do sol? ” Espero que os queridos leitores estejam mais preparados e não comecem a desenhar esses "cachos":
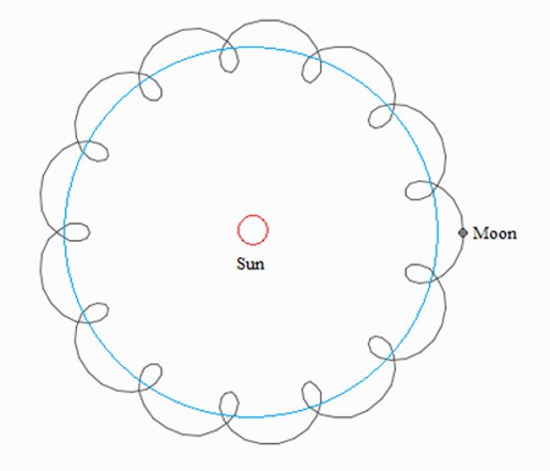
Embora essa trajetória se encaixe no senso comum, ela não ocorre especificamente com a Lua. De fato, a Terra "corre" em órbita, e a Lua, como anexada, é levemente esquerda ou levemente direita. De fato: a velocidade orbital da Terra é de ~ 30 km / s, da Lua - cerca de 1 km / s. Obviamente, a velocidade da lua não é suficiente para se mover na direção oposta. Uma explicação mais precisa está associada ao cálculo das forças que atuam na Lua (do lado da Terra e do Sol) e para onde o raio de curvatura da trajetória é direcionado (deixarei isso para um estudo independente).
Então, em teoria, parece estar claro. Mas ainda há algum eufemismo. Eu quero ver como realmente é. Vamos fazer um
modelo em uma escala de 1 pixel = 30.000 km. Esta é uma opção de compromisso para que as órbitas sejam distinguíveis, embora a escala da imagem ainda seja enorme: 15000 * 15000 pixels. Na animação, o movimento da Terra e da Lua é descrito pelas leis do movimento circular: uma trajetória azul para a Terra e preto para a Lua. Após desenhar, você pode ver o resultado. Pode-se ver quão pequenos são os desvios totais da órbita da Lua em relação à órbita da Terra. Aqui está um exemplo de um pequeno fragmento de uma imagem:

Para que os desenhos na Internet sejam extremamente distorcidos, você precisa se lembrar disso.
A propósito, por uma questão de interesse, você pode fazer a mesma animação com algum satélite de Júpiter. Em teoria, já deveria haver "cachos".
Figuras de Lissajous
Era uma vez, quando eu estava estudando na escola de educação física de Novosibirsk, tivemos o trabalho de laboratório "Figuras de Lissajous", como deveria ser, com geradores e um osciloscópio soviético. Parecia completo e interessante. Dependendo das frequências dos sinais fornecidos às entradas, várias formas são obtidas na tela do osciloscópio:
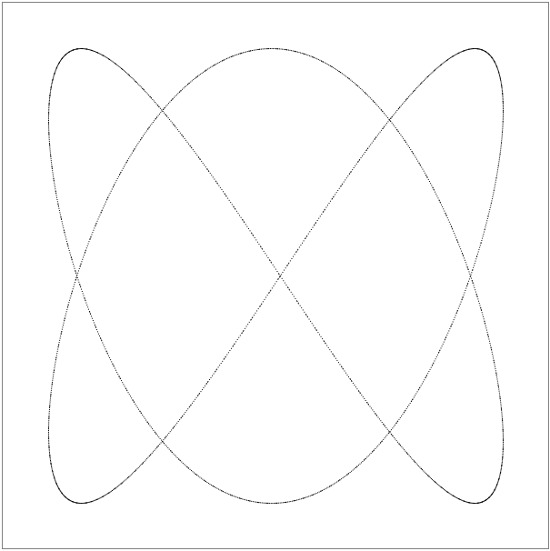
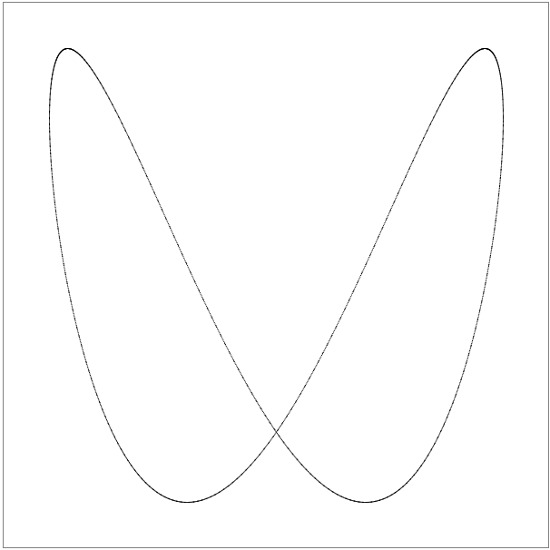
De fato, cada figura é a adição de duas vibrações simultâneas - ao longo do eixo X e ao longo do eixo Y. As frequências dessas vibrações podem ser correlacionadas como 1: 1 (uma oscilação ao longo de X, uma ao longo de Y; um círculo, elipse ou linha reta pode ser obtida), 1: 2 (um em X, dois em Y; uma parábola ou "sela" é obtida), 1: 3, 2: 3 (figuras mais complexas) e assim por diante - acho que você entende o princípio. Você pode encontrar uma base teórica detalhada na
Wikipedia , e eu preparei uma
página separada onde você pode "brincar" com diferentes coeficientes.
Um parâmetro interessante é a mudança de fase entre as oscilações. Se for continuamente alterado, a figura "ganha vida" - começa a girar. Aqui, minha pergunta favorita é: "e em que direção ele gira?" Alguém diz que em uma direção, alguém - na outra, mas em geral você pode "mudar" a direção da rotação em movimento. Isso é puramente uma questão de percepção. Experimente e faça.
Nós complicamos nossa animação adicionando
atenuação a ela . Nesse caso, o ponto “cai” gradualmente para o centro, mas, novamente, ao longo de uma trajetória complexa e bastante bonita.

A propósito, isso pode ser feito ao vivo. Conforme recomendado em um livro, você precisa fazer um cilindro com um pequeno orifício na parte inferior, despejar a sêmola ali, pendurá-lo na porta e balançar. A sêmola de esvaziamento irá apenas desenhar a figura esbatida de Lissajous.
Spirograph
Um brinquedo das lembranças da infância, quando eu, com 6-7 anos de idade, pintei padrões visitando minha avó:

Se de repente alguém, por alguma coincidência inédita, não estiver familiarizado com esse milagre, corra para a
Wikipedia . Veremos a página de
animação . Existem apenas três parâmetros, como em um espirógrafo real: o raio do círculo pequeno / grande e a distância do ponto ao centro do círculo pequeno. Mas suas diferentes combinações fornecem um grande número de padrões (exemplos que você viu no início deste artigo).
A propósito, o script revelou uma característica interessante: nele você pode definir combinações que são simplesmente impossíveis em um espirógrafo real - por exemplo, aumentar o
círculo interno que o externo , ou até mesmo
fazer o buraco fora do círculo interno . O programa permite que você invente o que quiser.
Resultados
Vamos resumir. Como você pode ver, nossas animações estão na junção da física e da ciência da computação. É bom e interessante ler sobre a Lua ou as mesmas figuras de Lissajous, mas é duplamente bom e interessante vê-lo na tela e "brincar" com os parâmetros. Obviamente, se houver objetos reais para obter o resultado, é claro que você precisará usá-lo (por exemplo, dispositivos eletrônicos - geradores, um osciloscópio - para observar as figuras de Lissajous). Geralmente sou um defensor do "trabalho com as mãos". Mas muitas vezes não há nada adequado - nesses casos, a animação no computador ajuda.
Eu também gostaria de observar separadamente o componente estético. A natureza, em minha convicção pessoal, é incrivelmente bela em sua essência. Concordo, é bom olhar para uma fórmula curta e simples que descreva toda uma classe de fenômenos. Ou, novamente, para uma representação gráfica de alguma fórmula (como em um espirógrafo). E, por exemplo, as linhas do campo magnético? E o resultado de colisões de partículas? Lembro-me que na universidade também desenhávamos soluções de equações diferenciais - até havia graça e beleza. Se você sabe tudo isso e entende do que estou falando, vamos apertar a mão um do outro. E se agora você está interessado nisso, para você tudo está apenas começando. Hoje foi o primeiro passo.