Genética da cultivar Romanesco: um modelo matemático fractal de expressão gênica

O que flocos de neve, repolho Romanesco, estrela do mar, raios e árvores têm em comum? Você não dirá imediatamente, mas do ponto de vista matemático, todos esses objetos têm uma característica em comum: a fratalidade. Aos olhos da matemática, tudo em nosso mundo obedece às leis da "Rainha das Ciências". Qualquer fenômeno, processo ou objeto pode ser expresso em forma matemática, o que permite que seja analisado sob um novo ângulo, por assim dizer. Por muitos anos, os cientistas tentam criar a representação matemática perfeita dos genes, seus relacionamentos e os processos em que estão envolvidos. Hoje falaremos sobre como os fractais ajudaram a estabelecer as bases para um modelo matemático completamente novo de genes humanos da perspectiva do câncer. O que é um fractal, por que é tão importante para geneticistas e matemáticos, e como um novo modelo matemático pode ajudar a medicina moderna? Procuraremos respostas no relatório do grupo de pesquisa. Vamos lá

Retiro teórico

Para começar, vale a pena descobrir brevemente o que é um fractal e o que é comido.

Um fractal é um conjunto com propriedades de auto-similaridade. Simplificando, quando algo consiste em várias mini-cópias de si mesmo.



Os fractais são encontrados em vários fenômenos físicos: da difusão à turbulência. Isso pode ser chamado de manifestações naturais de fractais. As pessoas também descobriram o uso de fractais: em computação gráfica, engenharia de rádio, tecnologias de rede, etc.

Os fractais são muito coloridos no filme “Doutor Estranho” (2016), quando o Ancião envia o protagonista em uma excursão por dimensões paralelas.


Uma visão um pouco desagradável, mas claramente demonstrando fratalidade.

Mesmo nas prateleiras do supermercado, você pode encontrar manifestações de fraturamento, a exemplo do repolho ou couve-flor Romanesco.

Se levarmos em conta que existem muitos tipos de conjuntos com propriedades fractais, pode-se argumentar que quase tudo ao nosso redor está, de uma maneira ou de outra, conectado a fractais. E o corpo humano, especialmente seus genes, não é exceção. Como os fractais podem ser matematicamente explicados pela classificação dos componentes, o uso desse modelo em genes humanos pode ajudar significativamente na compreensão dos vários processos que ocorrem em nosso corpo, incluindo várias doenças, patologias e outras coisas desagradáveis.

Um dos processos mais importantes em nosso corpo é a expressão gênica (imagem 1a ), quando a informação hereditária dos genes é transformada em um produto funcional. Em outras palavras, nossas células através da expressão gênica controlam sua estrutura e função. Nossos genes são um banco de dados do qual todas as células do corpo derivam informações, desempenhando as funções necessárias a partir de então. Portanto, nossa boca não produz pêlos, o sistema imunológico combate infecções, as células sanguíneas transportam oxigênio, etc. Todos esses processos ocorrem precisamente devido à programação das células para executar tarefas específicas, que por sua vez são possíveis através da síntese de proteínas a partir da ativação de um gene em particular.


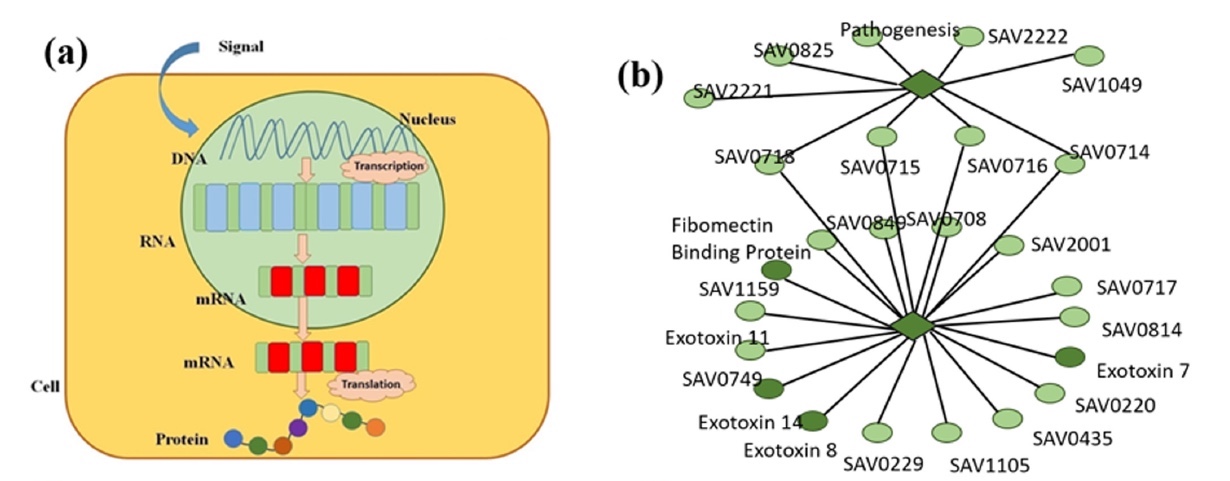Imagem Nº 1

A regulação da expressão gênica indica quando, quanto e por quanto tempo determinadas proteínas devem ser produzidas. Portanto, o estudo desse processo é de grande importância para uma compreensão completa de como funcionam certos mecanismos de controle de organismos.

Esse processo complexo é importante para os cientistas, pois, tendo a oportunidade de controlá-lo, eles serão capazes de criar certas células sintéticas dotadas de funções claras, em particular a entrega de medicamentos contra o câncer ao próprio “coração” da doença para um tratamento mais eficaz.

Para melhorar os métodos de tratamento de tais doenças, é necessário aprender o aspecto genético com mais detalhes. Para fazer isso, os cientistas propõem apresentar o corpo humano na forma de um programa, onde os genes agem como linhas de código que podem ser alteradas se o programa funcionar com um mau funcionamento. Para perceber isso, você deve primeiro criar um modelo matemático do gene. No momento, esses modelos já existem, mas não podem ser representativos porque visavam estudar a dinâmica da rede de genes. Nesse mesmo estudo, que aplicou o conceito de fractais, os cientistas decidiram se concentrar no processo de expressão de um gene em particular e, em seguida, aplicar a correlação cruzada entre os pares gene- FT * ( 1b ).

O fator de transcrição (FT) * é uma proteína de controle de síntese de mRNA que contém informações sobre a estrutura primária de proteínas na matriz de DNA, através da ligação a locais específicos de DNA.

Simplificando, os cientistas decidiram se aprofundar um pouco mais, tendo examinado não toda a “parede” como um todo, mas os “tijolos” individuais.

Resultados da pesquisa

Os sujeitos deste estudo foram o fungo Saccharomyces cerevisiae (levedura de padeiro) e a bactéria Escherichia coli (Escherichia coli).

Analisando os dados estatísticos da expressão genética dos sujeitos experimentais, foi calculado o coeficiente de Hurst * .

O coeficiente de Hurst * é uma medida da análise de séries temporais.

Séries temporais * - um conjunto de dados estatísticos coletados em diferentes intervalos de tempo sobre um indicador.

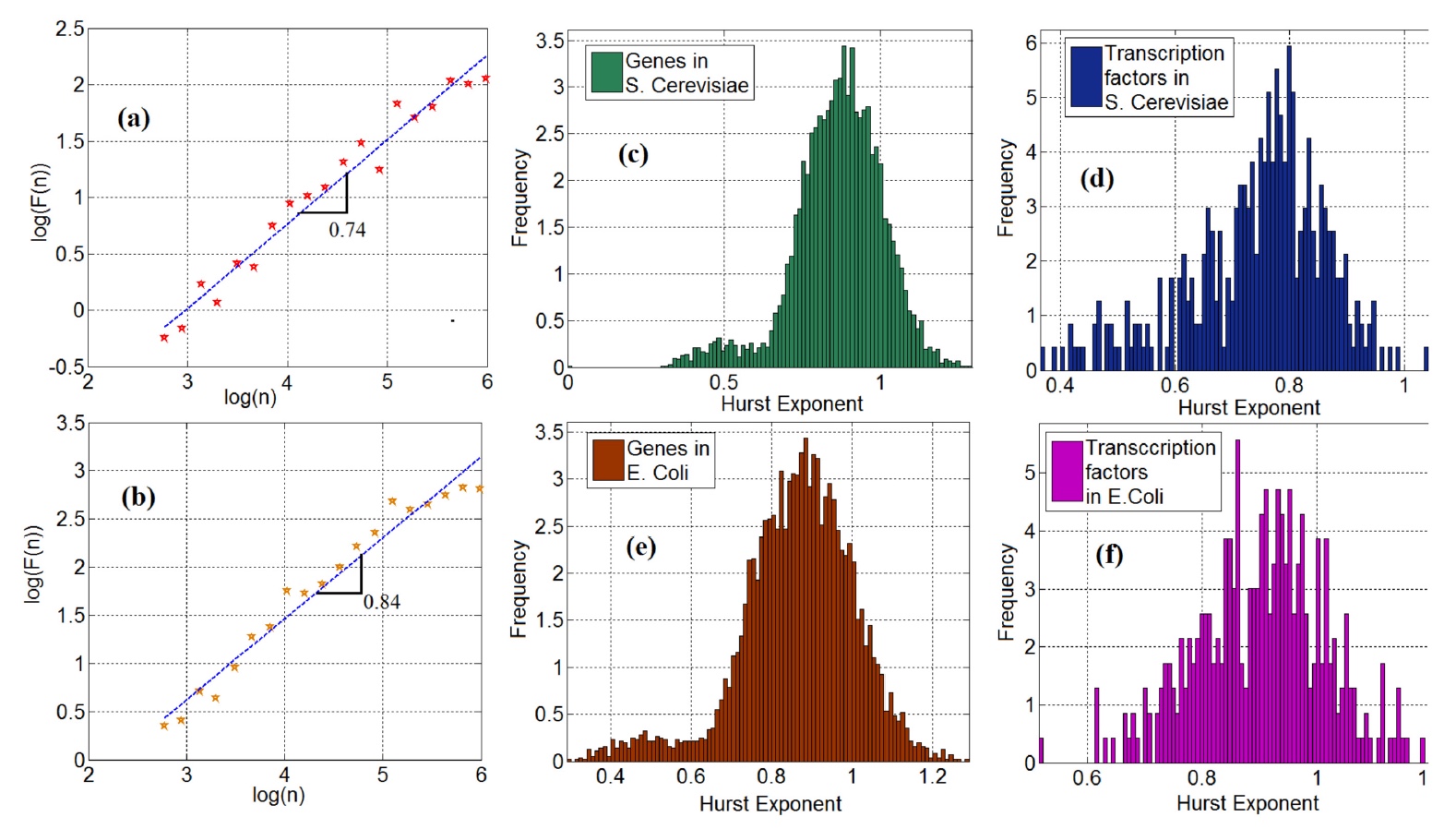Imagem No. 2

As figuras 2a (levedura) e 2b (Escherichia coli) mostram gráficos bilogarítmicos * de flutuações em função da escala da série temporal do TF.

O gráfico bilogarítmico * é um gráfico de dados bidimensional usando uma escala logarítmica nos dois eixos (vertical e horizontal).

A inclinação da curva nesses gráficos corresponde ao coeficiente de Hurst. Vale ressaltar que 95% (levedura) e 98% (bacilo) das séries temporais de genes apresentaram dependência em longo prazo * .

Dependência a longo prazo * - um indicador na análise de séries temporais, indicando a atenuação lenta da dependência estatística de dois pontos, com um aumento no intervalo de tempo entre eles. É determinado pelo indicador do coeficiente Hurst - de 0 a 1. Se o indicador estiver acima de 0,5, teremos uma forte relação de longo prazo, abaixo de 0,5 - o efeito oposto.

O coeficiente de Hurst de dependência de longo prazo nesse caso em particular foi de 0,5, o que indica sua ausência, em teoria. Entretanto, análises adicionais dos dados mostraram que esse indicador excede um valor de 0,5, o que indica a presença de uma dependência de longo prazo da série temporal na expressão genética ( 2c e 2e ). Isso sugere que a série temporal do gene-FT não pode ser considerada algo aleatório, portanto deve ser modelada com base na cadeia de Markov, quando houver uma série de eventos, cuja aleatoriedade depende de cada evento anterior.

Como os genes, os fatores de transcrição também mostraram uma relação de longo prazo: 97% para leveduras e bacilos (gráficos 2d e 2f ).

Agora adicione uma pitada de análise fractal à tigela comum. Para começar, os cientistas chamam nossa atenção para a bimodalidade da distribuição do coeficiente de Hurst. Isso é melhor observado nos gráficos 2c e 2e. Os cientistas explicam essa observação pelo fato de que existem processos de difusão na expressão gênica que têm vários potenciais de difusão. Portanto, a bimodalidade pode ser explicada pelo movimento browniano sem equilíbrio com potenciais diferentes. Mas essa afirmação requer evidências adicionais, que os cientistas procurarão nos seguintes estudos.

E agora retornaremos à multifractalidade. Os cientistas usaram análises multifractais das flutuações detrendas para determinar a presença / ausência de características multifractais em séries temporais de expressão gênica. Esta análise mostrou a presença de ambos os genes e a TF.

Os cientistas também aplicaram a metodologia bootstrap * para determinar com precisão (mais precisamente, para confirmar) a presença de dependência a longo prazo, dados os comprimentos limitados das séries temporais experimentais.

Bootstrap * - uma técnica para analisar estatísticas de distribuições de probabilidade.

Para cada série temporal de expressão gênica, 10 subintervalos aleatórios foram preparados, cada um contendo 90% do fragmento ordenado da série temporal inicial. Além disso, para todas as opções, o coeficiente de Hurst foi calculado. Assim, a diferença foi obtida entre os indicadores das séries temporais experimentais e versões aleatórias. Para E. coli, a diferença foi de apenas 0,006%, e para levedura de padaria ainda menor - 0,0001%. Assim, a presença de dependência a longo prazo em ambas as amostras foi confirmada.

Depois de considerar as características do gene e da TF separadamente que são de interesse, os cientistas começaram a analisar os pares gene-TF como um único objeto. O cálculo do índice de correlação cruzada mostrou que 98% dos pares gene-FT (em ambas as amostras) possuem propriedades de dependência a longo prazo ( 3a ).


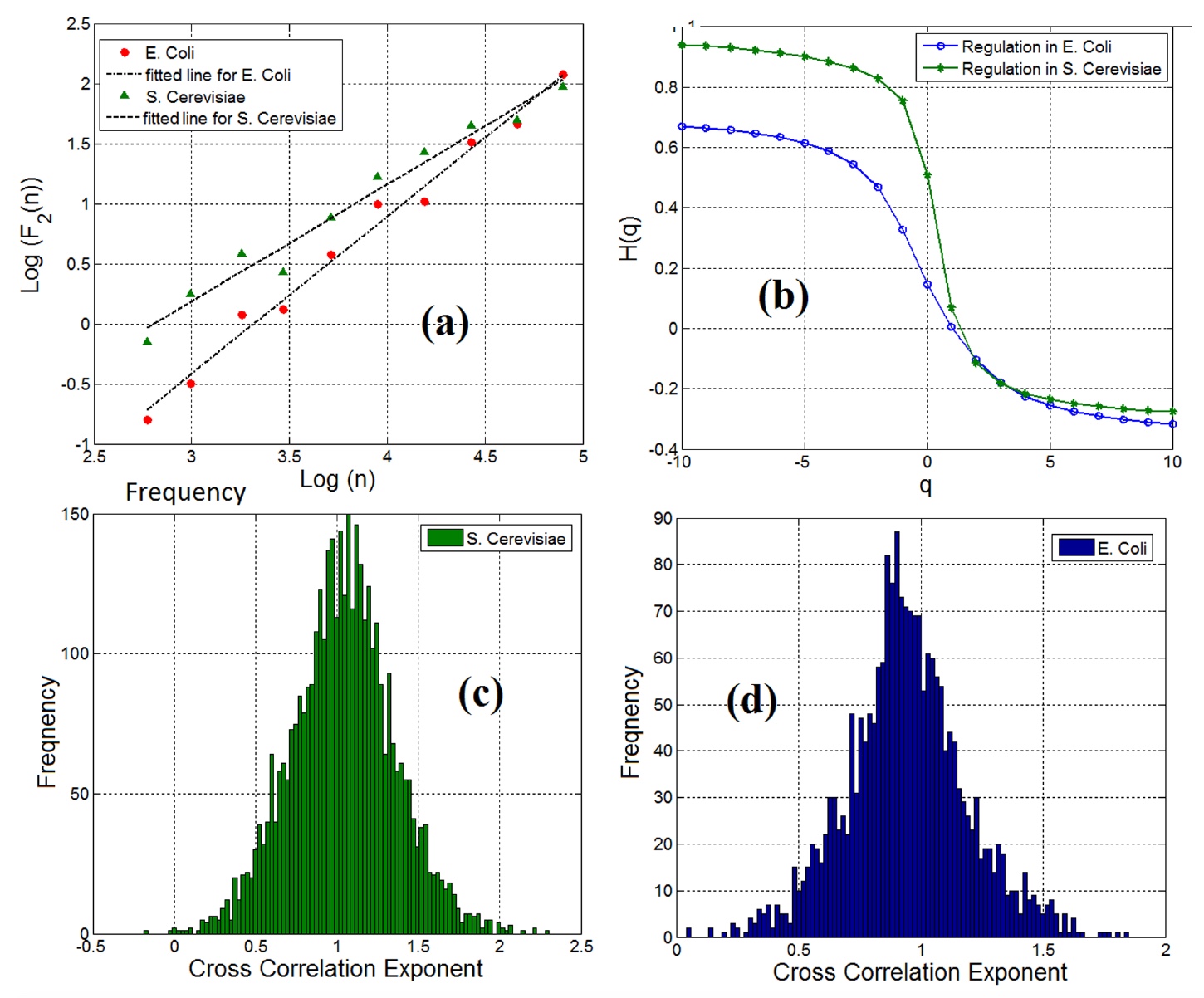Imagem No. 3

Uma análise multifractal das flutuações detrend confirmou a presença de características multifractais nos pares gene-FT (gráfico 3b ).

Vale ressaltar que, independentemente do fato de que tanto a correlação cruzada fractal quanto a longo prazo foram observadas em pares de genes e fatores de transcrição nas redes de regulação de genes, a correlação cruzada não foi a mesma para todos os pares. Os gráficos 3c (levedura) e 3d (Escherichia coli) mostram a correlação cruzada dos pares gene-FT.

Os cientistas usaram esses gráficos para medir a entropia informacional e, como resultado, o conteúdo informacional da rede de regulação de genes para vários tipos de células para análise quantitativa e especificação de redes de regulação de genes.Os indicadores de entropia foram: 4.18 - levedura, 5.29 - E. coli. E isso sugere que a rede de expressão gênica no fermento de padeiro é muito maior e mostra uma dinâmica mais complexa do que a rede de expressão gênica em Escherichia coli.

E agora o mais interessante é a criação de um modelo matemático. Os cientistas escolheram duas versões do modelo: o conjunto de Mandelbrot e o conjunto na forma de árvores diádicas wavelet.

Usando os indicadores obtidos anteriormente do coeficiente de Hölder no espectro multifractal, os cientistas descobriram que apenas 0,04 de todos os pares de gene-FT na rede de regulação de genes de levedura do padeiro podem ser modelados usando o conjunto de Mandelbrot. E em E. coli, nem um único par pode ser modelado por esse método.

Se considerarmos os pares que foram capazes de simular, houve uma enorme discrepância nos dados entre o modelo e as observações experimentais. Como conclusão, o método de modelagem devido ao conjunto de Mandelbrot não é adequado.


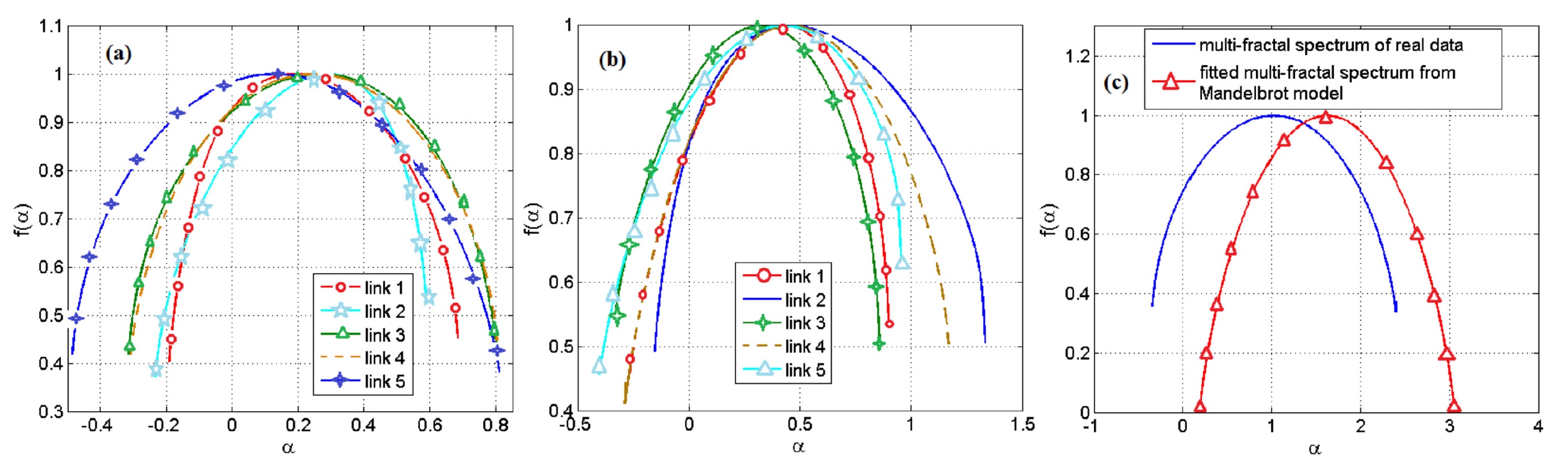Imagem No. 4

Os resultados do uso do modelo baseado no conjunto de Mandelbrot são mostrados nos gráficos acima. O mais brilhante é 4c , onde podemos ver quanto os dados divergem.

Os cientistas também compararam a multifractalidade observada de interdependências na rede de regulação de genes e o modelo multifractal de cascatas aleatórias em árvores diádicas de wavelets.

Os pesquisadores decidiram verificar se o modelo logarítmico da cascata W é adequado para a representação de pares gene-FT em redes de regulação de genes. Com base no espectro empírico e no espectro de singularidades, os parâmetros deste modelo foram calculados. Em seguida, foram feitos cálculos das áreas de interseção dos espectros multifractais calculados e empíricos, cuja razão se tornou o principal critério para aceitar ou rejeitar esse modelo matemático multifractal.


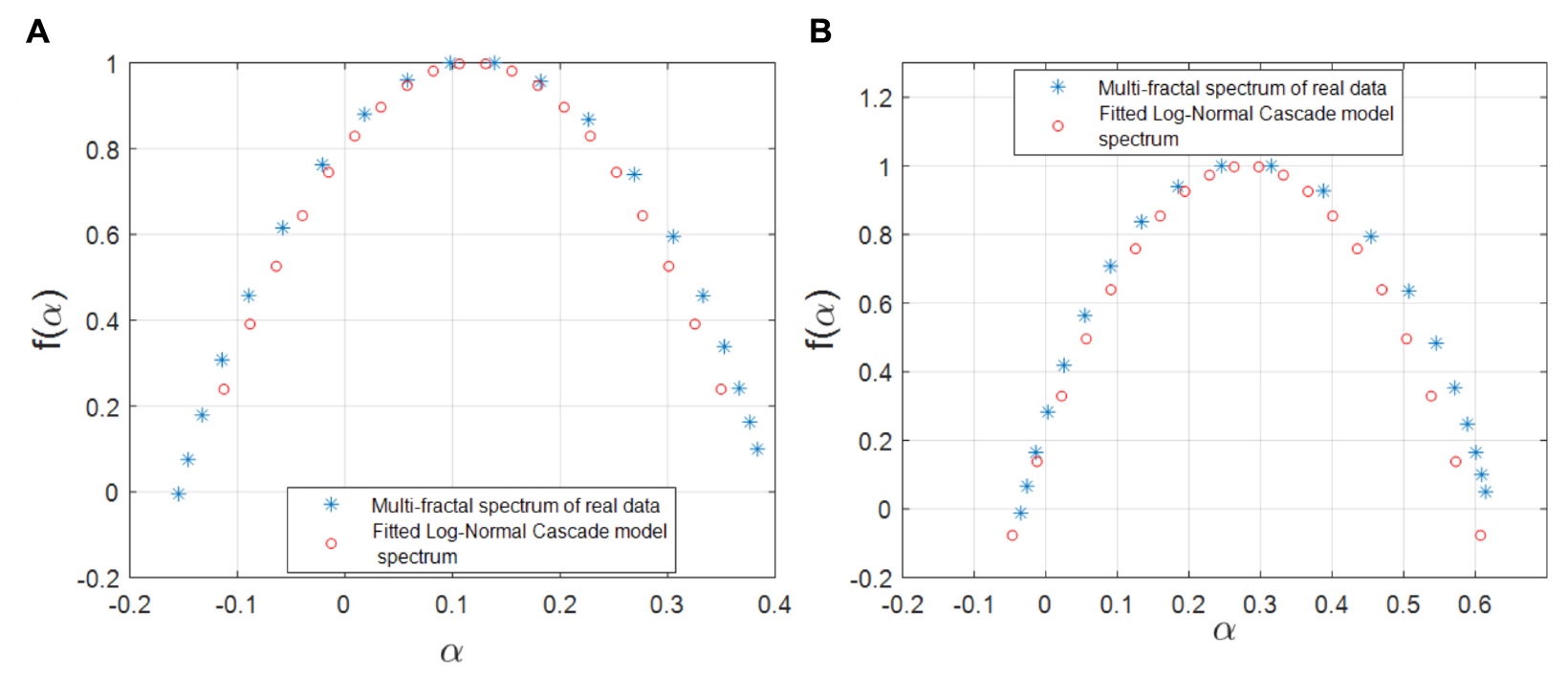Imagem No. 5

Como pode ser visto nos gráficos acima, demonstrando os espectros multifractais simulados e empíricos, este modelo está quase completamente correlacionado com os dados de observações e cálculos realizados anteriormente.

Para um conhecimento mais detalhado das nuances do estudo, recomendo que você analise o relatório do grupo de pesquisa neste link .

Epílogo

Este estudo, sendo principalmente teórico, possui grande potencial para uso prático, pois ajudou a modelar matematicamente a rede de regulação da expressão gênica - um dos processos mais importantes em qualquer organismo vivo. Processos complexos são difíceis de entender, por mais estranho que pareça. Para facilitar a tarefa, é necessário dividir o processo em componentes, elaborar seus “mapas” e seguir a rota desejada, observando todas as características e características importantes. A modelagem matemática, como nada mais, é ótima para isso. Tendo estudado o modelo matemático de um objeto ou processo, podemos entender com o que estamos lidando antes de prosseguir com o estudo do objeto ou processo real.

Este estudo confirmou mais uma vez que não apenas a física e a química dominam o mundo, mas a matemática está longe de ser o último lugar no Olimpo das ciências.

Obrigado pela atenção, continuem curiosos e tenham uma ótima semana de trabalho, pessoal.

Obrigado por ficar conosco. Você gosta dos nossos artigos? Deseja ver materiais mais interessantes? Ajude-nos fazendo um pedido ou recomendando a seus amigos, um desconto de 30% para os usuários da Habr em um análogo exclusivo de servidores básicos que inventamos para você: Toda a verdade sobre o VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps da US $ 20 ou como dividir o servidor? (as opções estão disponíveis com RAID1 e RAID10, até 24 núcleos e até 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps até 1º de janeiro de graça, se pago por um período de seis meses, você pode fazer o pedido aqui .

Dell R730xd 2 vezes mais barato? Somente nós temos 2 TVs Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 a partir de US $ 249 na Holanda e nos EUA! Leia sobre Como criar um prédio de infraestrutura. classe usando servidores Dell R730xd E5-2650 v4 custando 9.000 euros por um centavo?