Matemático amador descobriu a menor cobertura universal

Através de cálculos geométricos difíceis, Philip Gibbs descobriu o menor revestimento conhecido para qualquer forma possível.

Uma cobertura universal como um hexágono pode ser descrita em qualquer forma.

Philip Gibbs não é um matemático profissional. Portanto, quando ele queria refletir sobre uma tarefa, procurava uma que um amador pudesse lidar. Ele descobriu uma tarefa difícil que pode enlouquecer até as melhores mentes. E em um artigo publicado este ano, Gibbs fez progressos significativos na resolução da questão de cem anos atrás, dependendo da capacidade de medir com precisão a área até escalas atômicas.

O primeiro a propor esse problema foi o matemático francês Henri Leon Lebesgue, em uma carta a seu amigo Julius Pal, escrita em 1914. Lebesgue perguntou: qual é o formato da menor área possível, capaz de cobrir completamente um grande número de outras formas (possuindo uma propriedade comum, descrita abaixo)?

No século passado, a tarefa de encontrar uma cobertura universal se transformou em uma ratoeira: o progresso em resolvê-la, se acontecesse periodicamente, sempre foi surpreendentemente pequeno. A melhoria de Gibbs sobre isso se tornou dramática - embora você ainda precise pensar um pouco sobre isso.

Imagine uma dúzia de recortes de papel de vários tamanhos e formas no chão. Agora imagine que você é oferecido para criar outra forma grande o suficiente para cobrir qualquer uma das formas disponíveis. Através da experimentação - sobrepondo formas e transformando-as - você pode encontrar uma maneira de resolver esse problema. Mas, tendo encontrado uma cobertura universal, você pode ter certeza de que encontrou a menor? Você pode imaginar que, durante o dia, retorne periodicamente ao seu formulário e encontre a oportunidade de cortar peças adicionais aqui e ali.

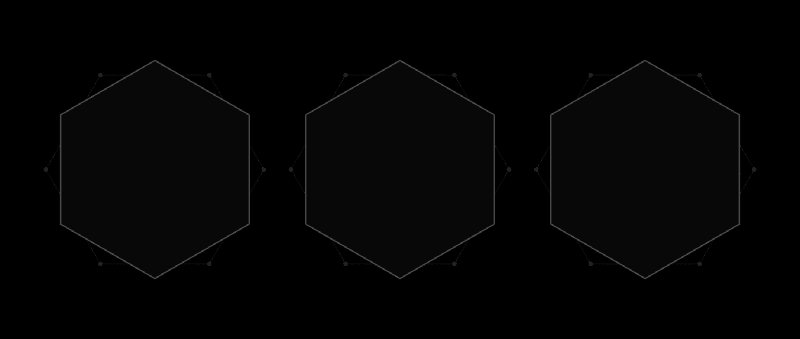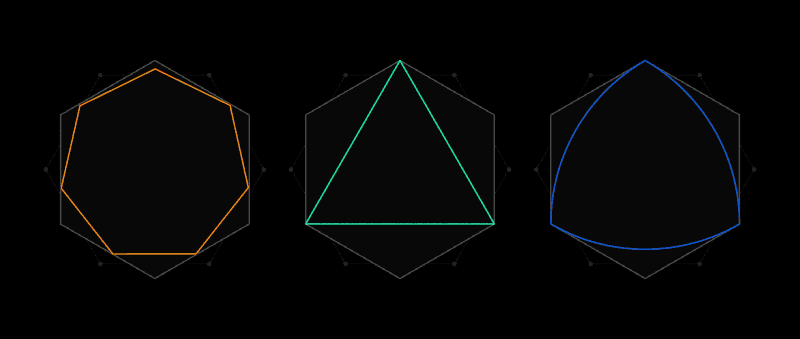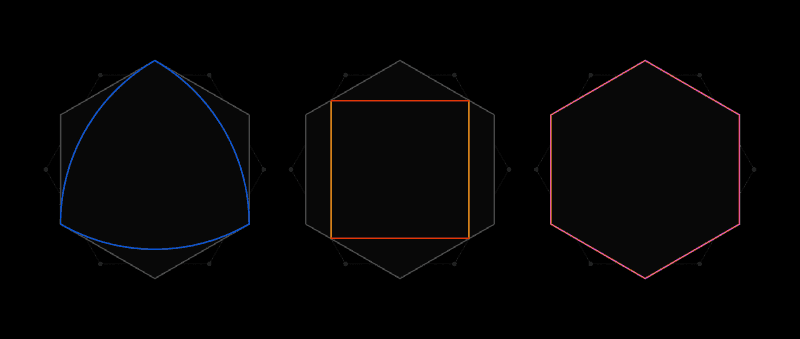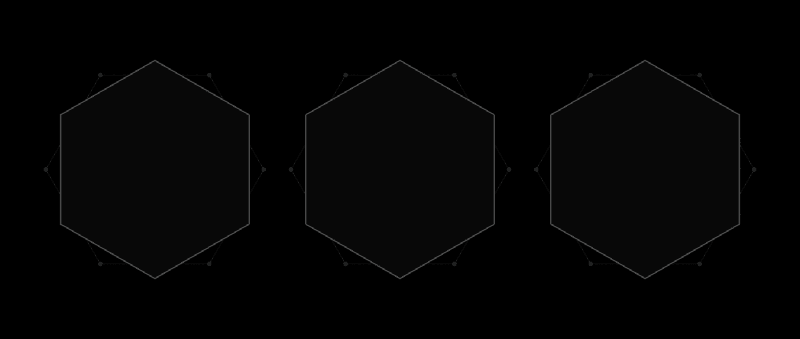
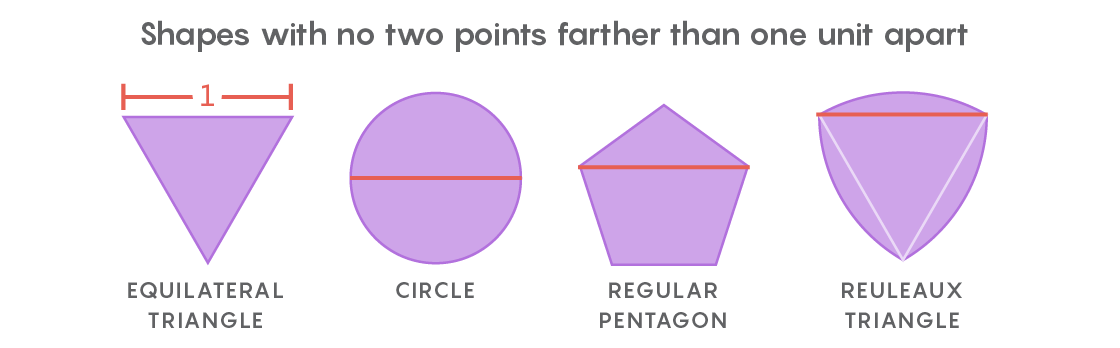
Esse é o espírito do problema de cobertura universal da Lebesgue. Em vez de recortes de papel, considera formas em que dois pontos são espaçados não mais que uma unidade de comprimento. A forma mais óbvia será um círculo de diâmetro 1, mas há um número infinito deles: um triângulo equilátero, um pentágono regular, um hexágono regular, uma forma triangular com lados inchados, conhecida como triângulo de Röhlo - e isso é apenas para iniciantes. A variedade de formas dificulta a menor cobertura de todas.



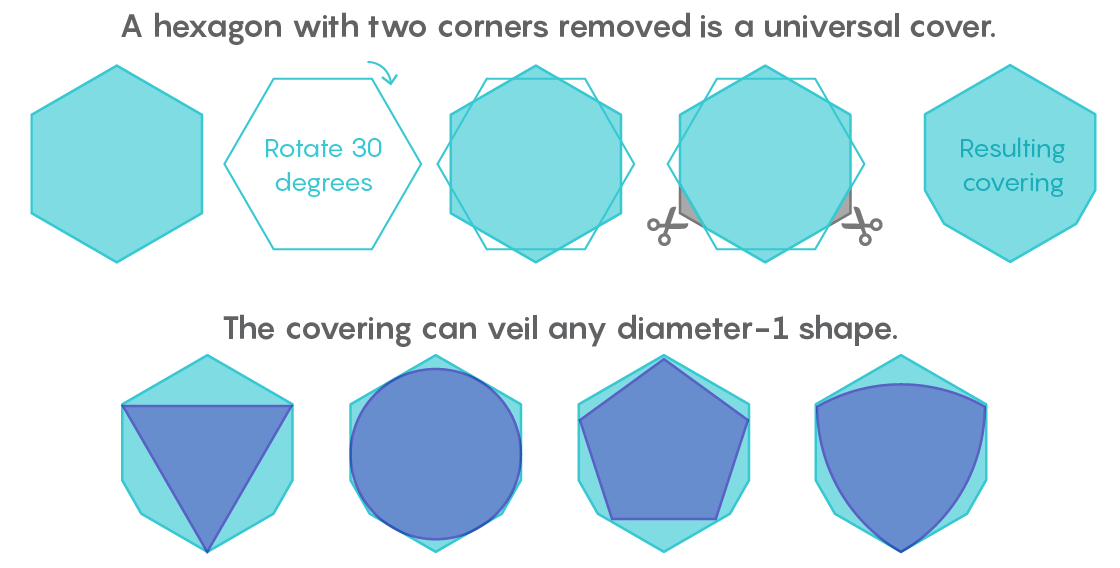
Logo após receber uma carta de Lebesgue, Pal percebeu que o hexágono regular seria a capa universal. E então ele melhorou esse resultado, observando que cortando dois cantos do hexágono, sem ficar um ao lado do outro, você pode obter uma forma com uma área menor, que ainda será um revestimento universal.

“Pegue um hexágono, coloque um segundo em cima, gire 30 graus e corte dois cantos. Foi aí que Pal terminou a pesquisa ", disse Gibbs.

Nos próximos 80 anos, dois outros matemáticos cortaram tiras estreitas da capa universal de Pal. Em 1936, Roland Sprag removeu um pequeno pedaço ao lado de um dos cantos. Em 1992, Hansen removerá duas cunhas em miniatura dos cantos inferiores direito e esquerdo. As ilustrações de Hansen podiam transmitir a localização dessas peças, mas não o tamanho: a área era de 0,00000000004 unidades.



"Você não pode desenhá-los em escala, eles seriam do tamanho de um átomo", disse John Baez , matemático da Universidade da Califórnia em Riverside.

Baez tirou a tarefa de Lebesgue do esquecimento quando escreveu sobre isso em seu blog sobre matemática popular em 2013. Ele admitiu que estava fascinado por essa tarefa de uma maneira que um vídeo com um inseto se afogando poderia fasciná-lo. "Meu interesse pela tarefa não era saudável", escreveu BAez. "Não sei as razões pelas quais isso pode ser importante." Não vejo como ele pode se conectar com muitas outras tarefas maravilhosas. Parece incrivelmente complexo em comparação com a primeira impressão. Admiro as pessoas que trabalham nela tanto quanto admiro as pessoas que decidem atravessar a Antártida em esquis. ”

Philip Gibbs nunca atravessou a Antártida em esquis, mas leu o blog Baez. Quando ele encontrou um registro do problema de Lebesgue, ele pensou: "Bem, é exatamente disso que eu preciso".

Tesoura atômica

Gibbs uma vez pensou que poderia se tornar um cientista. Ele recebeu um diploma em matemática pela Universidade de Cambridge e um doutorado em física teórica pela Universidade de Glasgow. No entanto, ele logo perdeu o entusiasmo pela pesquisa acadêmica e se tornou um programador. Ele trabalhou em sistemas para projeto de navios, gerenciamento de tráfego aéreo e finanças e, em 2006, se aposentou.

Gibbs permaneceu interessado em assuntos acadêmicos, mas como pesquisador leigo ele pouco pôde fazer. "É difícil para um cientista independente acompanhar o que está acontecendo", disse ele. "Mas se você encontrar o nicho certo, poderá fazer alguma coisa e obter alguns resultados úteis."


Matemático amador Philip Gibbs

Tal nicho era o problema de cobertura universal da Lebesgue. Essa tarefa nunca recebeu a atenção de matemáticos, então ele suspeitou que poderia alcançar algum progresso. Gibbs também percebeu que sua experiência em programação poderia ser uma vantagem. "Eu sempre procuro problemas nos quais computadores e matemática experimental possam ser usados", disse ele.

Em 2014, Gibbs executou uma simulação em computador para 200 formas aleatórias de diâmetro 1. A partir das simulações, foi possível que ele pudesse cortar um pequeno pedaço do canto superior da menor capa anterior. Ele transformou isso em prova de que o novo revestimento funcionará para todas as formas possíveis de diâmetro 1. Gibbs enviou a prova a Baez, que, junto com uma de suas alunas, Karina Baghdasaryan, ajudou Gibbs a dar ao trabalho um estilo matemático formal.

Os três publicaram seu trabalho na Internet em fevereiro de 2015. Reduziu a área da menor cobertura universal possível de 0,8441377 para 0,8441153 unidades. A economia de 0,0000224 unidades foi quase um milhão de vezes maior do que a Hansen alcançou em 1992.

Gibbs estava confiante de que poderia melhorar o resultado. Em um trabalho publicado em outubro, ele cortou outro pedaço relativamente grande de um revestimento universal, elevando sua área para 0,84409359 unidades.



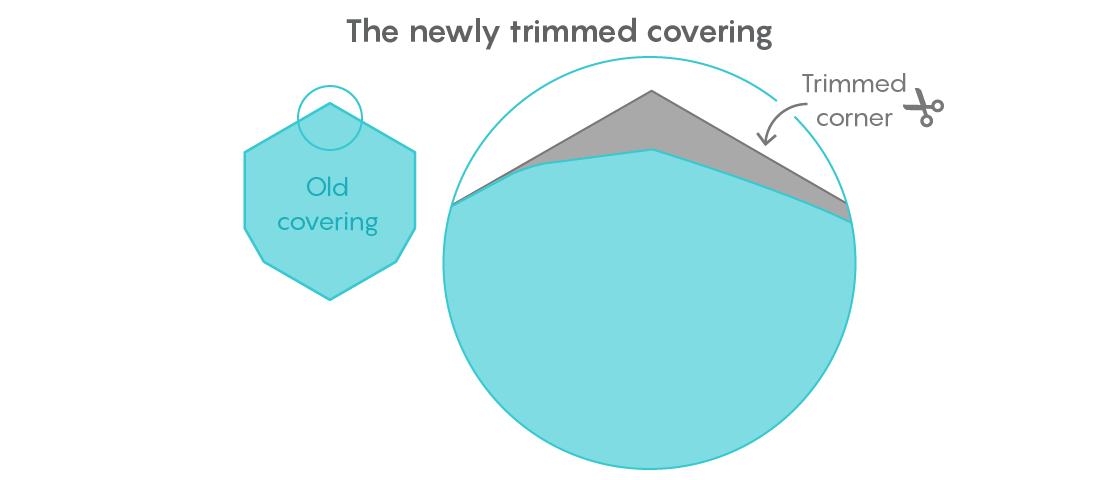
Sua estratégia era mover todas as formas com um diâmetro de 1 para o canto do revestimento universal que ele descobriu há vários anos e depois remover toda a área restante do canto oposto. Mas uma medição precisa do espaço economizado se mostrou difícil. As técnicas usadas por Gibbs foram baseadas na geometria euclidiana, mas foram realizadas com tanta precisão que chocaria qualquer estudante do ensino médio.

“Do ponto de vista da matemática, tudo isso é geometria para o ensino médio. Mas tocou com tensão fanática ” , escreveu Baez.

Até agora, Gibbs ocupa o primeiro lugar em busca da menor cobertura universal, mas seu prêmio está em perigo. Gibbs acredita que há uma oportunidade de encontrar uma cobertura ainda menor. Baez espera que a atenção que Gibbs retornou ao problema de Lebesgue estimule o interesse de outros matemáticos. Talvez seja hora de deixar de lado o governante e a bússola e usar todo o arsenal da matemática moderna.

"É possível que a maneira correta de resolver esse enigma use idéias completamente diferentes", disse ele, "embora eu não tenha idéia de quais idéias possam ser essas".