Precisão de profundidade claramente

A precisão da profundidade é um problema que qualquer programador gráfico enfrentará mais cedo ou mais tarde. Muitos artigos e trabalhos foram escritos sobre esse assunto. E em diferentes jogos e mecanismos, e em diferentes plataformas, você pode ver muitos formatos e configurações diferentes para o buffer de profundidade .

A conversão de profundidade em uma GPU parece não óbvia por causa de como ela interage com a projeção em perspectiva, e o estudo das equações não esclarece a situação. Para entender como isso funciona, é útil desenhar algumas figuras.



Este artigo está dividido em 3 partes:

1. Vou tentar explicar a motivação para a transformação de profundidade não linear .
2. Apresentarei vários gráficos que ajudarão você a entender como a conversão de profundidade não linear funciona em diferentes situações, intuitiva e visualmente.
3. Uma discussão das principais descobertas de Apertando a precisão da renderização em perspectiva [Paul Upchurch, Mathieu Desbrun (2012)] sobre o efeito dos erros de ponto flutuante na precisão da profundidade.

Por que 1 / z?

Um buffer de profundidade da GPU de hardware geralmente não armazena uma representação linear da distância entre o objeto e a câmera, ao contrário do que é ingenuamente esperado dele na primeira reunião. Em vez disso, o buffer de profundidade armazena valores inversamente proporcionais à profundidade do espaço de visualização. Quero descrever brevemente a motivação para essa decisão.

Neste artigo, usarei d para representar os valores armazenados no buffer de profundidade (no intervalo [0, 1] para DirectX) e z para representar o espaço de visualização em profundidade, ou seja, A distância real da câmera, em unidades mundiais, por exemplo, metros. Em geral, o relacionamento entre eles tem a seguinte forma:



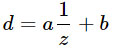
onde a, b são as constantes associadas às configurações de perto e de longe dos planos. Em outras palavras, d é sempre alguma transformação linear de 1 / z .

À primeira vista, pode parecer que qualquer função de z possa ser tomada como d . Então, por que ela parece assim? Existem duas razões principais para isso.

Em primeiro lugar, 1 / z se encaixa naturalmente na projeção em perspectiva. E esta é a classe mais básica de transformações, garantida para preservar linhas. Portanto, a projeção em perspectiva é adequada para rasterização de hardware, pois as bordas retas dos triângulos permanecem retas na tela. Podemos obter uma transformação linear a partir de 1 / z , aproveitando a divisão de perspectiva que a GPU já realiza:



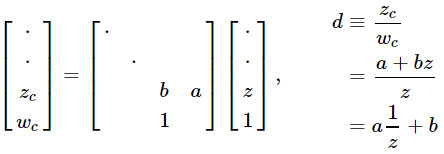
Obviamente, a força real dessa abordagem é que a matriz de projeção pode ser multiplicada por outras matrizes, permitindo combinar muitas transformações em uma.

A segunda razão é que 1 / z é linear no espaço da tela, como observou Emil Persson . Isso facilita a interpolação de d no triângulo durante a rasterização, e coisas como buffers Z hierárquicos , buffer de profundidade de compactação e seleção antecipada de Z.

Gráficos de profundidade

As equações são complicadas, vamos ver algumas fotos!



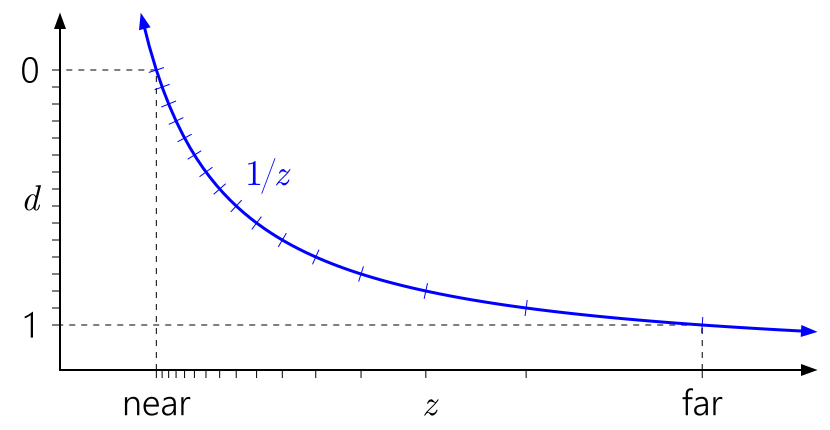
A maneira de ler esses gráficos é da esquerda para a direita e depois para baixo. Comece com d no eixo esquerdo. Como d pode ser uma transformação linear arbitrária de 1 / z , podemos organizar 0 e 1 em qualquer local conveniente no eixo. Marcas indicam diferentes valores de buffer de profundidade . Para fins de clareza, modelo um buffer de profundidade normalizado inteiro de 4 bits, para que haja 16 marcas espaçadas igualmente.

O gráfico acima mostra a conversão de profundidade de baunilha "padrão" para D3D e APIs semelhantes. Você pode perceber imediatamente como, devido à curva 1 / z , os valores próximos ao plano próximo são agrupados e os valores próximos ao plano distante estão dispersos.

Também é fácil entender por que perto de um avião afeta tanto a precisão da profundidade. A distância perto do plano levará a um rápido aumento nos valores de d em relação aos valores de z , o que levará a uma distribuição ainda mais desigual de valores:



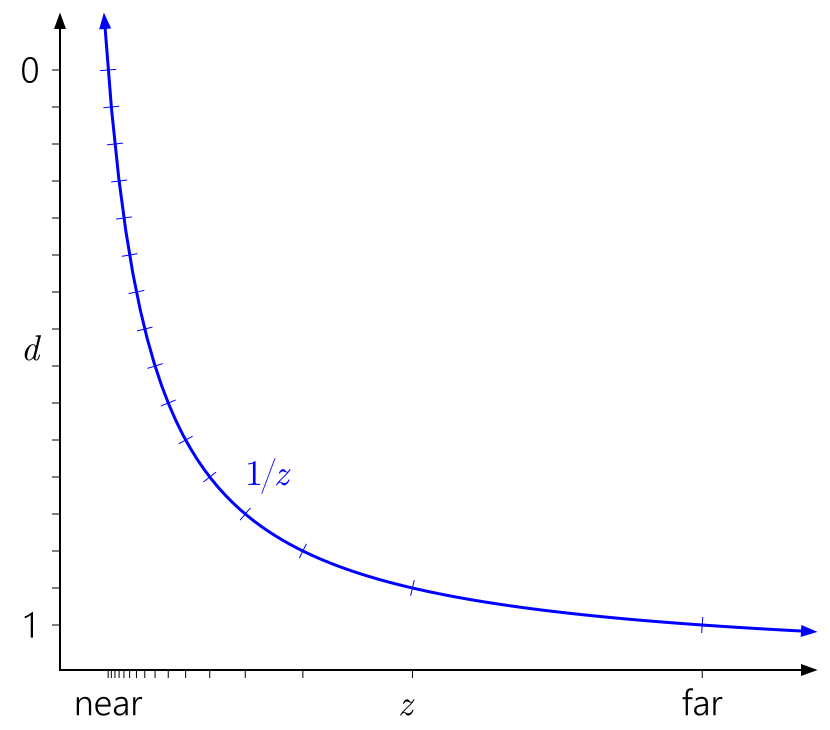
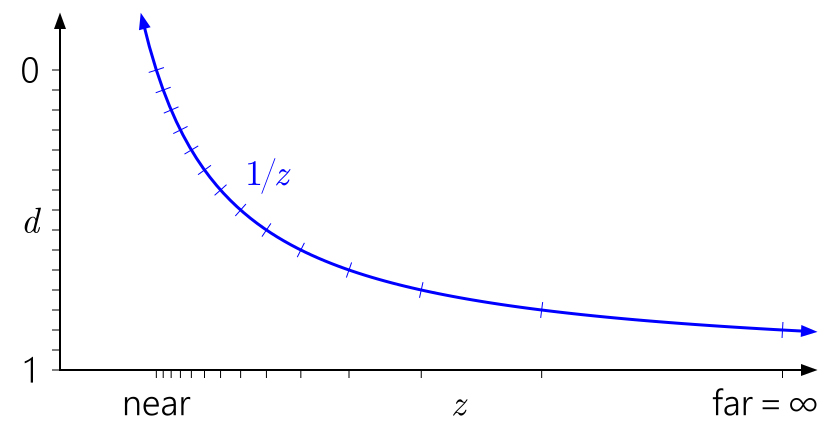
Da mesma forma, neste contexto, é fácil ver por que mover o plano distante para o infinito não tem um efeito tão grande. Significa apenas expandir o intervalo de d para 1 / z = 0 :



Mas e a profundidade de ponto flutuante? O gráfico a seguir foi adicionado às marcas correspondentes ao formato flutuante com 3 bits do expoente e 3 bits da mantissa:



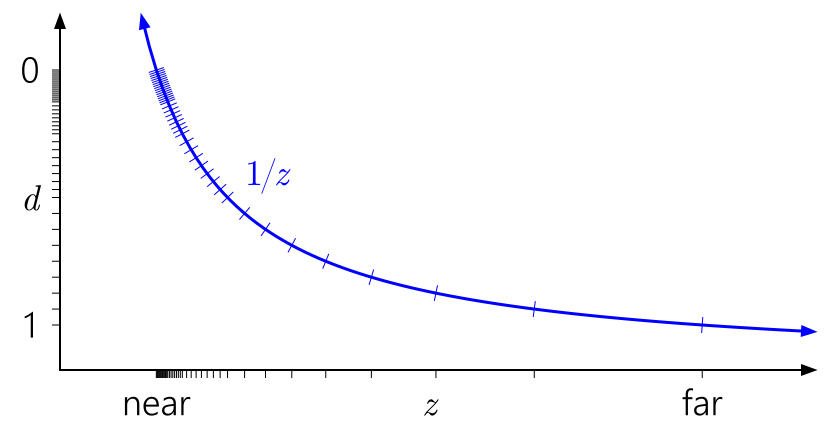
Agora, no intervalo [0,1], existem 40 valores diferentes - um pouco mais de 16 valores anteriores, mas a maioria deles é agrupada inutilmente perto do plano próximo (mais próximo de 0 o flutuador tem maior precisão), onde realmente não precisamos de muita precisão.

Agora, um truque conhecido é inverter a profundidade, exibindo o plano próximo em d = 1 e o plano distante em d = 0 :



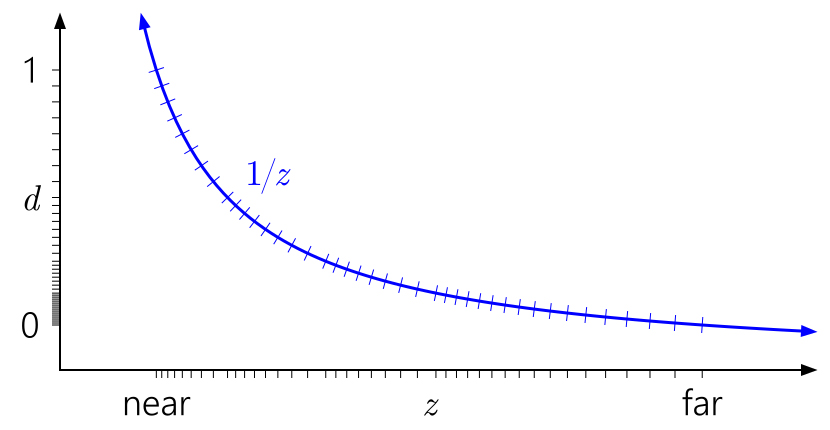
Muito melhor! Agora, a distribuição quase-logarítmica do flutuador de alguma forma compensa a não linearidade de 1 / z , enquanto mais próximo do plano próximo ele fornece uma precisão semelhante ao buffer de profundidade inteira e fornece uma precisão significativamente maior em outros lugares. A precisão da profundidade se deteriora muito lentamente se você se afastar da câmera.

O truque do Z reverso pode ter sido reinventado de forma independente várias vezes, mas pelo menos a primeira menção foi no artigo SIGGRAPH '99 [Eugene Lapidous e Guofang Jiao (infelizmente não está disponível ao público)]. E, recentemente, ele foi mencionado novamente no blog por Matt Petineo e Brano Kemen , e em um discurso de Emil Persson Criando Vast Game Worlds SIGGRAPH 2012.

Todos os gráficos anteriores assumiram uma faixa de profundidade [0,1] após a projeção, o que é uma convenção no D3D. E o OpenGL ?



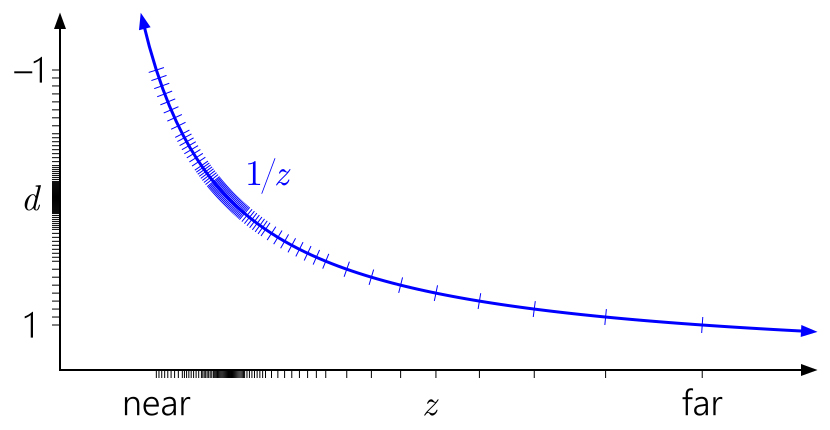O OpenGL, por padrão, assume uma faixa de profundidade [-1, 1] após a projeção. Para formatos inteiros, nada muda, mas para ponto flutuante, toda a precisão está concentrada inútil no meio. (O valor da profundidade é mapeado para o intervalo [0,1] para armazenamento subseqüente no buffer de profundidade, mas isso não ajuda, pois o mapeamento inicial para [-1,1] já destruiu toda a precisão na metade mais distante do intervalo.) E, devido à simetria, o truque Z reverso não funcionará aqui.

Felizmente, na área de trabalho OpenGL, isso pode ser corrigido usando a extensão amplamente suportada ARB_clip_control (também começando com o OpenGL 4.5, glClipControl é padrão ). Infelizmente, o GL ES está em voo.

O efeito de erros de arredondamento

A conversão 1 / z e a escolha do buffer de profundidade float x int são uma grande parte da história da precisão, mas não todas. Mesmo se você tiver precisão de profundidade suficiente para representar a cena que está tentando renderizar, é fácil degradar a precisão com erros aritméticos durante o processo de conversão de vértices.

No início do artigo, foi mencionado que Upchurch e Desbrun estudaram esse problema. Eles propuseram duas recomendações principais para minimizar os erros de arredondamento:

1. Use plano distante infinito.
2. Mantenha a matriz de projeção separada de outras matrizes e aplique-a como uma operação separada no shader de vértice, em vez de combiná-la com a matriz de vista.

Upchurch e Desbrun fizeram essas recomendações usando um método analítico baseado no processamento de erros de arredondamento como pequenos erros aleatórios representados em cada operação aritmética e rastreando-os até a primeira ordem no processo de conversão. Eu decidi testar os resultados na prática.

As fontes aqui são Python 3.4 e numpy. O programa funciona da seguinte maneira: uma sequência de pontos aleatórios é gerada, ordenada por profundidade, localizada linear ou logaritmicamente entre planos próximos e distantes. Em seguida, os pontos são multiplicados pelas matrizes de vista e projeção e a divisão de perspectiva é realizada, usando flutuadores de 32 bits e, opcionalmente, o resultado final é convertido em um int de 24 bits. No final, ele passa pela sequência e conta quantas vezes dois pontos vizinhos (que inicialmente tinham profundidades diferentes) se tornaram idênticos, porque tinham a mesma profundidade ou a ordem foi alterada. Em outras palavras, o programa mede a frequência com que erros de comparação de profundidade ocorrem - o que corresponde a problemas como o Z-fighting - em vários cenários.

Aqui estão os resultados para near = 0.1, far = 10K, com uma profundidade linear de 10K. (Tentei o intervalo de profundidade logarítmico e outras razões perto / longe e, embora os números específicos variassem, as tendências gerais nos resultados eram as mesmas.)

Na tabela, “eq” - dois pontos com a profundidade mais próxima obtêm o mesmo valor no buffer de profundidade e “swap” - dois pontos com a profundidade mais próxima são trocados.

	Matriz composta de vista e projeção		Matrizes separadas de vista e projeção
	float32	int24	float32	int24
Valores Z inalterados (teste de controle)	0% eq Troca de 0%	0% eq Troca de 0%	0% eq Troca de 0%	0% eq Troca de 0%
Projeção padrão	45% eq Swap de 18%	45% eq Swap de 18%	77% eq Troca de 0%	77% eq Troca de 0%
Infinito longe	45% eq Swap de 18%	45% eq Swap de 18%	76% eq Troca de 0%	76% eq Troca de 0%
Z invertido	0% eq Troca de 0%	76% eq Troca de 0%	0% eq Troca de 0%	76% eq Troca de 0%
Infinito + Z reverso	0% eq Troca de 0%	76% eq Troca de 0%	0% eq Troca de 0%	76% eq Troca de 0%
Padrão + estilo GL	56% eq Swap de 12%	56% eq Swap de 12%	77% eq Troca de 0%	77% eq Troca de 0%
Infinito + estilo GL	59% eq Swap de 10%	59% eq Swap de 10%	77% eq Troca de 0%	77% eq Troca de 0%

Peço desculpas pelo fato de que, sem um gráfico, há muita dimensão aqui e simplesmente não é possível construí-lo! De qualquer forma, olhando os números, as seguintes conclusões são óbvias:

• Na maioria dos casos, não há diferença entre o buffer int e float depth . Erros aritméticos para calcular erros de substituição de profundidade na conversão para int. Em parte porque float32 e int24 têm ULP quase igual (a unidade de menor precisão é a distância do número vizinho mais próximo) por [0.5.1] (como o float32 tem uma mantissa de 23 bits), portanto, um erro de conversão não é adicionado em quase toda a faixa de profundidade em int.
• Na maioria dos casos, a separação das matrizes de visão e projeção (seguindo as recomendações de Upchurch e Desbrun) melhora o resultado. Apesar do fato de a taxa de erro geral não diminuir, os “swaps” se tornam valores iguais, e este é um passo na direção certa.
• O plano infinito distante altera ligeiramente a frequência dos erros. Upchurch e Desbrun previram uma redução de 25% na frequência de erros numéricos (erros de precisão), mas isso não parece levar a uma diminuição na frequência de erros de comparação.

No entanto, as descobertas acima não são reais em comparação com o Z reverso mágico. Verifique:

• O Z reverso com buffer de profundidade de flutuação fornece uma taxa de erro zero no teste. Agora, é claro, você pode obter alguns erros se continuar aumentando o intervalo dos valores de profundidade de entrada. No entanto, o Z reverso com flutuação é ridiculamente mais preciso do que qualquer outra opção.
• O Z reverso com buffer de profundidade inteira é tão bom quanto outras opções inteiras.
• O Z reverso desfoca a distinção entre matrizes de visão / projeção compostas e separadas e planos distantes finitos e infinitos. Em outras palavras, com Z reverso, você pode multiplicar a projeção com outras matrizes e usar qualquer plano distante que desejar, sem comprometer a precisão.

Conclusão

Eu acho que a conclusão é clara. Em qualquer situação, ao lidar com projeção em perspectiva, basta usar o buffer de profundidade de flutuação e o Z invertido ! E se você não conseguir usar o buffer de profundidade de flutuação, ainda deve usar Z reverso. Isso não é uma panacéia para todos os males, especialmente se você criar um ambiente de mundo aberto com faixas de profundidade extremas. Mas este é um ótimo começo.