
Olá Habr! Meu nome é Akhmadeev Rinat, sou Sr. Desenvolvedor PHP.
Apresento a você o resumo do relatório Torne as senhas ótimas novamente! Como derrotar o bruteforce e deixar hackers com nada de Alexey Ermishkin da Virgil Security com HighLoad ++ 2018 .
Quando fui ao relatório, fiquei pessimista. Mas desde Por ser a Virgil Security, eu ainda decidi ir. No começo, o relatório parecia realmente o do capitão, e eu até comecei a perder o interesse, mas então, como se viu, descobri várias novas abordagens de proteção por senha, além do uso comum de sal.
O relatório discute maneiras de proteger senhas de hashes para abordagens mais modernas, como a senha do Facebook Onion, Sphinx e Pythia. No final, os novos serviços simples de criptografia protegida por senha (PHE) são introduzidos.
Gostei tanto do relatório que preparei um compêndio. Eu recomendo a todos que se familiarizem.
Alexey Ermishkin compartilhou os slides e a reportagem em vídeo nos comentários:
Resumo
Entrada

Olá pessoal, bom dia pessoal! Fico feliz em ver todos vocês na Conferência Highload. Meu nome é Alexey Ermishkin, trabalho para a Virgil Security.

Estamos envolvidos no desenvolvimento de vários produtos criptográficos, tanto para desenvolvedores individuais quanto para empresas. Nós nos concentramos em soluções de ponta a ponta, é quando você não precisa confiar no serviço para executar ações como transferência de dados, autenticação, etc. Nossos SDKs são abertos e acessíveis a todos.
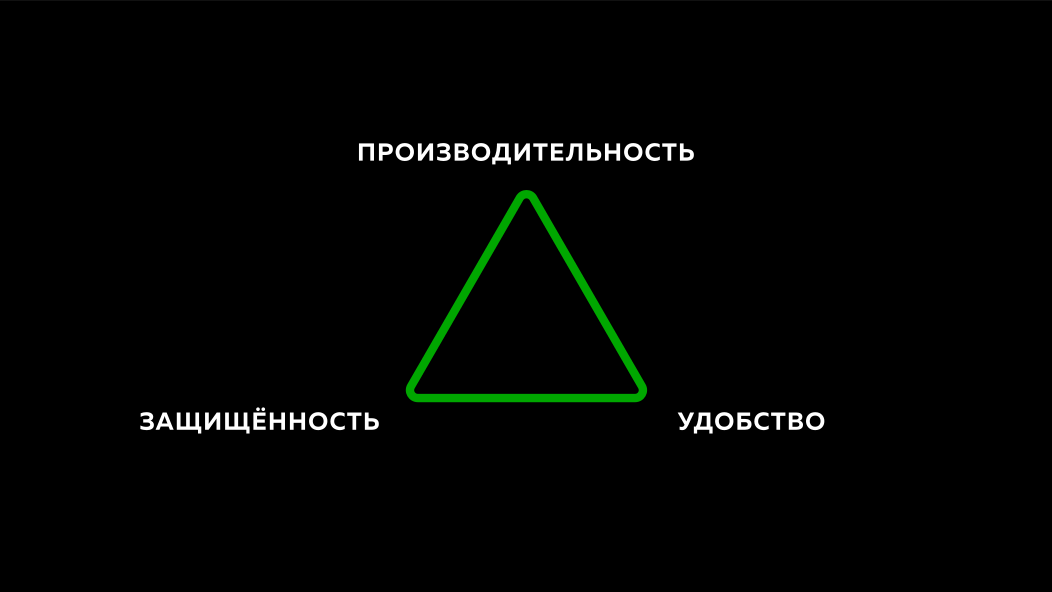
As senhas são usadas há muito tempo como meio de autenticação, como forma de chegar a algum lugar. Isso foi muito antes dos computadores aparecerem. Mas com o advento dos computadores, com o advento dos sistemas de TI, as pessoas não abandonaram o hábito de usar senhas. Isso se tornou um grande problema para os desenvolvedores, porque eles enfrentaram o problema de como tornar os sistemas convenientes, rápidos e seguros. Muitas vezes, quando alguns desses aspectos estão tentando se sair bem, o terceiro não funciona muito bem. Se você tornar o sistema produtivo e seguro, poderá ser inconveniente, etc.

Então, sobre o que vamos falar hoje?
Vou falar sobre proteção contra ataques offline. Quando as senhas entram nos seus bancos de dados, o usuário não as controla. Se o seu banco de dados for invadido, ele vazará em algum lugar e, depois disso, os hackers poderão fazer qualquer coisa com ele. Mesmo que você tenha protegido as senhas, elas podem começar a separá-las e não precisam interagir com ninguém para isso, elas já têm tudo para isso. Além disso, os usuários não param de usar senhas fracas. As políticas de senha são obviamente úteis, mas também nem sempre são convenientes, ou seja, quando até as pessoas digitam parecer uma senha forte, a política ainda diz que você precisa adicionar uma letra ou um número; então, para elas, não é conveniente. Também é óbvio que o problema é a necessidade de comparar o que o usuário digitou com o que você possui no banco de dados. Como fazer isso de maneira segura? Bem, não vamos esquecer que, dentro da empresa, também existem pessoas que não são completamente amigáveis e gostariam de se proteger delas também.
Hashes
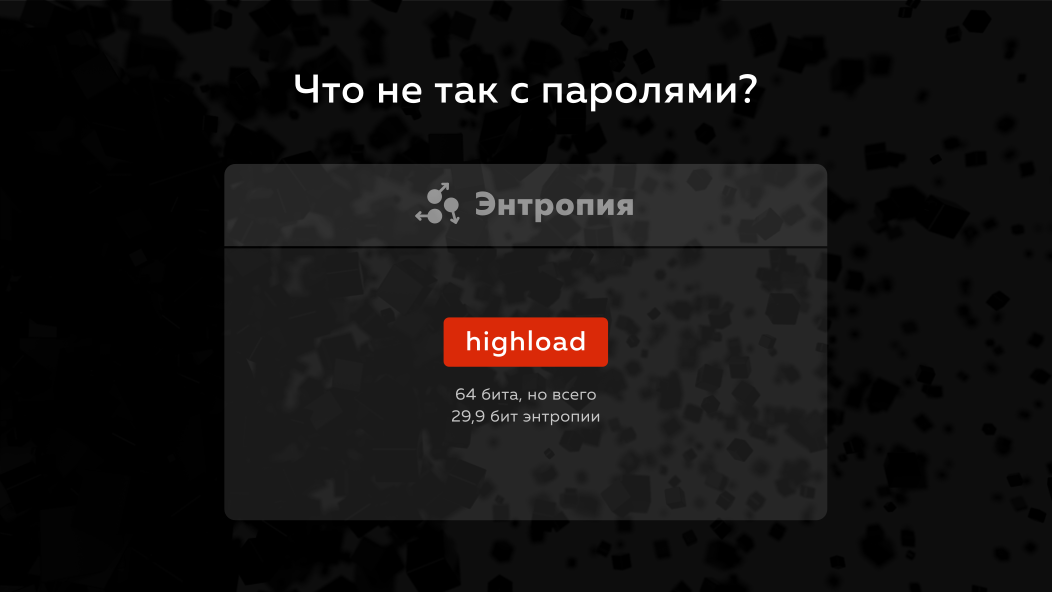
Em princípio, por que as senhas são um assunto tão dolorido, por que vale a pena trabalhar com elas com mais cuidado? O problema é que a senha tem uma pequena entropia . O que é entropia? Essa é a quantidade de informações contidas nos dados, ou seja, por exemplo, na palavra Highload, 8 letras são 8 bytes, mas se contarmos a entropia, ela não terá 64 bits como a palavra inteira, mas menos de 30 bits. Hoje, quando eles falam sobre quebrar a senha, dizem que é possível decifrar senhas com entropia em um tempo que não existe mais ou menos que tantos bits. I.e. mesmo o número exato de senhas não é levado em consideração.

Como as pessoas começaram a usar a segurança de senhas? A primeira coisa que veio à mente foi usar hashes criptográficos unidirecionais.

Sua característica notável é que eles não podem ser devolvidos. I.e. Se você transferiu algumas informações para esse hash, recebeu um valor na saída, não será possível recuperar essas informações a partir desse valor. Mas, infelizmente, eles são calculados muito rapidamente. Por exemplo, um cluster moderno de 4 placas gráficas NVidia pode processar vários bilhões de senhas por segundo. I.e. se a entropia da sua senha for inferior a 40 bits, um cluster de 4 placas de vídeo a buscará em um minuto ou até menos.
Mesas de arco-íris

Além disso, cada hash complicado tem sua própria tabela de arco-íris . O que é esta tabela e como eles são feitos?

I.e. eles pegam as senhas mais populares e as combinações de caracteres que podem caber no disco rígido, consideram hashes para eles e os colocam em um pouco mais de armazenamento por vários terabytes. Quando existe algum tipo de hash, não é possível calculá-lo, mas encontre-o muito rapidamente nessas tabelas e compare-o com a senha que foi calculada anteriormente. I.e. As vantagens das tabelas são que elas funcionam muito rapidamente, mas você precisa de muito espaço para armazená-las. No entanto, existem tabelas para os hashes mais populares da Internet, que podem ser baixados ou comprados.
Nota do autor da sinopse: A Wikipedia não concorda com o falante: "A tabela Rainbow é uma versão especial das tabelas de pesquisa para reverter funções hash criptográficas usando o mecanismo de um compromisso razoável entre o tempo de pesquisa na tabela e a memória ocupada". I.e. ele não armazena os hashes das senhas mais populares que cabem no disco, mas simplesmente os hashes de algumas senhas; o restante é calculado com base nas que existem - existem várias senhas por registro na tabela.
Sal

Mas, novamente, cada mesa arco-íris tem seu próprio sal . O que é sal? Este é um conjunto aleatório de bytes, que é anexado à senha. Ele é armazenado em uma tabela em algum lugar próximo ao hash e protege das tabelas do arco-íris.

I.e. as pessoas que colocam as mãos em uma base com hashes salgados ainda precisam calcular esses hashes. Mas o problema é que esses hashes são calculados muito rapidamente e o sal não ajuda muito aqui.
Como retardar a pesquisa?

Uma saída natural disso poderia ser retardar a classificação de hash de alguma maneira. Como isso pode ser feito?

A abordagem mais ingênua é que pegamos algum tipo de função hash, por exemplo sha256, e a computamos iterativamente, ou seja, calcular o hash, a partir deste hash o hash novamente, etc. Você pode fazer isso milhares e até milhões de vezes. O problema é que, se você escrever uma implementação desse tipo, provavelmente será mais lenta que a implementação de pessoas envolvidas profissionalmente na adivinhação de senha.

SCrypt , Bcrypt , Argônio2
E, portanto, os criptografadores criaram várias funções projetadas especificamente para retardar a pesquisa de senhas - eles usam uma grande quantidade de memória e todas as instruções modernas possíveis do processador. Se a senha protegida por essa função cair nas mãos dos atacantes, eles terão que usar um hardware muito poderoso.

Por exemplo, a função Argon2 mais moderna funciona da seguinte maneira: no diagrama, você pode ver que existem muitos blocos de memória diferentes através dos quais o hash é executado. Ele faz isso de várias maneiras, ida e volta, a memória é usada com muita intensidade, toda a memória é usada. É bastante difícil otimizar essa função (velocidade de pesquisa).

Mas essas abordagens também têm suas desvantagens. Essas funções são lentas especialmente, mas são lentas não apenas para os atacantes, mas também são lentas para você. Eles vão carregar seu ferro. Essas funções são personalizáveis, ou seja, você pode escolher quanta memória será usada para calcular o hash de uma única senha, até vários gigabytes, quantas passagens nessa memória. Se você enrolar esses parâmetros com muita seriedade, seu próprio hardware sofrerá e se houver muitas pessoas conectando-se ao sistema, basta alocar recursos substanciais para a proteção de senhas e senhas simples. Bem, senhas muito simples ainda podem ser obtidas .
Senha do Facebook Onion

As pessoas pensaram sobre isso e fizeram a pergunta: é possível obter as mesmas propriedades sem carregar o back-end, sem carregar seus próprios servidores?

Um dos pioneiros nisso foi o Facebook . Essas linhas que você vê são os estágios históricos do Facebook, como eles protegiam senhas, no início eram apenas senhas, depois pegaram a antiga função md5 , que foi quebrada por um longo tempo, depois adicionaram sal lá e pegaram o hash sha1 , e aconteceu interessante, eles trouxeram o cálculo da função hmac (este é um hash com uma chave) para o serviço remoto.
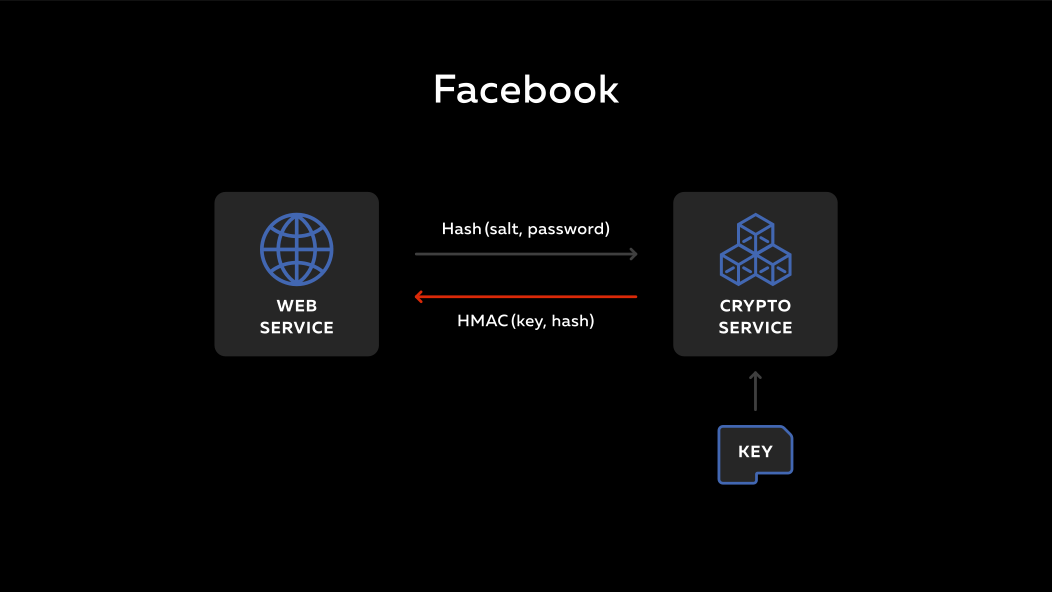
Como isso funciona? Há um back-end, há um serviço remoto. Existe algum tipo de chave secreta nesse serviço. Uma pessoa entra no back-end, digita sua senha. Essa senha é misturada com o salt que está no banco de dados, é executada através de um hash e enviada ao serviço. O serviço pega sua chave privada, calcula a função hmac e envia tudo de volta. No back-end, é colocado na base.
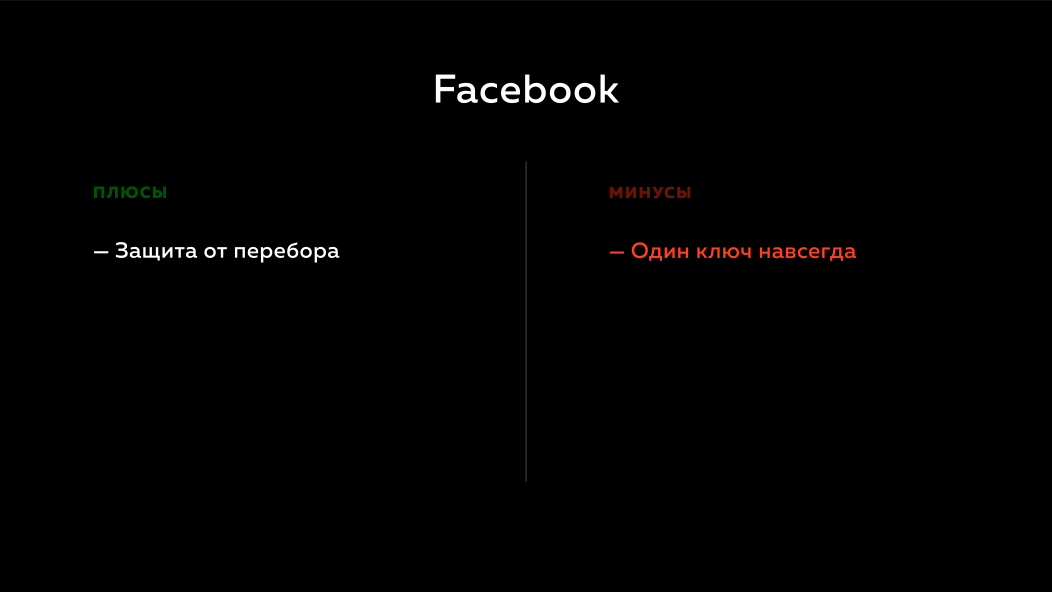
O que isso dá? Se o Facebook tiver um banco de dados de usuários, não vale a pena classificar senhas, porque eles não possuem uma chave secreta remota. Mas o problema com a abordagem do Facebook é que, se algo acontecer com sua chave privada remota, eles terão grandes problemas. Eles não podem fazer nada porque usam hashes, eles usam hmac. Eles não têm como resolver de alguma forma essa situação, para que os usuários não notem nada, e isso acaba levando a um canto.
Esfinge
Os criptografadores olharam para a coisa toda. Eles gostaram da ideia de usar serviços remotos e decidiram pensar: é possível fazer ainda melhor? É possível criar um sistema semelhante, mas sem os inconvenientes que o Facebook o dotou?

E eles decidiram abordar esse problema da seguinte maneira: e se a senha ou o hash da senha for representado como um número? Se temos a palavra passw0rd , ela consiste em 8 bytes. Em quase todas as linguagens de programação, existem tipos inteiros de oito bytes, ou seja, Em princípio, este é o mesmo. I.e. 8 bytes, a palavra passw0rd e podemos representá-la como um número decimal regular. O que isso nos dá? Isso nos dá uma liberdade de ação completamente diferente. Podemos adicionar senhas ou hashes a partir deles, multiplicá-los, transformá-los em outros números. Podemos realizar operações matemáticas realmente sérias com eles.

Um dos primeiros sistemas que usaram essa tecnologia foi o Sphinx . Ela apareceu alguns anos atrás. Este é um gerenciador de senhas determinístico. Existem muitos programas diferentes, como o keepass , onde você tem uma senha mestra e, para cada site, gera uma senha aleatória. Mas também existem coisas determinísticas nas quais você digita sua senha mestra, o site que deseja acessar e calcula algo lá e emite uma senha exclusiva para cada site. Mas é claro que, se essa senha mestre for para algum lugar, todas as senhas dos seus sites serão permanentemente comprometidas.
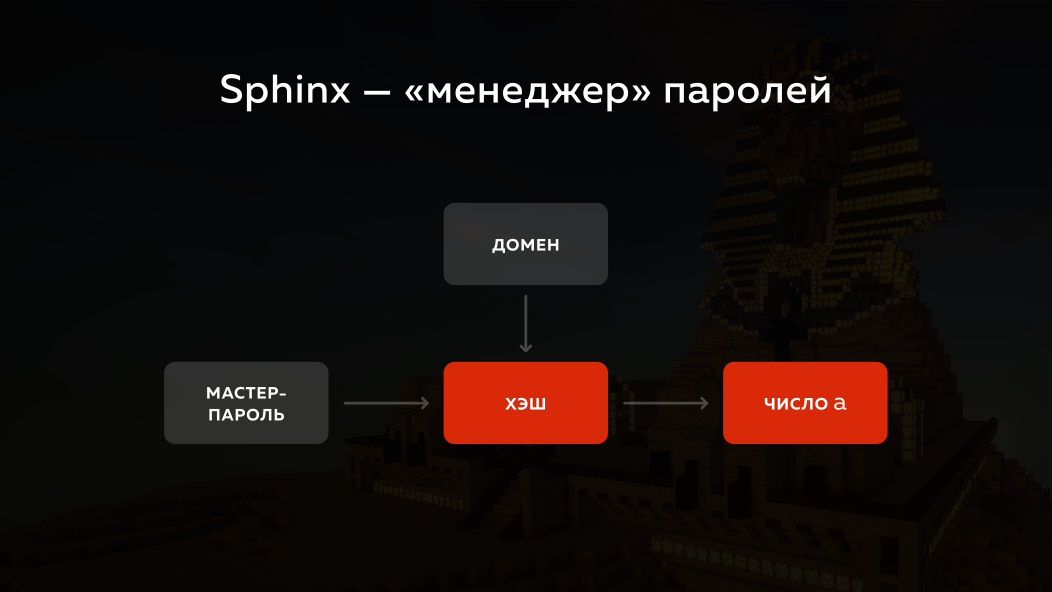
Como a Sphinx abordou esse problema? Ele pega a senha mestra, pega o domínio no qual você deseja fazer login, executa a coisa toda através de um hash e a transforma em número. Mas, de fato, a criptografia elíptica é usada lá, para simplificar explicarei tudo isso em números comuns com a matemática comum. Ele o transforma em um número (vamos chamá-lo de) e o que ele faz a seguir?

Coisa absolutamente maravilhosa, toda vez que podemos gerar um grande número aleatório r . Se elevarmos o número a à potência de r , e algum tempo depois elevarmos esse número à potência inversa ao número r , voltaremos ao mesmo número a , certo? I.e. podemos mascarar algo desde o começo e depois desmascará-lo.
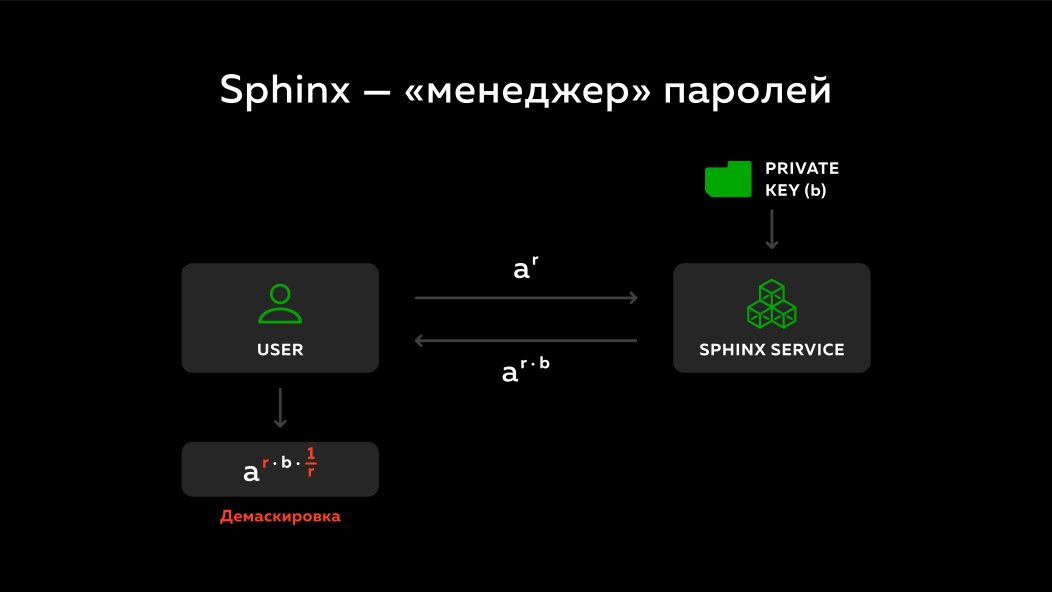
E o que a esfinge faz? Novamente, há um usuário, há um serviço remoto. Um número mascarado é enviado para este serviço remoto. No serviço remoto, há uma chave privada b . O que ele esta fazendo? Ele multiplica o número enviado a^r por sua chave secreta b envia de volta. ( Nota do autor do compêndio: no slide, o número enviado não é multiplicado pela chave privada, mas é aumentado para o grau da chave privada, mas o ponto principal é ). Como o número r diferente a cada vez, o serviço remoto não pode dizer nada sobre qual senha e domínio foram mascarados, ou seja, toda vez que ele vê alguns números aleatórios diferentes. E ele simplesmente multiplica pela sua chave privada b envia de volta.
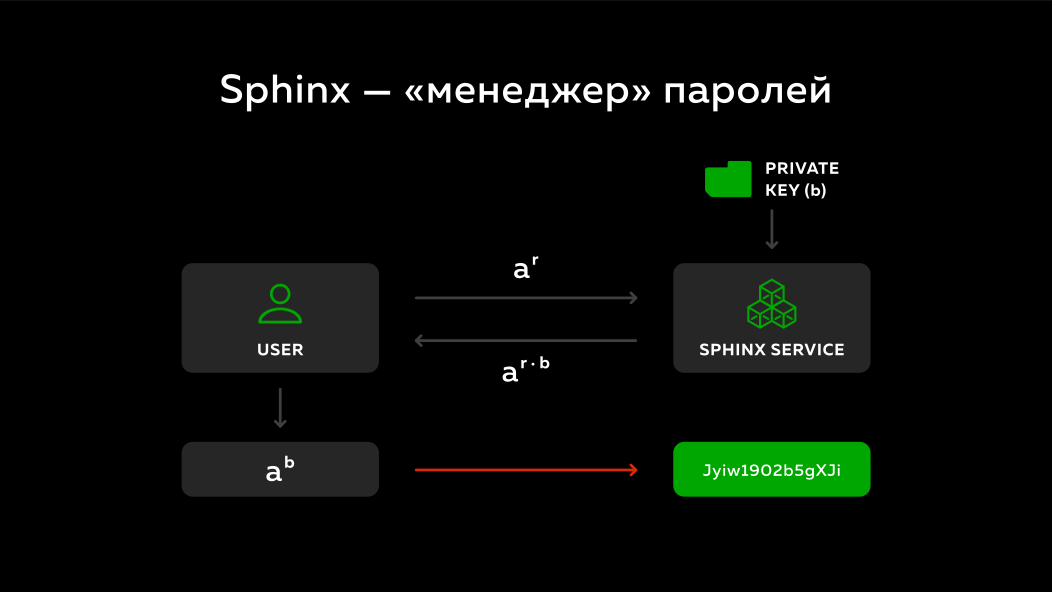
O usuário desmascara o que o servidor enviou e ele recebe um número - sua senha mestre com o domínio multiplicado pela chave secreta do servidor a^b . Acontece que ele não conhece a chave secreta do servidor, o servidor não sabe o que o usuário enviou, mas no final ele também recebe algum tipo de número determinístico. Cada vez que você executa esse protocolo, o disfarce será diferente, mas o resultado será sempre o mesmo e poderá ser transformado em algum tipo de senha e usado para entrar em vários sites.

Tecnologia verdadeiramente maravilhosa. Primeiro, você pode gerar senhas grandes, ou seja, protege de rebentar. Em segundo lugar, se um hacker obtiver acesso a várias senhas, ele não poderá dizer nada sobre o resto, porque eles são gerados independentemente um do outro. Terceiro, se a senha do usuário desaparecer em algum lugar, isso também não dará nada, porque os hackers não terão uma chave secreta. Quarto, funciona muito rapidamente, porque aqui não são necessários hashes grandes iterativos, ou seja, literalmente 2-3 multiplicações são realizadas e tudo funciona instantaneamente.
Mas este sistema tem suas desvantagens. O servidor com o qual o usuário está falando não sabe nada sobre ele. Ele simplesmente recebe alguns números aleatórios como entrada, multiplica-os por algo e os envia de volta. O cliente também não sabe nada sobre o servidor, envia algo para algum lugar, recebe o resultado, funciona - bem. Mas se algo acontecer com o serviço, o usuário não poderá dizer nada sobre ele, ele não terá informações para isso. A chave secreta também não pode ser alterada; nada pode ser feito com ela.
Pythia

Poderia ser melhor?

Os criptografadores examinaram este sistema e pensaram: é possível melhorar o sistema e complementá-lo com propriedades que nos permitiriam dizer que ele cumpre os princípios de ponta a ponta? I.e. o cliente pode se comunicar com o servidor, mas, ao mesmo tempo, também pode autenticá-lo e, em certa medida, confiar nele.

E eles criaram um protocolo chamado Pythia .

Foi feita pelo homem maravilhoso Adam Everspaugh com seus colegas. O que o torna único? Em primeiro lugar, o serviço sabe quem digita a senha, ou seja, o ID do usuário é passado para o servidor após a senha. Pode ser uma caixa de identificação aleatória ao lado ou apenas um nome de usuário. Isso não importa. Mas o serviço sabe disso. Mas o servidor não apenas sabe um pouco disso, mas estritamente pode provar matematicamente que é ele.

Como isso funciona? Existe um back-end (algum tipo de serviço da web, site) e existe um serviço Pythia. O que o back-end faz e o que o serviço faz? Há uma chave privada k no serviço, mas também transfere sua chave pública para o back-end. O back-end do serviço envia não apenas o número mascarado a^r , como no protocolo Sphinx, mas também envia algum tipo de identificador de usuário ( UserID do usuário). O serviço multiplica o ID do usuário e a senha por sua chave privada e o resultado (UserID, a)^(r*k) do usuário (UserID, a)^(r*k) envia o back-end. Ele também envia de volta uma certa Proof , que pode ser usada pelo servidor para verificar se o servidor não foi hackeado, se está respondendo como deveria.

Depois, há um desmascaramento e o número y que resulta como resultado é colocado em um banco de dados. No banco de dados, não temos apenas um hash, mas um número, um ponto de uma curva elíptica.

Existem alguns pontos interessantes aqui:
- A capacidade do servidor de combinar o ID do usuário e a senha em um número. Isso é chamado de operação bilinear ou emparelhamento bilinear. Essa é uma matemática relativamente nova, que recentemente começou a ser usada. Ela tem todas as propriedades dos novos matemáticos nos últimos 30 anos, para que todos fiquem convencidos de que tudo está normal com isso.
- Mas a
Proof que envia o serviço é uma tecnologia bastante antiga. Isso é chamado de protocolo Schnorr . A geração de chave pública é a multiplicação de um ponto base por alguma chave secreta. O protocolo Schnorr prova que a chave secreta usada para gerar a chave pública foi usada para multiplicar a senha do usuário pelo mesmo número. Este protocolo já existe há muito tempo, é muito usado onde e permite que você prove. Isso é chamado de prova à prova de zero - o servidor não mostra sua chave pública, mas diz que a operação que eu executei foi executada por essa chave privada, com a qual originalmente concordamos.

Quais são as vantagens deste sistema?

E ela não tem muitos deles.
- O sistema não carrega o back-end. Como o back-end faz tudo, transforma a senha em um número, disfarça, envia e desmascara o resultado também.
- Se um banco de dados com esses números for roubado de você, a classificação de senhas também não fará sentido sem uma chave privada.
- O serviço Pythia pode bloquear tentativas de força bruta, o que significa que o back-end não precisa fazer isso em princípio. Se ele perceber que, com o mesmo ID do usuário, eles tentam executar essa operação de transformação várias vezes, ele pode simplesmente cortá-lo e bloqueá-lo no limite da taxa.
- Graças ao disfarce, o serviço não sabe nada sobre a senha. Cada vez que um novo número aleatório é enviado a ele. Somente o identificador de usuário permanece constante.
- Graças ao ZKP (prova de zero conhecimento), o back-end sempre sabe que foi o próprio serviço que ele entrou em contato.
- Se você tiver um banco de dados com hashes e sal, por exemplo, poderá migrar para uma solução perfeita para os usuários. Eles podem nem perceber nada. Em vez da senha do usuário, você pega seu hash, o direciona para Pythia e, no futuro, apenas usa este protocolo, obtém o número
y e o coloca novamente em seu banco de dados. O hash pode ser excluído. Cada vez que um usuário efetua login no seu sistema, esse protocolo será executado, um número será obtido como resultado, o qual você comparará com o que está no banco de dados. O sistema de autenticação em si permanecerá inalterado, pois os usuários efetuam login mais cedo e com as mesmas senhas, mesmo as mais fracas. Nesse caso, o sistema será muito mais seguro.

Mas estes não são todos os presentes.

Uma das principais características é que, mesmo que o serviço Pythia seja hackeado, é possível gerar uma nova chave privada. Em nosso banco de dados, um número é armazenado, não um hash. Se representarmos a chave antiga como o número k e a nova como o número k' , poderemos calcular um número chamado Atualizar token. Para fazer isso, multiplicamos o novo número pelo número inverso ao antigo. E com esse token de atualização, você pode percorrer o banco de dados de cada usuário e multiplicar esse número y pelo token de atualização. Depois de fazer isso, seu sistema continuará trabalhando com a nova chave privada no serviço remoto. Tudo acontece instantaneamente. Se ocorrer um desastre, seu banco de dados com senhas é roubado, você libera o token de atualização com o clique de um dedo e o fato de que hackers lhe roubaram se torna instantaneamente inútil. Você apenas percorre silenciosamente todos os registros em segundo plano, os atualiza e eles trabalham com a nova chave secreta para você. Os usuários geralmente nem percebem nada. I.e. Atualização contínua e invalidação instantânea do banco de dados de senhas são alguns dos principais recursos inovadores deste sistema.

Mas isso não é tudo.

O número que fica na base é grande y , é basicamente grande e parece bastante pseudo-aleatório, ou seja, é tão fácil não buscá-lo. Se transferirmos a funcionalidade que temos no back-end, por exemplo, para dispositivos clientes, telefones, podemos usar isso y para gerar chaves. Chamamos isso de BrainKey. Isso significa que o usuário digita a senha em algum lugar do telefone, também a disfarça e a envia ao serviço remoto. O serviço retorna um certo número y e y seguida, você pode usá-lo para gerar algumas chaves assimétricas. Assim, o usuário de sua senha pode obter um par de chaves. Isso é usado em todos os tipos de BrainWallets . É quando você digita a senha e obtém a carteira de bitcoin gerada para ela. Mas esse aplicativo não se limita a criptomoedas, é uma assinatura digital, alguns backups e recuperação de contas, ou seja, onde quer que a criptografia assimétrica seja usada, onde chaves assimétricas são necessárias. Tudo isso pode ser usado, mas, ao mesmo tempo, um par de chaves e, dependendo da necessidade, podem ser gerados quantos você desejar. Portanto, todos eles dependerão da senha do usuário, e isso é muito conveniente.

Em um barril de mel, não é sem uma mosca na pomada.

E os recursos desta tecnologia é que ela é muito nova. Ele usa uma curva elíptica, que é para operações bilineares ( BLS12-381 ). A própria matemática existe há algum tempo, mas essa curva específica, que é usada principalmente em nossa implementação, é usada apenas no ZCash, exceto nós. Assim, as bibliotecas que usam essa nova matemática podem ser contadas nos dedos de uma mão. Para trazer isso para o estado de produção, você precisa gastar uma certa quantidade de tempo e esforço. No entanto, o setor não fica parado e todas essas desvantagens são temporárias. Como conseqüência das duas primeiras propriedades, a velocidade dessas operações bilineares não é muito consistente com a matemática moderna, em particular elíptica, que todos usamos agora, quando usamos o protocolo TLS, quando usamos alguns sites. Isso está em torno de várias centenas de operações em um serviço em um núcleo. De fato, isso não nos impediu e, na primavera, implementamos esse protocolo, lançamos em produção e traduzimos todos os nossos registros, protegendo-os usando esse protocolo. Em princípio, estamos satisfeitos com o desempenho de nossas tarefas atuais; se necessário, criaremos outro nó com o serviço Pythia e, em princípio, você já pode jogar com tudo isso.
PHE

Mas pensamos se podemos fazer ainda melhor? É possível obter as propriedades que Pythia fornece usando a matemática de ontem? Nem amanhã, nem hoje, mas até ontem, que tem sido usado por muitos anos.

E, literalmente, em julho deste ano, os cientistas lançaram um novo protocolo chamado Serviços de criptografia simples protegidos por senha, ou PHE, para abreviar.

Este é Russell Lai , um cientista da Europa.
Qual é a vantagem deste serviço? Primeiro, ele usa a curva P-256 padrão, usada em todos os lugares, em todos os navegadores, produtos e em todos os lugares da curva padrão, que existe há muitos anos. Em segundo lugar, isso funciona 10 vezes mais rápido que Pythia e usa primitivas padrão. É meio difícil, mas você pode implementá-lo com suas próprias mãos sem usar nenhuma biblioteca obscura. Você pode usar o OpenSSL , ou o Bouncy Castle , qualquer coisa.

Mas funciona um pouco diferente. Novamente, há um back-end, há um serviço de PHE. O back-end tem uma chave pública, o serviço tem uma chave privada y . Ao contrário de Pythia, o processo de registro e o processo de verificação de senha são um pouco diferentes. Quando um novo usuário chega ao serviço e deseja se registrar, o que o back-end faz? Desde o início, ele pediu ao serviço PHE, por favor, me dê alguns dados que eu possa usar para registrar, algum tipo de registro de inscrição. O serviço diz OK e responde ao back-end com as seguintes coisas. Ele gera algum sal aleatório de 32 bytes ( sNonce ). Com base nesse sal e em sua chave privada y, ele gera dois números, vamos chamá-los de C0 e C1 . Também gera provas ( Proof ) de que esses dois números ou 2 pontos foram gerados precisamente usando sua chave privada y , usando o protocolo Schnorr (como nos protocolos anteriores). O back-end verifica Proof . Ainda não há senha aqui. O que o back-end faz? Por sua vez, ele também possui sua chave privada de cliente pessoal x e, após receber a senha do usuário, faz o mesmo que o serviço, apenas adiciona a senha lá. Leva cNonce aleatório (sal de cliente aleatório), uma senha e gera novamente 2 números HC0 e HC1 . Por que 2? Como o primeiro HC0 usado para autenticação, o segundo número HC1 mistura um número aleatório M multiplicado pela chave privada x ( MC ). O número M também tem 32 bytes de tamanho e pode ser usado posteriormente para criptografar dados do usuário (temos Serviços de Criptografia) ( observação do autor da nota: neste caso, a chave de criptografia será MC ). O número do MC estará disponível como chave somente depois que o usuário digitar a senha correta. Acontece que, no estágio de registro, você pode gerar não apenas um registro de autorização, mas também uma chave de criptografia, exclusiva para cada usuário, com a qual você pode criptografar seu perfil, alguns dados e outras coisas. Depois, o back-end simplesmente adiciona o que o serviço enviou e o que fez - soma esses pontos e obtém T0 e T1 . No primeiro caso, soma dois ( C0 + HC0 ) e no segundo três ( C1 + HC1 + MC ). E ele coloca na base 2 sais ( sNonce , cNonce ), com a ajuda dos quais esses números foram obtidos e 2 números ( T0 e T1 ), que resultaram como resultado da soma.

Assim, o processo de autenticação do usuário ocorre na ordem inversa. O usuário digita sua senha no back-end. O back-end calcula HC0 e, a partir do que possui no banco de dados, subtrai HC0 de T0 e envia o C0 resultante ao serviço junto com o sal do servidor. O serviço, conhecendo o salt do servidor, calcula o mesmo ponto em si e olha, coincide com o fato de que enviou ou não o back-end, se corresponder, a senha está correta e você pode respondê-la com o segundo número C1 , que subtrairá junto com o HC1 do número T1 e obtenha a chave de criptografia. Portanto, a senha do serviço PHE nem desaparece. Ele nem sai do back-end. É na forma de alguns pontos multiplicados pela chave privada do back-end. Ele nem existe como tal, mas, ao mesmo tempo, o serviço remoto pode concluir estritamente se essa senha está correta ou não e provar, além disso, que ele executou todos os cálculos usando sua chave privada y .

Quais recursos esse sistema possui?

A senha, como eu disse, não sai do back-end. Mas, diferentemente de Pythia, você precisa de uma chave privada no back-end. Bem, precisamos e precisamos, salve em algum lugar. PHE tem todas as funções básicas de Pythia:
- Você também pode emitir o token de atualização se algo acontecer com a chave privada;
- Você também pode percorrer todo o banco de dados, atualizar e tudo será como antes;
- proteção de pesquisa;
- o serviço não sabe nada sobre a senha;
- (Pythia , , , , PHE );
- .

...
… . . passw0rd.io . password , 18- , , zero trust, .. . , , .. Let's encrypt . , . CLI , . 2 SDK , GO .Net, .

:
- .
- .
- .

, .
?
37. ?

.
Q: , ! . , Pythia update token, ? private key . update token? Ou não?
A: , update token- .
Q: . - update token-, Private key ?
A: , update token-, , - , , , update token. , .. .
Q: , , , .
A: .. .
Q: , , , - Pythia - , , , ?
A: .
Q: ?
A: , Pythia . I.e. , .
Q: ( ) bcrypt ?
A: , , , .
Q: , . ? , …
A: password
Q: password ? Fogo! Geralmente.
A: 123456 , 12345, 123456.
Q: . Pythia , PHE .
A: , .
Q: . . ? production ?
A: . Ah! Pythia.
Q: Pythia, , ?
A: .
Q: , ?
A: .
Q: , , !
A: SDK, .
Q: , , , , .. - , ? ? ?
A: , , , .. PHE, , 5 2 , 2 5 . , . PHE ( , ), , 10 , .
Q: .. - , - ? ?
A: . rate limiting, , .
Q: .. , ?
A: .
Q: . , .. Pythia (), , ? ?
A: , , .
Q: , update ?
A: , Pythia , , - - , , , )
A: ? ! . , , PHE, , .
Conclusões
PHE ( ) + — ( , , ) ( ). PHE , .
:
, .
Scratch Virgil Security , , !
( )?
UPD : Scratch . . , . .