A matemática em Gamedev é simples. Triangulação e Triangle.Net em Unity

Olá pessoal! Meu nome é Grisha e sou o fundador da CGDevs. A matemática é uma ferramenta muito interessante no desenvolvimento de jogos. Mas se dissermos que é difícil gerenciar sem entender vetores e matrizes , os algoritmos de triangulação não são uma coisa tão necessária, mas com a ajuda deles, um grande número de problemas interessantes é resolvido. Hoje eu gostaria de falar sobre uma ferramenta bastante importante em geometria computacional, como triangulações e sua aplicação na indústria de jogos. Além disso, escrevi uma porta e alguns invólucros para a excelente biblioteca Triangle.Net para Unity. Se estiver interessado - bem-vindo ao gato. Link para o github anexado.

O que é triangulação?

No caso geral, a triangulação é uma partição de um objeto geométrico em triângulos. Este conceito em si é bastante simples. Um exemplo básico de triangulação no caso de mecanismos de jogos é uma malha. A rigor, uma malha pode consistir não apenas em triângulos, mas nos mecanismos de jogo, por várias razões, é uma malha composta por triângulos.



As triangulações são diferentes, mas um dos tipos mais populares de triangulação é a triangulação de Delaunay. Esse tipo de triangulação se distingue pela propriedade que, no círculo circunscrito em torno de cada triângulo, apenas os vértices desse triângulo estão.

Por que eles são necessários?

Em geral, fora da indústria de jogos, um grande número de tarefas é resolvido com a ajuda de triangulações. No game dev, a primeira tarefa que vem à mente é a malha de navegação. Navmesh é uma estrutura de dados que determina quanto espaço um jogador pode percorrer. Evita tarefas computacionais complexas, como determinar colisões com parte do ambiente.

O segundo problema interessante que pode ser resolvido usando a triangulação de Delaunay no desenvolvimento de jogos é a geração de terrenos e objetos representados como um conjunto de pontos. A principal vantagem da triangulação de Delaunay nesse caso é que, com base em suas propriedades, ele permite evitar triângulos muito nítidos que interferem e criam artefatos no tirrain.



Além disso, usando triangulação e algoritmos restritos de Delaunay, como o segundo algoritmo de Chew e o algoritmo de Ruppert, você pode gerar malhas ainda melhores para tirrains e boas malhas para outra aplicação - o método dos elementos finitos.

O método dos elementos finitos em si é um dos métodos pelos quais os problemas da física aplicada são resolvidos. No gamedev, ele permite resolver muitos problemas associados à simulação de deformações, simulações de fluidos e outras utilizadas para fins especiais. efeitos Normalmente, para gravar efeitos em animação, uma vez que, em tempo real, o método possui uma complexidade computacional muito alta. Um detalhe importante ao usar o método é que o erro do método depende dos ângulos dos triângulos na grade. Se houver ângulos muito nítidos na grade, o método apresenta um erro enorme; por esse motivo, os algoritmos listados acima são necessários.



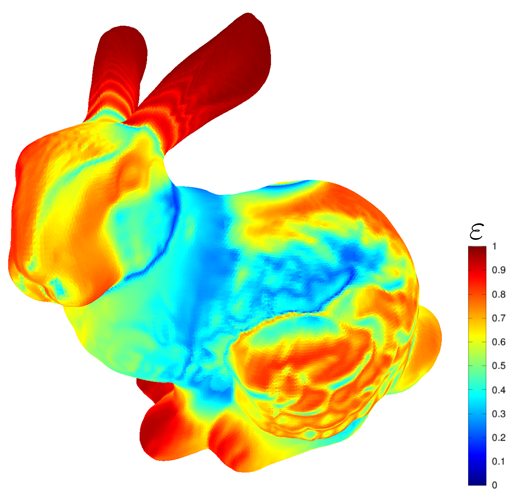
E, é claro, em geral, geração de malha procedural. Como exemplo, um projeto do github mostra uma cena com a capacidade de desenhar malhas. Alguns quebra-cabeças físicos usam esse aplicativo como mecânica básica. Além disso, os algoritmos de triangulação permitem usar a geração procedural para resolver problemas como destrutibilidade processual e assim por diante.

Além das gamedev, triangulações são usadas em redes, visão computacional, vários algoritmos analíticos e em quais problemas da geometria computacional, como combinar e eliminar polígonos uns dos outros (o que geralmente é útil em problemas que surgem no desenvolvimento de jogos)

Clipe de Orelha com Orifícios

Talvez um dos algoritmos de triangulação mais simples. Ele não fornece a melhor grade e tem a maior complexidade computacional O (n ^ 2) no pior caso.

Você pode ler mais sobre isso neste artigo.

Algoritmo de Bowyer - Watson

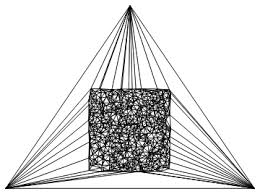
Um algoritmo que gera a triangulação de Delaunay sobre um conjunto de pontos. Em geral, como na maioria dos algoritmos de Delaunay, se implementado corretamente, a complexidade algorítmica é O (n log n), onde n é o número de vértices. Mas, em alguns casos, pode levar O (n ^ 2).

As desvantagens em relação ao corte de orelha são que esse algoritmo cria triangulação convexa e, na implementação básica, não envolve buracos na grade resultante.

Processamento de refinamento em Delaunay

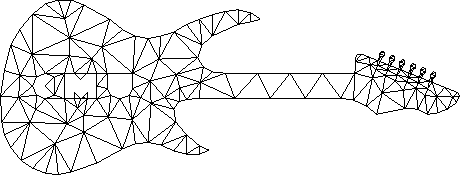
O segundo algoritmo de Chew e o algoritmo de Ruppert são algoritmos que permitem inserir restrições na triangulação de Delaunay e definir o ângulo mínimo do triângulo na grade. Um detalhe importante dos algoritmos é que eles podem entrar em um loop infinito e garantir resultados em ângulos entre aproximadamente 20,7 e 29 graus. A capacidade de definir um ângulo mínimo é importante na solução dos problemas descritos acima.

O segundo algoritmo do Chew é implementado no pacote gratuito www.cs.cmu.edu/~quake/triangle.html e sua porta no .Net archive.codeplex.com/?p=triangle

Triangle.Net for Unity

Bem, como com a ajuda das triangulações você pode resolver muitas tarefas interessantes, nas férias eu queria implementar meu invólucro para o Unity, para ter sempre uma ferramenta útil à mão. Nesta implementação, o algoritmo de triangulação funciona em média para O (n) e, na pior das hipóteses, para O (n * log n), onde n é o número de vértices. Por exemplo, ao testar vértices de 1kk espalhados aleatoriamente por um quadrado, as unidades no editor no Intel Core i7-8700 construíram uma grade em média 7,56 segundos.

As principais diferenças da biblioteca original na presença de métodos de extensão personalizados para o Unity, bem como a substituição de double por float em toda a biblioteca (+ alguns operadores específicos para fundição) O dobro na unidade, não faz muito sentido. Se considerarmos simulações físicas, eu usaria um aplicativo separado em uma biblioteca positiva, e o resultado dos cálculos já deu ao Unity apenas para visualização. E também renomeou o tipo de malha para TriangleNetMesh para não derrubar em relação à malha do Unity. Sim, eles já estão em um espaço de nome diferente, mas, no entanto, acho que os recém-chegados ficariam um pouco abalados pelo fato de que, com a ajuda de um Mesh, conseguimos outro.

A essência da biblioteca é que você deve primeiro especificar o chamado polígono. Então, com base nisso, já gere a malha. Para que isso funcione com estruturas de dados de unidade, vários métodos de extensão foram introduzidos.



Para demonstração e exemplo de uso, uma cena de demonstração especial foi feita com a capacidade de desenhar malhas. Você pode se familiarizar com ele e a porta da biblioteca no projeto github.

Obrigado pela atenção! Espero que a porta e o artigo sejam úteis para alguém e fique um pouco mais claro por que a triangulação e o conhecimento da matemática como um todo são necessários. Tentarei continuar divulgando aplicativos e métodos para resolver vários problemas matemáticos no desenvolvimento de jogos. Na própria geometria computacional, ainda existem muitas coisas interessantes, mas além disso, ainda existem muitas outras seções interessantes da matemática superior.