Previsão novamente, parte 1

Considere a previsão de séries temporais. Vamos tentar prever gráficos de cotações ou algo mais que seja útil.



Vamos tomar como base a previsão apresentada no artigo O modelo de previsão de séries temporais para a amostra de semelhança máxima: explicação e exemplo (este artigo não é meu). O breve argumento é que o segmento mais semelhante do gráfico é procurado à esquerda da previsão entre o histórico passado e, desse melhor antigo, os valores à direita do gráfico são tomados e usados ​​como previsão.

Eu irei mais longe. Ao calcular a previsão, considerarei não um caso que seja o melhor em correlação, mas um pacote dos melhores. E a previsão será a média dos resultados deste pacote. Isso tornará possível entender que o valor encontrado é uma regularidade, e não uma coincidência acidental com a previsão desejada, ou um desvio aleatório se a previsão se desviar do valor real.

Usar a melhor opção única, conforme mencionado no artigo, não está correto, além de determinar a distribuição de probabilidade com um valor dessa distribuição. Se você gerar um gráfico muito grande de dados aleatórios e iniciar uma pesquisa neles, certamente haverá segmentos correlatos neles, e mesmo possivelmente com um coeficiente de 0,9999, mas não é necessário que segmentos semelhantes continuem a seguir esses segmentos - ainda é necessário. tudo é aleatório. E você precisa pegar apenas um pacote desses segmentos e calcular que a variação dos dados subseqüentes é menor que a variação formada a partir de uma amostra aleatória desses dados. E se a dispersão do pacote for menor - então esta é a previsão. Embora essa também não seja uma representação precisa de possíveis erros, isso é suficiente por enquanto.

I.e. previsão não é qual princípio de amostragem e correlação dos segmentos comparados que usamos, o principal é que, como resultado da aplicação dessa amostra, a variação dos valores desejados seria menor do que como resultado da amostragem aleatória.

Além disso, a variação deste pacote permitirá avaliar qual é melhor usar a opção de seleção de casos anteriores. Afinal, é possível selecionar nem sempre um segmento de dados correlacionados e nem sempre usar a correlação de Pearson. E essa escolha pode ser feita para cada ponto previsto separadamente. Para que tipo de amostra a variação é menor, essa opção é melhor para o ponto atual.

Qual o tamanho do pacote? Isso se baseia na questão dos intervalos de confiança. Para não carregar muito, há uma menção de que é melhor usar pelo menos 30 exemplos para determinar o valor médio. Se houver um excesso de dados de teste, eu levaria pelo menos 100.

A proporção dos desvios padrão da amostra de acordo com o algoritmo e o aleatório pode ser chamada de coeficiente teórico de sucesso do algoritmo de previsão para o ponto atual para fins de comparação com outros algoritmos de amostragem ou para determinar a utilidade dessa previsão em geral, enquanto o valor real ainda não está disponível.



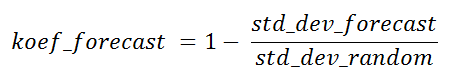
Este coeficiente pode, em alguns casos, assumir valores negativos. Os pontos em que isso ocorre são de pouco interesse, assim como os pontos com um coeficiente zero. No caso de 100% de previsibilidade, será igual a um.

Vamos passar para exemplos práticos, novamente a partir desse artigo. Depois de corrigir os pequenos erros, obtemos o seguinte resultado, consistente com esse artigo e esse algoritmo:

cálculo da previsão no momento de 1/9/2012 23:00 posição 52631
valores totais verificados quanto à similaridade 2184
a melhor correlação 0.958174 posição 52295
coeficientes de transferência alfa (1/2) 1.03117 -11.1992
erro de previsão do fato mape 5,210%

mape - o termo do artigo original Mean Percentage Absolute Error, é calculado pela fórmula
Abs (Previsão - Fato) / Fato

E agora vamos fazer uma seleção de não apenas uma das melhores semelhanças, mas pacotes das melhores e de tudo para prever um momento no tempo e ver o que acontece:

0 corr 0.958174 pos 52295 mape 5.210%
1 corr 0.953571 pos 52151% 6.566%
2 corr 0.953532 pos 45599 mape 11.642%
3 corr 0.951462 pos 45743 código 7.033%
4 corr 0.950921 pos 45575 tipos 3.300%
5 corr 0.950789 pos 38687 código 3.538%

O valor de correlação aqui muda de valor para valor insignificante. Ao mesmo tempo, o valor do resultado da previsão varia de 3% a 11%. I.e. que 5% iniciais nada mais são do que uma coincidência, podem ser 11% e 3%.

Sob as condições de similaridade especificadas naquele artigo, os valores de 2184 podem ser comparados no total. Destas, peguei um pacote dos melhores em 1500 peças, classificadas na ordem de correlação decrescente, e a exibi em um gráfico. A correlação neste pacote dos melhores 0,958 caiu para 0,715 da esquerda para a direita. Mas a flutuação do resultado praticamente não mudou:



Pode-se observar que a dependência do resultado na correlação é muito baixa, mas parece existir. Em geral, pegamos um pacote com os 100 principais valores e calculamos a previsão, como mencionei, pela média desse pacote. O resultado é o seguinte: mape 5.824%, stddev mape 7.035% . Mas esses 5,8% não são mais uma coincidência, mas a média da distribuição - a previsão mais provável. O desvio padrão do mape é maior que o próprio mape, mas isso ocorre porque o mape possui uma distribuição não simétrica.

Também calculei a mesma previsão, mas usando uma amostra aleatória condicional, mais precisamente, simplesmente calculando a média de todas as opções possíveis, o resultado do mape foi de 8,246% . Por amostragem aleatória, o erro é um pouco maior, mas esse valor ainda está dentro do intervalo da dispersão calculada a partir da melhor amostra. Para o ponto calculado, o coeficiente teórico de previsão indicado por mim é próximo de zero, mais precisamente koef_forecast = -0,041 . Eu não contei do stddev mape (inclui a previsão real), mas dos valores absolutos da previsão, se você olhar para o programa, os números iniciais para ele serão dados lá.

Mas isso ocorre se o carimbo de data / hora mencionado no artigo original. Porém, se considerarmos “04/09/2012 23:00” (mês / dia / ano), o coeficiente teórico de eficiência será koef_forecast = 0,21 e mape = 3,126%, mape_rand = 7,147% . I.e. O koef_forecast mostrou antecipadamente que o ponto atual será calculado com mais precisão que o anterior. A essência da utilidade desse coeficiente é que você pode, pelo menos de alguma forma, avaliar o resultado antes mesmo de obter os dados reais, porque dados reais não participam dos mesmos. Quanto mais alto, melhor. Eu já mencionei que um ponto absolutamente previsto terá um coeficiente de um.

Você pode ver como todos esses números mudam no meu programa de demonstração no Qt C ++. Lá você pode escolher a data e o tamanho do pacote: as fontes no github

Os melhores valores são selecionados de acordo com o seguinte algoritmo:

inline void OrdPack::add_value(double koef, int i_pos) { if (std::isfinite(koef)==false) return; if (koef <= 0.0) return; if (mmap_ord.size() < ma_count_for_pack) { if (mmap_ord.size()==0) mi_koef = koef; mi_koef = std::min(mi_koef, koef); mmap_ord.insert({-koef,i_pos}); } else if (koef > mi_koef) { mmap_ord.insert({-koef,i_pos}); while (mmap_ord.size() > ma_count_for_pack) mmap_ord.erase(--mmap_ord.end()); mi_koef = -(--mmap_ord.end())->first; } } 

Não há sentido em postar toda a fonte aqui, não é complicado lá e com comentários. A base do procedimento MainWindow :: to_do_test () no arquivo mainwindow.cpp .

Por enquanto, continuarei tentando prever algo na próxima parte.

PS. Por favor, deixe seus comentários sobre se tudo está claro sobre o que está faltando. Já formulei um plano aproximado para o que escrever a seguir, mas com seus comentários, farei melhor.