Teoria da felicidade. A estatística como forma científica de não saber nada

Continuo familiarizando os leitores de Habr com os capítulos de seu livro "Theory of Happiness", com o subtítulo "Fundamentos matemáticos das leis da maldade". Este livro científico ainda não foi publicado, informando de maneira muito informal sobre como a matemática permite que você olhe para a vida do mundo e das pessoas com um novo grau de conscientização. É para aqueles que estão interessados ​​em ciência e para aqueles que estão interessados ​​na vida. E como nossa vida é complexa e, em geral, imprevisível, a ênfase no livro está principalmente na teoria das probabilidades e nas estatísticas matemáticas. Aqui os teoremas não são provados e os fundamentos da ciência não são dados; isso não é de forma alguma um livro, mas o que é chamado ciência recreativa. Mas é precisamente essa abordagem quase lúdica que nos permite desenvolver a intuição, animar as palestras para os alunos com exemplos vívidos e, finalmente, explicar aos não matemáticos e nossos filhos que encontramos coisas tão interessantes em nossa ciência seca.


Este capítulo é sobre estatísticas, clima e até filosofia. Não se preocupe, só um pouquinho. Não é mais possível usar o tabletalk em uma sociedade decente.

Os números enganam, principalmente quando eu os faço; nesta ocasião, a afirmação atribuída a Disraeli é verdadeira: "Existem três tipos de mentiras: mentiras, mentiras descaradas e estatísticas".
Mark Twain

Quantas vezes no verão planejamos ir ao ar livre, passear no parque ou fazer um piquenique, e então a chuva quebra nossos planos, aprisionando-nos em casa! E bem, se isso aconteceu uma ou duas vezes por temporada, às vezes parece que o tempo está seguindo o fim de semana, chegando ao sábado ou domingo de novo e de novo!

Um artigo relativamente recente foi publicado por pesquisadores australianos: "Ciclos semanais de pico de temperatura e intensidade das ilhas termais urbanas". Ela foi escolhida pela mídia e reimprimiu os resultados com o seguinte título: “Você não acha! Os cientistas descobriram que o clima nos finais de semana é realmente pior do que nos dias úteis. ” O artigo citado fornece estatísticas sobre temperatura e precipitação ao longo de muitos anos em várias cidades da Austrália e, de fato, revela uma diminuição da temperatura em determinadas horas do sábado e domingo. Depois disso, é dada uma explicação que conecta o clima local ao nível de poluição do ar devido ao aumento do fluxo de tráfego. Pouco antes disso, um estudo semelhante foi realizado na Alemanha e levou a aproximadamente as mesmas conclusões.

Concordo, frações de um grau é um efeito muito sutil. Reclamando o mau tempo no tão esperado sábado, estamos discutindo se o dia estava ensolarado ou chuvoso, essa circunstância é mais fácil de registrar e, mais tarde, para lembrar, sem sequer ter instrumentos precisos. Conduziremos nosso pequeno estudo sobre esse tópico e obteremos um resultado maravilhoso: podemos dizer com segurança que não sabemos se o dia da semana e o clima estão relacionados em Kamchatka. Os estudos com um resultado negativo geralmente não se enquadram nas páginas das revistas e nos feeds de notícias, mas é importante que você e eu entendamos com que base eu, em geral, posso dizer com segurança algo sobre processos aleatórios. E, nesse sentido, um resultado negativo não é pior que um resultado positivo.

Uma palavra em defesa das estatísticas

As estatísticas são culpadas pela massa dos pecados: nas mentiras e nas possibilidades de manipulação e, finalmente, na incompreensibilidade. Mas eu realmente quero reabilitar esta área do conhecimento, para mostrar quão difícil é a tarefa para a qual se destina e quão difícil é entender a resposta que a estatística dá.

A teoria da probabilidade usa conhecimento preciso de variáveis ​​aleatórias na forma de distribuições ou cálculos combinatórios abrangentes. Enfatizo mais uma vez que é possível ter conhecimento preciso de uma variável aleatória. Mas e se esse conhecimento exato for inacessível para nós, e a única coisa que temos à nossa disposição é a observação? O desenvolvedor do novo medicamento possui um número limitado de testes, o criador do sistema de controle de fluxo de tráfego possui apenas uma série de medições na estrada real, o sociólogo tem os resultados de pesquisas e, além disso, pode ter certeza de que, ao responder a algumas perguntas, os respondentes apenas menti.

É claro que uma observação não dá nada. Dois - um pouco mais do que nada, três, quatro ... cem ... quantas observações você precisa para obter algum conhecimento de uma variável aleatória da qual possa ter certeza com precisão matemática? E que tipo de conhecimento será esse? Provavelmente, ele será apresentado na forma de uma tabela ou de um histograma que permita avaliar alguns parâmetros de uma variável aleatória; eles são chamados de estatística (por exemplo, domínio de definição, média ou variância, assimetria, etc.). Talvez olhando o histograma seja capaz de adivinhar a forma exata da distribuição. Mas atenção! - todos os resultados da observação serão variáveis ​​aleatórias! Enquanto não tivermos conhecimento exato da distribuição, todos os resultados da observação nos fornecerão apenas uma descrição probabilística do processo aleatório! Uma descrição aleatória de um processo aleatório ainda não seria confundida aqui, ou mesmo desejaria confundir intencionalmente!

O que faz da estatística matemática uma ciência exata? Seus métodos nos permitem concluir nossa ignorância em uma estrutura claramente limitada e fornecer uma medida computável de confiança de que, dentro dessa estrutura, nosso conhecimento é consistente com os fatos. Essa é a linguagem na qual se pode raciocinar sobre variáveis ​​aleatórias desconhecidas, para que o raciocínio faça sentido. Essa abordagem é muito útil em filosofia, psicologia ou sociologia, onde é muito fácil envolver-se em longas discussões e raciocínios sem nenhuma esperança de obter conhecimento positivo e, principalmente, prova. Muita literatura é dedicada ao processamento estatístico de dados competente, porque é uma ferramenta absolutamente necessária para médicos, sociólogos, economistas, físicos, psicólogos ... em uma palavra, para todos os cientistas que pesquisam o chamado "mundo real", que difere do ideal matemático apenas no grau de nossa ignorância sobre ele.

Agora, dê uma outra olhada na epígrafe deste capítulo e perceba que as estatísticas, que são tão depreciativamente chamadas de terceiro grau de mentiras, são as únicas coisas que as ciências naturais têm. Não é essa a principal lei da maldade do universo! Todas as leis da natureza conhecidas por nós, do físico ao econômico, são baseadas em modelos matemáticos e em suas propriedades, mas são verificadas por métodos estatísticos durante medições e observações. Na vida cotidiana, nossa mente faz generalizações e observa padrões, isola e reconhece imagens repetidas; provavelmente é o melhor que o cérebro humano pode fazer. É exatamente isso que a inteligência artificial está ensinando atualmente. Mas a mente economiza sua força e está inclinada a tirar conclusões de observações individuais, não se preocupando muito com a precisão ou validade dessas conclusões. Nesta ocasião, há uma maravilhosa declaração autoconsistente do livro de Stephen Brast, Isola: “Todo mundo tira conclusões gerais de um exemplo. Pelo menos eu faço exatamente isso . E enquanto falamos de arte, natureza dos animais de estimação ou discutimos política, você não pode se preocupar muito com isso. No entanto, ao construir um avião, organizar um serviço de despacho no aeroporto ou testar um novo medicamento, você não pode mais se referir ao fato de que "parece-me", "a intuição diz" e "tudo acontece na vida". Aqui você deve limitar sua mente à estrutura de métodos matemáticos rigorosos.

Nosso livro não é um livro didático, e não estudaremos os métodos estatísticos em detalhes e nos limitaremos a apenas uma coisa - a técnica de testar hipóteses. Mas eu gostaria de mostrar o curso do raciocínio e a forma dos resultados característicos deste campo do conhecimento. E, talvez, alguns dos leitores, o futuro aluno, não apenas entendam por que o atormentam com estatísticas, com todos esses diagramas de QQ, distribuições teF, mas surge outra pergunta importante: como é possível saber o que - certamente sobre um acidente? E o que exatamente aprendemos usando estatísticas?

Três baleias de estatísticas

Os principais pilares da estatística matemática são a teoria da probabilidade, a lei dos grandes números e o teorema do limite central .

A lei dos grandes números, em uma interpretação livre, sugere que um grande número de observações de uma variável aleatória quase certamente reflete sua distribuição , de modo que as estatísticas observadas: média, variância e outras características tendem a exigir valores correspondentes à variável aleatória. Em outras palavras, o histograma dos valores observados com um número infinito de dados quase certamente tende à distribuição que podemos considerar verdadeira. É essa lei que conecta a interpretação da frequência “cotidiana” da probabilidade e a teórica, como medidas em um espaço de probabilidade.

O teorema do limite central, novamente, em uma interpretação livre, diz que uma das formas mais prováveis ​​de distribuição de uma variável aleatória é uma distribuição normal (gaussiana). A redação exata soa diferente: o valor médio de um grande número de variáveis ​​aleatórias reais distribuídas de forma idêntica, independentemente de sua distribuição, é descrito pela distribuição normal. Esse teorema é geralmente provado usando métodos de análise funcional, mas veremos mais adiante que ele pode ser entendido e até expandido, introduzindo o conceito de entropia como uma medida da probabilidade de um estado do sistema: uma distribuição normal tem a maior entropia com o menor número de restrições. Nesse sentido, é ideal ao descrever uma variável aleatória desconhecida, ou uma variável aleatória, que é uma combinação de muitas outras variáveis ​​cuja distribuição também é desconhecida.

Essas duas leis fundamentam estimativas quantitativas da confiabilidade de nosso conhecimento com base em observações. Aqui estamos falando sobre confirmação estatística ou refutação da suposição, que pode ser feita a partir de alguns fundamentos comuns e modelo matemático. Isso pode parecer estranho, mas por si só, as estatísticas não produzem novos conhecimentos. Um conjunto de fatos se transforma em conhecimento somente depois de criar conexões entre fatos que formam uma certa estrutura. São essas estruturas e relacionamentos que nos permitem fazer previsões e fazer suposições gerais baseadas em algo que vai além da estatística. Tais suposições são chamadas de hipóteses . É hora de relembrar uma das leis da merfologia, o postulado Persigue :

O número de hipóteses razoáveis ​​que explicam qualquer fenômeno é infinito.

A tarefa da estatística matemática é limitar esse número infinito, ou melhor, reduzi-lo a um, e não necessariamente verdadeiro. Para avançar para uma hipótese mais complexa (e muitas vezes mais desejável), é necessário, usando dados observacionais, refutar a hipótese mais simples e mais geral, ou reforçá-la e abandonar o desenvolvimento da teoria. A hipótese frequentemente testada dessa maneira é chamada nula , e há um sentido profundo disso.

O que pode funcionar como uma hipótese nula? Em certo sentido, qualquer coisa, qualquer afirmação, mas com a condição de que possa ser traduzida para o idioma da medida. Na maioria das vezes, a hipótese é o valor esperado de algum parâmetro, que se transforma em uma variável aleatória durante a medição ou a ausência de uma conexão (correlação) entre duas variáveis ​​aleatórias. Às vezes, assume-se o tipo de distribuição, um processo aleatório, algum modelo matemático é proposto. A formulação clássica da pergunta é a seguinte: as observações nos permitem rejeitar a hipótese nula ou não? Mais precisamente, com que certeza podemos dizer que as observações não podem ser obtidas com base na hipótese nula? Além disso, se não formos capazes de provar, com base em dados estatísticos, que a hipótese nula é falsa, ela será aceita como verdadeira.

E aqui você pode pensar que os pesquisadores são forçados a cometer um dos erros lógicos clássicos, que leva o sonoro nome latino ad ignorantiam. Este é um argumento da verdade de uma afirmação, baseada na falta de evidência de sua falsidade. Um exemplo clássico são as palavras proferidas pelo senador Joseph McCarthy quando ele foi convidado a apresentar fatos para apoiar sua acusação de que uma certa pessoa é comunista: “Tenho pouca informação sobre esse assunto, exceto a declaração geral das autoridades competentes de que não há nada em seu dossiê. para excluir seus laços com os comunistas " . Ou ainda mais: "O Pé Grande existe, já que ninguém provou o contrário . " Identificar a diferença entre uma hipótese científica e truques semelhantes é o assunto de todo um campo da filosofia: a metodologia do conhecimento científico . Um de seus resultados impressionantes é o critério de falsificabilidade , apresentado pelo notável filósofo Karl Popper na primeira metade do século XX. Esse critério foi criado para separar o conhecimento científico do não científico e, à primeira vista, parece paradoxal:

Uma teoria ou hipótese pode ser considerada científica apenas se existir, mesmo hipoteticamente, uma maneira de refutá-la.

O que não é a lei da maldade! Acontece que qualquer teoria científica é automaticamente potencialmente incorreta, e uma teoria verdadeira "por definição" não pode ser considerada científica. Além disso, ciências como matemática e lógica não satisfazem esse critério. No entanto, não se referem às ciências naturais , mas às formais , que não exigem um teste de falsificabilidade. E se adicionarmos mais um resultado ao mesmo tempo: o princípio da incompletude de Gödel, que afirma que, dentro de qualquer sistema formal, é possível formular uma afirmação que não pode ser provada nem refutada, pode ficar claro por que, em geral, se envolver em toda essa ciência. No entanto, é importante entender que o princípio da falsificabilidade de Popper não diz nada sobre a verdade de uma teoria, mas apenas se é científica ou não. Pode ajudar a determinar se uma teoria fornece uma linguagem na qual faz sentido falar sobre o mundo ou não.

Mas, ainda assim, por que, se não podemos rejeitar a hipótese com base em dados estatísticos, temos o direito de aceitá-la como verdadeira? O fato é que a hipótese estatística não é extraída do desejo ou preferências do pesquisador, deve seguir quaisquer leis formais gerais. Por exemplo, a partir do Teorema do Limite Central ou do princípio da entropia máxima. Essas leis refletem corretamente o grau de nossa ignorância , sem acrescentar, desnecessariamente, suposições ou hipóteses desnecessárias. Em certo sentido, esse é um uso direto do famoso princípio filosófico conhecido como navalha de Occam :

O que pode ser feito com base em menos suposições não deve ser feito com base em mais.

Assim, quando aceitamos a hipótese nula, com base na ausência de sua refutação, mostramos formal e honestamente que, como resultado do experimento, o grau de nossa ignorância permaneceu no mesmo nível . No exemplo do Pé Grande, explícita ou implicitamente, assume-se o contrário: a falta de evidência de que essa criatura misteriosa não parece ser algo que possa aumentar o grau de conhecimento sobre ela.

Em geral, do ponto de vista do princípio da falsificabilidade, qualquer afirmação sobre a existência de algo não é científica, porque a falta de evidência não prova nada. Ao mesmo tempo, a afirmação da ausência de qualquer coisa pode ser facilmente refutada ao fornecer uma cópia, evidência indireta ou provar a existência de uma construção. E, nesse sentido, um teste de hipótese estatística analisa alegações da ausência do efeito desejado e pode fornecer, em certo sentido, uma refutação precisa dessa afirmação. É exatamente isso que o termo “hipótese nula” é totalmente justificado: contém o conhecimento mínimo necessário sobre o sistema.

Como confundir estatísticas e como desvendar

É muito importante enfatizar que, se as estatísticas indicarem que a hipótese nula pode ser rejeitada, isso não significa que, assim, provamos a verdade de qualquer hipótese alternativa.As estatísticas não devem ser confundidas com a lógica; aí está uma massa de erros sutis, especialmente quando probabilidades condicionais para eventos dependentes entram em jogo. Por exemplo: é muito improvável que uma pessoa possa ser o Papa ($$~ 1 / 7 bilhões) follow daí que o Papa João Paulo II não era um homem? A afirmação parece absurda, mas, infelizmente, uma conclusão "óbvia" é igualmente falsa: o teste mostrou que um teste móvel para o teor de álcool no sangue não dá mais$\sim 1/7$$$1 % dos resultados falso positivo e falso negativo, portanto, em$1\%$$$98 % dos casos, ele identificará corretamente um motorista bêbado. Vamos testar$98\%$$$1000 drivers e deixe$1000$$$100 deles estarão realmente bêbados. Como resultado, obtemos$100$$$900 × 1 % = 9 falsos positivos e$900\times1\%=9$$$100 × 1 % = 1 resultado falso-negativo: ou seja, para um bêbado que entrou, haveria nove motoristas aleatoriamente acusados ​​inocentemente. O que não é a lei da maldade! A paridade será observada apenas se a proporção de motoristas bêbados for igual a$100\times1\%=1$$$1 / 2 , ou se a proporção da fracção de falsos positivos e falsos resultados negativos será perto da real em relação aos condutores bebido sóbrio. Além disso, quanto mais sobriamente pesquisada a nação, mais injusto será o uso do dispositivo descrito por nós!Aqui nos deparamos comeventos dependentes. Lembre-se de que a definição de probabilidade de Kolmogorov falou de um método para adicionar a probabilidade de combinar eventos: a probabilidade de combinar dois eventos é igual à soma de suas probabilidades menos a probabilidade de sua interseção. No entanto, essas definições não dizem como é calculada a probabilidade da interseção de eventos. Para isso, é introduzido um novo conceito: aprobabilidade condicionale a dependência de eventos um do outro vêm à tona.$1/2$


A probabilidade de interseção dos eventos A e B é definida como o produto da probabilidade do evento B e a probabilidade do evento $$A , se for sabido que um evento ocorreu$A$$$$B$ :

$$

$$P(A \cap B) = P(B)P(A|B).$$

Agora você pode determinar a independência dos eventos de três maneiras equivalentes: Eventos $$$A$ e $$B independente se$B$$$P ( A | B ) = P ( A ) , ou$P(A|B) = P(A)$$$P ( B | A ) = P ( B ) , ou$P(B|A) = P(B)$$$$P(A\cap B) = P(A)P(B)$ .
Isso completa a definição formal de probabilidade iniciada no primeiro capítulo.

A interseção é uma operação comutativa, ou seja,$$$P(A\cap B) = P(B\cap A)$ . Isso implica imediatamente o teorema bayesiano:

$$

$$P(A|B)P(B) = P(B|A)P(A),$$

que pode ser usado para calcular probabilidades condicionais.

Em nosso exemplo com motoristas e um teste de álcool, temos eventos:$$A - o motorista está bêbado,$A$$$O teste B deu um resultado positivo. Probabilidades:$B$$$P ( A ) = 0,1 - a probabilidade de o motorista parado estar bêbado;$P(A) = 0.1$$$P ( B | A ) = 99 % - a probabilidade de o teste dar um resultado positivo se for sabido que o motorista está bêbado (excluído$P(B|A) = 99\%$$$1 % de falso negativo)$1\%$$$P ( A | B ) = 99 % - a probabilidade de que o teste bebesse, se o resultado desse resultado positivo (excluído$P(A|B) = 99\%$$$1 resultado falso positivo). Calculamos$1%$$$$P (B)$ - a probabilidade de obter um resultado positivo na estrada:

$$

$$P (B) = \ frac {P (A) P (A | B)} {P (B | A)} = P (A) = 0,1$$

Agora, nosso raciocínio se formalizou e, como você sabe, talvez para algumas pessoas mais compreensíveis. O conceito de probabilidade condicional permite raciocinar logicamente na linguagem da teoria das probabilidades. Não é de surpreender que o teorema de Bayes tenha encontrado ampla aplicação na teoria da decisão, em sistemas de reconhecimento de padrões, em filtros de spam, em programas que testam testes de plágio e em muitas outras tecnologias da informação.

Esses exemplos são cuidadosamente entendidos pelos estudantes de exames médicos ou práticas legais. Receio, porém, que nem estatística matemática nem teoria das probabilidades sejam ensinadas a jornalistas ou políticos, mas elas apelam com entusiasmo aos dados estatísticos, os interpretam livremente e trazem o conhecimento adquirido para as massas. Portanto, exorto meu leitor: eu mesmo descobri a matemática, me ajude a descobrir por outra! Não vejo outro antídoto para a ignorância.

Medimos nossa credulidade

Consideraremos e aplicaremos na prática apenas um dos muitos métodos estatísticos: testar hipóteses estatísticas. Para aqueles que já vincularam suas vidas às ciências naturais ou sociais, não haverá algo surpreendentemente novo nesses exemplos.

Suponha que medimos repetidamente uma variável aleatória com um valor médio $$$\ mu$ e desvio padrão $$$\ sigma$ . De acordo com o Teorema do Limite Central, o valor médio observado será distribuído normalmente. Da lei dos grandes números, segue-se que sua média tenderá a $$$\ mu$ , e pelas propriedades da distribuição normal, segue-se que após $$$n$ medição, a variação observada da média diminuirá conforme $$$\ sigma / \ sqrt {n}$ . O desvio padrão pode ser considerado como o erro absoluto da medição média; neste caso, o erro relativo será igual a $$$\ delta = \ sigma / (\ sqrt {n} \ mu)$ . Estas são conclusões muito gerais, independentemente de suficientemente grandes $$$n$ da forma de distribuição específica da variável aleatória investigada. Duas regras úteis (não leis) se seguem:

1. Número mínimo de testes $$$n$ deve ser ditado pelo erro relativo desejado $$$\ delta$ . Além disso, se

$$

$$n \ geq \ left (\ frac {2 \ sigma} {\ mu \ delta} \ right) ^ 2,$$

então a probabilidade de que a média observada permaneça dentro do erro especificado será pelo menos $$$95 \%$ . At $$$\ mu$ próximo a zero, o erro relativo é melhor para substituir o absoluto.

2. Seja a hipótese nula de que a média observada é $$$\ mu$ . Então, se a média observada não ultrapassar $$$\ mu \ pm 2 \ sigma / \ sqrt {n}$ , então a probabilidade de que a hipótese nula seja verdadeira será pelo menos $$$95 \%$ .


Se substituído nessas regras $$$2 \ sigma$ em $$$3 \ sigma$ , o grau de confiança aumentará para $$$99,7 \%$ esta é uma regra muito forte $$$3 \ sigma$ , que nas ciências físicas separa suposições de fatos estabelecidos experimentalmente.

Será útil considerarmos a aplicação dessas regras à distribuição de Bernoulli, descrevendo uma variável aleatória que usa exatamente dois valores, condicionalmente chamados de "sucesso" e "falha", com uma dada probabilidade de sucesso. $$$p$ . Neste caso $$$\ mu = p$ e $$$\ sigma = \ sqrt {p (1-p)}$ , portanto, para o número necessário de experiências e o intervalo de confiança, obtemos

$$

$$n \ geq \ frac {4} {\ delta ^ 2} \ frac {1-p} {p} \ quad e \ quad np \ pm 2 \ sqrt {np (1-p)}.$$

A regra $$$2 \ sigma$ A distribuição de Bernoulli pode ser usada para determinar o intervalo de confiança ao plotar histogramas. Essencialmente, cada barra do histograma representa uma variável aleatória com dois valores: "acerto" - "falta", em que a probabilidade de acerto corresponde a uma função de probabilidade simulada. Como demonstração, geraremos muitas amostras para três distribuições: uniforme, geométrica e normal, após as quais comparamos as estimativas de dispersão dos dados observados com a dispersão observada. E aqui vemos novamente os ecos do teorema do limite central, manifestado no fato de que a distribuição de dados em torno dos valores médios nos histogramas está próxima do normal. No entanto, perto de zero, o spread se torna assimétrico e se aproxima de outra distribuição muito provável - exponencial. Este exemplo mostra bem o que eu quis dizer ao dizer que nas estatísticas estamos lidando com valores aleatórios dos parâmetros de uma variável aleatória.


Exemplo mostrando a proporção da estimativa de dispersão feita pela regra $$$2 \ sigma$ e o spread observado para três variáveis ​​aleatórias.

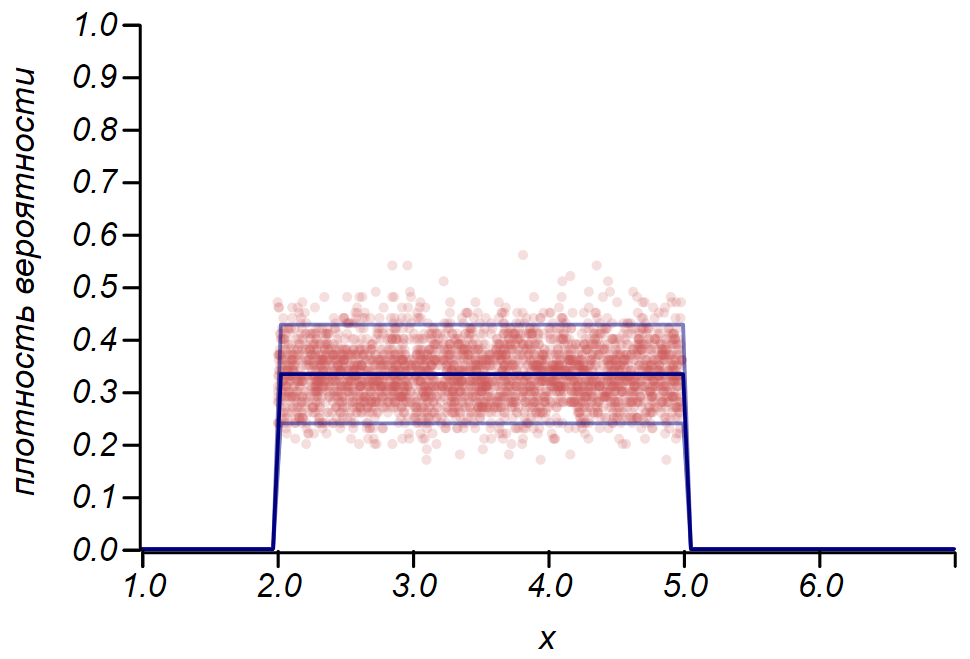
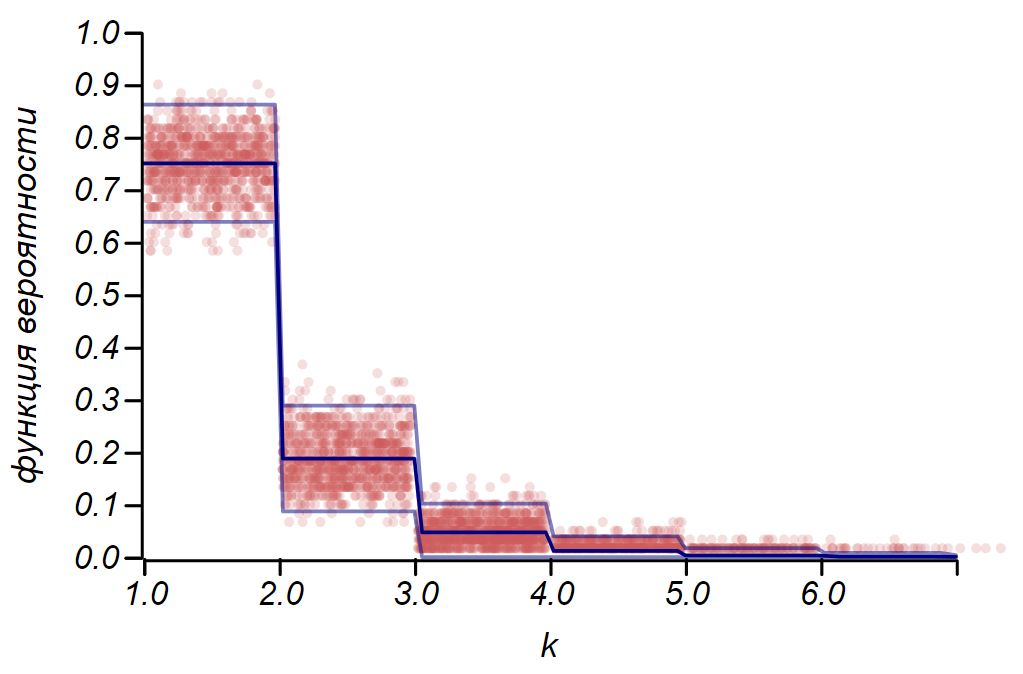
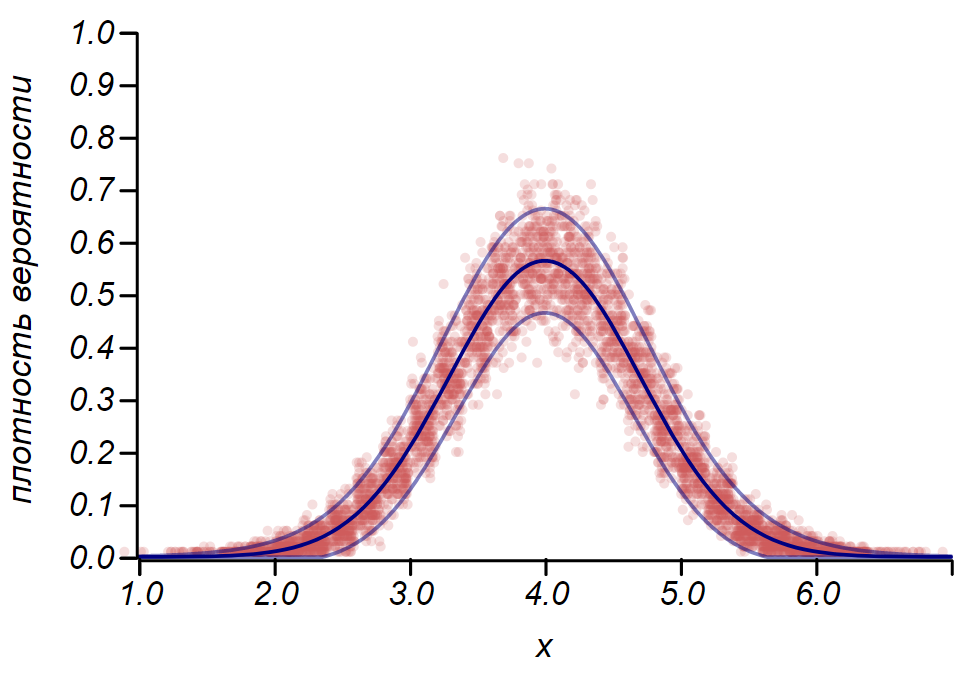
É importante entender que as regras $$$2 \ sigma$ e até $$$3 \ sigma$ não nos salve de erros. Eles não garantem a verdade de nenhuma afirmação, não são evidências. As estatísticas limitam o grau de desconfiança de uma hipótese e nada mais.

O matemático e autor de um excelente curso de teoria das probabilidades, Gian Carlo Rota, deu um exemplo em suas palestras no MIT. Imagine uma revista científica cujos editores tomaram uma decisão obstinada: aceitar para publicação exclusivamente artigos com resultados positivos que satisfaçam a regra $$$2 \ sigma$ ou mais rigoroso. Ao mesmo tempo, a coluna editorial indica que os leitores podem ter certeza de que, com probabilidade $$$95 \%$ o leitor não encontrará o resultado errado nas páginas desta revista! Infelizmente, essa afirmação pode ser facilmente refutada pelo mesmo raciocínio que nos levou a flagrante injustiça ao testar motoristas quanto ao álcool. Vamos $$$1000$ pesquisadores experientes $$$1000$ hipóteses, das quais apenas parte é verdadeira, digamos, $$$10 \%$ . Com base no significado do teste de hipóteses, podemos esperar que $$ hipóteses incorretas não serão erroneamente rejeitadas e serão registradas juntamente com $$ resultados verdadeiros. Total de $$$130$ Um bom terço estará errado!

Este exemplo demonstra perfeitamente nossa lei doméstica da maldade, que ainda não foi incluída na antologia da merfologia, a lei de Chernomyrdin :

Queríamos o melhor, mas acabou como sempre.

É fácil obter uma estimativa geral da porcentagem de resultados incorretos que serão incluídos nas edições da revista, assumindo que a parcela de hipóteses verdadeiras seja $$$0 <\ alpha <1$ e a probabilidade de aceitar uma hipótese errônea é $$$p$ :

$$

$$x = \ frac {(1- \ alpha) p} {\ alpha (1-p) + (1- \ alpha) p}.$$

As áreas que limitam o compartilhamento de resultados deliberadamente incorretos que podem ser publicados na revista são mostradas na figura.

Estimativa da porcentagem de publicações contendo resultados obviamente incorretos ao adotar vários critérios para testar hipóteses. Pode-se observar que aceitar hipóteses pela regra $$$2 \ sigma$ pode ser arriscado enquanto o critério $$$4 \ sigma$ já pode ser considerado muito forte.

Claro que não sabemos disso. $$$\ alpha$ , e nunca saberemos, mas certamente é menos do que a unidade, o que significa que, em qualquer caso, a declaração da coluna editorial não pode ser levada a sério. Você pode limitar-se a critérios rígidos $$$4 \ sigma$ mas requer um número muito grande de testes. Portanto, é necessário aumentar a parcela de hipóteses verdadeiras no conjunto de possíveis suposições. As abordagens padrão do método científico de cognição visam isso - a consistência lógica de hipóteses, sua consistência com fatos e teorias que provaram sua aplicabilidade, dependência de modelos matemáticos e pensamento crítico.

E novamente sobre o clima

No início do capítulo, conversamos sobre o fato de que fins de semana e mau tempo coincidem com mais frequência do que gostaríamos. Vamos tentar concluir este estudo. Cada dia chuvoso pode ser considerado como a observação de uma variável aleatória - o dia da semana obedecendo à distribuição de Bernoulli com probabilidade $$$1/7$ . Vamos assumir, como hipótese nula, a suposição de que todos os dias da semana são iguais em termos de clima e chuva, podendo chover em qualquer um deles igualmente provável. Como temos dois dias de folga, obtemos a probabilidade esperada de coincidência entre um dia ruim e um dia de folga igual $$ , esse valor será o parâmetro de distribuição de Bernoulli. Quantas vezes chove? Em diferentes épocas do ano, de maneiras diferentes, é claro, mas em Petropavlovsk-Kamchatsky, em média, há noventa dias de chuva ou neve em um ano. Portanto, o fluxo de dias com precipitação tem uma intensidade de cerca de $$$90/365 \ aproximadamente 1/4$ . Vamos calcular quantos fins de semana chuvosos devemos registrar para garantir que haja algum padrão. Os resultados são mostrados na tabela.

Período de observação	verão	ano	$$$5$ anos
Número esperado de observações	$$$23$	$$$90$	$$$456$
Número esperado de resultados positivos	$$$6$	$$$26$	$$$130$
Desvio significativo	$$$4$	$$$9$	$$$19$
Proporção significativa de maus número total de dias de folga	$$$42 \%$	$$$33 \%$	$$$29 \%$

Do que esses números estão falando? Se lhe parecer que, durante um ano consecutivo, não houve "verão", que o mal rock está perseguindo seu fim de semana enviando chuva a eles, isso pode ser verificado e confirmado. No entanto, durante o verão, rochas malignas só podem ser capturadas se mais de dois quintos de todos os fins de semana forem chuvosos. A hipótese nula sugere que apenas um quarto do fim de semana deve coincidir com o mau tempo. Em cinco anos de observação, já se pode esperar perceber desvios sutis que vão além $$$5 \%$ e, se necessário, continue com a explicação.

Aproveitei o diário meteorológico da escola, realizado de 2014 a 2018, e descobri o que aconteceu nesses cinco anos $$$459$ dias chuvosos deles $$$141$ caiu no fim de semana. Este é, de fato, mais do que o número esperado por $$$11$ dias, mas desvios significativos começam com $$$19$ dias, então isso, como dissemos na infância: "não conta". Aqui está uma série de dados e um histograma mostrando a distribuição do mau tempo por dia da semana. As linhas horizontais no histograma indicam o intervalo no qual um desvio aleatório da distribuição uniforme pode ser observado para a mesma quantidade de dados.


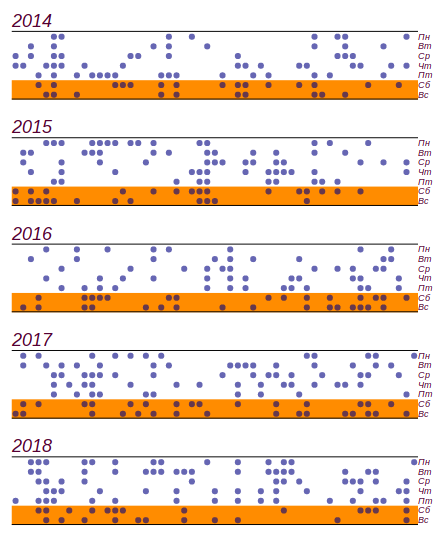
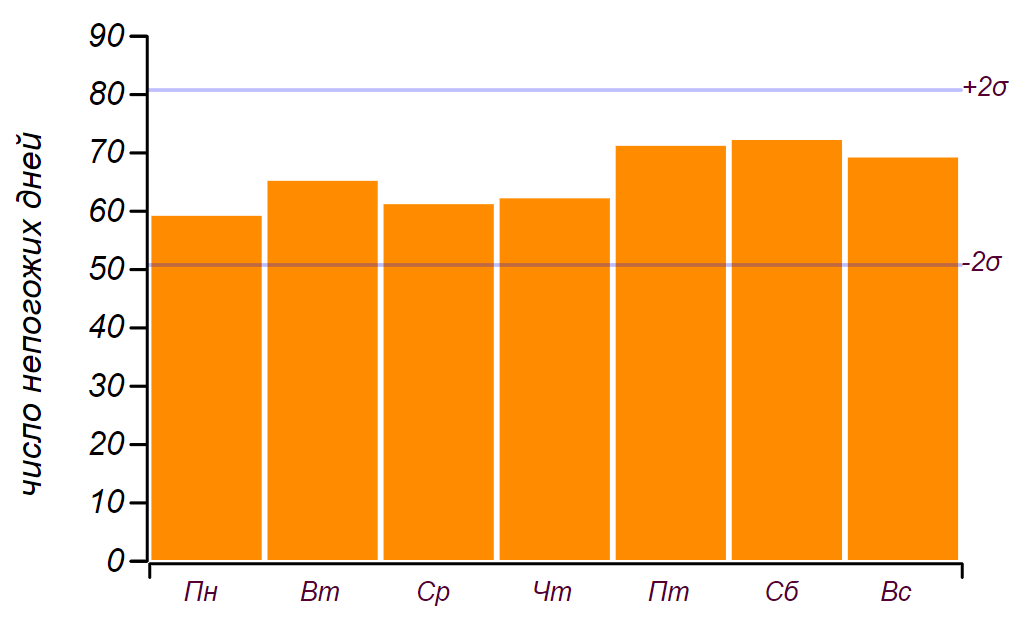A série inicial de dados e a distribuição de dias ruins por dias da semana obtiveram mais de cinco anos de observação.

Pode-se ver que desde sexta-feira, de fato, houve um aumento no número de dias com mau tempo. Mas os pré-requisitos não são suficientes para encontrar uma razão para esse crescimento: o mesmo resultado pode ser obtido simplesmente através da classificação por números aleatórios. Conclusão: durante cinco anos observando o clima, acumulei quase dois mil registros, mas não aprendi nada de novo sobre a distribuição do tempo pelos dias da semana.

Quando você olha para as anotações do diário, é evidente que o clima não vem sozinho, mas em períodos de dois a três dias ou mesmo em ciclones semanais. Isso afeta de alguma forma o resultado? Você pode tentar levar essa observação em consideração e assumir que chove em média por dois dias (de fato, $$$1,7$ dias), então a probabilidade de bloquear o final de semana aumenta para $$$3/7$ . Com essa probabilidade, o número esperado de partidas por cinco anos deve ser $$$195 \ pm21$ , ou seja, de $$$174$ antes $$$216$ vezes. Valor observado $$$141$ não se enquadra nessa faixa e, portanto, a hipótese do efeito de dois dias de mau tempo pode ser rejeitada com segurança. Aprendemos algo novo? Sim, nós aprendemos: parece que uma característica óbvia do processo não implica nenhum efeito. Vale a pena considerar, e faremos isso um pouco mais tarde. Mas a principal conclusão é que não há razões para considerar efeitos mais sutis, uma vez que as observações e, o mais importante, seu número, falam consistentemente em favor da explicação mais simples.

Mas o nosso descontentamento não é de cinco anos ou mesmo estatísticas anuais, a memória humana não é tão longa. É uma pena quando chove no fim de semana três ou quatro vezes seguidas! Com que frequência isso pode ser observado? Especialmente se você se lembrar que o clima desagradável não vem sozinho. A tarefa pode ser formulada da seguinte forma: “Qual é a probabilidade de que $$$n$ fim de semana consecutivo será chuvoso? " É razoável supor que o mau tempo forma um fluxo de Poisson com intensidade $$$1/4$ . Isso significa que, em média, um quarto dos dias de qualquer período será ruim. Observando apenas o fim de semana, não devemos alterar a intensidade do fluxo e, de todos os finais de semana, o mau tempo deve ser, em média, também um quarto. Assim, propomos a hipótese nula: a tempestade é Poisson, com um parâmetro conhecido, o que significa que os intervalos entre os eventos de Poisson são descritos por uma distribuição exponencial. Estamos interessados ​​em intervalos discretos: $$$0, \ 1, \ 2, \ 3$ dias, etc., portanto, podemos usar o analógico discreto da distribuição exponencial - a distribuição geométrica com o parâmetro $$$1/4$ . A figura mostra o que fizemos e pode ser visto que não é razoável rejeitar a suposição de que estamos observando o processo de Poisson.


A distribuição observada do comprimento das cadeias de fins de semana com falha e teórica. A linha fina mostra os desvios permitidos para o número de observações que temos.

Você pode se perguntar: quantos anos você precisa para fazer observações para que a diferença de $$$11$ dias poderiam ser confirmados ou rejeitados com confiança como um desvio aleatório? É fácil de calcular: probabilidade observada $$ diferente do esperado $$ em $$$0,02$ . Para registrar diferenças em centésimos, um erro absoluto não superior a $$$0,005$ isso faz $$$1,75 \%$ do tamanho medido. A partir daqui, obtemos o tamanho de amostra necessário $$$n \ geq (4 \ cdot 5/7) / (0,0175 ^ 2 \ cdot 2/7) \ aproximadamente 32000$ dias chuvosos. Vai demorar cerca de $$$4 \ cdot 32000/365 \ aprox 360$ anos de observações meteorológicas contínuas, porque apenas a cada quarto dia chove ou neva. Infelizmente, é mais do que o tempo em que Kamchatka faz parte da Rússia, então não tenho chance de descobrir como as coisas são "realmente". Especialmente se você levar em conta que, durante esse período, o clima conseguiu mudar drasticamente - a partir da Pequena Idade do Gelo, a natureza saiu no próximo ideal.

Então, como os pesquisadores australianos conseguiram registrar o desvio de temperatura em frações de grau e por que faz sentido considerar esse estudo? O fato é que eles usaram dados de temperatura por hora que não foram "reduzidos" por nenhum processo aleatório. Tão além $$$30$ anos de observações meteorológicas conseguiram acumular mais de um quarto de milhão de leituras, o que permite reduzir o desvio padrão da média $$$500$ tempos em relação ao desvio padrão diário da temperatura. Isso é suficiente para falar sobre precisão em décimos de grau. Além disso, os autores usaram outro método bonito que confirma a presença de um ciclo temporal: mistura aleatória das séries temporais. Essa mistura preserva propriedades estatísticas, como a intensidade do fluxo, no entanto, "apaga" os padrões temporais, tornando o processo verdadeiramente Poisson. A comparação de muitas séries sintéticas e experimentais permite verificar que os desvios observados do processo em relação a Poisson são significativos. Do mesmo modo, o sismólogo A. A. Gusev mostrou que os terremotos em qualquer região formam uma espécie de fluxo auto-semelhante com as propriedades de agrupamento. Isso significa que os terremotos tendem a se aglomerar no tempo, formando vedações de fluxo muito desagradáveis. Mais tarde, descobriu-se que a sequência de grandes erupções vulcânicas tem a mesma propriedade.

Outra fonte de aleatoriedade

Obviamente, o clima, como os terremotos, não pode ser descrito pelo processo de Poisson - esses são processos dinâmicos nos quais o estado atual é uma função dos anteriores. Por que nossas observações meteorológicas semanais favorecem um modelo estocástico simples? O fato é que exibimos o processo regular de formação de precipitação por um conjunto de sete dias, ou, falando a linguagem da matemática, em um sistema de deduções do módulo sete . Esse processo de projeção é capaz de gerar caos a partir de séries de dados bem ordenadas. A partir daqui, por exemplo, há uma aleatoriedade visível na sequência de dígitos da notação decimal da maioria dos números reais.

Já falamos sobre números racionais, aqueles expressos como frações inteiras. Eles têm uma estrutura interna, que é determinada por dois números: o numerador e o denominador. Porém, ao escrever em forma decimal, é possível observar saltos da regularidade na representação de números como $$$1/2 = 0,5 \ overline {0}$ ou $$$1/3 = 0. \ Overline {3}$ repetição periódica de seqüências já bastante aleatórias em números como $$$1/17 = 0. \ Overline {0588235294117647}$ . Os números irracionais não têm uma notação decimal finita ou periódica e, nesse caso, o caos reina com mais freqüência em uma sequência de números. Mas isso não significa que não haja ordem nesses números! Por exemplo, o primeiro número irracional encontrado por matemáticos $$$\ sqrt {2}$ em notação decimal gera um conjunto aleatório de números. No entanto, por outro lado, esse número pode ser representado como uma fração contínua infinita:

$$

$$\ sqrt {2} = 1 + \ frac {1} {2+ \ frac {1} {2+ \ frac {1} {2+ ...}}}.$$

É fácil mostrar que essa cadeia é realmente igual à raiz de dois, resolvendo a equação:

$$

$$x-1 = \ frac {1} {2+ (x-1)}.$$

As frações continuadas com coeficientes de repetição são gravadas em breve, como frações decimais periódicas, por exemplo: $$$\ sqrt {2} = [1, \ bar {2}]$ , $$$\ sqrt {3} = [1, \ overline {1,2}]$ . A famosa proporção áurea nesse sentido é o número irracional mais simples: $$$\ varphi = [1, \ bar {1}]$ . Todos os números racionais são representados na forma de frações contínuas finitas, algumas irracionais - na forma de infinitas, mas periódicas, são chamadas algébricas , as mesmas que não possuem uma notação finita mesmo nesta forma - transcendental . O mais famoso dos transcendentais é o número $$$\ pi$ , cria o caos tanto em decimal quanto na forma de uma fração contínua: $$$\ pi \ aproximadamente [3, 7,15,1,292,1,1,1,2,1,3,1,14,2,1, ...]$ . E aqui está o número de Euler $$$e$ o transcendental restante, na forma de uma fração contínua, exibe a estrutura interna oculta na notação decimal: $$$e \ approx [2,1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...]$ .

Provavelmente, nenhum matemático, começando com Pitágoras, suspeitou do mundo da astúcia, descobrindo o que é necessário, um número tão fundamental $$ p i é caótica estrutura complexa de modo subtil. Obviamente, pode ser representado como somas de séries numéricas bastante elegantes, mas essas séries não falam diretamente sobre a natureza desse número e não são universais. Acredito que os matemáticos do futuro descobrirão alguma nova representação de números, tão universais quanto frações contínuas, que revelarão a ordem estrita escondida pela natureza nos números.$\ pi$

$$

$$*\ *\ *$$

Os resultados deste capítulo são, na maioria das vezes, negativos. E, como autor que quer surpreender o leitor com padrões ocultos e descobertas inesperadas, duvidei que devesse ser incluído no livro. Mas nossa conversa sobre o clima entrou em um tópico muito importante - o valor e o significado da abordagem das ciências naturais.

Uma garota sábia, Sonya Shatalova, olhando o mundo através do prisma do autismo, aos dez anos de idade, deu uma definição muito concisa e precisa: "A ciência é um sistema de conhecimento baseado na dúvida". O mundo real é instável e se esforça para se esconder atrás da complexidade, aleatoriedade visível e falta de confiabilidade das medições. A dúvida nas ciências naturais é inevitável. A matemática parece ser um domínio de certeza, no qual, ao que parece, podemos esquecer a dúvida. E é muito tentador se esconder atrás dos muros deste reino; considere, em vez dos modelos mundiais irreconhecíveis, que podem ser completamente investigados; conte e calcule, o benefício da fórmula está pronto para digerir qualquer coisa. Mas, no entanto, a matemática é uma ciência e a dúvida é uma profunda honestidade interna que não dá descanso até que a construção matemática seja eliminada de suposições adicionais e hipóteses desnecessárias. No domínio da matemática, eles falam uma linguagem complexa, mas harmoniosa, adequada para raciocinar sobre o mundo real. É muito importante se familiarizar com esse idioma,a fim de impedir que os números representem estatísticas, não permitir que os fatos pretendam ser conhecimento, e a ignorância e a manipulação contrastem a ciência real.