A matemática em Gamedev é simples. Unidade de curvas e ondulações para efeito de chuva

Olá pessoal! Meu nome é Grisha e sou o fundador da CGDevs. Vamos continuar falando sobre matemática ou algo assim. Talvez a principal aplicação da matemática no desenvolvimento de jogos e na computação gráfica em geral seja o VFX. Então, vamos falar sobre um desses efeitos - chuva, ou melhor, sobre sua parte principal, que requer matemática - ondulações na superfície. Escreva sucessivamente um shader para ondulações na superfície e analise sua matemática. Se estiver interessado - bem-vindo ao gato. Projeto Github anexado.



Às vezes, chega um momento na vida em que um programador precisa pegar um pandeiro e pedir chuva. Em geral, o tópico da modelagem de chuva em si é muito profundo. Existem muitos trabalhos matemáticos em diferentes partes desse processo, desde a queda de gotas e os efeitos associados a ela até a distribuição de gotas em volume. Analisaremos apenas um aspecto - o shader, que nos permitirá criar um efeito semelhante à onda a partir de uma queda. É hora de pegar um pandeiro!


Onda matemática

Ao pesquisar na Internet, você encontra muitas expressões matemáticas engraçadas para gerar ondulações. Freqüentemente, eles consistem em algum tipo de números "mágicos" e funções periódicas sem justificativa. Mas, em geral, a matemática desse efeito é bastante simples.

Precisamos apenas de uma equação de onda plana no caso unidimensional. Por que analisaremos plana e unidimensional um pouco mais tarde.

A equação da onda plana no nosso caso pode ser escrita como:

Resultado = A * cos (2 * PI * (x / comprimento da onda - t * frequência));
Onde:
Aresult - amplitude no ponto x, no tempo t
A é a amplitude máxima
comprimento de onda - comprimento de onda
frequência - frequência das ondas
PI - número PI = 3,14159 (flutuante)

Shader


Vamos brincar com os shaders. Para o "top" será responsável pela coordenada -Z. Isso é mais conveniente no caso 2D do Unity. Se desejado, o shader não será difícil de reescrever para Y.

A primeira coisa que precisamos é da equação de um círculo. A onda do nosso shader será simétrica em relação ao centro. A equação do círculo no caso 2d é descrita como:

r ^ 2 = x ^ 2 + y ^ 2

precisamos de um raio, então a equação assume a forma:

r = sqrt (x ^ 2 + y ^ 2)

e isso nos dará simetria sobre o ponto (0, 0) na malha, o que reduzirá tudo ao caso unidimensional de uma onda plana.

Agora vamos escrever um shader. Não analisarei todas as etapas da escrita de um sombreador, pois esse não é o objetivo do artigo, mas a base é retirada do Shader de superfície padrão do Unity, cujo modelo pode ser obtido através de Create-> Shader-> StandardSurfaceShader.

Além disso, as propriedades necessárias para a equação da onda são adicionadas : _Frequency , _WaveLength e _WaveHeight . Propriedade _Timer (seria possível usar o tempo com a gpu, mas durante o desenvolvimento e a animação subsequente, é mais conveniente controlá-la manualmente.

Escrevemos a função getHeight para obter a altura (agora essa é a coordenada Z) substituindo a equação do círculo na equação da onda

Ao escrever um sombreador com nossa equação de onda e a equação de círculo, obtemos esse efeito.



Há ondas. Mas quero que a animação comece e termine com um avião. A função seno nos ajudará com isso. Multiplicando a amplitude pelo pecado (_Timer * PI), obtemos uma aparência suave e o desaparecimento das ondas. Como _Timer usa valores de 0 a 1 e o seno em zero e no PI é zero, é exatamente isso que você precisa.


Embora não seja como uma gota caindo. O problema é que a energia das ondas é perdida uniformemente. Adicione a propriedade _Radius, que será responsável pelo raio do efeito. E multiplicamos a amplitude da pinça (_Radius - rad, 0, 1) e obtemos um efeito mais parecido com a verdade.


Bem, o passo final. O fato de a amplitude em cada ponto individual atingir seu máximo em um tempo igual a 0,5 não é totalmente verdadeiro, é melhor substituir essa função.



Então fiquei com preguiça de contar, e apenas multipliquei o seno por (1 - _Timer) e consegui essa curva.



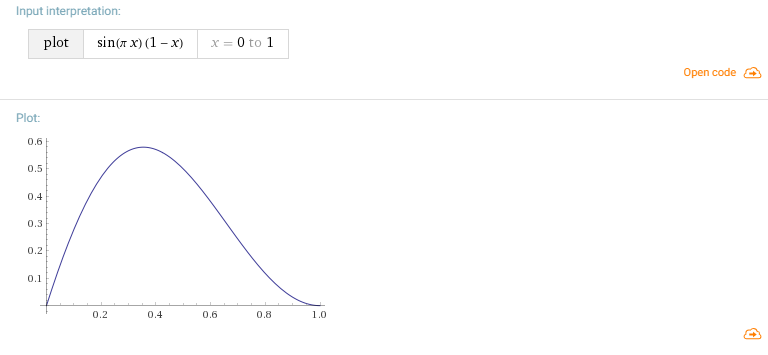
Mas, em geral, do ponto de vista da matemática, também é possível selecionar a curva desejada com base na lógica em que momento você deseja um pico e uma forma aproximada e, em seguida, criar interpolação nesses pontos.

O resultado é um sombreador e efeito.




Malha de malha é importante

Voltando um pouco ao tópico do artigo anterior . As ondas são implementadas pelo shader de vértice, de modo que a malha da malha desempenha um papel bastante grande. Como a natureza do movimento é conhecida, a tarefa é simplificada, mas, em geral, o visual final depende da forma da grade. A diferença se torna insignificante com alta poligonalidade, mas, quanto ao desempenho, quanto menos polígonos, melhor. Abaixo estão as figuras que ilustram a diferença entre grades e imagens.

Corretamente: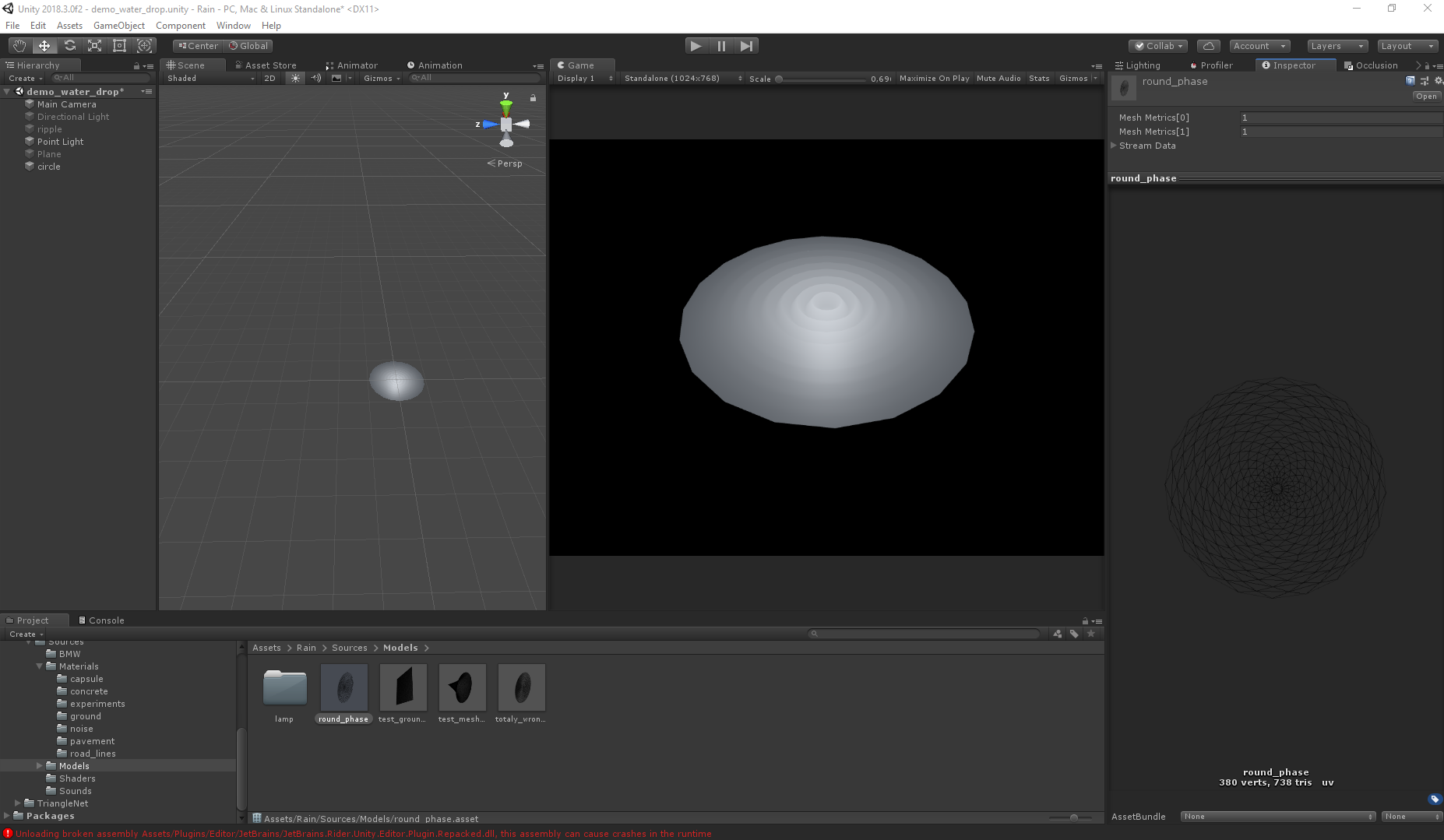



Errado: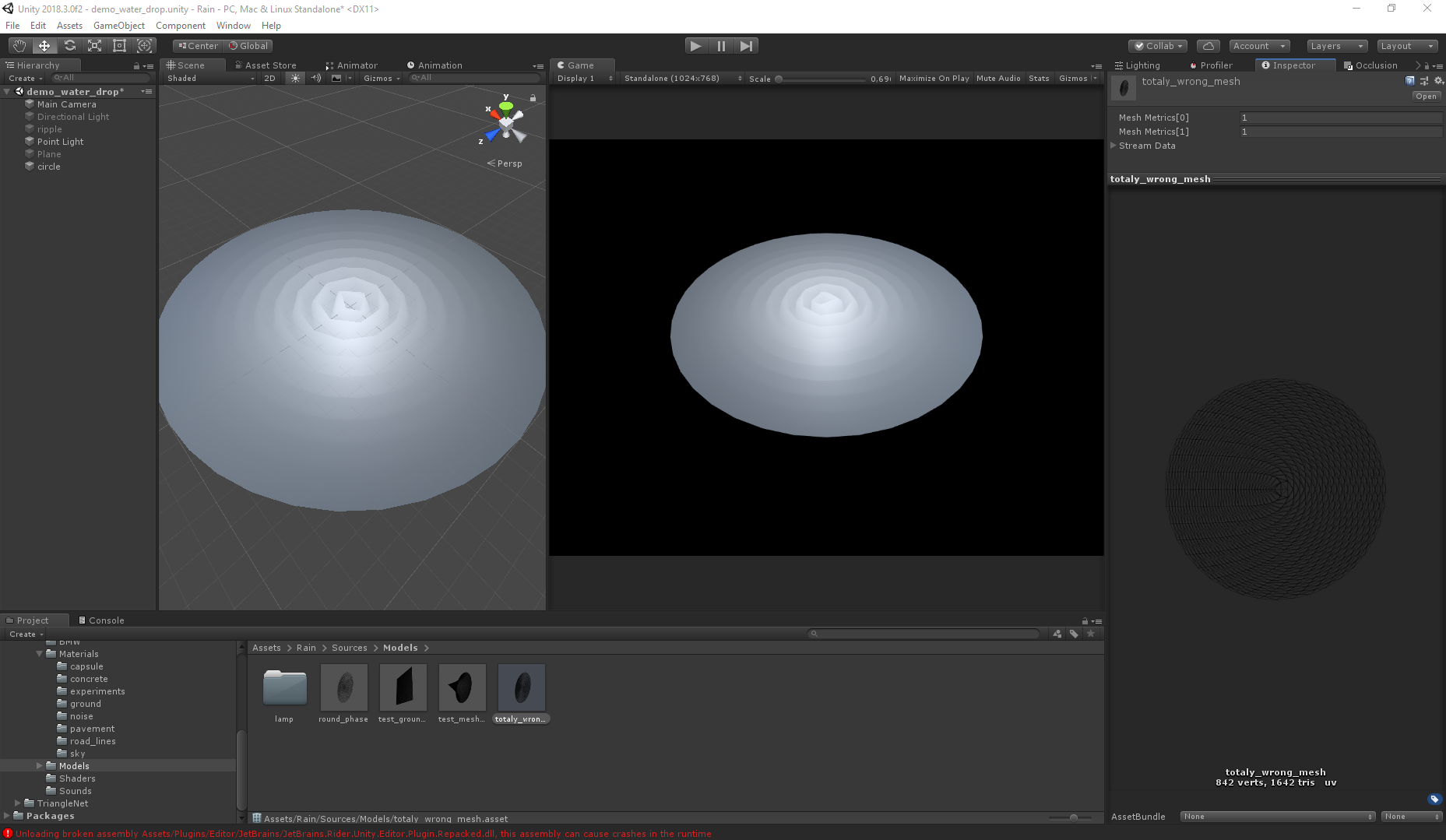



Mesmo com o dobro do número de polígonos, a segunda malha fornece o visual errado (as duas malhas são geradas usando o Triangle.Net, apenas usando algoritmos diferentes).

Visual final


Em uma versão diferente do shader, uma parte especial foi adicionada para criar ondas não estritamente no centro, mas em vários pontos. Como isso é implementado e como você pode passar esses parâmetros, posso dizer nos seguintes artigos, se o tópico é interessante.

Aqui está o próprio shader:


O projeto como um todo e como funciona pode ser encontrado aqui . É verdade que parte dos recursos teve que ser removida devido a limitações de peso do github (hdr skybox e carro).

Obrigado pela atenção! Espero que o artigo seja útil para alguém, e ficou um pouco mais claro por que a trigonometria, a geometria analítica (tudo relacionado às curvas) e outras disciplinas matemáticas podem ser necessárias.