Sumário
É fornecida uma descrição das leis estabelecidas em uma lista seqüencial de todas as soluções para o problema de distribuição do n-Queens. Está estabelecido que:
- A proporção de soluções completas na lista geral de todas as soluções diminui, com o aumento do valor de n.
- As soluções completas são distribuídas em uma lista seqüencial de todas as soluções, de forma que as soluções completas localizadas próximas umas das outras na lista provavelmente sejam encontradas.
- Há simetria na ordem das soluções completas na lista geral de todas as soluções. Se na i-ésima posição desde o início da lista a solução estiver concluída, a solução simétrica do final da lista localizada na posição n-i + 1 também estará completa (a regra de simetria das soluções).
- Quaisquer pares de soluções, curtos e completos, localizados simetricamente na lista de todas as soluções, são complementares - a soma dos índices de posição das linhas correspondentes é constante e igual a n + 1 (regra de complementaridade de soluções). Isso sugere que apenas a primeira metade da lista de todas as soluções completas é "única"; qualquer solução completa da segunda metade da lista pode ser obtida com base na regra de complementaridade. Uma conseqüência dessa regra é o fato de que, para qualquer valor de n, o número de soluções completas sempre será um número par.
- A atividade das células das linhas da matriz da solução é simétrica em relação ao eixo horizontal que passa pelo meio desta matriz. Isso significa que a atividade das células da i-ésima linha sempre coincide com a atividade das células da linha n-i + 1. Por atividade, entende-se a frequência com que o índice de células ocorre na linha correspondente da lista de soluções completas. Da mesma forma, a atividade das células das colunas da matriz da solução é simétrica em relação ao eixo vertical, dividindo a matriz em duas partes iguais
- Independentemente de n, em uma pesquisa seqüencial de todas as soluções, a primeira solução completa aparece somente após uma determinada sequência de soluções curtas. O tamanho da sequência inicial de soluções curtas aumenta com n. O comprimento da lista de soluções curtas antes do aparecimento da primeira solução completa para valores pares de n é significativamente maior que para os valores ímpares mais próximos.
- A linha na matriz de decisão, na qual as dificuldades começam a avançar e a primeira decisão curta é formada, divide a matriz de acordo com a regra da proporção áurea. Para pequenos valores de n, essa conclusão é aproximada, no entanto, com um aumento no valor de n, a precisão de tal conclusão aumenta assintoticamente para o nível da regra padrão.
Esta publicação apresenta os principais resultados do artigo [1] , publicado na revista “Modeling of Artificial Intelligence, 2018, 5 (1)”. Em Habré, havia trabalhos relacionados a um problema do n-Queens: [2] , [3] ,
O problema de distribuir n rainhas em um tabuleiro do tamanho de um nxn tem uma longa história. Foi originalmente formulado em 1848 por M. Bezzel [4] como uma tarefa intelectual para um tabuleiro de xadrez regular. Com o tempo, a afirmação do problema foi ampliada por F. Nauck [5], e o tamanho de um tabuleiro de xadrez pode assumir qualquer valor.
1. Introdução
A afirmação do problema é bastante simples: você precisa distribuir n rainhas em um tabuleiro de xadrez de tamanho nxn, de modo que em cada linha, cada coluna e também nas diagonais esquerda e direita passando pela célula onde a rainha está localizada, não haja mais do que uma rainha. Essa tarefa é fácil de entender ou explicar para alguém, mas é bastante difícil resolvê-la. O fato é que não existem regras com base nas quais você pode organizar rainhas em cada linha para obter uma solução. Uma solução só pode ser obtida enumerando várias variantes da disposição das rainhas em determinadas linhas. No entanto, a complexidade desse método de solução reside no fato de que o número de todas as variantes do arranjo de rainhas aumenta exponencialmente com o aumento de n. Além disso, dar um passo à frente para colocar a rainha na posição livre de uma determinada linha leva a uma alteração na lista de posições livres nas linhas restantes e, ao retornar um passo para formar um ramo de busca, é necessário limpar os traços de ações executadas anteriormente.
Há um grande número de publicações relacionadas a vários aspectos da solução do problema do n-Queens. Eles podem ser atribuídos a várias áreas de pesquisa: a busca de todas as soluções completas para um determinado valor do tamanho de um tabuleiro de xadrez (n), o desenvolvimento de um algoritmo rápido para encontrar uma solução para diferentes valores de n, a solução do problema completo para uma solução completa, para uma composição arbitrária de k rainhas, perguntas a complexidade computacional dos cálculos algorítmicos, bem como várias modificações da formulação original do problema. Para me familiarizar com essas áreas, eu recomendaria publicações interessantes de B. Jordan, S. Brett [6] e IP Gent, C. Jefferson, P. Nightingale [7], que fornecem uma visão geral bastante detalhada de várias áreas de pesquisa. Destaca-se a publicação na Internet [8], apoiada por Walter Costers, que foi preparada por um grupo da Universiteit Leiden e contém links para 342 publicações relacionadas ao problema das n-rainhas (em dezembro de 2018).
Embora o problema do n-Queens permaneça ativo por mais de 150 anos e um grande número de publicações tenha aparecido durante esse período, não consegui encontrar um emprego que fosse relevante para a busca de padrões nos resultados da solução desse problema. A maioria dos projetos relacionados à busca de todas as soluções provavelmente não salvou as soluções encontradas e não viu o que estava “dentro”. Ali, na declaração do problema, havia outros objetivos dominantes, e nossos estimados colegas os alcançaram. No entanto, remotamente, pareceu-me que a situação é semelhante a quando uma pessoa cozinha ovos no café da manhã, mas não os come, mas os joga fora, deixando apenas o número de ovos cozidos em sua memória. Sempre tive certeza de que, se os dados não forem aleatórios, deve haver uma certa regularidade neles, mesmo que não possamos encontrar essa regularidade. Foi essa convicção que foi o motivo da busca de padrões nessa tarefa.
Juntamente com o desejo de fornecer aos membros da comunidade Habr informações úteis para reflexão, eu gostaria que programadores talentosos, a maioria deles no Habr, prestassem mais atenção a uma direção de desenvolvimento como a simulação por computador (Simulação Computacional). Como método de pesquisa, essa "Matemática Algorítmica" é usada na "vanguarda" de muitas áreas: Inteligência Artificial, Ciência de Software, Ciência de Dados, ... e tenho certeza de que problemas muito complexos e importantes para aplicação prática serão resolvidos com base na matemática algorítmica caso contrário.
Definições
A seguir, indicaremos o tamanho do tabuleiro de xadrez pelo símbolo n. Uma solução será chamada completa se todas as n rainhas forem consistentemente colocadas em um tabuleiro de xadrez. Todas as outras soluções, quando o número de rainhas colocadas corretamente for menor que n - chamaremos soluções curtas. Pelo comprimento de uma solução, queremos dizer o número (k) de rainhas corretamente colocadas. O número de todas as soluções, para um determinado valor de n, será indicado por m. Como análogo de um "tabuleiro de xadrez" de tamanho nx n., Consideraremos uma "matriz de solução" de tamanho nx n.
Iniciar
Para realizar um estudo, um algoritmo foi desenvolvido para procurar todas as soluções para um valor arbitrário de n. Não usamos recursão padrão ou o sistema usual de loops aninhados. Para grandes valores de n, essa abordagem seria bastante problemática. O algoritmo foi construído com base em um conjunto de eventos em interação, em cada um dos quais um determinado sistema de ações está ocorrendo, interconectado. Isso possibilita simplesmente implementar o mecanismo para alterar o espaço de estado ao escolher o próximo nó na ramificação da solução do problema (rastreamento avançado) ou limpar os rastreamentos de ações executadas anteriormente, ao retornar a uma ou mais etapas (rastreamento posterior). Não há requisitos especiais para o tamanho da memória ou a velocidade do processador no algoritmo.
Com base nesse algoritmo, foram encontradas todas as soluções seqüenciais (curtas e completas) para vários valores da matriz da solução n = (7, ..., 16). Como o tamanho da lista de soluções completas é a sequência nomeada A Enciclopédia On-line de Sequências Inteiras (sequência A000170 [9]) e é indicada em várias publicações, parece-me interessante listar o tamanho da lista de todas as soluções (curta + completa) para os valores de n considerados por nós: 7 (194), 8 (736), 9 (2 936), 10 (12 774), 11 (61 076), 12 (314 730), 13 (1 716 652), 14 (10 030 692), 15 ( 62 518 772), 16 (415 515 376).
Além disso, usando as soluções encontradas, fornecemos a redação de alguns problemas, métodos para resolvê-los e uma descrição dos resultados.
1. O espaço de estado no qual as soluções são pesquisadas
A enumeração de várias opções para a organização de rainhas em determinadas linhas de uma matriz de uma decisão de tamanho n leva à formação de um espaço de estados. Se não houvesse proibições no arranjo de rainhas em uma ou outra célula da matriz, o tamanho do espaço de estado seria n n . Se levarmos em conta apenas a regra que proíbe a localização de mais de uma rainha em cada linha e cada coluna, obteremos um subconjunto do espaço de estado cujo tamanho será n! Esse subconjunto do espaço de estados corresponde ao problema da distribuição de n pela torre. Se, junto com isso, também levarmos em conta a regra que proíbe a localização de mais de uma rainha nas diagonais esquerda e direita que passam pela célula onde a rainha está localizada, obteremos algum espaço de pesquisa cujo tamanho será menor que n! ... Chamamos esse subconjunto de espaço de estado - um espaço de pesquisa produtivo, baseado no fato de que somente neste subespaço são todas as soluções possíveis. Quaisquer ramificações concluídas no espaço produtivo de pesquisa são soluções com um certo número de rainhas colocadas corretamente. Basicamente, essas são decisões curtas e apenas uma pequena parte restante são decisões completas.
A Figura 1 mostra gráficos do logaritmo natural de três indicadores: a) o valor fatorial (n!) Sobre o tamanho da matriz de decisão; b) o número de todas as decisões (curtas e completas); c) o número de soluções completas, dependendo do tamanho da matriz da solução (n). Como esperado, todas as curvas são caracterizadas por um aumento exponencial com o aumento de n. As taxas de crescimento do número de todas as soluções e do número de soluções completas diferem, embora isso não seja tão perceptível no gráfico, devido ao pequeno tamanho da amostra de n valores. Por exemplo, para n = 13, a diferença entre os logaritmos desses indicadores é 3,148, e para n = 16 essa diferença aumenta em 0,190 e é 3,338. Obviamente, com um aumento adicional de n, essa discrepância será mais significativa.

Fig. 1 Dependência do logaritmo do tamanho do espaço de estados no valor n
2. Como a proporção de decisões completas na lista geral de todas as decisões muda?
Obviamente, se a taxa de crescimento do número de soluções completas ficar atrás da taxa de crescimento do número de todas as soluções, a probabilidade de encontrar uma solução completa na lista geral de todas as soluções diminuirá com o aumento do valor de n. A Figura 2 mostra um gráfico da proporção de soluções completas na lista geral de todas as soluções sobre o valor de n. Observa-se que, com um aumento no tamanho da matriz da solução, a participação de todas as soluções completas na lista geral diminui. Para os valores iniciais n = (7, ..., 14), esse valor diminui 5,66 vezes do valor 0,2062 a 0,0364 e, em seguida, uma diminuição gradual e assintótica desse valor continua. Aqui surge uma contradição formal entre as duas afirmações: por um lado, o número de soluções completas aumenta exponencialmente com o aumento de n; por outro, a probabilidade de obter uma solução completa em uma lista seqüencial de todas as soluções diminui constantemente. Esse aparente paradoxo é explicado com muita simplicidade, o tamanho do espaço produtivo e o tamanho associado da lista de todas as soluções cresce mais rapidamente com o aumento de n do que o número de soluções completas. É como tentar encontrar uma agulha no palheiro - a quantidade de feno "com o aumento de n" cresce mais rápido que o número de agulhas perdidas ali. Portanto, podemos supor que se para n = 27, o número de soluções completas for aproximadamente 2,346 * 10 17 , o valor correspondente do número de todas as soluções provavelmente será de 3-4 ordens de magnitude maiores que ~ 10 20
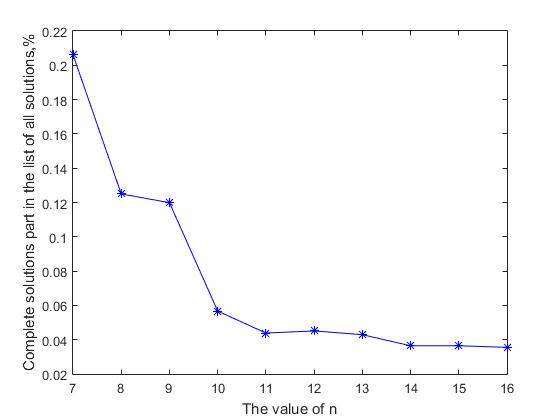
Fig. 2 Diminuição da proporção de soluções completas na lista geral de todas as soluções com o aumento de n
3. Qual é a frequência de soluções de vários comprimentos na lista de todas as soluções?
Como mencionado anteriormente, todas as ramificações concluídas no espaço produtivo de pesquisa são soluções com um número diferente de rainhas colocadas corretamente.
É interessante para nós com que frequência existem soluções de vários comprimentos na lista geral de todas as soluções.
A Tabela 1 para os valores n = (7, ..., 12) apresenta os valores correspondentes das frequências relativas para soluções com comprimentos diferentes. A representação visual correspondente desses dados é mostrada na Figura 3.
A análise da tabela nos permite tirar as seguintes conclusões:
a) para cada matriz de tamanho n, existe um certo comprimento da solução que possui uma frequência máxima (destacada em negrito).
Tabela 1. Frequência relativa (%) de soluções de diferentes comprimentos (k) para uma matriz de tamanho n = (7, ..., 12)
| n \ k | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|
| 7 | 10,31 | 31,23 | 27,84 | 20,62 | | | | | |
| 8 | 2,45 | 20,38 | 34,78 | 29,89 | 12,50 | | | | |
| 9 | 0,34 | 5,79 | 21,73 | 35,83 | 34,32 | 11,99 | | | |
| 10 | 0,05 | 1,35 | 8.41 | 25,62 | 32,94 | 25,96 | 5,67 | | |
| 11 | | 0,15 | 2.12 | 11,80 | 26,71 | 34,47 | 20,36 | 4,39 | |
| 12 | | 0,01 | 0,29 | 3,28 | 13,56 | 29,88 | 31,29 | 17.18 | 4.51 |
b) à medida que n aumenta, aumenta o número de soluções com comprimentos diferentes. Consequentemente, a frequência relativa de todas as decisões diminui.
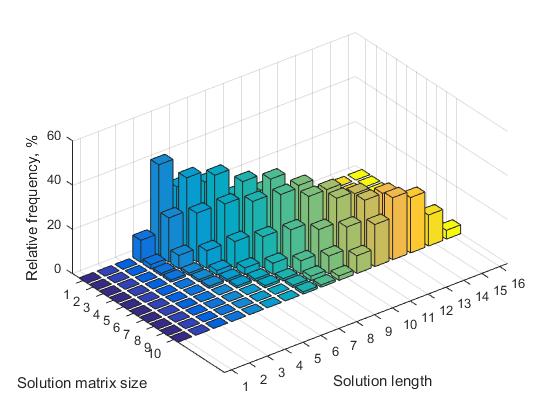
Fig. 3 Frequência de soluções de vários comprimentos, dependendo do tamanho da matriz da solução, n = 7, ..., 16
c) para cada matriz de tamanho n, existe um certo tamanho mínimo do comprimento da solução, abaixo do qual soluções curtas não ocorrem. Com o aumento de n, o valor desse limite aumenta. Por exemplo, para n = 8, o valor limite é 4, respectivamente, para n = 16, o valor limite é 7.
4. Qual é o arranjo relativo de soluções completas em uma lista seqüencial de todas as soluções?
Na declaração do problema "sobre a distribuição de n rainhas", não há razões que justifiquem a sequência de decisões completas na lista geral de todas as soluções. Estávamos interessados em saber se as soluções completas da lista geral são distribuídas uniformemente, aleatoriamente ou se possuem algumas peculiaridades. Para descobrir, analisamos as distâncias entre as soluções completas mais próximas em uma lista seqüencial de todas as soluções. Como pode ser visto na Figura 4, onde para n = 12, é apresentado um gráfico de mudanças nas frequências correspondentes,
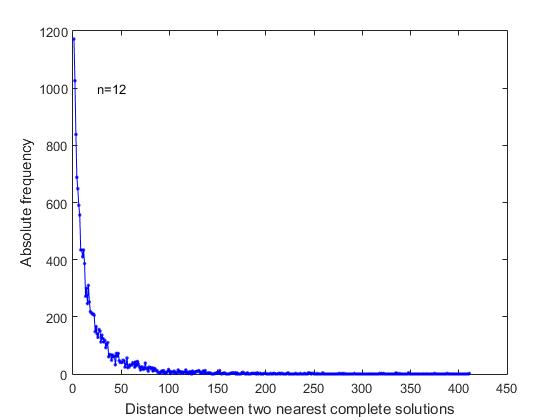
Fig. 4 Frequência versus distância entre as soluções completas mais próximas em uma lista seqüencial de todas as soluções completas (n = 12)
com a maior frequência, existem soluções completas que se seguem imediatamente em uma lista seqüencial comum de todas as soluções. É o caso da formação do ramo de pesquisa quando o relacionamento de posições livres nas últimas linhas permite formar duas ou mais soluções completas consecutivas. Além disso, a frequência máxima são aquelas soluções completas entre as quais estão localizadas: uma solução curta, duas soluções curtas, etc.
5. Existe um padrão no arranjo de soluções completas na lista geral de todas as soluções?
Para responder a essa pergunta, analisamos listas seqüenciais de todas as soluções para os valores n = (7, ..., 16). Para demonstrar claramente os resultados, na Figura 5, para o valor n = 8, é apresentado um gráfico em que o comprimento de cada solução na lista de todas as 736 soluções é indicado sucessivamente. Aqui, apenas 92 soluções estão completas e destacadas em vermelho, as 644 restantes são curtas e destacadas em azul. Pode-se observar que as soluções completas não são distribuídas igualmente na lista de todas as soluções. Há áreas em que soluções completas são mais comuns e há lugares em que soluções completas são raras ou nem um pouco.

Fig. 5 O comprimento de cada solução em uma lista seqüencial de todas as soluções, para uma matriz 8 x 8 (soluções em vermelho total, soluções em azul curto). O número total de todas as soluções é 736
No entanto, algo mais é importante aqui. Se você observar atentamente a figura semelhante a um código de barras azul-vermelho, perceberá um recurso muito importante: todas as linhas vermelhas são simétricas em relação a alguma linha vertical condicional que passa pelo meio da lista de soluções. , , i- , , m-i+1. , n=8, , 43- , , 736- 43 +1=694. 17- 10x10 368- , 12774-17+1=12407. . . n, , i- , , m-i+1 ( ). m, , . , n, , . ( – ).
, – . n+1 . , 17- n=10 368- (1, 5, 7, 10, 4, 2, 9, 3, 6, 8).
, 12407 (10, 6, 4, 1, 7, 9, 2, 8, 5, 3). , (11, 11, …,11). n, , , . . n, ( , ), , – n+1 ( ). Q(i ) Q1(i) – ,
<b>`Q ( i ) + Q1 ( i ) = n + 1, i = (1, n) `</b>
Essa regra significa que, se uma solução completa for obtida na i- ésima etapa, a solução completa simétrica na etapa m - i +1 se tornará conhecida . Portanto, ao procurar todas as soluções completas, basta encontrar apenas a primeira metade de todas as soluções completas. A segunda metade da lista de soluções completas pode ser determinada a partir das soluções já obtidas, com base na regra da complementaridade. O critério para alcançar metade da lista de soluções completas é o cumprimento da regra de complementaridade entre a solução completa anterior Q (i-1) e a subsequente Q (i) . ou seja, é necessário que a soma de cada par de índices correspondentes de duas soluções consecutivas seja igual a n + 1 . Como qualquer solução completa da lista de todas as soluções completas é única, apenas as soluções completas consecutivas serão complementares nos dois lados da borda que divide a lista pela metade.
Essas duas regras permitirão no futuro, ao procurar todas as soluções completas para qualquer próximo valor de n, reduzir a quantidade de computação e, consequentemente, o tempo de cálculo pela metade.
6. Visualização da sequência de etapas para encontrar a primeira solução completa
Como é o processo de executar as etapas adiante (rastreamento avançado) e retornando (rastreamento posterior) ao formar um ramo de uma pesquisa de solução? Para responder a essa pergunta, determinamos, para uma matriz 10 x 10, a sequência das 194 transições iniciais entre as linhas até que a primeira solução completa apareça. O gráfico correspondente é mostrado na Figura 6. Linhas azuis indicam um movimento para frente e linhas vermelhas indicam um retorno. Durante essas 194 etapas, foram criadas 35 soluções curtas. A figura mostra que a maioria das transições (84,5%) ocorre nas entrelinhas (5, 6, 7, 8). Este é um tipo de "gargalo" no caminho para o "objetivo". Como se segue na figura, existem apenas 7 casos de mudança para a quarta linha e um caso de mudança para a terceira linha. Há também 13 casos de mudança para a 9ª linha. Três tentativas de passar para a 10ª linha não tiveram êxito, pois não havia posição vazia nesses ramos de pesquisa na 10ª linha. Este exemplo demonstra todas as ramificações de

Fig. 6 Visualização dos eventos Backtracking (vermelho) e Forwardtracking (azul) para as primeiras 194 etapas de pesquisa (n = 10)
soluções, até a primeira solução completa. Qualquer algoritmo para resolver um problema desse tipo será eficaz se contiver um mecanismo que elimine todos (ou parte) dos ramos que levam a soluções curtas.
7. Após quantas decisões curtas a primeira solução completa aparece?
Considerando que as soluções completas aparecem de maneira diferente em diferentes partes da lista de todas as soluções, parece importante descobrir em quantas soluções curtas a primeira solução completa aparece ao pesquisar todas as soluções de maneira seqüencial. Para este propósito, para os valores n = (7, ..., 35), todas as soluções curtas foram calculadas sucessivamente até o aparecimento da primeira solução completa. Como pode ser visto na Figura 7, que mostra um gráfico da dependência de n, o logaritmo natural do número da etapa, quando a primeira solução completa apareceu, para valores pares de n, a primeira solução completa aparece muito mais tarde que para os valores ímpares mais próximos de n. Por exemplo, para um valor ímpar n = 21, a primeira solução completa aparece na etapa 3138 e para o próximo valor par n = 22, a primeira solução completa aparece na etapa 628169. Por conseguinte, para o próximo valor ímpar n = 23, a primeira solução completa aparece na etapa 9155.

Fig. 7 O número de soluções curtas até a primeira solução completa, para vários valores de n
O número de etapas de iteração para o par n = 22 é 200,2 e 68,6 vezes mais, respectivamente, que os valores ímpares mais próximos. Isto é especialmente evidente na contagem do tempo para n = 34. Aqui, a primeira solução completa aparece nas etapas 826 337 184 e nos números ímpares mais próximos (33, 35), respectivamente, nas etapas 50 704 900th e 84 888 759th. Também deve ser dito sobre a violação do crescimento monotônico do número de soluções curtas antes do surgimento da primeira solução completa, com o aumento de n. Para valores pares de n, isso ocorre em n = 19, para valores ímpares, em n = 24 en = 26.
8. A frequência de células de cada linha na lista de todas as soluções completas é a mesma?
A matriz de decisão do tamanho nxn, que serve como análogo de um tabuleiro de xadrez, é como uma cena na qual todos os eventos ocorrem. Qualquer solução completa formada nesta cena consiste em índices de células de linhas diferentes, porque cada célula é um nó no ramo de pesquisa da solução. A pergunta que nos interessará é a seguinte: a carga em cada linha é a mesma para células diferentes ao formar uma lista de todas as soluções completas? Obviamente, quanto maior o valor da frequência, maior a atividade dessa célula na formação de uma lista de soluções completas. Para estabelecer isso, determinamos para cada linha, com base em uma lista de todas as soluções completas, a frequência relativa dos vários índices. Primeiro, analisamos uma matriz de solução de tamanho n = 8. Vamos examinar cada linha da matriz de soluções completas sequencialmente e determinar a frequência de vários valores de índice. A Tabela 2 mostra os valores correspondentes das frequências absolutas de atividade de diferentes células em cada uma das oito linhas e na Fig. 8
Tabela 2. Frequência absoluta de atividade celular em cada uma das oito linhas da matriz de decisão 8x8, com base em uma análise da lista de todas as soluções completas
| linha \ col | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 | 4 | 8 | 16 | 18 | 18 | 16 | 8 | 4 |
| 2 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 3 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 4 | 18 | 8 | 12 | 8 | 8 | 12 | 8 | 18 |
| 5 | 18 | 8 | 12 | 8 | 8 | 12 | 8 | 18 |
| 6 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 7 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 8 | 4 | 8 | 16 | 18 | 18 | 16 | 8 | 4 |
é apresentado um grupo de 4 gráficos, em que cada gráfico caracteriza a mudança nas frequências relativas em uma linha. Uma das conclusões fundamentalmente importantes que podem ser extraídas da análise de todos os dados obtidos é a seguinte:
- para uma matriz de decisão de tamanho arbitrário n , a atividade das células da i- ésima linha coincide com a atividade da célula n-i + 1 , isto é, a atividade das células da primeira linha sempre coincide com a atividade das células da última linha, respectivamente, a atividade das células da segunda linha coincide com a atividade das células da penúltima linha, etc.
Se n for ímpar, apenas a linha mediana da matriz da solução não possui um par simétrico; para todas as outras células, a regra acima é válida - Chamamos isso de “propriedade da simetria horizontal da atividade das células de diferentes linhas da matriz da solução” . Por esse motivo, apresentamos apenas 4 gráficos para a matriz de decisão de tamanho n = 8, uma vez que os gráficos correspondentes da atividade celular das linhas (1, 8), (2,7), (3,6) e (4,5) são completamente idênticos.
Deve-se notar também que os valores de frequência são simétricos em relação ao eixo vertical, dividindo a matriz em duas partes iguais (no caso de um valor par de n) ou passando pela coluna mediana (no caso de um valor ímpar de n). Chamamos isso de “propriedade de simetria vertical da atividade das células de diferentes linhas da matriz da solução” .
Além disso, como segue a análise da Tabela 2, as frequências na matriz da solução são simétricas em relação às diagonais principais esquerda e direita.
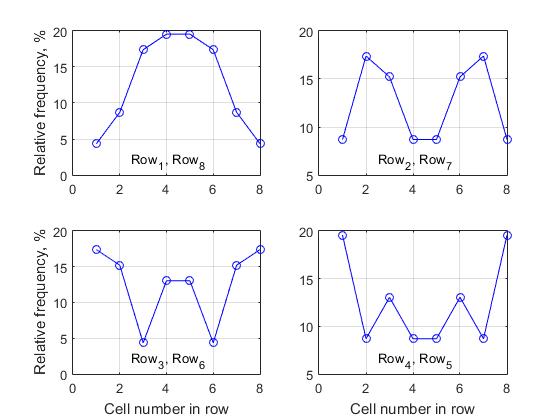
Fig. 8 Atividade celular das linhas correspondentes ao formar a lista de soluções completas, n = 8
Penso que a presença de regras restritivas na declaração do problema e a propriedade relacionada do não determinismo "formam" um tipo de relacionamento harmonioso entre nós em diferentes linhas. Os ramos da pesquisa que se encaixam nessas regras - levam à formação de uma solução completa. Os demais ramos da pesquisa, em algum momento, violam essas regras e, como resultado, "concluem sua jornada" na forma de decisões breves. Deve-se notar aqui que as células da matriz de decisão têm apenas um relacionamento local dentro do grupo de influência da projeção; não há regras prescritas para ações coordenadas entre elas. A atividade coletiva das células é apenas uma consequência do resultado da influência de regras restritivas. Portanto, permanece uma questão bastante interessante: como regras restritivas, como fatores não determinísticos, afetam as células da matriz de decisão, o que leva à formação de uma matriz de atividade celular “harmoniosa” - simétrica em relação aos eixos horizontais e verticais e também à esquerda e diagonais principais direitas. Essa é uma propriedade característica apenas desse problema ou também vale para outros problemas não determinísticos?
9. A partir de qual número de linha o algoritmo de rastreamento Forward - Back tracking é ativado?
Se seguirmos a operação do algoritmo de seleção de linha sequencial na matriz de decisão para a localização da rainha, podemos ver que a partir de uma determinada linha, que chamaremos de "StopRow", o processo de avançar é "travado". No ramo de pesquisa, esta é a primeira linha em que há problemas com a disponibilidade de aplicativos gratuitos.

Fig. 9-1 Dependência da proporção do índice StopRow en no tamanho da matriz de decisão (parte 1)
posição para a localização da rainha. É a partir dessa linha que o algoritmo Back tracking é ativado para limpar os rastreamentos das ações executadas anteriormente e retornar. Essa é a linha na qual a primeira solução curta aparece.
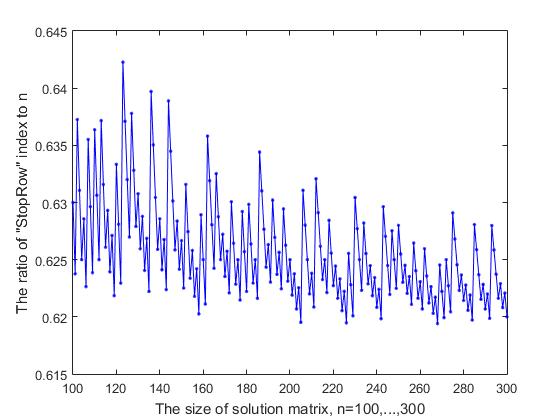
Fig. 9-2 Dependência da razão do índice StopRow em relação ao tamanho da matriz de decisão (parte 2)
O índice da linha “StopRow”, com o qual as dificuldades começam a avançar, depende do tamanho n da matriz de decisão. Se considerarmos a razão desse índice, que indicamos por StopInd, para o tamanho da matriz da solução n, como pode ser visto na Figura 9-1, onde são apresentados os resultados dos cálculos para os valores iniciais n = (7, ..., 99), essa proporção varia em maior ou menor grau. lado e tende a diminuir. Com um aumento em n = (100, ..., 300), essa relação varia entre 0,619 - 0,642 (Fig. 9-2) e, com um aumento adicional em n, obtemos os seguintes resultados (os valores de n são dados em sequência e o valor entre parênteses é Razão StopInd e StopInd / n: 1000 (619, 0,6190), 2000 (1239, 0,6195), 3000 (1856, 0,6187), 4000 (2473, 0,6182), 5000 (3091, 0,6182) Surpreendentemente, pode-se argumentar que parar -line divide a matriz de decisão de acordo com a regra da proporção áurea : a proporção StopInd / n difere de (n-StopInd) / StopInd por uma pequena quantidade que tende a zero com o aumento de n. Por exemplo, para n = 5000, a diferença entre as relações 3091/5000 e 1909/3091 é 0,006, que é menor que 0,1% da média dessas duas relações.
O gráfico mostrado nas duas figuras 9- (1,2) tem uma forma não aleatória de variabilidade, que se assemelha a uma gravação em uma "pauta musical". Saltos repetidos para cima e para baixo gradualmente são visíveis com alguma periodicidade irregular. Obviamente, há alguma razão para esse tipo de comportamento em curva, e talvez isso seja de interesse para a pesquisa. Por esse motivo, para fins de visualização mais detalhada, o gráfico foi apresentado em duas figuras.
Eu considerei apenas uma parte das perguntas que podem ser formuladas com base nos resultados da solução do problema "na distribuição de n rainhas". Espero que os resultados obtidos tornem os mecanismos de formação de processos não determinísticos e mudanças no espaço de estados mais transparentes para a compreensão. Talvez isso sirva de incentivo para a formulação de novas tarefas e para o futuro.
Conclusão
- Se, olhando a publicação, chegamos a uma conclusão, então naturalmente surgirá a pergunta: "o que significa a Solução de Problemas de Um Bilhão de Rainhas no título do artigo?" Ao preparar a publicação para Habr, pensei que uma pessoa que tivesse, por exemplo, uma mina onde são extraídos diamantes, deveria dar pelo menos um diamante para seus amigos e parentes, caso contrário, seria injusto. Portanto, eu gostaria de apresentar um presente a todos os membros da comunidade habr: participantes, organizadores, visitantes. Como o nome indica, esta é a solução para o problema de distribuir um bilhão de rainhas em um tabuleiro de xadrez de bilhões de bilhões de dólares.
É claro que este não é um diamante facetado, mas para os verdadeiros conhecedores da arte intelectual, pode ser mais valioso do que "algum tipo de diamante lá". Além disso, os diamantes são muito diferentes em todo o mundo, e essa solução está apenas em uma cópia até agora. E nosso Deus Byte (*) vê que estou fazendo isso sinceramente.
A solução resultante é uma matriz unidimensional de um bilhão de números, apresentada no formato MatLab .mat e disponível em: One Billion Queens Problem Solution no Google Drive
-O primeiro elemento desta matriz caracteriza a posição da rainha na primeira linha, o segundo elemento - a posição na segunda linha, etc. Esta é apenas uma solução dentre as nBilhões de soluções possíveis. E o valor de nBilhões é um número tão grande que pode ser considerado um parente próximo do infinito.
- Parece-me que esta solução pode ser atribuída à categoria de valores intelectuais virtuais. Podemos dizer que "isso é algo em que há algo". Eles realmente não podem ser "tocados", de modo que são percebidos na consciência apenas no nível das sensações. Ali, de fato, há uma ordem surpreendente e harmonia explícita e implícita. Este é um presente puramente simbólico (literal e figurativamente), dirigido a todos os membros da comunidade. Eu penso: " Você não é como todo mundo ".
(Espero que alguém "leve o presente para casa". O arquivo é grande o suficiente - 3,7 Gb. São dados limpos e verificados. O Google Drive exibirá avisos - trate-o com compreensão)
- Antes de tomar essa decisão, pensei na natureza coletiva individual de um presente. É possível que um seja apresentado com o original e o restante com cópias? Mas a solução foi simples. Os conceitos "cotidianos" usuais de "original" e "cópia", nesse caso, perdem o significado. Não copiamos, mas criamos outro original. E os "originais" são iguais para todos e igualmente equivalentes.
- Eu acho que na companhia de parentes, você provavelmente será o único que recebeu um "produto intelectual" como presente. Será divertido se você contar à sua sogra sobre esse presente: “Imagine o tabuleiro de xadrez de uma mãe medindo 50.000 km por 50.000 km, no qual 1 bilhão de rainhas são distribuídas de tal maneira que uma não se vê de perto ...”. Quem sabe, talvez depois disso, o genro seja mais apreciado, pois ele recebe um presente tão estranho.
Desejo a todos os membros da comunidade habr saúde, sucesso e bem-estar. Que o ano novo traga boa sorte a todos nós.
(*) - Como se refere ao nome do objeto, sua descrição também deve ser fornecida.
Byte Deus significa uma entidade multidimensional, composta por zeros e uns, razoável em todos os sentidos e infinita em todas as direções. Qualquer sequência de zeros e uns neste espaço representa certo conhecimento.
Referências
[4] Max Bezzel, Proposta do problema das 8 rainhas ", Berliner Schachzeitung, Volume
3 (1848), página 363. (Enviado sob o nome do autor \ Schachfreund ".)
[5] Franz Nauck, Briefwechseln mit allen fur all ", Ilustração ilustrada, Volume.
377 Número 15 (1850), página 182.
[6] Bell Jordan; Stevens Brett (2009). "Uma pesquisa de resultados conhecidos e áreas de pesquisa para n-rainhas". Matemática Discreta. 309 (1): 1–31
[7] Gent, Ian P.; Jefferson, Christopher; Nightingale, Peter (agosto de 2017). "Complexidade da conclusão n-Queens". Journal of Artificial Intelligence Research. AAAI Pressione. 59: 815-848
[8] W. Kosters e todos, n-Queens - 342 referências (20 de novembro de 2018)
[9] NJA Sloane, a enciclopédia on-line de seqüências inteiras, publicada eletronicamente. 2016