Modelos Matemáticos do Caos

1. Introdução

Habr já discutiu a teoria do caos em artigos [1,2,3]. Os seguintes aspectos da teoria do caos são considerados nesses artigos: diagrama generalizado do gerador Chua; modelar a dinâmica do sistema Lorentz; atratores programados pelos circuitos lógicos Lorentz, Ressler, Rikitake e Nose-Hoover.

No entanto, técnicas da teoria do caos também são usadas para modelar sistemas biológicos, que, sem dúvida, são um dos sistemas mais caóticos de tudo o que se pode imaginar. Sistemas dinâmicos de equalização foram usados ​​para modelar tudo, desde crescimento populacional e epidêmico até batimentos cardíacos arrítmicos [4].

De fato, quase todo sistema caótico pode ser modelado - o mercado de valores mobiliários gera curvas que podem ser facilmente analisadas usando atratores estranhos, o processo de soltar quedas de uma torneira vazando é aleatório quando analisado com a orelha nua, mas se retratado como um atrator estranho, ele abre uma ordem sobrenatural que não se poderia esperar dos meios tradicionais.

O objetivo deste artigo é considerar a teoria do caos usando o exemplo de aumentar o número de populações biológicas e dobrar o ciclo em sistemas mecânicos com visualização gráfica de modelos matemáticos com base em programas simples e intuitivos escritos em Python.

O artigo foi escrito com o objetivo de ensinar, mas permitirá que mesmo um leitor sem experiência em programação use os programas acima para resolver independentemente a maioria dos novos problemas educacionais sobre o tópico modelagem de fenômenos do caos.

Dobrar o período de ciclos e caos no exemplo do crescimento do número de populações biológicas

Vamos começar examinando a equação diferencial logística que modela um aumento limitado e não exponencial no número de populações biológicas:

$$$\ frac {dN} {dt} = aN-bN ^ {2}, (a, b> 0). (1)$

É essa equação que pode prever padrões de comportamento exóticos e inesperados de algumas populações. De fato, de acordo com (1), para $$$t \ rightarrow + \ infty$ o tamanho da população se aproxima do limite igual a / b .

Para a solução numérica da solução diferencial logística, você pode usar o algoritmo mais simples, com o valor numérico da etapa do tempo, considerando $$$t_ {n + 1} = t_ {n} + h$ , a solução (1) pode ser obtida aplicando repetidamente a seguinte relação:

$$$N_ {n + 1} = N_ {n} + (aN_n-bN {_ {n}} ^ {2}) h.$ 2)

Representamos a equação (2) na forma de uma equação logística em diferenças finitas:

$$$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$ . (3)

onde: r = 1 + ah es = bh .
Substituição em (3) $$$N_ {n} = \ frac {r} {s} x_ {n}$ obtemos a fórmula iterativa:

$$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ (4)

Calculando os valores dados pela relação (3), podemos gerar uma sequência $$$x_ {1}, x_ {2}, x_ {3}, .....$
os valores máximos do número de populações que o ambiente suportará em determinados momentos $$$t_ {1}, t_ {2}, t_ {3}.$ .

Assumimos que existe um valor limitador de frações que expressa uma parte do tamanho da população:

$$$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$ (5)

Vamos investigar como isso depende $$$x _ {\ infty}$ do parâmetro de crescimento r na equação (4). Para fazer isso, em Python, escrevemos um programa que, começando com $$$x_ {1} = $ 0,$ calcula os resultados em várias centenas de iterações ( n = 200 ) para r = 1,5; 2,0; 2,5 :


O resultado do programa (para reduzir a saída dos resultados, são fornecidos os três primeiros e os quatro últimos valores):

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000 

Uma análise do modelo discreto mostra que para r = 1,5; 2,0; 2,5 com número crescente de iterações, o valor $$$x_ {n}$ estabiliza e se torna quase igual ao limite $$$x _ {\ infty}$ , que é determinado pela relação (5). Além disso, para os valores dados de r, a quantidade $$$x _ {\ infty}$ correspondentemente igual $$$x _ {\ infty} = 0,3333; 0,5000; $ 0,600$ .
Aumentamos r = 3,1; 3,25; 3,5 e o número de iterações n = 1008; para isso, fazemos as seguintes alterações no programa:


O resultado do programa (para reduzir a saída dos resultados, são fornecidos os quatro primeiros e os últimos oito valores):

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269 

Como se segue a partir dos dados acima, em vez de estabilizar perto de uma única população limitante, a parte fracionária da população flutua entre duas frações à medida que o tempo muda. Comparado com r = 3,1 , o período do ciclo para r = 3,25 duplica e para r = 3,5 quatro vezes.


O resultado do programa:



Devido à duplicação do período de iteração, $$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ tornou-se amplamente conhecido. Quando o valor da taxa de crescimento excede r = 3,56 , a duplicação do período acelera e o caos extremo já surge no ponto r = 3,57 . Para exibir o início do caos, usamos o seguinte programa:


O resultado do programa:

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397 

Escreveremos um programa para visualizar a dependência do comportamento da iteração no parâmetro de crescimento r . Para cada valor de r no intervalo $$$a \ leqslant r \ leqslant b$ 1000 iterações são executadas para obter estabilidade. Em seguida, todos os 250 valores obtidos como resultado de iterações são plotados ao longo do eixo vertical, formando pontos ( r, x ):


O resultado na forma de um diagrama:



O gráfico resultante é chamado de "diagrama de ramificação" , que permite determinar se um determinado valor de r corresponde a um ciclo ou caos. O único valor do tamanho da população é determinado pelo valor $$$r \ aproximadamente 3$ depois um ciclo com um período de 2 a $$$r \ aproximadamente 3,4$ , depois um ciclo com um período de 4, depois um ciclo com um período de 8 em diante, com uma abordagem rápida ao caos.

Deve-se notar que as áreas verticais do espaço não preenchido no gráfico são as regiões r = 3,6 er = 3,7 , entre r = 3,7 er = 3,8 , entre r = 3,8 er = 3,9 onde a ordem cíclica retorna do caos anterior.
Considerar a aparência de um ciclo com um período múltiplo de 3 na região $$$3,8 \ leqslant r \ leqslant $ 3,$ faça alterações no programa anterior:


O resultado do programa:



O ciclo do período 3 aparece nas proximidades do ponto r = 3,83 e, em seguida, é dividido seqüencialmente em ciclos 6,12,24. A existência de um ciclo com o período 3 implica a presença de ciclos de qualquer outro período finito, bem como ciclos caóticos sem nenhum período.

O diagrama de ramificação permite acompanhar o desenvolvimento do sistema com uma mudança suave no parâmetro. Com um valor fixo do parâmetro, o diagrama de aranha (diagrama de Lamera) permite rastrear as órbitas dos pontos.

A construção de um diagrama de aranha permite identificar vários efeitos que são invisíveis no diagrama de ramificação. Vamos escrever um programa:


Diagrama Lamera:

Período duplicado em sistemas mecânicos

Considere uma equação diferencial que modela as vibrações amortecidas livres de um ponto material de uma determinada massa em uma mola não linear, na qual o amortecimento é determinado pela velocidade.

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$ (6)

Na equação (6), o termo kx representa a força de uma mola linear aplicada a um ponto material de uma dada massa e o termo $$$\ beta x ^ {3}$ representa a não linearidade real da primavera.

Se uma força atua no sistema de oscilações livres (6), o deslocamento do ponto do material da massa à qual essa força é aplicada é descrito pela equação diferencial de Duffing para oscilações forçadas:

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$ (7)

A equação (7) para a maioria dos parâmetros incluídos é resolvida numericamente. O sistema mecânico para o modelo matemático de acordo com a equação (7) é mostrado na figura:



Uma característica do sistema fornecido é que, em vez de uma mola, é usada uma rosca de metal flexível, que oscila em um plano vertical, para o qual a constante de gancho k é negativa. Nesse esquema, os pontos de equilíbrio estável (a) e (c) e o ponto de equilíbrio instável (b).

Quando um ponto material é deslocado da posição (b), a força que atua sobre ele é repulsiva. Se a força periódica, por exemplo, criada pelo campo magnético oscilante for parcialmente amortecida pela resistência do ar. Então, a equação (7) é um modelo matemático aceitável para o deslocamento horizontal x (t) de um ponto de material com os seguintes intervalos de parâmetros $$$k <0, c> 0, \ beta> 0$ .

Para estudar o comportamento de um sistema não-linear, tomamos $$$k = -1, m = c = \ beta = \ ômega = 1$ então a equação diferencial (7) assume a forma:

$$$x ^ {''} + x ^ {'} - x + x ^ {3} = F_ {0} cos (t)$ (8)

Escrevemos um programa para a integração numérica da equação (8) nas condições iniciais $$$x (0) = 1, x ^ {'} (0) = 0$ no campo $$$100 \ leqslant t \ leqslant 200$ e para cada um dos seguintes valores de amplitude $$$F_ {0} = 0,6; 0,7; 0,75; 0,8$ e, em cada caso, plote as soluções para os planos $$$x (t), x ^ {'} (t)$ e $$$t, x (t)$ :


Gráficos como resultado do programa





Essa transição do período de duplicação para o caos mostra o comportamento geral de um sistema mecânico não linear em resposta a uma alteração no parâmetro físico correspondente, por exemplo: $$$k, m, c, \ beta, \ ômega, F_ {0}$ . Tais fenômenos não ocorrem em sistemas mecânicos lineares.

Atrator Lorenz

A substituição na equação de Duffing por oscilações forçadas (7) leva a um sistema bidimensional não linear de equações diferenciais, que foi mostrado na listagem anterior. Um sistema tridimensional não linear de equações diferenciais aplicado a problemas meteorológicos foi considerado por E.N. Lorenz:

$$$\ frac {dx} {dt} = - sx + sy,$
$$$\ frac {dy} {dt} = - xz + rx-y,$ (9)
$$$\ frac {dz} {dt} = xy-dz$

A solução do sistema (9) é melhor visualizada na projeção em um dos três planos. Escrevemos um programa de integração numérica para os valores dos parâmetros b = \ frac {8} {3}, s = 10, r = 28 e as condições iniciais x (0) = - 8, y (0) = 8, z (0) = 27 :


O resultado do programa:



Considerando a imagem no gráfico ao longo do tempo, pode-se supor que o ponto P (x (t), y (t), z (t)) faça um número aleatório de oscilações, direita ou esquerda. Para uma aplicação meteorológica do sistema Lorenz, após um número aleatório de dias claros, segue-se um número aleatório de dias chuvosos.

Considere um programa para mapear o atrator Lorentz no plano xyz para condições iniciais ligeiramente diferentes:


Os resultados do programa são mostrados nos seguintes gráficos:





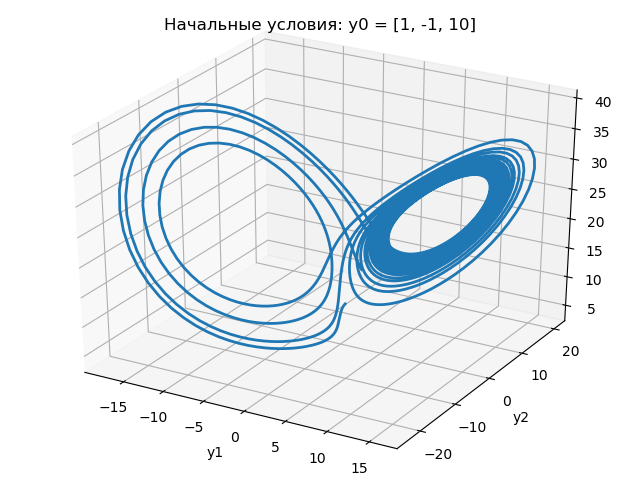
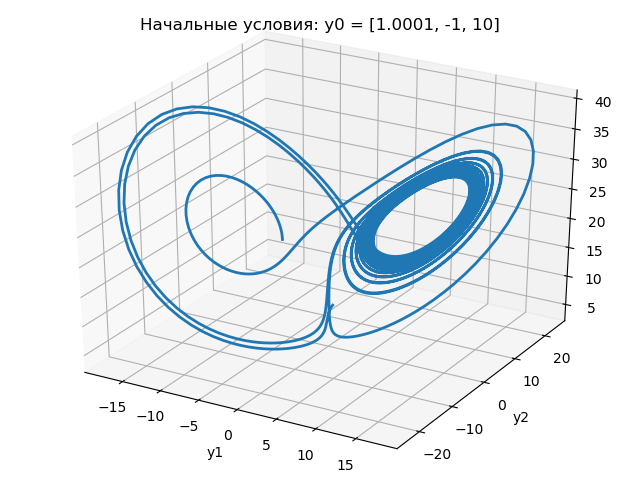
A partir dos gráficos acima, conclui-se que uma mudança na condição inicial de 1,0 para 1.0001 altera drasticamente a natureza da mudança no atrator de Lorentz.

Sistema Rossler

Este é um sistema tridimensional não linear muito estudado:
$$$\ frac {dx} {dt} = - y-z,$
$$$\ frac {dy} {dt} = x- \ alpha y,$ (10)
$$$\ frac {dz} {dt} = b + x (x-c).$

Escreveremos um programa para a integração numérica do sistema (10) para os seguintes parâmetros a = 0,39, b = 2, c = 4 nas condições iniciais x (0) = 0, y (0) = 0, z (0) = 0 :


O resultado do programa:



No avião, a fita de Rossler parece um laço, mas no espaço acaba sendo torcida como uma fita de Moebius.

Conclusões

Para demonstrar o fenômeno do caos, são apresentados programas simples e intuitivos em uma linguagem de programação Python de alto nível, fáceis de atualizar para novos projetos sobre esse tópico. O artigo tem foco educacional e metodológico e pode ser usado no processo de aprendizagem.

Referências

1. Um pouco sobre o caos e como criá-lo
2. Um olhar crítico sobre o atrator Lorenz
3. Geradores de caos FPGA
4. Equações diferenciais e problemas de valor-limite: modelagem e cálculo usando o Mathematica, Maple e MATLAB. 3ª edição.: Per. do inglês - M .: LLC “I.D. Williams, 2008. - 1104 p .: III. Paral. tit. Inglês