Em um ponto, durante o desenvolvimento do jogo, eu me deparei com a questão do desempenho em PCs modernos. Nosso modelador possui um computador de montagem vermelho moderno bastante poderoso. Mas ele teve nosso projeto terrivelmente lento, carregando um núcleo de processador.
O motivo é simples - os novos processadores possuem muitos núcleos, mas na verdade são menos eficientes em aplicativos de thread único. Naquela época, eu tinha uma renderização em um fluxo. Mas, de fato, as razões não estavam muito nisto. E, no processo de encontrar o problema, decidi calcular quantos polígonos estão presentes na cena:
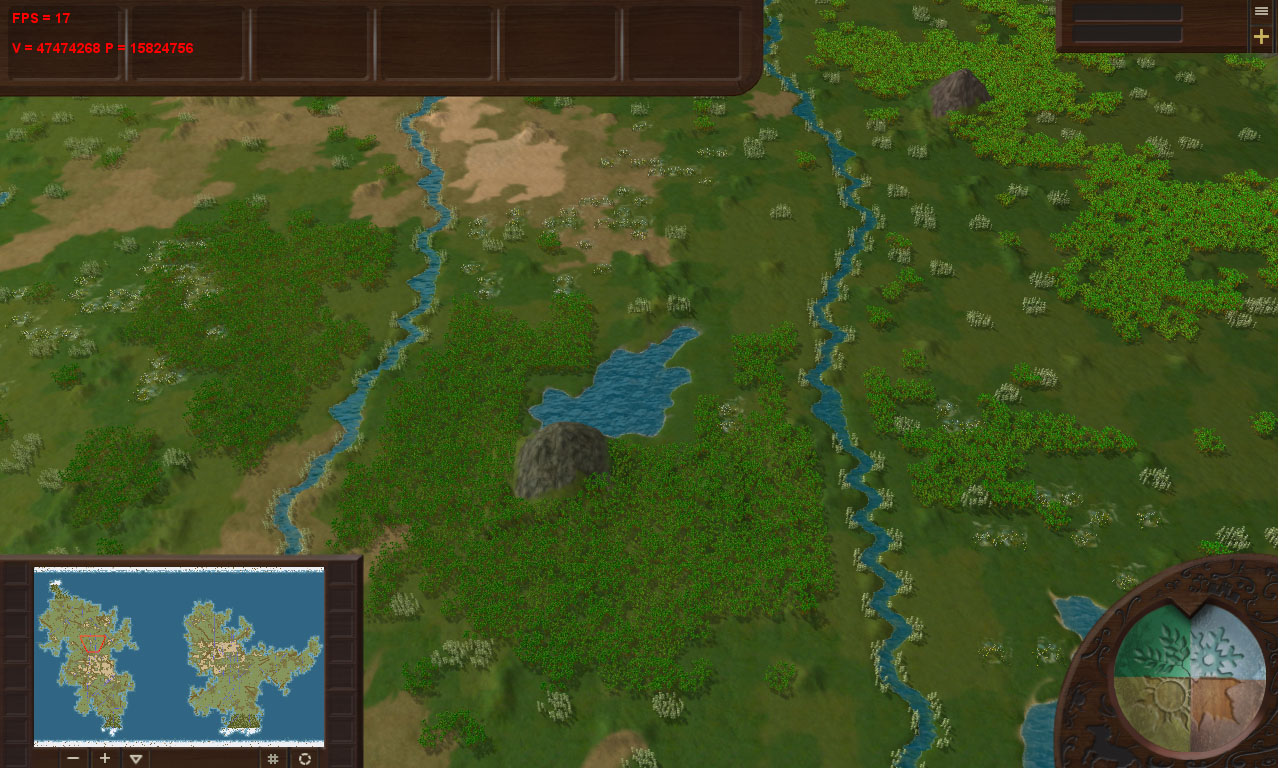
No mapa médio do jogo, com a distância máxima e com um grande conjunto de palmeiras -
15 824 756 triângulos! Quase 16 milhões! Um número enorme.
Tendo brincado um pouco com o gerador de mapas, consegui encontrar um lugar com 16,75 milhões:
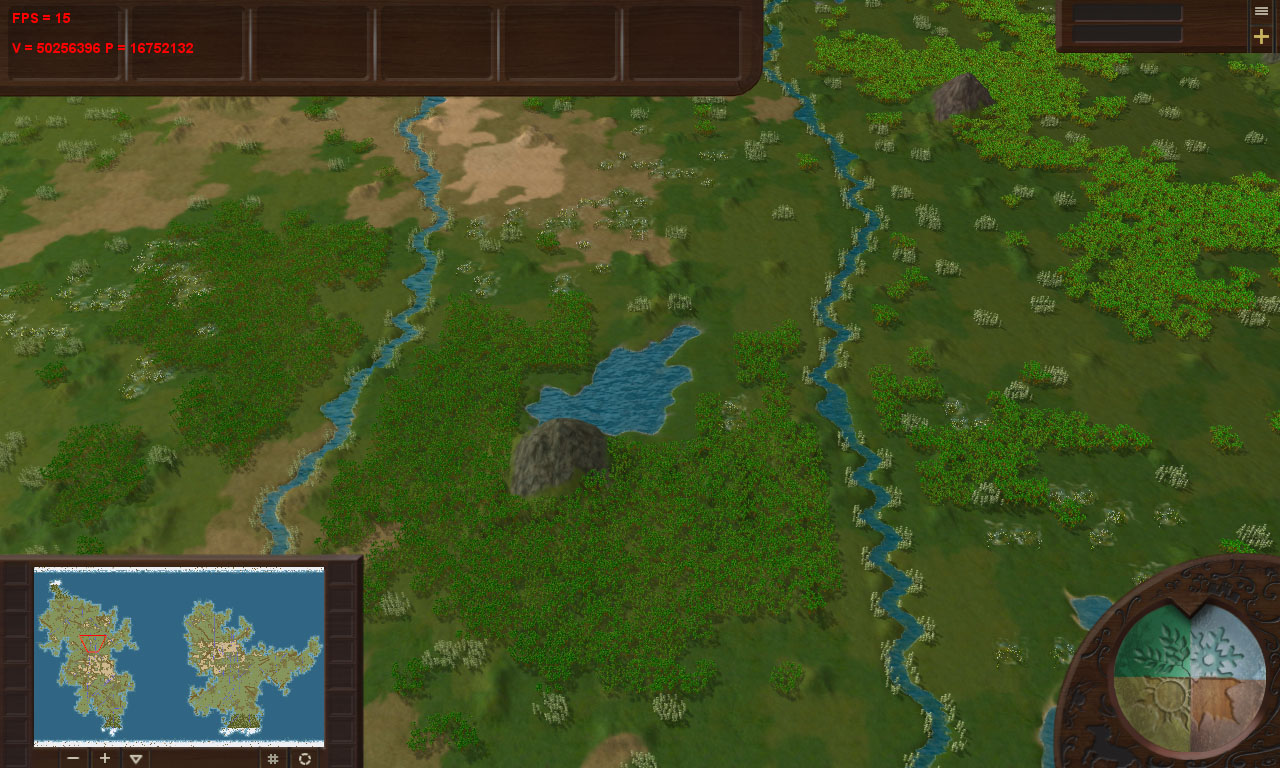
Embora, aqui, um lugar semelhante com árvores de Natal tenha dado apenas 8,5 milhões de triângulos:
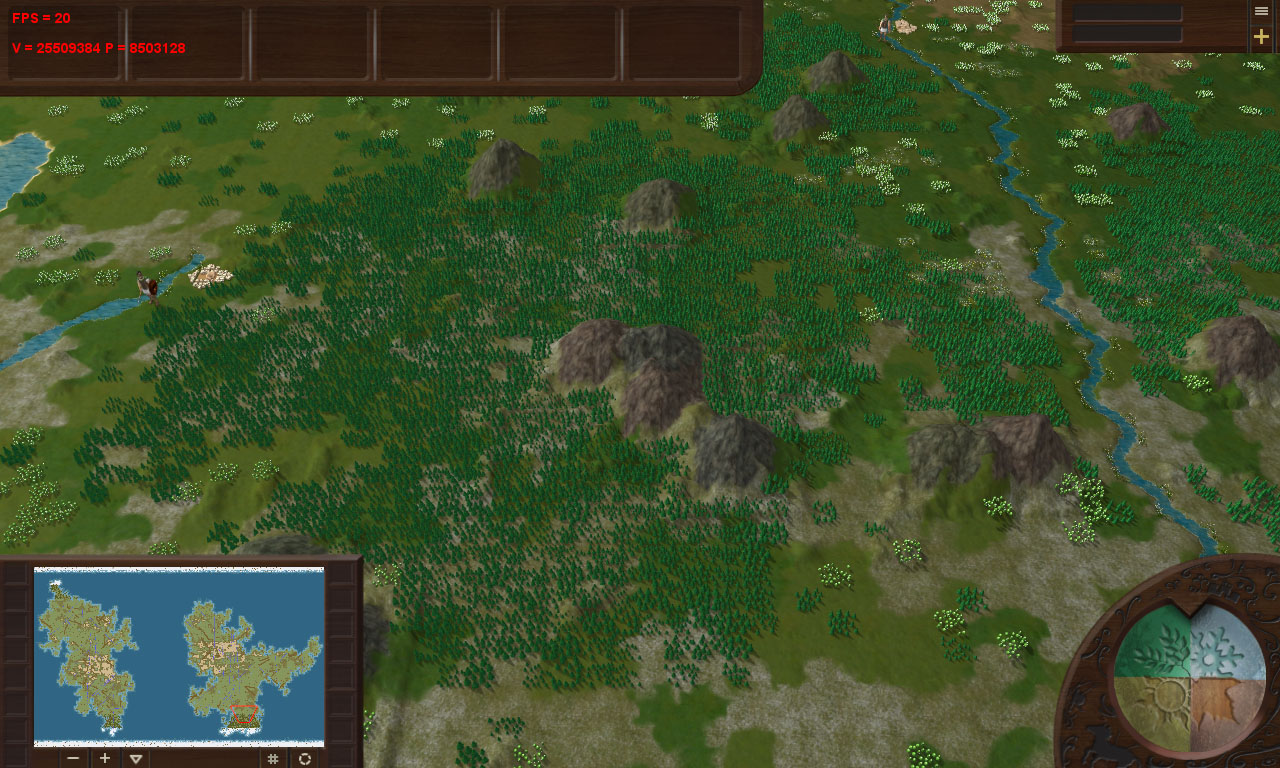
A cena média consistia em ~ 4 milhões:
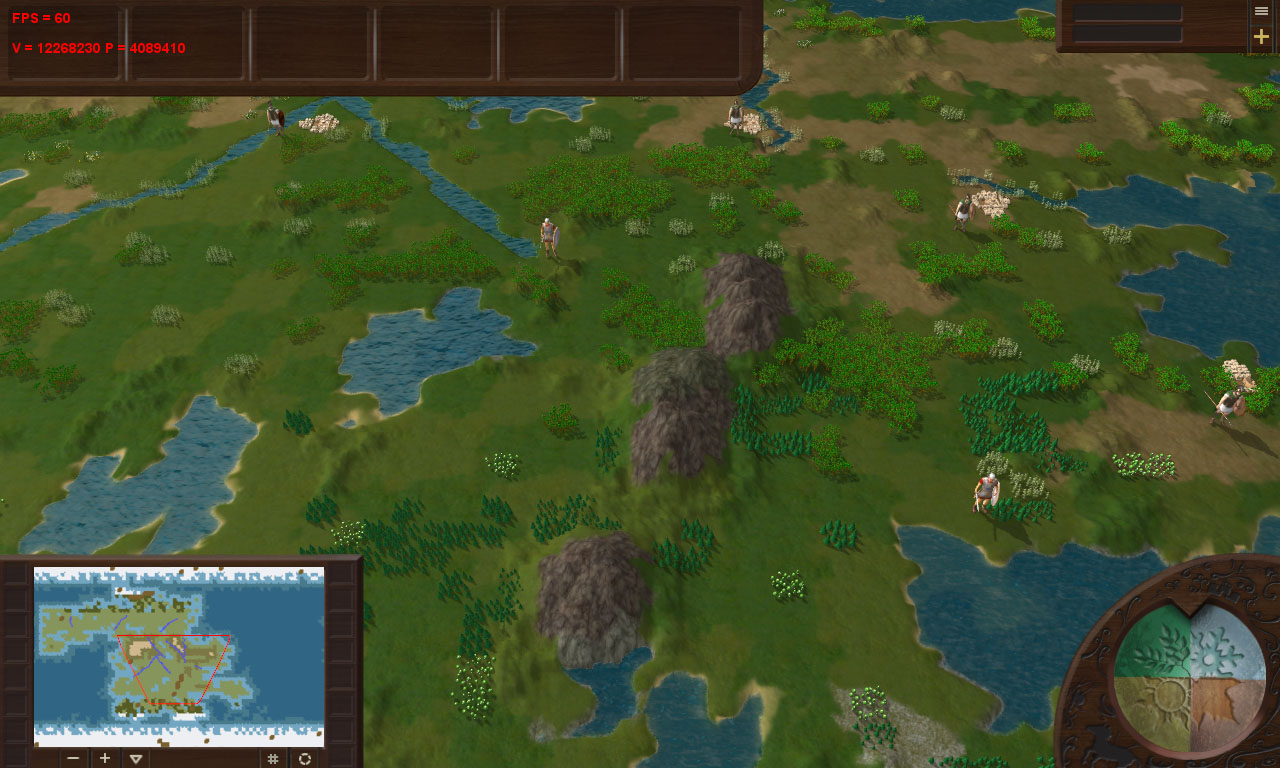
Em geral, fiquei feliz que minha renderização estivesse lidando com um número tão grande de triângulos, mas o número deles era excessivo. A solução estava na superfície:
- Otimize o número de polígonos nos modelos.
- Otimize a malha poligonal da paisagem.
- A implementação da renderização multithread.
Para aqueles que podem não estar interessados no primeiro parágrafo do nosso programa de otimização, por exemplo, especialistas inexperientes, recomendo ir com segurança para a segunda parte.
1. Otimização do número de polígonos nos modelos
Em nosso motor, a vegetação é desenhada em "pacotes", toda a paisagem é dividida em ladrilhos e sub-ladrilhos, o pacote mínimo é um sub-ladrilho.

Um pacote é uma malha, pois reduzir o número de malhas reduz significativamente o número de chamadas de CPU-> GPU.

Inicialmente, nossas árvores consistiam em cones truncados, movendo-se para cones completos, conseguimos remover alguns triângulos extras:

A cereja no bolo foi a decisão de remover os troncos das árvores, porque com o ângulo da câmera eles simplesmente não eram visíveis.
Como resultado, conseguimos reduzir em 40% o número de polígonos, em um pacote de árvores de Natal. As diferenças são quase invisíveis:

Com as palmeiras, era mais difícil, mas pacotes de 5000 - 6000 polígonos precisavam ser consertados. Como alcançar a massa e a densidade da selva? A alta densidade da selva foi alcançada devido ao grande número de palmeiras:

Decidimos simplificar as palmas das mãos e introduzir uma segunda camada de vegetação, o que nos permitiu manter a densidade visível e alcançar os 600 - 700 polígonos desejados por pacote.

Reduzir o número de polígonos em 10 vezes é um excelente resultado.

2. Otimização do cenário de malha poligonal
Inicialmente, a grade da paisagem era:

A captura de tela mostra seções simples da paisagem, são telhas de prados, planícies, embora outras superfícies lisas. Decidi remover pequenas irregularidades na paisagem. Assim, ele aumentou a área dos mesmos ladrilhos de altura. Não verificando astuciosamente todos os vértices dos ladrilhos e sub-ladrilhos quanto à igualdade na altura, consegui alcançar este resultado:
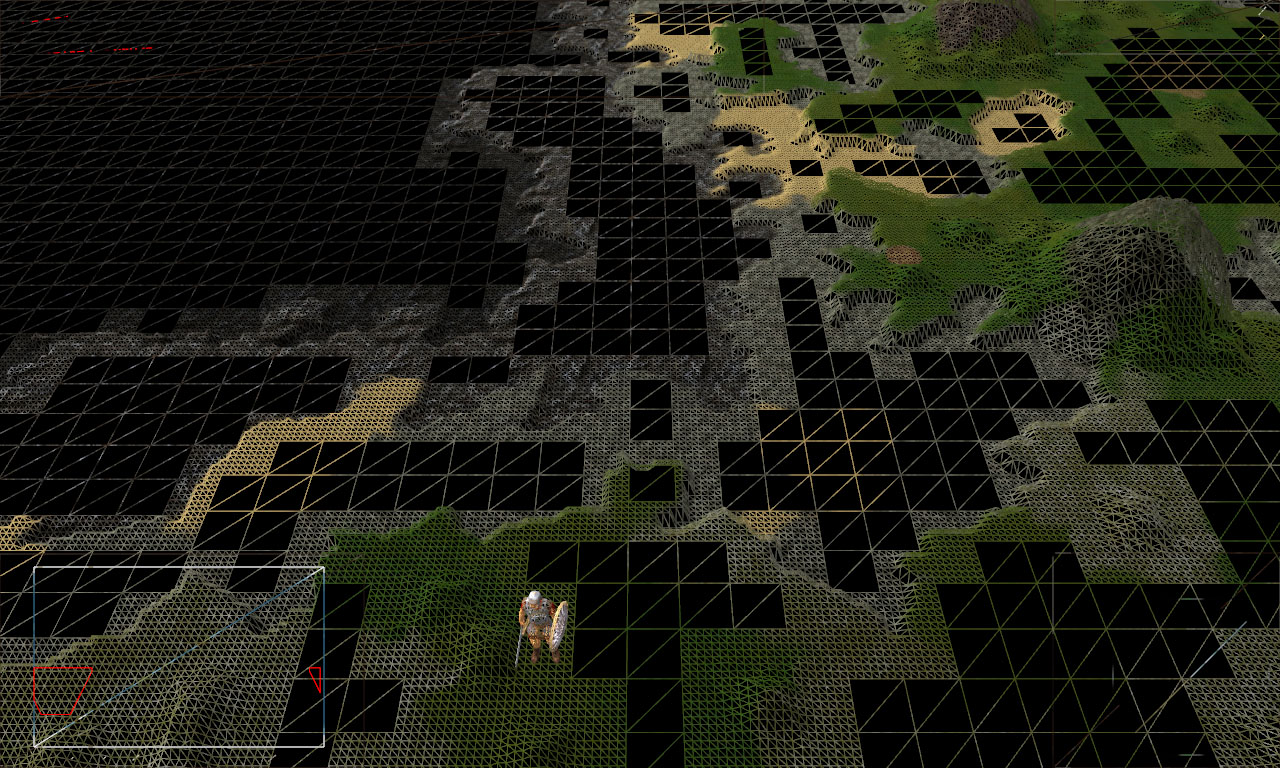
Ainda havia lugares planos que poderiam ser otimizados, e comecei a construir polígonos a partir desses triângulos que tinham a mesma altura. Um ladrilho foi retirado e todos os seus triângulos foram classificados em uma matriz de triângulos de altura desigual e uma lista de matrizes consistindo em altura igual e triângulos adjacentes.

No exemplo dado, descobriu-se: 1 matriz de triângulos que não podem ser alterados, uma vez que tinham todas as alturas diferentes (triângulos vermelhos) e uma lista composta por duas matrizes de triângulos com a mesma altura (as matrizes são preenchidas com cores).
Agora, a tarefa era encontrar, a partir da matriz de triângulos, seu contorno côncavo-côncavo (casco côncavo), e muitos triângulos poderiam ter orifícios. Anteriormente, encontrei o Convex Hull em meu trabalho, não havia problemas com eles, eu já usava o algoritmo Graham. Mas houve problemas com a construção do casco côncavo ... Foi bastante difícil encontrar informações sobre esse tópico na Internet. Eu tive que escrever uma implementação de algoritmos do zero. Não mentirei se disser que li cerca de dez dissertações diferentes sobre esse assunto. Mas todos os algoritmos propostos deram um resultado aproximado com algum erro. Depois de uma semana de tormento e dor, tive a ideia do meu algoritmo.
Tentei construir um contorno a partir do conjunto de vértices dos triângulos, ou seja, Traduzi a matriz de triângulos em uma matriz de vértices e já construí uma concha sobre eles. Mas, para minha tarefa, isso não foi necessário. De acordo com minhas conclusões, construir uma concha diretamente a partir de triângulos era mais fácil e a precisão do casco côncavo era de 100%.
Inicialmente, eu queria colocar uma colcha de retalhos do código fonte do algoritmo aqui, mas parece mais fácil descrevê-lo em poucas palavras: base é a regra: se o vértice de um triângulo for incluído em quatro ou menos triângulos, uma das arestas que formam o vértice fica na borda. Em seguida, é formada uma lista dessas arestas, levando em consideração a remoção de arestas idênticas. Encontramos a aresta com o menor X e Y e a partir dela iniciamos a passagem / classificação das arestas com a adição de vértices exclusivos à lista. Esta lista será a concha de muitos triângulos. A única coisa na final é remover pontos colineares da lista.
Como resultado disso, eu pude construir o Casco Côncavo de quase qualquer complexidade. Esse algoritmo não se encaixava em um conjunto de furos, mas eu resolvi isso simplesmente dividindo esse conjunto em duas metades em um buraco. Então peguei o circuito e o triangulei:
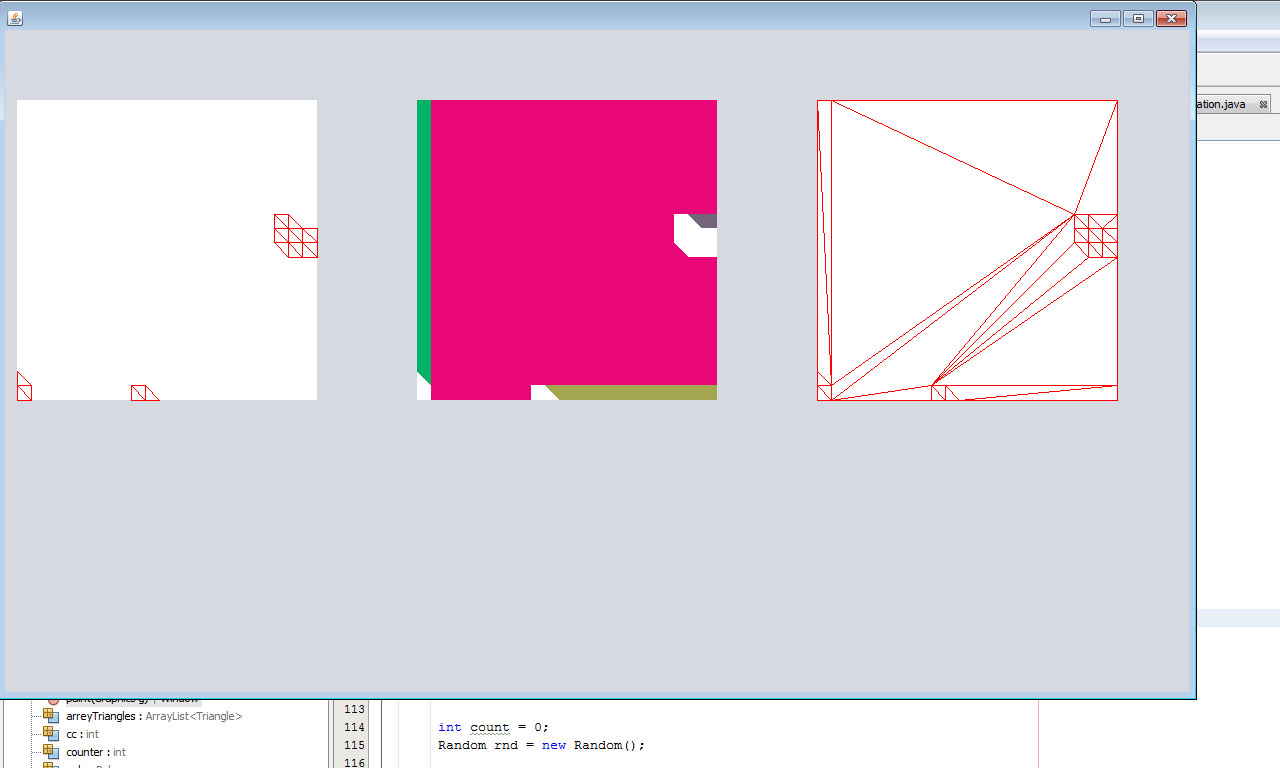
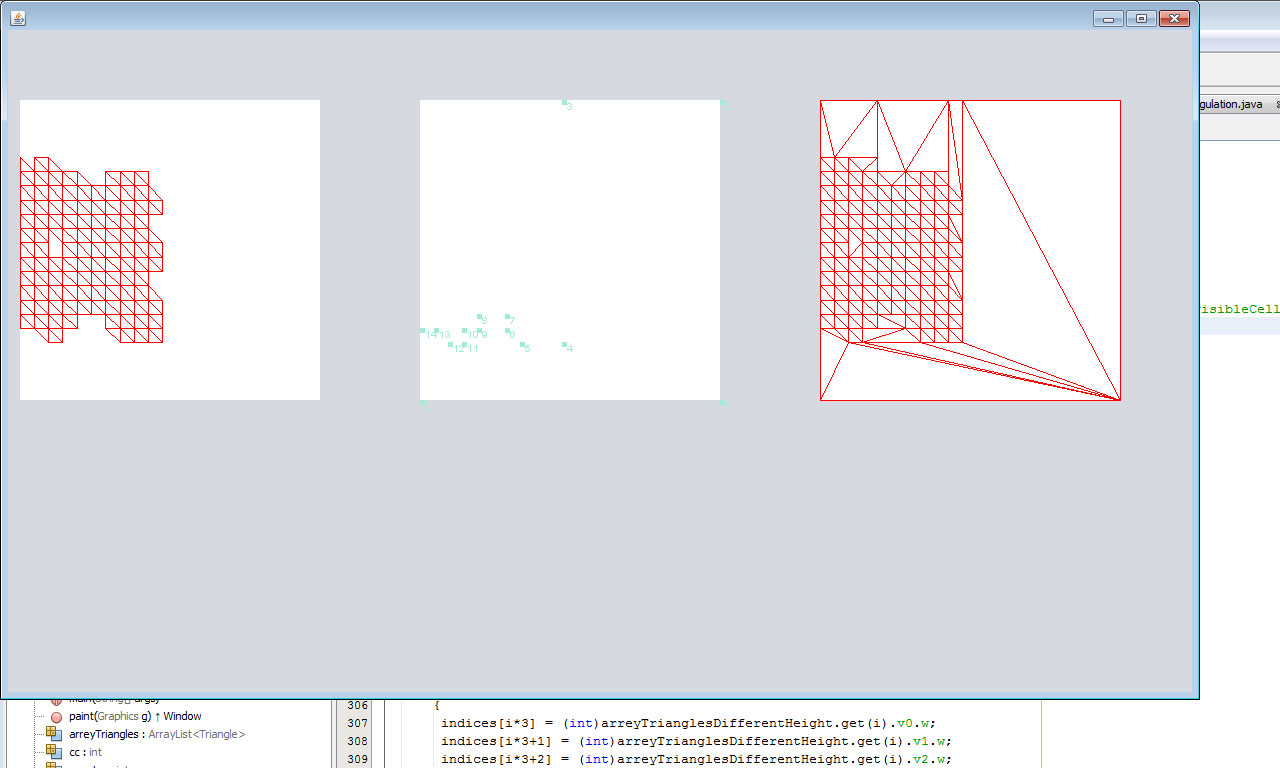
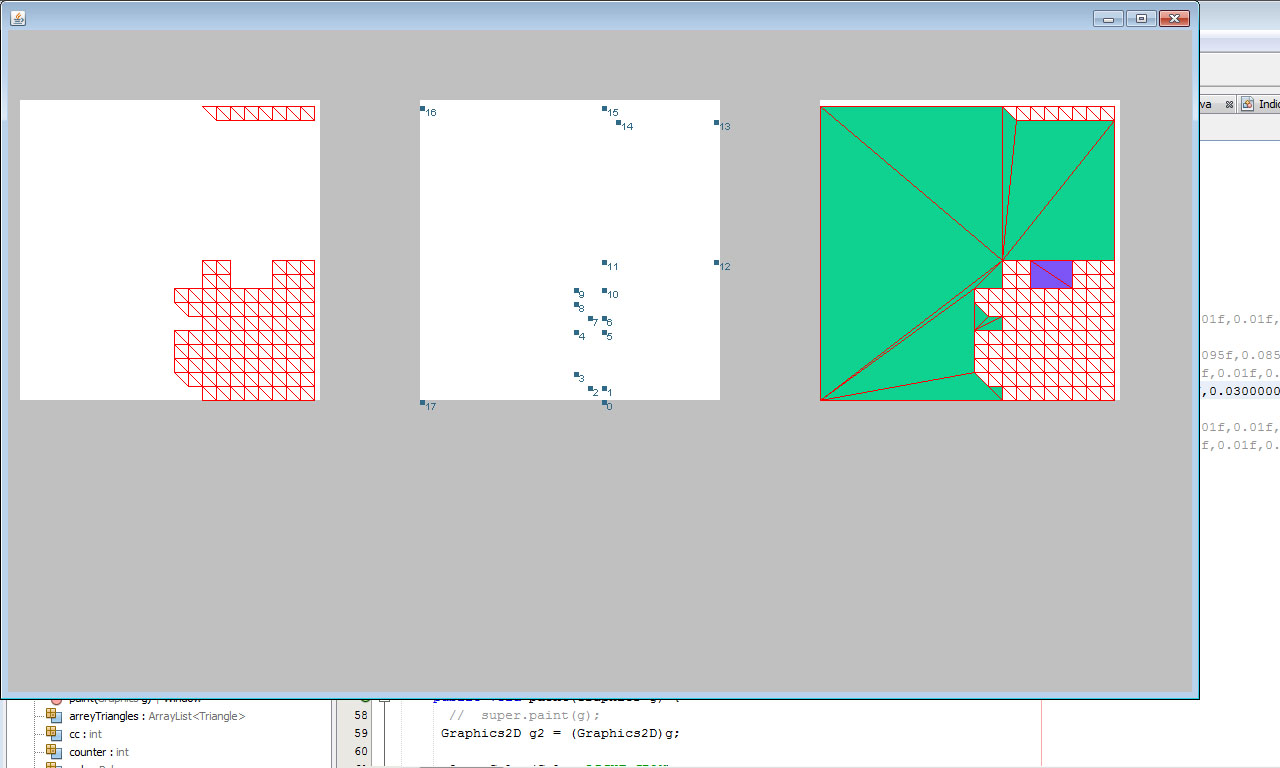
Tudo saiu bem:

Mas no final, fiquei chateado com o resultado. O algoritmo que desenvolvi proporcionou um aumento tangível no desempenho ao renderizar uma cena, já que o número de polígonos em média foi reduzido de 60 a 70%. Mas, ao mesmo tempo, a geração de cartões começou a ocorrer 10 vezes mais lenta. O algoritmo acabou consumindo muito tempo.
Demorou três dias para considerar uma versão leve do algoritmo para otimizar a malha poligonal da paisagem, o que deu os seguintes resultados:

Agora, os cálculos de dados para otimização tornaram-se perceptíveis no contexto da geração de mapas, e o número de polígonos diminuiu, em média, de 40 a 50%.
Este artigo é experimental e superficial. Se alguém estiver interessado no tópico de desenvolvimento de jogos, estou pronto para continuar e expandir o artigo com o fantasma de etapas específicas, soluções e planos futuros. Além disso, acho que você estará interessado no tópico de construção de um aplicativo Open GL multiencadeado desenvolvido em Java, sobre o qual tentarei falar no próximo artigo.