Matemáticos provam que polinômios não ajudarão a hackear o RSA

Recentemente, foi publicado material na revista Quanta, na qual o autor falou sobre um fenômeno surpreendente do ponto de vista de leitores inexperientes, comprovado por matemáticos. Sua essência é que quase todos os polinômios de um determinado tipo são irredutíveis, ou seja, não podem ser decompostos. Esta prova é aplicada em muitas áreas da matemática pura. Mas também são boas notícias para um dos pilares da vida moderna - a criptografia digital.

Para armazenamento confiável de informações digitais, a criptografia usando o algoritmo RSA é amplamente usada. Esta é uma versão aprimorada do esquema que até um aluno da sétima série pode criar para trocar mensagens com amigos: a cada letra é atribuído um número, multiplicado por uma chave secreta e pré-acordada. Para descriptografar uma mensagem, apenas divida-a em uma chave secreta.

A criptografia RSA funciona de maneira semelhante. Damos uma explicação muito simplificada. O usuário cria uma mensagem e executa determinadas operações matemáticas, incluindo a multiplicação por um número muito grande (várias centenas de dígitos). A única maneira de descriptografar a mensagem é encontrar fatores simples do resultado *.

A segurança da criptografia RSA é baseada no fato de que a matemática não conhece maneiras rápidas de encontrar fatores primos de números muito grandes. E se a mensagem criptografada não foi planejada para você e você não tem uma chave para descriptografá-la, as tentativas de encontrar essa chave podem levar milhares de anos. Além disso, isso também se aplica aos computadores mais modernos, com a ajuda dos quais ainda não será possível selecionar os fatores simples corretos.

Mas há uma solução alternativa. Cada número pode ser representado como uma equação algébrica única. E, diferentemente da busca por fatores primos de um número, a busca por fatores primos de um polinômio é muito mais fácil. E assim que o polinômio é decomposto em fatores primos, essas informações podem ser usadas para procurar fatores primos do número original.

Aqui está como isso funciona.

Etapa 1: escolha qualquer número cujos fatores principais você precise descobrir. Para simplificar, use o número 15.

Etapa 2: 15 traduz para binário:

1111

Etapa três: essa expressão binária se transforma em um polinômio ao traduzir todos os números binários em coeficientes do polinômio:



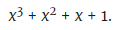
(Nota: esse polinômio é 15 se x = 2. O número 2 é a base do sistema binário.)

Quarto passo: O polinômio é fatorado:



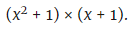Etapa cinco: x = 2 é substituído em cada um desses fatores:



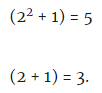Conclusão: 5 e 3 são fatores primos de 15.

Sim, essa é uma maneira excessivamente complicada de encontrar fatores simples de um número pequeno como 15, que são fáceis de descobrir na mente. No entanto, quando se trata de grandes números que consistem em centenas de números, esse método polinomial oferece uma vantagem incrível. Para decompor números primos, algoritmos rápidos não existem. Mas existem algoritmos para decompor grandes polinômios. Portanto, assim que você conseguir transformar um grande número em um grande polinômio, poderá chegar muito perto de encontrar fatores simples do número.

Isso significa que a criptografia RSA está em risco? Na verdade não. E um novo padrão recentemente provado em relação aos polinômios está precisamente conectado a isso.

Os matemáticos Emmanuel Brulya e Peter Varju, da Universidade de Cambridge, provaram que, à medida que os polinômios com coeficientes 0 e 1 se tornam mais longos, a probabilidade de que eles possam ser expandidos diminui. E se o polinômio não puder ser decomposto, ele não poderá ser usado para procurar fatores simples do número que precisa ser calculado.

As evidências de Brull e Varju na verdade sugerem que uma solução alternativa para quebrar a criptografia RSA não leva a lugar algum. Os números muito grandes usados ​​no RSA correspondem a polinômios muito longos. Os cientistas de Cambridge argumentam que é quase impossível encontrar polinômios desse tamanho que possam ser decompostos. Tanto os criptógrafos quanto os matemáticos suspeitam há muito tempo que isso é verdade. No entanto, quando a segurança cibernética mundial depende da impossibilidade de usar alguma técnica matemática, é sempre bom ter provas de que essa técnica realmente não funciona.