Biquaternions

Se você abriu este artigo, provavelmente já ouviu falar sobre quaternions e talvez até os use em seus projetos. Mas é hora de subir para um nível mais alto - para os biquaternions.

Este artigo fornece conceitos básicos sobre biquaternizações e operações com eles. Para uma melhor compreensão do trabalho com biquaternions, é mostrado um exemplo claro em Javascript usando o Canvas.

Biquaternion

O biquaternion é um número hipercomplexo, com uma dimensão 8. Nos artigos e literatura em inglês, eles são chamados de "quaternion duplo", e na literatura em russo também há os nomes "quaternion dual" ou "quaternion complexo".

A principal diferença dos quaternions é que o quaternion descreve a orientação do objeto no espaço, e o biquaternion também descreve a posição do objeto no espaço.

Biquaternion pode ser representado como dois quaternions:

$$

$$\ widetilde {\ textbf {q}} = \ begin {bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix},$$

$$$\ textbf {q} _1$ - a parte real, determina a orientação do objeto no espaço;
$$$\ textbf {q} _2$ - a parte dupla, determina a posição do objeto no espaço.

O biquaternion também é chamado de quaternion complexo, neste caso é representado como um quaternion, cada componente do qual é um número duplo (a não ser confundido com o complexo). Número duplo $$$A = a_1 + \ epsilon a_2$ onde $$$a_1$ e $$$a_2$ São números reais e $$$\ epsilon$ - símbolo de Clifford (complexidade), possuindo a propriedade $$$\ epsilon ^ 2 = 0$ . Não vamos nos aprofundar na matemática, pois estamos mais interessados ​​na parte aplicada; portanto, consideraremos o biquaternion como dois quaternions.

Interpretação geométrica do biquaternion

Por analogia com o quaternion, com o qual você pode definir a orientação do objeto, o biquaternion também pode definir a posição. I.e. O biquaternion define dois valores ao mesmo tempo - a posição e a orientação do objeto no espaço. Se os considerarmos em dinâmica, o biquaternion define duas quantidades - a velocidade linear do movimento e a velocidade angular de rotação do objeto. A figura abaixo mostra o significado geométrico de biquaternion.



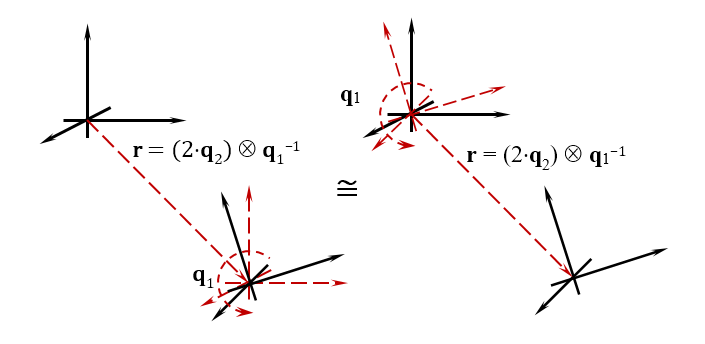
Os desenvolvedores de jogos sabem que, para determinar a posição e a orientação de um objeto no espaço do jogo, são utilizadas matrizes de rotação e de deslocamento e, dependendo da ordem em que você as aplica, o resultado da posição final do objeto é diferente. Para aqueles que estão acostumados a dividir o movimento em operações separadas, aceite a regra para trabalhar com biquaterniões: primeiro movemos o objeto e depois o rotacionamos. De fato, você está descrevendo esses dois movimentos com um único número, embora um hipercomplexo complexo.

Características escalares

Considere as principais características escalares. Aqui é necessário prestar atenção ao fato de que eles retornam não números reais comuns, mas duplos.

1. A norma do biquaternion

$$

$$\ | \ widetilde {\ textbf {q}} \ | = \ | \ textbf {q} _1 \ | + \ epsilon (q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2)$$

2. Módulo Biquaternion

$$

$$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1 |}$$

Operações básicas

Considere as operações básicas de trabalho com biquaternions. Como você pode ver, eles são muito semelhantes a operações semelhantes com quaternions.

1. Emparelhamento Biquaternion

$$

$$\ widetilde {\ textbf {q}} ^ * = \ begin {bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$$

2. Adição e subtração de biquaterniões

$$

$$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ pm \ textbf {p} _2 \ end {bmatrix}$$

A adição e subtração de biquaternions é comutativa (os termos podem ser trocados).

3. Multiplicação do número real por biquaternion

$$

$$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ begin {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$$

4. Multiplicação Biquaternion

$$

$$\ widetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ otimes \ textbf {p} _1 \\ \ textbf {q} _1 \ otimas \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$$

A multiplicação de biquaterniões não é comutativa (com uma mudança na ordem dos fatores, o resultado da multiplicação de biquatiões é diferente).

Esta operação é uma das principais quando se trabalha com biquatérnions e possui um significado físico, ou seja, o resultado da multiplicação do biquaternion é a operação de adicionar as rotações e movimentos lineares de dois biquaternions.

5. Batismo reverso

$$

$$\ widetilde {\ textbf {q}} ^ {- 1} = \ frac {\ widetilde {\ textbf {q}} ^ *} {\ | \ widetilde {\ textbf {q}} \ |}$$

Determinação do biquaternio através de ângulos de orientação e vetor de posição

Primeiro, definimos os sistemas de coordenadas nos quais consideraremos a orientação e a posição do objeto no espaço. Isso deve ser feito para especificar a parte real do biquaternion (quaternion de orientação), cuja sequência de rotação afeta o quaternion resultante dos ângulos de orientação. Aqui seremos guiados por ângulos de avião - guinada $$$\ psi$ arremesso $$$\ vartheta$ e rolar $$$\ gama$ .

Defina o sistema de coordenadas da base. Imagine que você está parado na superfície da Terra e olhando na direção do norte.

Ponto O _o - a origem do sistema de coordenadas, localizado no ponto de origem do objeto.
O eixo O _o Y _g - é direcionado verticalmente para cima e é oposto à direção do vetor de gravidade.
O eixo O _o X _g - é direcionado para o norte, ao longo da tangente do meridiano local.
Eixo O _o Z _g - complementa o sistema para a direita e é direcionado para a direita, em direção ao leste.

O segundo sistema de coordenadas está conectado. Imagine, por exemplo, um avião ou outro objeto.
Ponto O - a origem do sistema de coordenadas, via de regra, está localizada no ponto do centro de massa do objeto.
Eixo OY - direcionado verticalmente para cima e perpendicular ao plano horizontal do objeto.
Axis OX - direcionado para o ponto frontal do objeto.
Eixo OZ - complementa o sistema à direita.

A posição do objeto no espaço é determinada pelo vetor de raio da origem (ponto O ) do sistema de coordenadas associado em relação ao sistema de coordenadas da base fixa. A orientação do sistema de coordenadas associado em relação à base é determinada por três turnos sucessivos:

ângulo da guinada $$$\ psi$ - rotação em torno do eixo OY ,
ângulo de inclinação $$$\ vartheta$ - rotação em torno do eixo OZ ,
ângulo de rolagem $$$\ gama$ - rotação ao redor do eixo OX .

Para a determinação inicial do biquaternion, você deve especificar as partes real e dupla do biquaternion. A orientação e a posição do objeto são definidas em relação a um determinado sistema de coordenadas base usando ângulos de orientação $$$\ psi, \ vartheta, \ gama$ e vetor de posição do centro de massa $$$r = (r_x, r_y, r_z) ^ T$ .

A parte real $$$\ textbf {q} _1$ pode ser definido usando a fórmula:

$$

$$\ textbf {q} _1 = \ begin {bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} e - & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ cos \ frac { \ vartheta} {2} \ sin \ frac {\ gama} {2} & + & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} e + & \ sin \ frac {\ psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} e - & \ sin \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \ end {bmatrix}$$

Observe que, se você tiver uma sequência de rotação diferente, as expressões também serão diferentes.

Parte dupla $$$\ textbf {q} _2$ definido pela expressão:

$$

$$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$$

Cálculo dos ângulos de orientação e vetor de posição do biquatérion Transformação inversa

Os ângulos de orientação podem ser calculados a partir da parte real do biquíni. $$$\ textbf {q} _1$ :

$$

$$\ psi = \ arctan {\ frac {2 (q_0 q_2 - q_1 q_3)} {q_0 ^ 2 + q_1 ^ 2 - q_2 ^ 2 - q_3 ^ 2}}$$

$$

$$\ vartheta = \ arcsin {(2 (q_1 q_2 + q_0 q_3))}$$

$$

$$\ gamma = \ arctan {\ frac {2 (q_0 q_1 - q_2 q_3)} {q_0 ^ 2 - q_1 ^ 2 + q_2 ^ 2 - q_3 ^ 2}}$$

A posição do objeto é determinada pela expressão:

$$

$$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {- 1}$$

o resultado é um vetor em forma de quaternário $$$\ textbf {r} = (0, r_x, r_y, r_z) ^ T$

Gire e mova o biquaternion de vetor

Uma das grandes propriedades dos biquatérnions é a rotação e o movimento de um vetor de um sistema de coordenadas para outro. Seja O _o X _g Y _g Z _g um sistema de coordenadas de base fixo e OXYZ seja o sistema de coordenadas conectado do objeto. Em seguida, a orientação e a posição do objeto em relação ao sistema de coordenadas base podem ser especificadas pelo biquaternion $$$\ widetilde {\ textbf {q}}$ . Se um vetor for especificado $$$\ textbf {r}$ em um sistema de coordenadas conectado, você pode obter um vetor $$$\ textbf {r} _0$ no sistema de coordenadas base usando a fórmula:

$$

$$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {- 1}$$

e de volta:

$$

$$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {- 1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}}$$

onde $$$\ textbf {r}$ É um vetor em forma de biquíni, $$$\ textbf {r} = (1, 0, 0, 0, 0, 0, r_x, r_y, r_z)$

Biblioteca JavaScript Biquaternion

Todas as operações acima com biquaternions são implementadas na biblioteca javascript, dependendo das suas tarefas, elas podem ser implementadas em outras linguagens de programação. As principais funções do trabalho com biquaternions:

Função	Descrição do produto
DualQuaternion.dq	Corpo biquaternário como uma matriz de 8 números
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)	Um construtor que define um biquíni, especificando todos os oito números
DualQuaternion.fromEulerVector(psi, theta, gamma, v)	Obter biquaternion definindo a orientação do objeto com ângulos de Euler e o vetor de posição do objeto
DualQuaternion.getEulerVector()	Obter ângulos de Euler e vetor de posição do biquaternion
DualQuaternion.getVector()	Obter vetor de posição de biquaternion
DualQuaternion.getReal()	Obter a parte real do biquaternion (determina a orientação do objeto no espaço)
DualQuaternion.getDual()	Obter a parte dupla do biquaternion (determina a posição do objeto no espaço)
DualQuaternion.norm()	Obter a norma biquaternion como um número duplo
DualQuaternion.mod()	Obtenha o módulo biquaternion como um número duplo
DualQuaternion.conjugate()	Obter o biquaternion conjugado
DualQuaternion.inverse()	Obter Biquaternion reverso
DualQuaternion.mul(DQ2)	Multiplicação biquaternion
DualQuaternion.toString()	Converter biquaternion em uma cadeia de caracteres, por exemplo, para saída no console de depuração

Um exemplo de trabalho com biquaternions

Para uma melhor compreensão dos conceitos básicos do uso de biquaternions como exemplo, considere um pequeno jogo. A área retangular é definida - o mapa. Um navio flutuando em um mapa com uma pistola rotativa montada no mapa. Aqui é necessário levar em consideração que, para o navio, o sistema de coordenadas básicas é o sistema de coordenadas do mapa, e para a arma o sistema de coordenadas básicas é o navio. Todos os objetos são desenhados no sistema de coordenadas do mapa e aqui será interessante ver como é possível ir do sistema de coordenadas da pistola para o sistema de coordenadas do mapa usando a propriedade de multiplicação do biquaternion. O movimento do navio é controlado pelas teclas W, A, S, D. A direção da arma é definida pelo cursor do mouse.



O navio e a arma são descritos por duas classes: Ship e Gun . No construtor da classe de navio, sua forma na forma de pontos de biquíni, a orientação inicial e a posição no mapa na forma de this.dq_pos biquaternion são this.dq_pos .

Também são fornecidos incrementos de biquaternidade para o controle do navio. Ao se mover para frente e para trás (teclas W, S), apenas a parte dupla do biquíni é alterada e, ao controlar a esquerda e a direita (teclas A, D), a parte real e dupla do biquaternion muda, o que define o ângulo de rotação.

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); //   this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); //      this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; }; 

Na própria classe, há apenas uma função para renderizar a Ship.draw() . Preste atenção à aplicação da operação de biquatérion de multiplicar cada ponto do navio pelo biquatérion da posição e orientação atual do navio.

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** *   */ 'draw': function() { //         v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } }; 

No construtor da classe de armas, sua forma na forma de pontos de biquíni é especificada. A arma será exibida como uma linha. A orientação e posição iniciais no navio são definidas pelo this.dq_pos biquaternion. Além disso, a ligação ao navio em que está instalado também é definida. A pistola no navio só pode girar, então o biquaternion aumenta quando o controle da arma muda apenas a parte real do biquaternion, que define o ângulo de rotação. Neste exemplo, o implemento é guiado pelo cursor do mouse, de modo que a rotação da pistola ocorrerá instantaneamente.

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; //     this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); //   this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); //     this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; }; 

Na classe gun, apenas uma função de renderizar Ship.draw() também Ship.draw() implementada. A arma é exibida como uma linha, que é definida por dois pontos this.dq_backward e this.dq_forward . Para determinar as coordenadas dos pontos da pistola, é utilizada a operação de multiplicação do biquaternion.

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** *   */ 'draw': function() { //     v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } }; 

O processamento de controle de navios e armas é implementado por meio de eventos. Quatro variáveis leftPressed, upPressed, rightPressed, downPressed , que são processadas no loop principal do programa, são responsáveis ​​por pressionar e liberar as teclas de controle do navio.

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); //     function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } //  S } //     function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } //  S } 

Uma das funções mais interessantes, do ponto de vista do uso de operações de biquíni, é controlar a arma do navio na direção do ponteiro do mouse. Primeiro, as coordenadas do ponteiro do mouse são determinadas no dq_mouse_pos biquaternion. Em seguida, o biquatião da posição do mouse em relação ao navio é calculado usando a multiplicação do biquatino. O biquatião do navio é retirado do dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); do mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(Nota: as operações de multiplicação sequencial de biquíni são lidas da direita para a esquerda). E, finalmente, o ângulo entre os vetores da ferramenta e o mouse é determinado. O ponto inicial da arma gun_1.dq_backward recebe o valor recebido.

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; //           if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { //    dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); //      //  .       //     // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); //       q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } } 

No corpo principal do programa, os objetos do navio e das armas ship_1 e gun_1 , as informações de depuração são exibidas e o processamento de controle do navio é realizado.

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); //   if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw(); 

O link para o arquivo contém o código completo das bibliotecas para trabalhar com quaternions e biquaternions, o próprio script do programa e o arquivo index.html, que pode ser aberto localmente no navegador para executar o exemplo acima.

Um exemplo de trabalho com biquaternions

Conclusão

Você pode ter uma pergunta: por que usar um aparato matemático tão complexo quando se pode conviver com ferramentas padrão para mover e girar objetos? Uma das principais vantagens é que a forma de escrever biquaternion é mais computacionalmente eficiente, pois todas as operações com biquaternions após a expansão das expressões são lineares. Este vídeo, Skinning geométrico com mistura aproximada de quaternário duplo, mostra o quão mais eficientes são os cálculos do biquaternion do que outros métodos.

Eu peguei principalmente informações sobre o uso de biquaternions de fontes inglesas.
Da literatura doméstica, posso aconselhar dois livros:

1. Chelnokov Yuri Nikolaevich. Modelos e métodos de Quaternion e biquaternion de mecânica dos sólidos e suas aplicações. Geometria e cinemática do movimento. - trabalho teórico monumental.
2. Gordeev Vadim Nikolaevich. Quaternions e biquaternions com aplicações em geometria e mecânica. - É escrito em uma linguagem mais compreensível e mostra aplicações nas tarefas de modelar estruturas espaciais curvas.