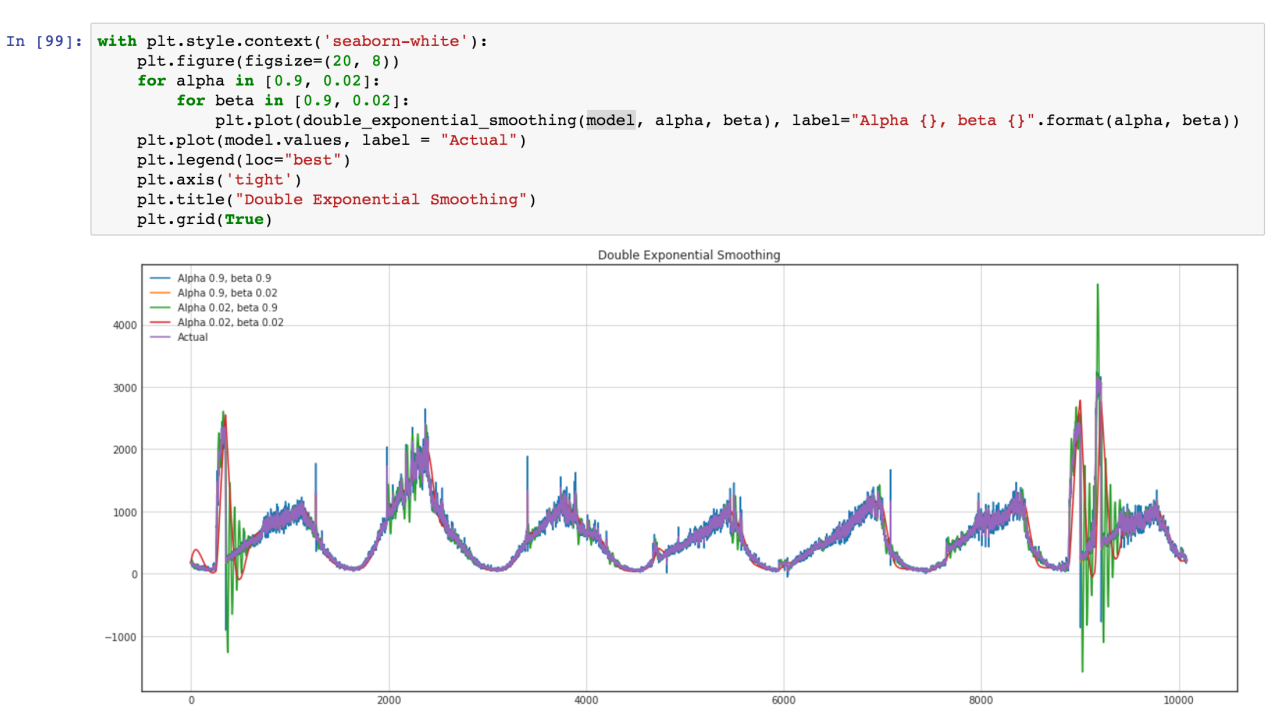
Este é um pequeno artigo sobre como entender as séries temporais e as principais características por trás disso.
Declaração do Problema
Temos dados de séries temporais com regularidade diária e semanal. Queremos descobrir como modelar esses dados da maneira ideal.

Analisando séries temporais
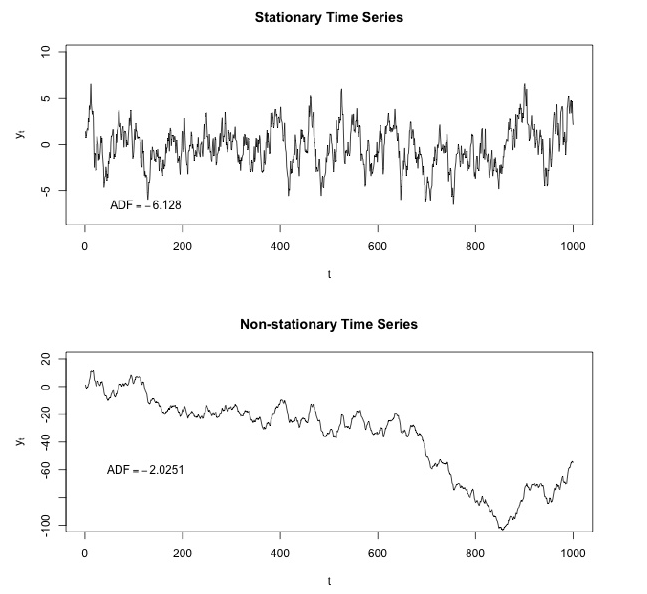
Uma das características importantes das séries temporais é a estacionariedade.
Em matemática e estatística, um processo estacionário (também conhecido como processo estacionário estrito) ou processo estacionário forte é um processo estocástico cuja distribuição de probabilidade conjunta não muda quando deslocada no tempo.
Consequentemente, parâmetros como média e variância, se estiverem presentes, também não mudam com o tempo. Como a estacionariedade é uma suposição subjacente a muitos procedimentos estatísticos usados na análise de séries temporais, dados não estacionários são frequentemente transformados para se tornarem estacionários.
A causa mais comum de violação da estacionariedade são as tendências em média, que podem ser devidas à presença de uma raiz unitária ou de uma tendência determinística. No primeiro caso de uma raiz unitária, os choques estocásticos têm efeitos permanentes e o processo não reverte a média. No último caso de uma tendência determinística, o processo é chamado de processo estacionário de tendência, e os choques estocásticos têm apenas efeitos transitórios que revertem a média (ou seja, a média retorna à sua média de longo prazo, que muda determinística ao longo do tempo de acordo com a tendência).
Exemplos de processos estacionários versus processos não estacionários
Linha de tendência
Dispersão
O ruído branco é um processo estacionário estocástico que pode ser descrito usando dois parâmetros: média e dispersão (variância). Em tempo discreto, o ruído branco é um sinal discreto cujas amostras são consideradas como uma sequência de variáveis aleatórias serialmente não correlacionadas com média zero e variância finita.
Se fizermos projeção no eixo y, podemos ver a distribuição normal. O ruído branco é um processo gaussiano no tempo.
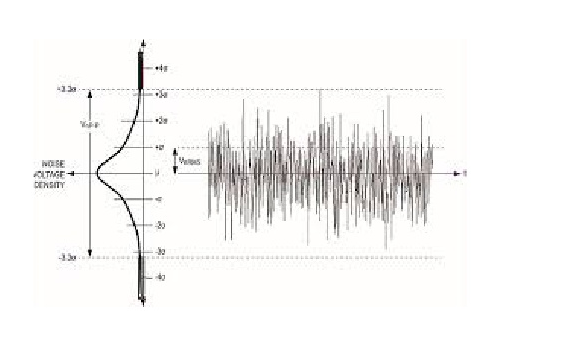
Na teoria da probabilidade, a distribuição normal (ou gaussiana) é uma distribuição de probabilidade contínua muito comum. Distribuições normais são importantes em estatística e são frequentemente usadas nas ciências naturais e sociais para representar variáveis aleatórias com valor real cujas distribuições não são conhecidas. A distribuição normal é útil devido ao teorema do limite central. Em sua forma mais geral, sob algumas condições (que incluem variância finita), afirma que as médias de amostras de observações de variáveis aleatórias extraídas independentemente de distribuições independentes convergem na distribuição para o normal, ou seja, normalmente são distribuídas quando o número de observações é suficientemente grande. Quantidades físicas que se espera que sejam a soma de muitos processos independentes (como erros de medição) geralmente têm distribuições quase normais. Além disso, muitos resultados e métodos (como propagação da incerteza e ajuste dos parâmetros dos mínimos quadrados) podem ser derivados analiticamente de forma explícita quando as variáveis relevantes são normalmente distribuídas.
Suponha que nossos dados tenham alguma tendência. Os picos em torno dele se devem a muitos fatores aleatórios, que afetam nossos dados. Por exemplo, a quantidade de solicitações atendidas é descrita usando essa abordagem muito bem. Coleta de lixo, falhas de cache, paginação pelo SO, muitas coisas afetam o tempo específico da resposta atendida. Vamos tirar uma fatia de meia hora de nossos dados, de 8 a 27 de 2017, das 12h às 12h30. Podemos ver que esses dados têm uma tendência e algumas oscilações
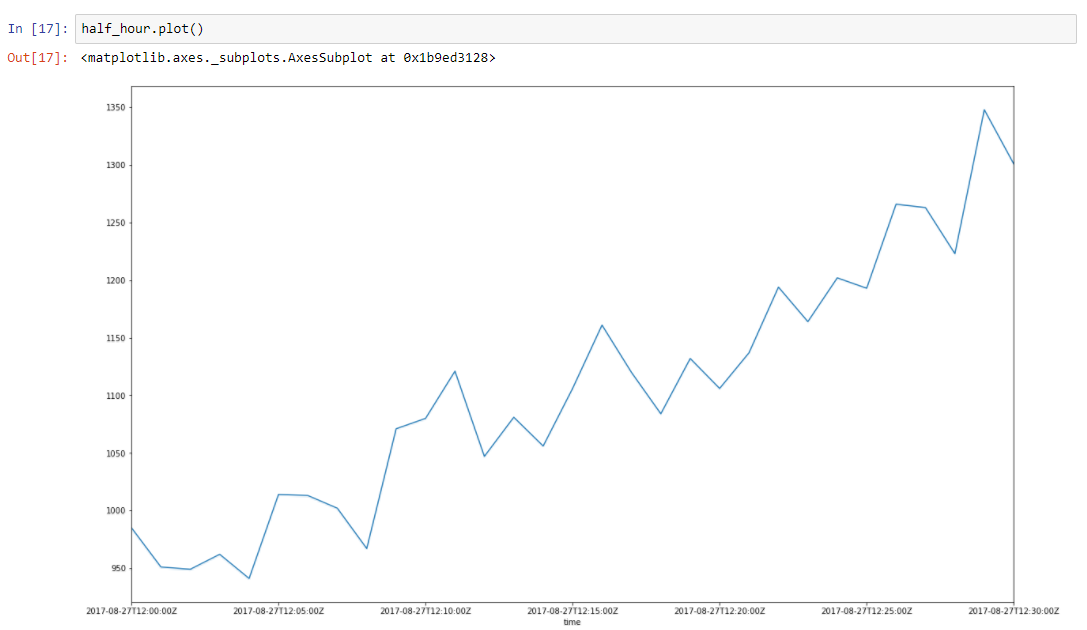
Vamos construir uma linha de regressão para definir a inclinação dessa linha de tendência.
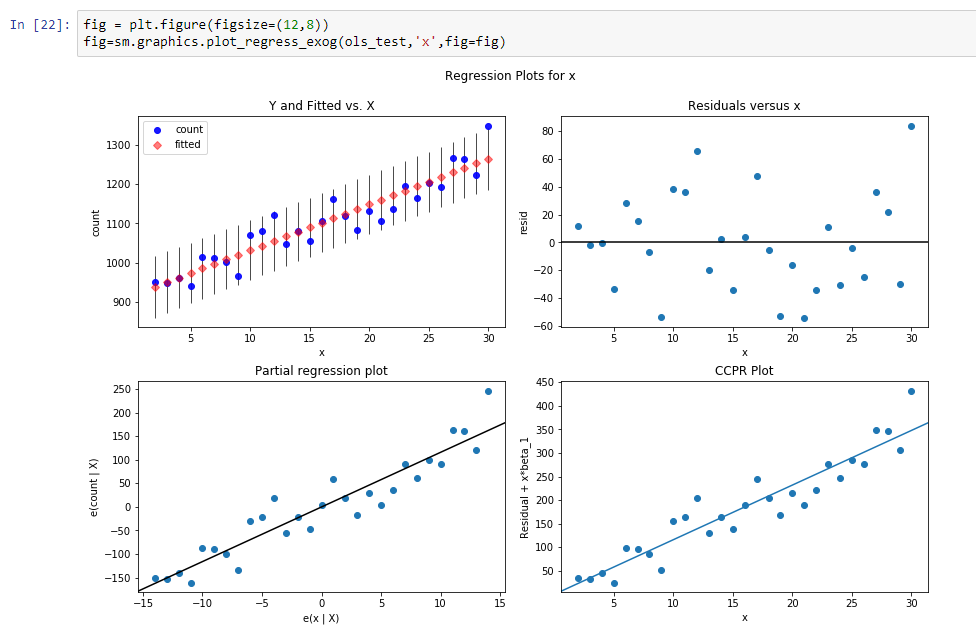
Os resultados dessa regressão são:
const 916.269951dy / dx 11.599507Resultados significa que const é um nível para esta linha de tendência e dy / dx é uma linha de inclinação que define a velocidade com que o nível cresce de acordo com o tempo.
Então, na verdade, reduzimos a dimensão dos dados de 31 parâmetros para 2 parâmetros. Se subtrairmos de nossos dados iniciais nossos valores de função de regressão, veremos processo, que parece um processo estocástico estacionário.
Então, após a subtração, podemos ver que a tendência desapareceu e podemos assumir que o processo é estocástico nesse intervalo. Mas como podemos ter certeza.

Vamos fazer o
teste Dickey - Fuller .
Dickey - Fuller testa a hipótese nula de que as séries temporais têm raiz e também são estacionárias ou rejeitam essa hipótese. Se fizermos o teste Dickey-Fuller em nossa fatia inicial, obteremos
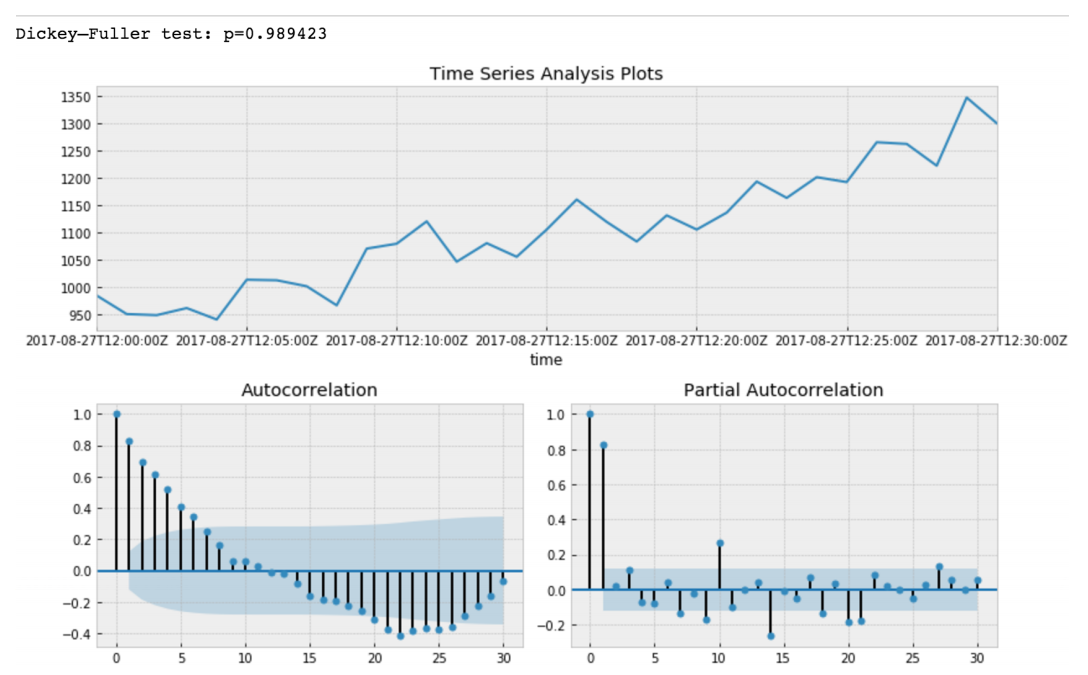
O valor do teste Dickey-Fuller rejeita a hipótese nula com uma forte confiança. Portanto, nossa fatia de séries temporais é não estacionária. E podemos ver que a função de autocorrelação mostra autocorrelações ocultas.
Após subtração do nosso modelo de regressão dos dados iniciais.

Aqui podemos ver que o valor do teste Dickey-Fuller é realmente pequeno e não rejeita uma hipótese nula sobre a não estacionariedade da fatia da série temporal. Também a função de autocorrelação parece bem.
Assim, fizemos algumas transformações em nossos dados e podemos rotacioná-los de acordo com a inclinação de nossa linha de tendência.
Regressão segmentada dos dados
A regressão segmentada , também conhecida como
regressão por partes ou "regressão em bastão", é um método na análise de regressão em que a variável independente é particionada em intervalos e um segmento de linha separado é adequado para cada intervalo. A análise de regressão segmentada também pode ser realizada em dados multivariados particionando as várias variáveis independentes. A regressão segmentada é útil quando as variáveis independentes, agrupadas em grupos diferentes, exibem relações diferentes entre as variáveis nessas regiões. Os limites entre os segmentos são pontos de interrupção.
Na verdade, nossa inclinação é um derivado discreto de nossas séries temporais não estacionárias, devido ao intervalo constante de nossos pontos métricos que não podemos levar em consideração dx. Portanto, podemos aproximar nossos dados como uma função composta que calculou usando derivadas discretas das tendências de regressão de séries temporais.

Acima, há uma fatia de dados de 26–08–2017, de 00.00 a 08.00
Parece que existe uma autocorrelação linear para cada fatia e, se encontrarmos uma linha de regressão para cada fatia, podemos construir um modelo de nossas fatias de tempo usando suposições que fizemos.
Como resultado, teremos dados que são descritos usando uma quantidade mínima de parâmetros que é favorável devido a uma melhor generalização. A dimensão Vapnik - Chervonenkis deve ser a menor possível para uma boa generalização.
Na teoria Vapnik - Chervonenkis, a dimensão VC (para a dimensão Vapnik - Chervonenkis) é uma medida da capacidade (complexidade, poder expressivo, riqueza ou flexibilidade) de um espaço de funções que pode ser aprendido por um algoritmo de classificação estatística. É definida como a cardinalidade do maior conjunto de pontos que o algoritmo pode quebrar. Foi originalmente definido por Vladimir Vapnik e Alexey Chervonenkis.
Formalmente, a capacidade de um modelo de classificação está relacionada ao quão complicado ele pode ser. Por exemplo, considere o limiar de um polinômio de alto grau: se o polinômio for avaliado acima de zero, esse ponto será classificado como positivo, caso contrário, como negativo. Um polinômio de alto grau pode ser confuso, para que ele se encaixe bem em um determinado conjunto de pontos de treinamento. Mas pode-se esperar que o classificador cometa erros em outros pontos, porque é muito complicado. Esse polinômio tem uma alta capacidade. Uma alternativa muito mais simples é limitar uma função linear. Esta função pode não se encaixar bem no conjunto de treinamento, pois possui baixa capacidade.
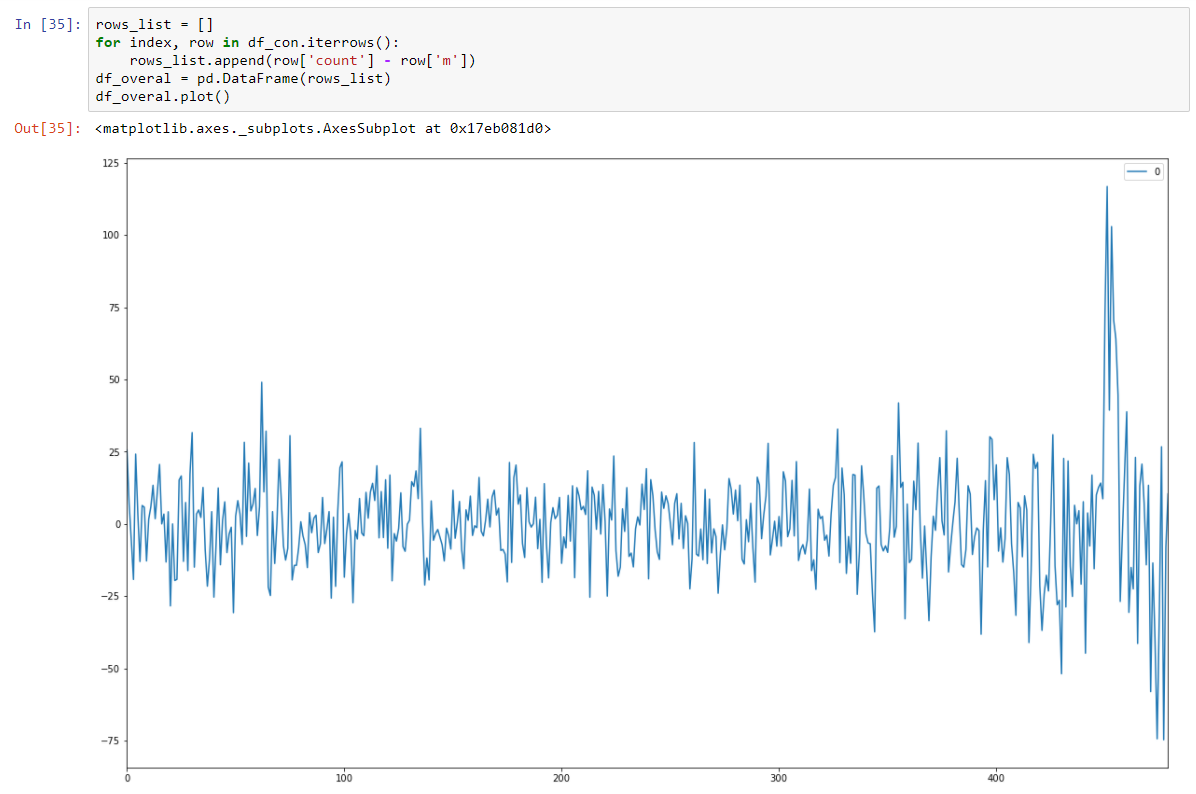
Portanto, como resultado, aproximamos nossas fatias de horas usando regressão segmentada.
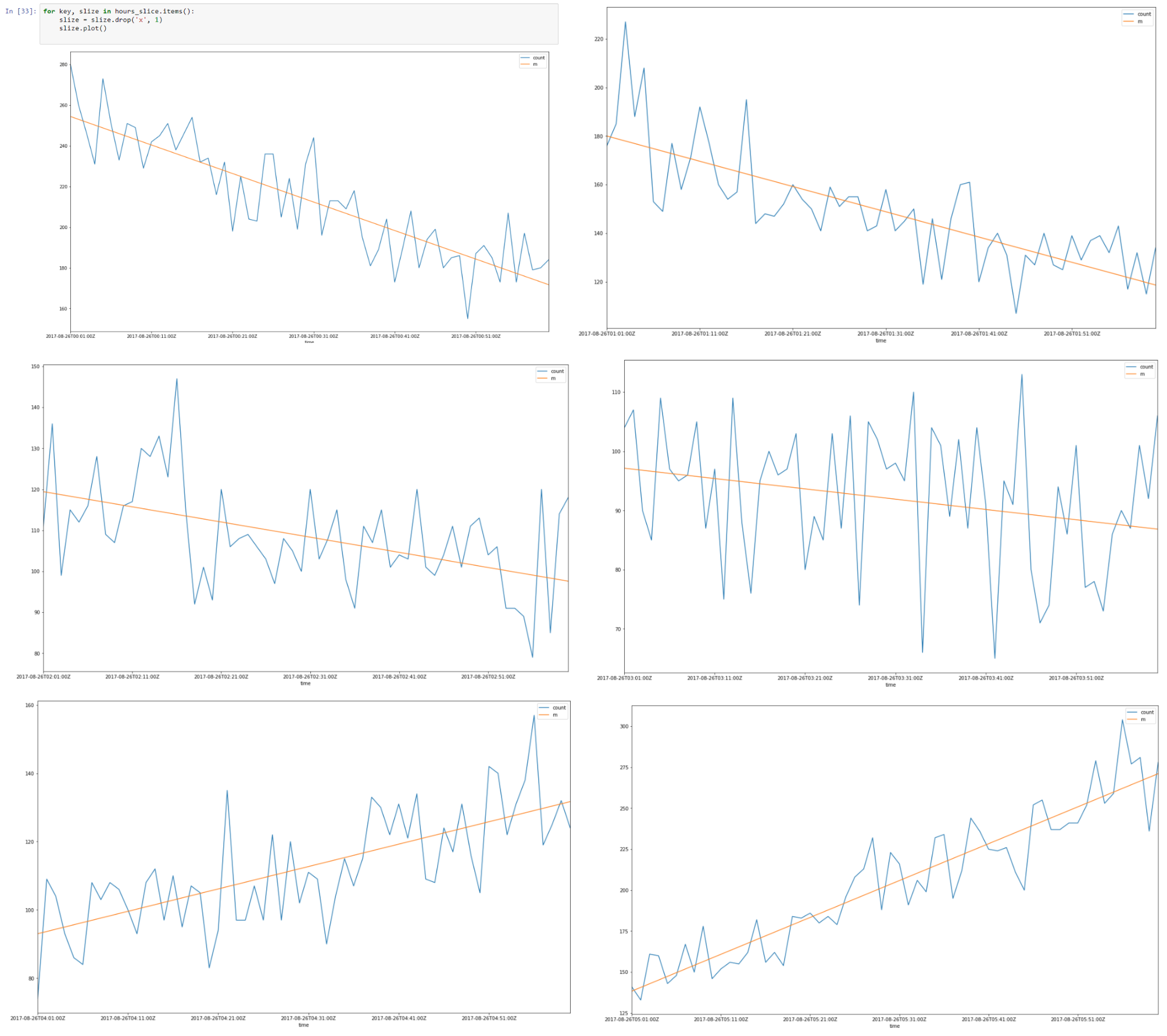
Reunindo todas as fatias de 8 horas

E torne-o estacionário estocástico subtraindo o modelo de regressão.
E nosso teste Dickey-Fuller em estacionário está mostrando com forte confiança que transformamos nossos dados em séries estacionárias.
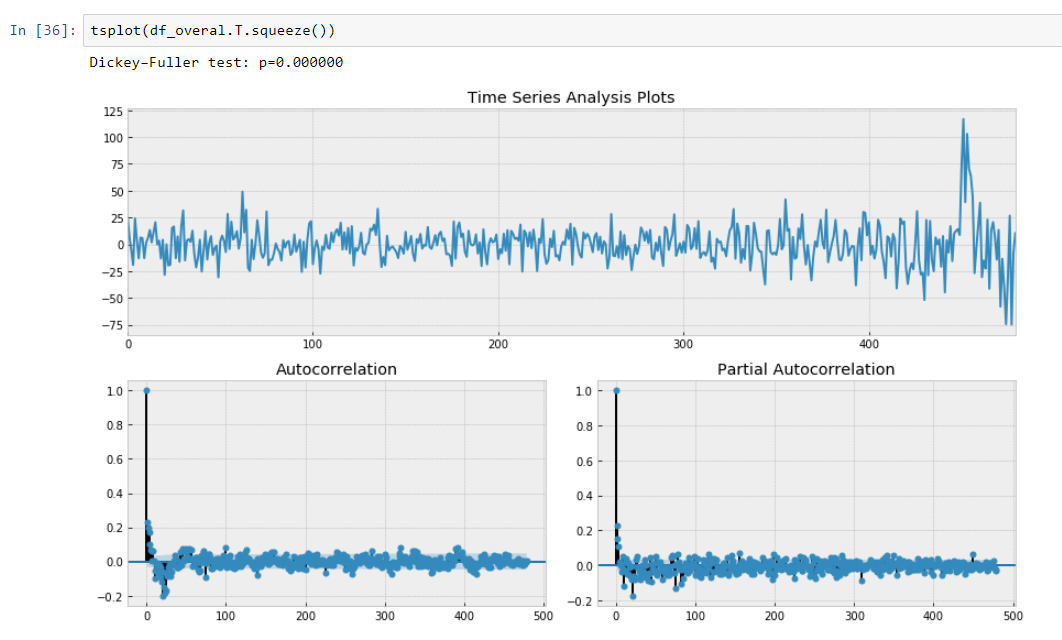
Portanto, temos um modelo de previsão que descreve nossos dados de séries temporais. Reduzimos a dimensionalidade dos nossos dados em 15/30 vezes menor!
Na verdade, devemos retornar a média da previsão de nosso modelo e transformá-la novamente usando nível e inclinação para uma fatia específica. Minimizará a soma dos erros quadráticos para a previsão de nossos modelos.
Mas também devemos armazenar a variação, porque o aumento da variação pode levar à presença de novos fatores desconhecidos e, como sabemos pelo domínio, é assim.
Portanto, mudanças rápidas na variação também devem ser alertadas.
Também queremos usar o modelo ARIMA, mas uma abordagem mais geral é melhor, e planejamos comparar esse modelo e o ARIMA padrão para obter melhores resultados. Vamos ver a nossa série temporal (Verde são variações de variação em valores extremos)