Lembrete
Olá Habr! Trago à sua atenção outra tradução do meu novo artigo da
mídia .
Da última vez (
primeiro artigo ) (
Habr ), criamos um agente usando a tecnologia Q-Learning, que realiza transações em séries temporais simuladas e reais de troca e tentamos verificar se essa área de tarefas é adequada para o aprendizado reforçado.
Desta vez, adicionaremos uma camada LSTM para levar em conta as dependências de tempo da trajetória e recompensar a engenharia de modelagem com base nas apresentações.
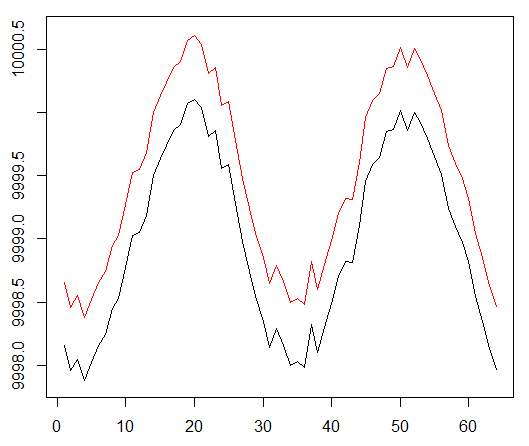
Deixe-me lembrá-lo que, para verificar o conceito, usamos os seguintes dados sintéticos:
Dados sintéticos: seno com ruído branco.
A função seno foi o primeiro ponto de partida. Duas curvas simulam o preço de compra e venda de um ativo, em que o spread é o custo mínimo da transação.
No entanto, desta vez queremos complicar essa tarefa simples estendendo o caminho da atribuição de crédito:
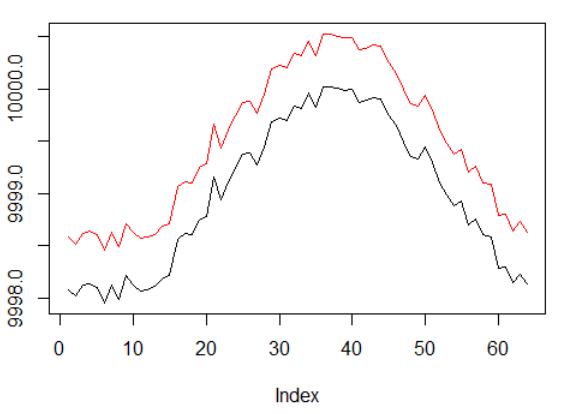
Dados sintéticos: seno com ruído branco.
A fase sinusal foi duplicada.
Isso significa que as recompensas esparsas que usamos devem se espalhar por trajetórias mais longas. Além disso, reduzimos significativamente a probabilidade de receber uma recompensa positiva, pois o agente teve que executar uma sequência de ações corretas duas vezes mais para superar os custos de transação. Ambos os fatores complicam bastante a tarefa da RL, mesmo em condições simples como uma onda senoidal.
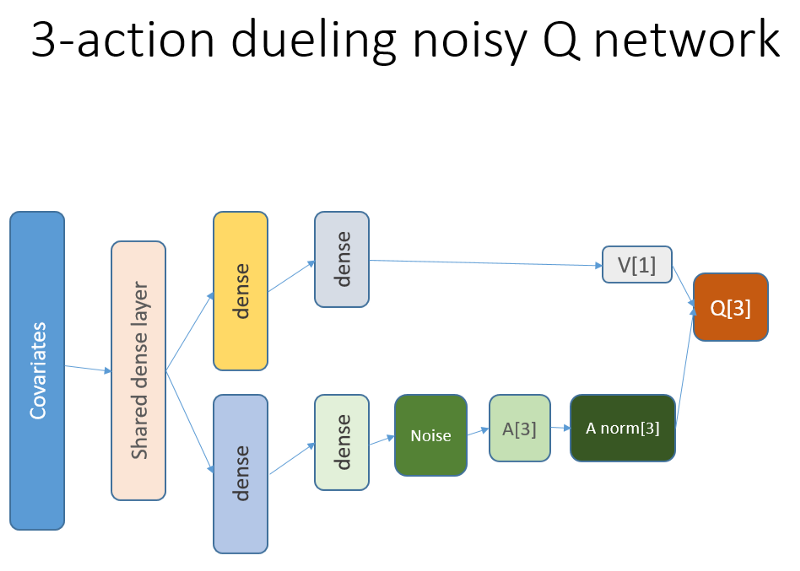
Além disso, lembramos que usamos essa arquitetura de rede neural:
O que foi adicionado e por quê
Lstm
Antes de tudo, queríamos dar ao agente mais entendimento da dinâmica das mudanças dentro da trajetória. Simplificando, o agente deve entender melhor seu próprio comportamento: o que ele fez agora e por algum tempo no passado e como a distribuição das ações do Estado, bem como as recompensas recebidas, se desenvolveram. O uso de uma camada de recorrência pode resolver exatamente esse problema. Bem-vindo à nova arquitetura usada para lançar um novo conjunto de experiências:

Por favor, note que eu melhorei ligeiramente a descrição. A única diferença do NN antigo é a primeira camada LSTM oculta, em vez de uma camada totalmente ligada.
Observe que, com o LSTM em funcionamento, precisamos alterar a seleção de exemplos da reprodução da experiência para treinamento: agora precisamos de sequências de transição em vez de exemplos separados. Veja como funciona (este é um dos algoritmos). Usamos amostragem pontual antes:

O esquema fictício do buffer de reprodução.
Usamos esse esquema com LSTM:

Agora as seqüências são selecionadas (cujo comprimento especificamos empiricamente).
Como antes, e agora a amostra é regulada por um algoritmo de prioridade baseado em erros de aprendizado temporal-temporal.
O nível de recorrência LSTM permite a disseminação direta de informações de séries temporais para interceptar um sinal adicional oculto em atrasos anteriores. Nossa série temporal é um tensor bidimensional com tamanho: o comprimento da sequência na representação de nossa ação estatal.
Apresentações
A engenharia premiada, PBRS (Potential Based Reward Shaping), com base no potencial, é uma ferramenta poderosa que permite aumentar a velocidade, a estabilidade e não violar a otimização do processo de pesquisa de políticas para resolver nosso ambiente. Eu recomendo a leitura de pelo menos este documento original sobre o tópico:
people.eecs.berkeley.edu/~russell/papers/ml99-shaping.psPotencial determina quão bem nosso estado atual é relativo ao estado de destino que queremos inserir. Uma visão esquemática de como isso funciona:

Existem opções e dificuldades que você pode entender após tentativa e erro e omitimos esses detalhes, deixando você com sua lição de casa.
Vale mencionar mais uma coisa: a PBRS pode ser justificada usando apresentações, que são uma forma de conhecimento especializado (ou simulado) sobre o comportamento
quase ideal do agente no ambiente. Existe uma maneira de encontrar essas apresentações para nossa tarefa usando esquemas de otimização. Omitimos os detalhes da pesquisa.
A recompensa potencial assume a seguinte forma (equação 1):
r '= r + gama * F (s') - F (s)
onde F é o potencial do estado er é a recompensa inicial, gama é o fator de desconto (0: 1).
Com esses pensamentos, passamos à codificação.Implementação em R
Aqui está o código de rede neural baseado na API Keras:
Depurando sua decisão em sua consciência ...
Resultados e Comparação
Vamos mergulhar nos resultados finais.
Nota: todos os resultados são estimativas pontuais e podem diferir em várias execuções com diferentes sementes aleatórias.A comparação inclui:
- versão anterior sem LSTM e apresentações
- LSTM simples de 2 elementos
- LSTM de 4 elementos
- LSTM de 4 células com recompensas PBRS geradas
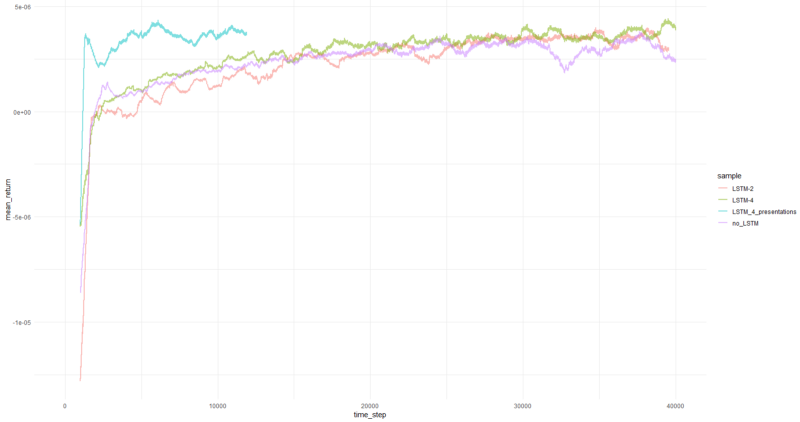
O retorno médio por episódio atingiu em média mais de 1000 episódios.
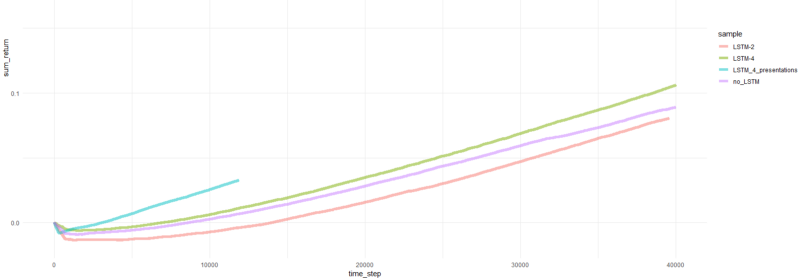
Total de episódios retornados.
Gráficos para o agente mais bem-sucedido:

Desempenho do agente.
Bem, é óbvio que o agente na forma de PBRS converge tão rapidamente e de forma estável em comparação com tentativas anteriores que pode ser aceito como um resultado significativo. A velocidade é cerca de 4-5 vezes maior do que sem apresentações. A estabilidade é maravilhosa.
Quando se trata de usar LSTM, 4 células tiveram desempenho melhor que 2 células. Um LSTM de 2 células teve um desempenho melhor que uma versão não LSTM (no entanto, talvez isso seja uma ilusão de um único experimento).
Palavras finais
Vimos que a recorrência e as recompensas de capacitação ajudam. Eu gostei especialmente de como o PBRS se saiu tão bem.
Não acredite em ninguém que me faça dizer que é fácil criar um agente de RL que converge bem, pois isso é mentira. Cada novo componente adicionado ao sistema o torna potencialmente menos estável e requer muita configuração e depuração.
No entanto, há evidências claras de que a solução do problema pode ser melhorada simplesmente melhorando os métodos utilizados (os dados permaneceram intactos). É fato que, para qualquer tarefa, um determinado intervalo de parâmetros funciona melhor que outros. Com isso em mente, você está embarcando em um caminho de aprendizado bem-sucedido.
Obrigada