Olá pessoal! O desenvolvimento do hexapod está avançando e, finalmente, a parte matemática básica foi testada e pronta para documentação. Para que o projeto sobreviva até o fim e não acumule poeira na prateleira, você precisa ver suas mudanças positivas, mesmo que sejam insignificantes. Neste artigo, falarei sobre um algoritmo para resolver o problema de cinemática inversa e o demonstrarei em ação. Espero que seja interessante.
Etapas do desenvolvimento:Parte 1 - DesignParte 2 - montagemParte 3 - CinemáticaParte 4 - trajetórias e sequências matemáticasParte 5 - EletrônicaParte 6 - transição para impressão 3DParte 7 - nova caixa, software aplicativo e protocolos de comunicaçãoSistemas de coordenadas
Para começar, é necessário determinar os sistemas de coordenadas do robô - existem até três:
De fato, eles não são diferentes um do outro, mas estão localizados em locais diferentes do caso e podem ser girados um em relação ao outro em algum ângulo. Quando vista de cima, a localização dos eixos será a seguinte (o parâmetro coxa_zero_rotate será descrito um pouco mais tarde):
Como você provavelmente já percebeu, os sistemas de coordenadas nos lados esquerdo e direito estão localizados simetricamente em relação ao centro do corpo. Pareceu-me que seria mais fácil.
As coordenadas de cada ponto são definidas em relação ao membro para o qual este ponto se destina. Essa abordagem permite mover o membro sem dor em qualquer lugar, sem interferir na configuração.
E assim eles estão localizados em relação ao membro:
As coordenadas do ponto de destino são relativas ao SISTEMA DE COORDENADAS PRINCIPAIS. Inicialmente, eu queria definir as coordenadas relativas ao centro do caso, mas isso não era muito conveniente e exigia o armazenamento de vários parâmetros adicionais.
A seguir, a notação X *, X **, etc. será substituído por X ′, X ′ ′.
Resolvendo o problema de cinemática inversa
Vamos começar com o momento mais difícil e interessante para mim - a cinemática. Eu mesmo inventei o algoritmo, às vezes olhando as propriedades de um triângulo e funções trigonométricas. Com a mecânica, é difícil para mim, e com a trigonometria é ainda pior, então talvez em algum lugar eu não pudesse levar algo em consideração, mas esse algoritmo funciona (vídeo no final).
1. Declaração do problema
Suponha que precisamos do membro frontal direito para alcançar o ponto A com coordenadas (150; -20; 100). Sabe-se também que o membro é girado em relação ao corpo em 45 graus (parâmetro coxa_zero_rotate):
O membro em si possui os seguintes parâmetros:
Eu acho que você não precisa descrever o que esses parâmetros significam, os nomes falam por si. Você pode adicionar apenas que todos esses parâmetros sejam determinados pela configuração do gabinete, sejam permanentes e armazenados na memória FLASH, com a capacidade de editar de fora (para flexibilidade).
É por isso que você precisa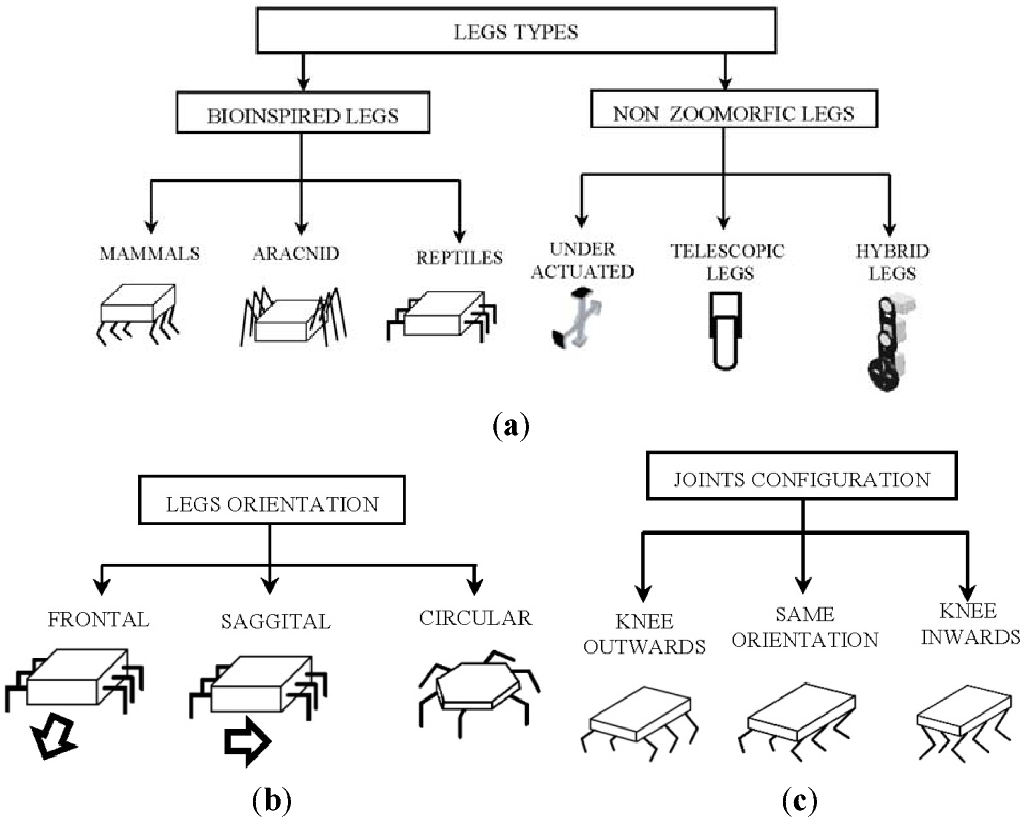
A imagem mostra várias variações do casco e a localização das pernas do hexápode. Agora, ele corresponde à configuração do ARACNID. Suponha que me ocorreu mudar o caso para REPTILES e, para isso, será bastante simples alterar os valores dos parâmetros sem medir no próprio programa, mesmo os pontos de destino não precisarão ser alterados (a menos que, é claro, se aproxime corretamente).
Todos os parâmetros acima são suficientes para resolver o problema.
2. A solução para o problema
2.1 Encontrar o ângulo de rotação do COXAEsta etapa é a mais simples. Primeiro, você precisa recalcular as coordenadas do ponto A em relação ao SISTEMA DE COORDENADAS DE MEMBROS. Obviamente, você precisa girar o ângulo coxa_zero_rotate, pode fazer isso usando as seguintes fórmulas:
$$ display $$ x ′ = x ⋅ cos (α) + z ⋅ sin (α) = 150 ⋅ cos (45) + 100 ⋅ sin (45) = 176,78 $$ display $$
y′=y=−20
$$ display $$ z ′ = -x ⋅ sin (α) + z ⋅ cos (α) = -150 ⋅ sin (45) + 100 ⋅ cos (45) = -35,36 $$ display $$
Assim, obtivemos as coordenadas do ponto de destino A (176,78; -20; -35,36) em relação ao SISTEMA DE COORDENADAS DE MEMBROS.
Agora você pode encontrar o ângulo COXA usando a função atan2:
COXA=atan2(z′,x′)=atan2(−35,36,176,78)=−11,30
E assim, temos o ângulo pelo qual você precisa girar o servo COXA para que o ponto A esteja no plano X′Y '. Vamos agora verificar nossos cálculos no KOMPAS 3D:
Tudo bem.
2.2 Encontrando o ângulo de rotação do FEMUR e da TIBIAPara encontrar esses ângulos, é necessário ir para o plano X′Y '. Para ir para o plano, você precisa girar o ponto pelo ângulo COXA, que já calculamos anteriormente.
$$ display $$ x ′ = x ′ ⋅ cos (α) + y ′ ⋅ sen (α) = 176,78 ⋅ cos (-11) + -20 ⋅ sin (-11) = 180,28 $$ display $$
y′=y=−20
A coordenada
y ' não muda, à medida que giramos ao longo do eixo Y'.
Em seguida, é necessário remover o comprimento da COXA do cálculo, ou seja, passamos para o plano X′′Y ′, para isso realizamos um deslocamento da coordenada
x ′ do ponto pelo comprimento COXA:

y′′=y′
Depois de todas essas manipulações, a solução adicional do problema é reduzida para encontrar os ângulos
aeb do triângulo:
Antes de encontrar os ângulos, você precisa encontrar o terceiro lado C deste triângulo. Essa distância nada mais é que o comprimento do vetor e é calculada pela fórmula:
$$ display $$ C = \ sqrt {x ′ ′ ^ 2 + y ′ ′ ^ 2} = \ sqrt {140,28 ^ 2 + (-20) ^ 2} = 141,70 $$ display $$
Agora você precisa verificar se o membro pode chegar a esse ponto. Se C for maior que a soma dos comprimentos de FEMUR e TIBIA, o ponto não será alcançável. No nosso caso, 141,70 <141 + 85 - o ponto é alcançável.
Agora conhecemos todos os lados do triângulo e podemos encontrar os ângulos
a e
b que precisamos usando o teorema do cosseno:
a=acos(A2+C2−B2 over2AC)=72,05°
b=acos(B2+A2−C2 over2BA)=72,95°
Os ângulos obtidos não são aplicáveis para alimentá-los com servos, uma vez que a posição inicial e o ângulo de inclinação da linha reta C em relação ao eixo X não são levados em consideração aqui. Se conhecermos os ângulos iniciais FEMUR e TIBIA (135 ° e 45 °), então o ângulo de inclinação C em relação ao eixo X não é conhecido. Você pode encontrá-lo usando a função atan2 (y ′ ′, x ′ ′):
$$ display $$ φ = atan2 (y ′ ′, x ′ ′) = atan2 (-20, 140,28) = -8,11 ° $$ display $$
Finalmente, você pode calcular o ângulo de rotação dos servos FEMUR e TIBIA:
FEMUR=femurZeroRotate−a−φ=135−72,05+8,11=71,06°
FEMUR=b−tibiaZeroRotate=45−72,95=27,95°
Vamos verificar nossos cálculos:
Parece a verdade.
Sumário
Os ângulos calculados COXA, FEMUR e TIBIA são adequados para alimentar seus servos. Você pode notar que o ângulo COXA é negativo e, portanto, surge a pergunta: “Como girar o inversor em -11,3 graus?”. O truque é que eu uso a posição neutra do servo COXA como um zero lógico, isso permite que o inversor gire ângulos positivos e negativos. Isso é obviamente óbvio, mas acho que não seria impróprio mencionar isso. Vou falar mais sobre isso nos artigos a seguir, quando falar sobre a implementação de todos os itens acima.
Código fonte
Palavras suficientes, deixe-me ver o código#define RAD_TO_DEG(rad) ((rad) * 180.0 / M_PI) #define DEG_TO_RAD(deg) ((deg) * M_PI / 180.0) typedef enum { LINK_COXA, LINK_FEMUR, LINK_TIBIA } link_id_t; typedef struct {
Algoritmo em ação
Então, por acaso, apareceu uma sequência que lembrava uma dança
PS
Eu ficaria feliz se alguém puder simplificar esse algoritmo. Eu fiz isso para que eu pudesse entender depois de, digamos, meio ano.