Em nossa era, as máquinas alcançaram 99% de precisão na compreensão e definição de recursos e objetos nas imagens. Encontramos isso todos os dias, por exemplo: reconhecimento de rosto na câmera do smartphone, capacidade de procurar fotos no google, digitalizar texto de um código de barras ou livros a uma boa velocidade etc. Essa eficiência da máquina é possível graças a um tipo especial de rede neural chamada convolucional neural a rede. Se você é um entusiasta do aprendizado profundo, provavelmente já ouviu falar sobre isso e pode desenvolver vários classificadores de imagem. As estruturas modernas de aprendizado profundo, como Tensorflow e PyTorch, simplificam o aprendizado de máquina de imagem. No entanto, a questão ainda permanece: como os dados passam pelas camadas da rede neural e como o computador aprende com elas? Para obter uma visão clara do zero, mergulhamos em uma convolução, visualizando a imagem de cada camada.
Redes neurais convolucionais
Antes de começar a estudar redes neurais convolucionais (SNA), você precisa aprender a trabalhar com redes neurais. As redes neurais imitam o cérebro humano para resolver problemas complexos e procurar padrões nos dados. Nos últimos anos, eles substituíram muitos algoritmos de aprendizado de máquina e visão computacional. O modelo básico de uma rede neural consiste em neurônios organizados em camadas. Cada rede neural possui uma camada de entrada e saída e várias camadas ocultas, dependendo da complexidade do problema. Ao transmitir dados através de camadas, os neurônios são treinados e reconhecem sinais. Essa representação de uma rede neural é chamada de modelo. Após o treinamento do modelo, solicitamos à rede que faça previsões com base nos dados do teste.
O SNS é um tipo especial de rede neural que funciona bem com imagens. Ian Lekun os propôs em 1998, onde reconheceram o número presente na imagem de entrada. O SNA também é usado para reconhecimento de fala, segmentação de imagens e processamento de texto. Antes da criação de redes neurais convolucionais, perceptrons multicamadas eram usados na construção de classificadores de imagem. A classificação de imagem refere-se à tarefa de extrair classes de uma imagem raster multicanal (colorida, preto e branco). Os perceptrons de múltiplas camadas levam muito tempo para procurar informações nas imagens, pois cada entrada deve estar associada a cada neurônio na próxima camada. O SNA os contornou usando um conceito chamado conectividade local. Isso significa que conectaremos cada neurônio apenas à região de entrada local. Isso minimiza o número de parâmetros, permitindo que várias partes da rede se especializem em atributos de alto nível, como textura ou padrão de repetição. Confuso? Vamos comparar como as imagens são transmitidas através de perceptrons de múltiplas camadas (MPs) e redes neurais convolucionais.
Comparação de MP e SNA
O número total de entradas na camada de entrada para o perceptron de múltiplas camadas será 784, pois a imagem de entrada é 28x28 = 784 (o conjunto de dados MNIST é considerado). A rede deve ser capaz de prever o número na imagem de entrada, o que significa que a saída pode pertencer a qualquer uma das seguintes classes no intervalo de 0 a 9. Na camada de saída, retornamos estimativas de classe, digamos, se essa entrada for a imagem com o número "3", então, na camada de saída, o neurônio correspondente "3" tem um valor mais alto em comparação com outros neurônios. Novamente, surge a pergunta: "Quantas camadas ocultas precisamos e quantos neurônios devem existir em cada uma?" Por exemplo, use o seguinte código MP:
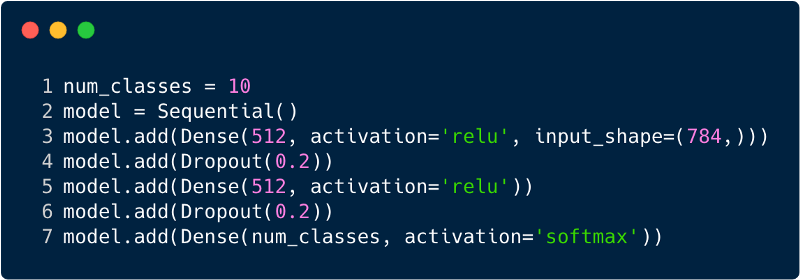
O código acima é implementado usando uma estrutura chamada Keras. A primeira camada oculta possui 512 neurônios conectados à camada de entrada de 784 neurônios. A próxima camada oculta: a camada de exclusão, que resolve o problema de reciclagem. 0.2 significa que há uma chance de 20% de não levar em consideração os neurônios da camada oculta anterior. Novamente, adicionamos uma segunda camada oculta com o mesmo número de neurônios da primeira camada oculta (512) e depois outra camada exclusiva. Finalmente, finalizando esse conjunto de camadas com uma camada de saída composta por 10 classes. A classe que mais importa será o número previsto pelo modelo. É assim que uma rede multicamada cuida da identificação de todas as camadas. Uma das desvantagens do perceptron de vários níveis é que ele está totalmente conectado, o que demanda muito tempo e espaço.
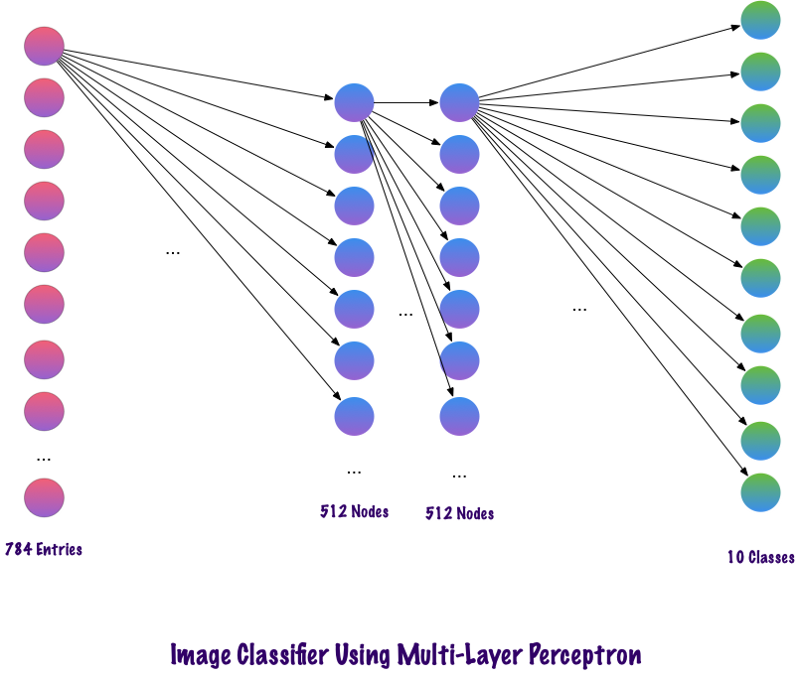
Convolts não usam camadas totalmente unidas. Eles usam camadas esparsas, que recebem matrizes como entrada, o que oferece uma vantagem sobre o MP. No MP, cada nó é responsável por entender toda a imagem. No SNA, dividimos a imagem em áreas (pequenas áreas locais de pixels). A camada de saída combina os dados recebidos de cada nó oculto para encontrar padrões. Abaixo está uma imagem de como as camadas estão conectadas.
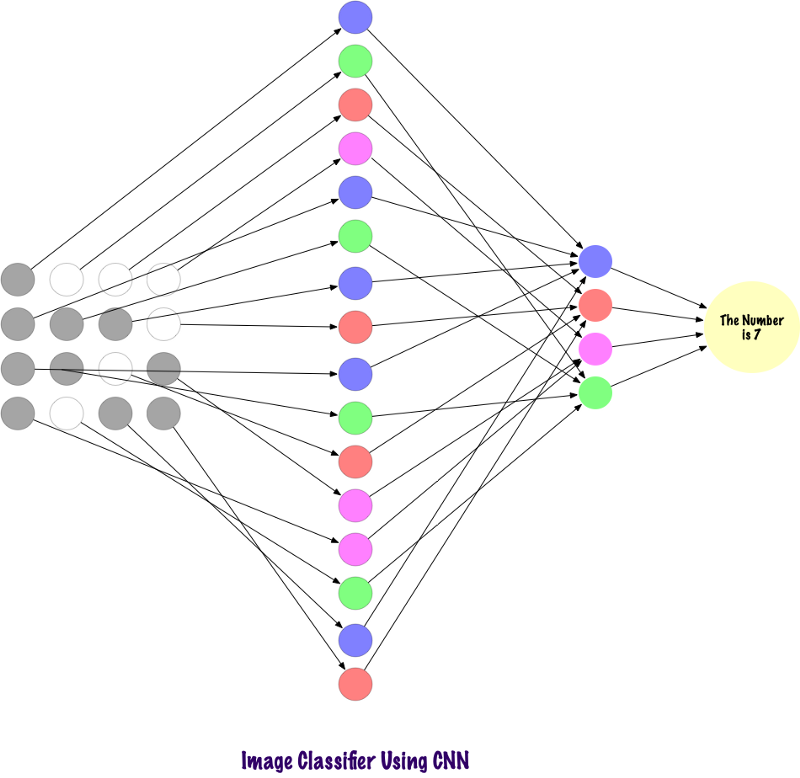
Agora vamos ver como o SNA encontra informações nas fotografias. Antes disso, precisamos entender como os sinais são extraídos. No SNA, usamos camadas diferentes, cada camada preserva os sinais da imagem, por exemplo, leva em conta a imagem do cão, quando a rede precisa classificá-lo, deve identificar todos os sinais, como olhos, ouvidos, língua, pernas, etc. Esses sinais são quebrados e reconhecidos nos níveis da rede local usando filtros e núcleos.
Como os computadores olham para uma imagem?
Uma pessoa que olha uma imagem e entende seu significado parece bastante razoável. Digamos que você ande e observe as muitas paisagens ao seu redor. Como entendemos a natureza nesse caso? Tiramos fotos do ambiente usando nosso principal órgão sensorial - o olho, e depois o enviamos para a retina. Tudo parece bem interessante, certo? Agora vamos imaginar que um computador faça o mesmo. Nos computadores, as imagens são interpretadas usando um conjunto de valores de pixel que variam de 0 a 255. O computador examina esses valores de pixel e os entende. À primeira vista, ele não conhece objetos e cores. Ele simplesmente reconhece os valores de pixel e a imagem é equivalente a um conjunto de valores de pixel para o computador. Mais tarde, analisando os valores de pixel, ele aprende gradualmente se a imagem é cinza ou colorida. As imagens em escala de cinza têm apenas um canal, pois cada pixel representa a intensidade de uma cor. 0 significa preto e 255 significa branco, as outras variantes de preto e branco, ou seja, cinza, estão entre elas.
As imagens coloridas possuem três canais, vermelho, verde e azul. Eles representam a intensidade de três cores (matriz tridimensional) e, quando os valores mudam simultaneamente, isso fornece um grande conjunto de cores, realmente uma paleta de cores! Depois disso, o computador reconhece as curvas e contornos dos objetos na imagem. Tudo isso pode ser estudado na rede neural convolucional. Para isso, usaremos o PyTorch para carregar um conjunto de dados e aplicar filtros às imagens. A seguir, é um trecho de código.
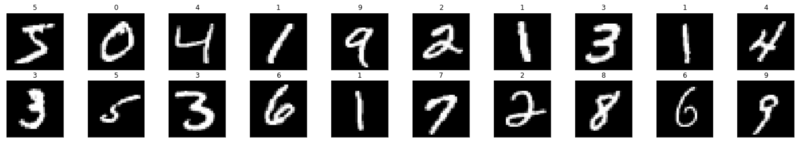
Agora vamos ver como uma única imagem é inserida em uma rede neural.
img = np.squeeze(images[7]) fig = plt.figure(figsize = (12,12)) ax = fig.add_subplot(111) ax.imshow(img, cmap='gray') width, height = img.shape thresh = img.max()/2.5 for x in range(width): for y in range(height): val = round(img[x][y],2) if img[x][y] !=0 else 0 ax.annotate(str(val), xy=(y,x), color='white' if img[x][y]<thresh else 'black')
É assim que o número "3" é dividido em pixels. No conjunto de dígitos manuscritos, “3” é selecionado aleatoriamente, no qual os valores de pixel são exibidos. Aqui ToTensor () normaliza os valores reais de pixel (0–255) e os limita a um intervalo de 0 a 1. Por que isso? Porque facilita os cálculos nas seções subseqüentes, seja para interpretar imagens ou para encontrar padrões comuns que existem nelas.
Crie seu próprio filtro
Os filtros, como o nome indica, filtram as informações. No caso de redes neurais convolucionais, ao trabalhar com imagens, as informações sobre os pixels são filtradas. Por que devemos filtrar? Lembre-se de que um computador deve passar por um processo de aprendizado para entender imagens, muito parecido com o que a criança faz. Nesse caso, no entanto, não precisaremos de muitos anos! Em suma, ele aprende do zero e depois avança para o todo.
Portanto, a rede deve conhecer inicialmente todas as partes grosseiras da imagem, como bordas, contornos e outros elementos de baixo nível. Uma vez descobertos, o caminho para sintomas complexos é pavimentado. Para chegar a eles, precisamos primeiro extrair os atributos de baixo nível, depois o meio e, em seguida, os de nível superior. Os filtros são uma maneira de extrair as informações de que o usuário precisa, e não apenas a transferência cega de dados, por causa da qual o computador não entende a estrutura das imagens. No começo, funções de baixo nível podem ser extraídas com base em um filtro específico. O filtro aqui também é um conjunto de valores de pixel, semelhante a uma imagem. Pode ser entendido como os pesos que conectam as camadas na rede neural convolucional. Esses pesos ou filtros são multiplicados pelos valores de entrada para produzir imagens intermediárias que representam o entendimento da imagem por computador. Em seguida, eles são multiplicados por mais alguns filtros para expandir a exibição. Em seguida, ele detecta os órgãos visíveis de uma pessoa (desde que uma pessoa esteja presente na imagem). Mais tarde, com a inclusão de vários outros filtros e várias camadas, o computador exclama: “Ah, sim! Este é um homem. "
Se falamos de filtros, temos muitas opções. Você pode desfocar a imagem e aplicar um filtro de desfoque; se precisar adicionar nitidez, um filtro de nitidez será resgatado etc.
Vejamos alguns trechos de código para entender a funcionalidade dos filtros.
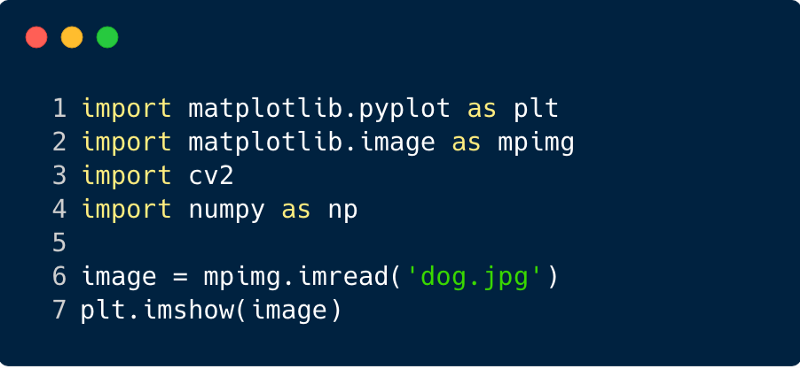
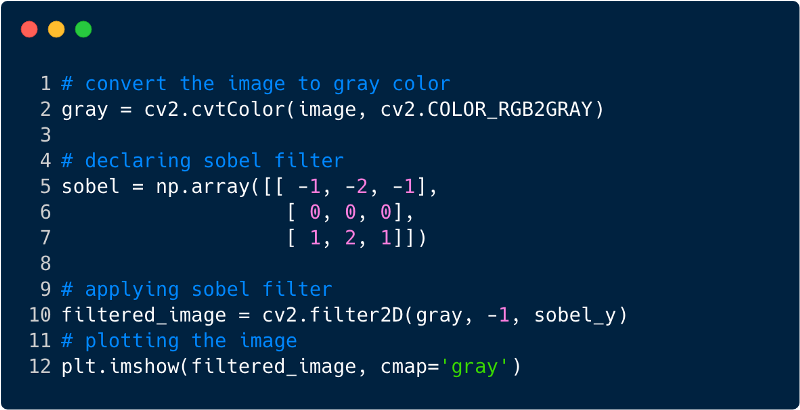
É assim que a imagem é aplicada após a aplicação do filtro. Nesse caso, usamos o filtro Sobel.
Redes neurais convolucionais
Até agora, vimos como os filtros são usados para extrair recursos das imagens. Agora, para completar toda a rede neural convolucional, precisamos conhecer todas as camadas que usamos para projetá-la. As camadas usadas no SNA,
- Camada convolucional
- Camada de pool
- Camada totalmente colada
Com todas as três camadas, o classificador de imagem convolucional fica assim:
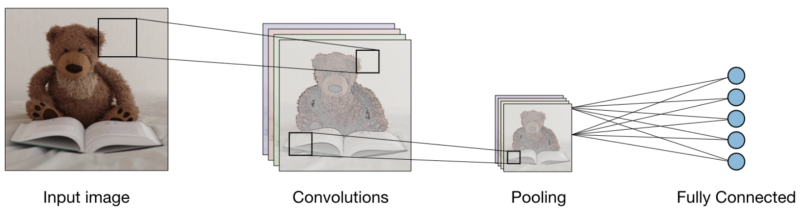
Agora vamos ver o que cada camada faz.
A camada convolucional (CONV) usa filtros que executam operações de convolução digitalizando a imagem de entrada. Seus hiperparâmetros incluem um tamanho de filtro, que pode ser 2x2, 3x3, 4x4, 5x5 (mas não limitado a isso) e a etapa S. O resultado O é chamado de mapa de recurso ou mapa de ativação no qual todos os recursos são calculados usando camadas e filtros de entrada. Abaixo está uma imagem da geração de mapas de recursos ao aplicar a convolução,
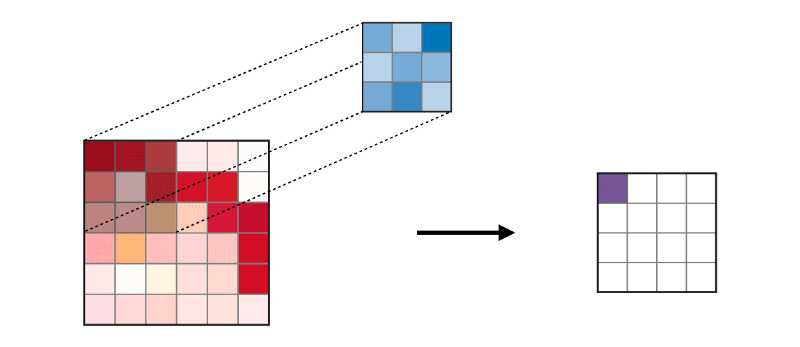A camada de mesclagem (POOL) é usada para compactar os recursos normalmente usados após a camada de convolução. Existem dois tipos de operações de união - essa é a união máxima e média, na qual os valores máximo e médio das características são obtidos, respectivamente. A seguir está a operação de operações de mesclagem,
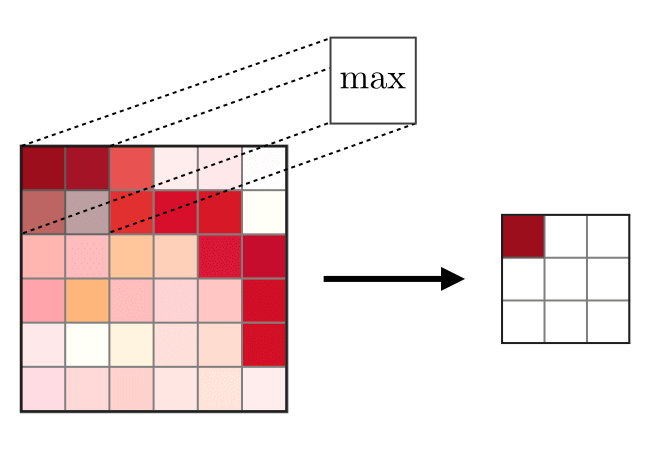
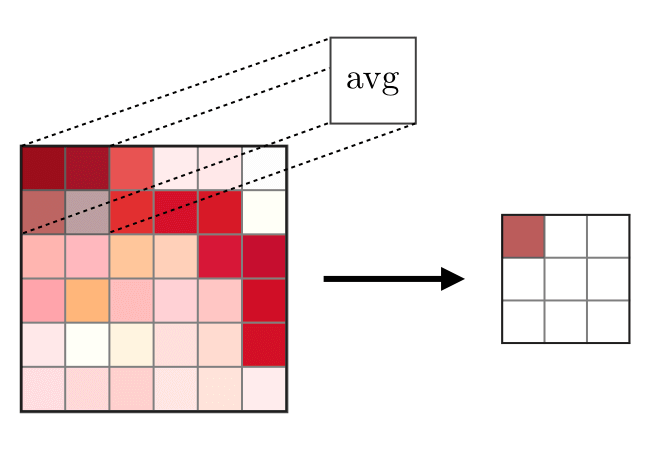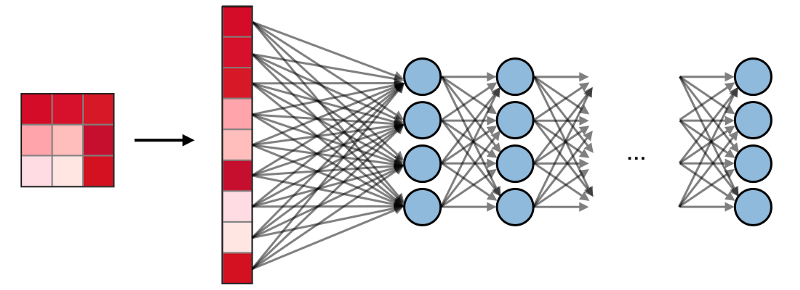
As camadas totalmente conectadas (FCs) operam com uma entrada plana, onde cada entrada é conectada a todos os neurônios. Eles geralmente são usados no final da rede para conectar camadas ocultas à camada de saída, o que ajuda a otimizar as pontuações das turmas.
Visualização SNA no PyTorch
Agora que temos a ideologia completa da criação do SNA, vamos implementá-lo usando a estrutura PyTorch do Facebook.
Etapa 1 : faça o download da imagem de entrada a ser enviada pela rede. (Aqui fazemos isso com Numpy e OpenCV)
import cv2 import matplotlib.pyplot as plt %matplotlib inline img_path = 'dog.jpg' bgr_img = cv2.imread(img_path) gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
Etapa 2 : renderizar filtros
Vamos visualizar os filtros para entender melhor quais usaremos,
import numpy as np filter_vals = np.array([ [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1] ]) print('Filter shape: ', filter_vals.shape)
Etapa 3 : Determinar o SNA
Esse SNA possui uma camada convolucional e uma camada de pool com uma função máxima, e os pesos são inicializados usando os filtros mostrados acima,
import torch import torch.nn as nn import torch.nn.functional as F class Net(nn.Module): def __init__(self, weight): super(Net, self).__init__()
Net( (conv): Conv2d(1, 4, kernel_size=(4, 4), stride=(1, 1), bias=False) (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) )
Etapa 4 : renderizar filtros
Uma rápida olhada nos filtros usados,
def viz_layer(layer, n_filters= 4): fig = plt.figure(figsize=(20, 20)) for i in range(n_filters): ax = fig.add_subplot(1, n_filters, i+1) ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray') ax.set_title('Output %s' % str(i+1)) fig = plt.figure(figsize=(12, 6)) fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05) for i in range(4): ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[]) ax.imshow(filters[i], cmap='gray') ax.set_title('Filter %s' % str(i+1)) gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
Filtros:
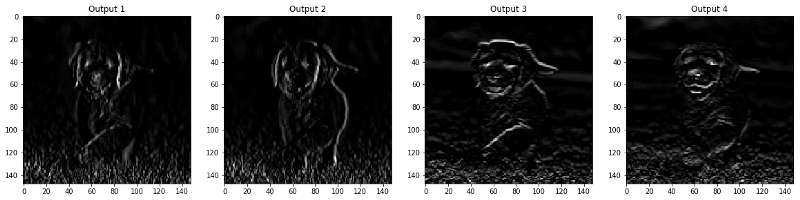
Etapa 5 : Resultados filtrados por camada
As imagens que aparecem na camada CONV e POOL são mostradas abaixo.
viz_layer(activated_layer) viz_layer(pooled_layer)
Camadas convolucionais
Camadas de pool
Fonte