A declaração do problema

Eu estava navegando na Internet outro dia e uma coisa bastante curiosa me chamou a atenção: o motor Mendocino . É um rotor de rolamento de baixa fricção: o original tinha um cilindro de vidro pendurado em duas agulhas, mas os modernos usam suspensão magnética. É um motor sem escovas: o rotor possui baterias solares, que geram corrente para as bobinas enroladas ao redor do rotor. O rotor gira em um campo magnético fixo, as baterias solares são expostas à fonte de luz uma após a outra. É uma solução bastante elegante que é muito possível recriar em casa.

Aqui está o vídeo que explica como funciona (em russo):


Mas este vídeo teve outra curiosidade ainda mais forte que o próprio motor. Na descrição do vídeo, Dmitry Korzhevsky escreve: “Você não pode substituir o suporte lateral por um ímã! Não me pergunte mais sobre isso!

Isenção de responsabilidade: eu não sou especialista em física e pode estar muito errado em algumas coisas; portanto, as correções são bem-vindas.



Vamos discutir mais uma vez como o sistema de suspensão magnética do rotor funciona. Se pegarmos dois ímãs, a isolina em potencial se parece com isso, dependendo da distância entre os ímãs:



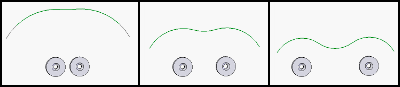
Então, colocamos dois ímãs fixos em um estator. O ímã colocado no eixo do rotor não vai querer se mover para o lado, pois a isolina em potencial tem um certo ponto mínimo local. Em vez disso, gostaria de saltar ao longo do eixo do rotor. Fabricamos dois desses sistemas e, no final, o eixo do rotor é estável radialmente, mas é instável lateralmente. Corrigimos isso inclinando o rotor contra uma parede de vidro e pronto - temos um rolamento de baixa fricção.

Mas a parede de vidro é um pouco ... não esteticamente agradável, não é? É lógico que queremos suspender completamente o rotor no ar, sem muletas mecânicas como essa. E, evidentemente, Dmitry também foi bombardeado com a mesma pergunta, e é por isso que ele teve que observar bem na descrição que isso é impossível. E aposto que Dmitry não é o único que se cansou disso.

Vamos ver isso, cito:

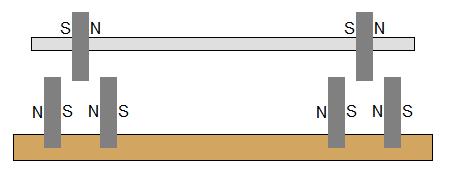
O que aconteceria se os ímãs de base fossem espaçados e orientados como neste desenho? Isso daria estabilidade no plano axial e eliminaria o requisito de espelho?

Ou aqui , cito:

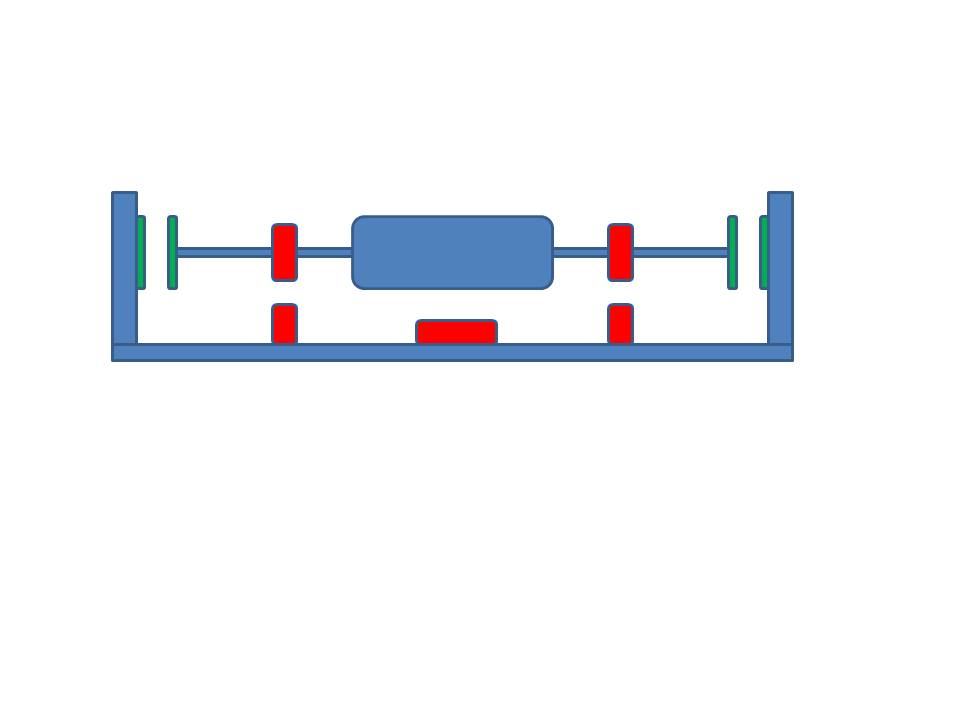
Em um motor Mendocino, por que um lado flutua livre enquanto o outro tem uma ponta na parede? Eu sei que a pergunta pode parecer trivial, mas eu desenvolvi a idéia de por que não usar os mesmos ímãs usados ​​para levitar como uma força contrária nos dois lados do eixo? Anexei um jpg muito áspero do que quero dizer. é o que eu estou me referindo aos ímãs verdes no final dos eixos. existe alguma teoria ou lei que impeça isso?

Podemos ver que muitas pessoas ao redor do mundo querem se livrar dessa parte mecânica inadequada. Eu não estava prestando muita atenção nos meus tempos de escola, por isso não me era óbvio por que um sistema de suspensão magnética completamente estável era inviável. Um dia, no almoço, fiz essa pergunta ao meu supervisor, um cientista mundialmente famoso (em matemática aplicada, não em física): "Por que isso é impossível?". E você sabe o que, ele também não sabia!

Os fóruns postados acima também não forneceram uma resposta adequada para essa pergunta. Na melhor das hipóteses, alguém se referiu a algo chamado teorema de Earnshaw , que não se presta à compreensão à primeira vista. Ele afirma que: uma coleção de cargas pontuais não pode ser mantida em uma configuração de equilíbrio estacionário estável apenas pela interação eletrostática das cargas. Você entendeu? Eu certamente não. Digamos que eu possa aceitar o fato de estarmos falando de cobranças e não de ímãs. Então o que?

Primeira ilustração

Quando não consigo enrolar a cabeça em torno de algo, costumo desenhá-lo. Vamos ilustrar isso em 2D, para simplificar. Imagine quatro cargas fixas, colocadas em um padrão quadrado, mais uma carga gratuita no centro. Assim:



A carga livre não está em equilíbrio, então? Não importa para onde se mova, ele se aproxima de uma das cargas fixas, o que aumenta a força de empurrão! Vamos tentar desenhar um mapa da energia potencial de uma carga gratuita. Eu perdi muitas aulas de física na escola, então meu repositório de conhecimento é a Wikipedia. Portanto, se você tiver apenas uma carga fixa, isso cria potencial eletrostático no campo ao seu redor:

A equação do potencial eletrostático (ou potencial de Coulomb) de uma carga pontual no vácuo:

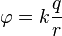
Em todas as minhas experiências de pensamento, todos os coeficientes são 0 ou 1. Portanto, a carga q é 1 e o k desconhecido também é 1. Isso significa que uma carga fixa cria energia potencial medida como 1 / r, onde r é a distância da cobrar.

No nosso caso, a energia potencial da carga livre dentro do campo da carga fixa também é igual a 1 / r. (para ser justo, a energia é igual a k * q1 * q2 / r, mas escolhemos os coeficientes para facilitar os cálculos). Para várias cobranças, simplesmente adicionamos todos os potenciais.

Vamos desenhar um mapa da energia potencial de nossa tarifa gratuita. Eu uso sálvia para isso:

var('x,y') def unit_potential(a,b,x,y): return 1/(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Aqui está o nosso mapa. Pontos brancos (perfurados) é onde a energia potencial se torna infinita:



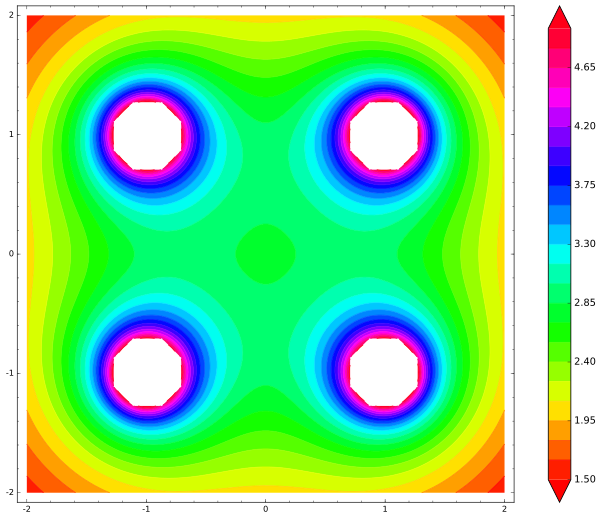
Vemos claramente o mínimo local de energia no centro. Onde quer que a carga central queira se mover, a energia aumentará, então pequenos distúrbios a forçarão de volta ao centro - o ponto de equilíbrio estável. Earnshaw estava errado, então? Não, ele não estava, apenas desenhei a ilustração incorretamente. E isso é um erro comum entre as pessoas que fazem essa pergunta. Pare por alguns minutos agora e adivinhe: o que eu perdi?

De fato, neste caso, o erro foi que, em um espaço bidimensional, a carga fixa cria energia potencial medida como -ln r, onde r é a distância da carga e não 1 / r. Apenas tome minha palavra por enquanto e deixe-me corrigir a equação sem explicar muito. O código correto é assim:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

E este é o mapa que produz:



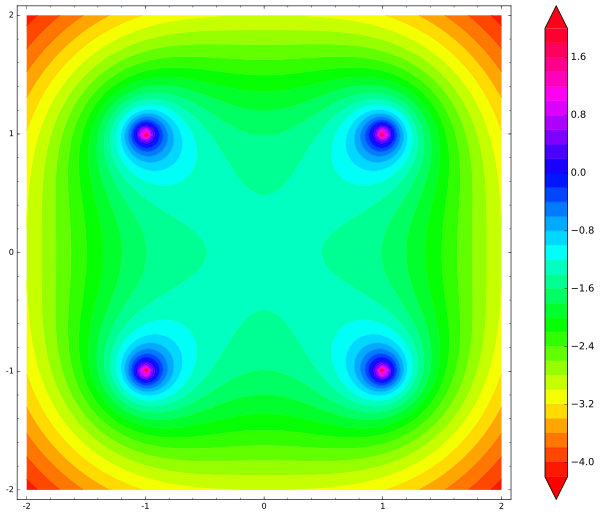
Observe que não há um mínimo local em nenhum lugar. O centro é o ponto de sela, ou o ponto de equilíbrio instável . Assim que a carga gratuita se afastar até um mícron do centro, ela inevitavelmente sairá do sistema, acelerando ao longo do caminho,

Espere um segundo, o que você acabou de fazer na equação?

Inicialmente, quando percebi que meus cálculos eram totalmente contrários ao teorema de Earnshaw, percebi que cometi um erro em algum lugar. É mais fácil rastrear meus passos desde o início. Respirei fundo e fui ler sobre as equações de Maxwell . Novamente, eu não era muito bom na escola: não nas notas (estas eram excelentes), mas na quantidade de conhecimento que tirei dela. Por exemplo, eu esqueci imediatamente as equações de Maxwell, já que na universidade e além não precisava trabalhar com elas.

Acontece que eles são bastante simples, especialmente se estamos falando apenas de leis eletrostáticas! Existem quatro equações de Maxwell, uma para cada uma dessas leis:

• A lei de Gauss, precisamos dela mais tarde. Em suma, é uma lei de conservação: a energia não pode ser criada do nada, nem pode ser destruída.
• A lei de Gauss para campos magnéticos, que é essencialmente a mesma coisa. E ainda não entramos em campos magnéticos, já que estamos falando apenas de partículas carregadas. Ignore essa lei.
• A lei de Faraday: ímãs em movimento criam um campo elétrico. Isso é interessante, veremos mais tarde.
• A lei Amper: mover um campo elétrico cria um campo magnético. Inútil para nossos propósitos.

Portanto, essas quatro leis ligam dois vetores E e B, campos elétricos e magnéticos. Esses vetores são funções com quatro argumentos (x, y, z, t) e cada quatro argumentos é justaposto a um vetor tridimensional. Nós não estamos tão interessados ​​em campos magnéticos, então vamos dar uma olhada nos campos elétricos ou E (x, y, z, t). Não esqueça que estamos no reino eletrostático, então E é constante ao longo do tempo. Você pode imaginar esse vetor como um rio, onde em cada ponto dizemos onde e com que velocidade a água vai.

A lei de Faraday declara que um campo E constante no tempo (estamos falando de eletrostática lá) não tem curvatura .

Como o potencial eletrostático está conectado aos campos elétricos? Simples: se o campo E é sem ondulação (como é o caso), podemos criar u de uma maneira que (voltando ao exemplo do rio), coberta por uma camada de 1 metro de água (em todas as alturas! ) e “liberando: a velocidade e a direção do fluxo da água criariam o campo E. Ou, em termos matemáticos, é possível encontrar uma função escalar u, cujo gradiente é igual ao campo E.

A lei de Gauss declara: faça um pequeno bairro. Se não cobrarmos deliberadamente, a quantidade de “água” que flui para a vizinhança é igual à quantidade que sai. Se queremos parecer inteligentes, a divergência do campo E é zero.

Lembre-se: o campo E é um derivado da função escalar u. Se a sua divergência é zero, significa que o laplaciano de u é zero. Laplaciano é uma palavra inteligente para a "curvatura" da função. Se estamos falando de funções de uma variável, o Laplaciano é simplesmente a segunda derivada. Nas funções de duas variáveis, o laplaciano é a soma de duas derivadas. Se for igual a zero, a curvatura em uma direção deve ser cancelada pela curvatura na outra direção. Significado, batatas fritas podem existir:



Mas a função zero-laplaciano não possui mínimos locais (ou máximos), o que significa que batatas fritas são permitidas, mas as montanhas não são:



Imagine mergulhar um círculo (curvo) de arame na água e sabão. O filme de sabão forma então uma superfície com laplaciano zero:



Será a chamada "superfície mínima". O filme de sabão tenta ser o menor possível, por isso é lógico que, se tivesse um determinado máximo local, teríamos um filme menor suavizando-o, para que não haja nenhum. Portanto, o potencial eletrostático é uma espécie de superfície mínima que não possui máximos locais (desde que não tenhamos carregado deliberadamente).

A função 1 / r tem um laço laplaciano zero em três dimensões, mas não em duas! Se quisermos desenhar exemplos bidimensionais, precisaríamos resolver um problema de Dirichlet - para 2D, é -ln r.

O uso da fórmula dos quadrados inversos no espaço 1 ou 2 dimensional corresponde a restringir o movimento de cargas ao longo dos demais eixos de alguma outra maneira. Nesse caso, é óbvio que é possível fazer uma configuração estável - basta pegar um tubo de papelão, colocá-lo na vertical e abaixar seu ímã. Então é possível colocar lá mais um ímã que estará em equilíbrio - horizontalmente, ele é restringido pelo tubo (ou seja, está no espaço unidimensional), e em uma força vertical de gravidade e repulsão de um ímã são contrabalançados. O teorema de Earnshaw precisa ser aplicado com a lei dos quadrados inversos - mas em 3d, ou no espaço de qualquer dimensão, mas com o potencial correspondente. "Correspondente" significa aquele obtido a partir das equações de Maxwell.

Teorema de Earnshaw e suas conseqüências

Então, voltando ao nosso exemplo com uma partícula carregada gratuitamente. O potencial de um campo eletrostático não possui mínimos locais e, como resultado, a energia potencial da partícula não possui mínimos locais. Portanto, uma partícula não pode alcançar um equilíbrio estável em um campo estático. Parabéns, acabamos de provar o teorema de Earnshaw. Mas e quanto a sistemas mais complicados? Como aplicar o teorema aí?

Aqui está outro exemplo que, de acordo com meu chefe, deveria ter desmentido o teorema de Earnshaw. Vamos corrigir duas cargas e criar um corpo em movimento que consiste em um manípulo não elástico e sem peso, com cargas nas duas extremidades:



Intuitivamente, se movermos o manípulo levemente para a esquerda ou para a direita, uma das extremidades se aproximará das cargas fixas, o que o empurrará e retornará o manípulo de volta à posição original. Então, qual é o problema? Vamos desenhar um mapa do potencial eletrostático de duas cargas fixas:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

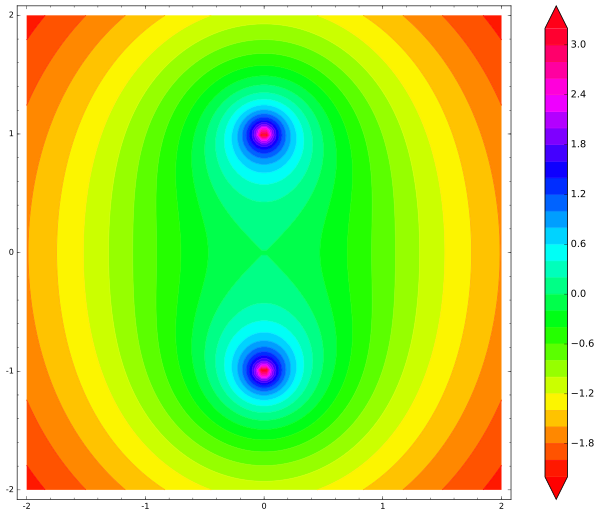
Como ilustramos a energia potencial do nosso bastão? O stick possui três graus de liberdade (dois para movimento e um para rotação); portanto, o gráfico seria quadridimensional. Vamos ignorar a rotação por enquanto e apenas deixar o manípulo se mover de um lado para o outro. Fixamos um ponto em um bastão (por exemplo, seu centro) e desenhamos o mapa da energia potencial do bastão para seu centro. Nesse caso, a energia potencial total do bastão é a soma das energias potenciais de suas cargas nas duas extremidades:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y) contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

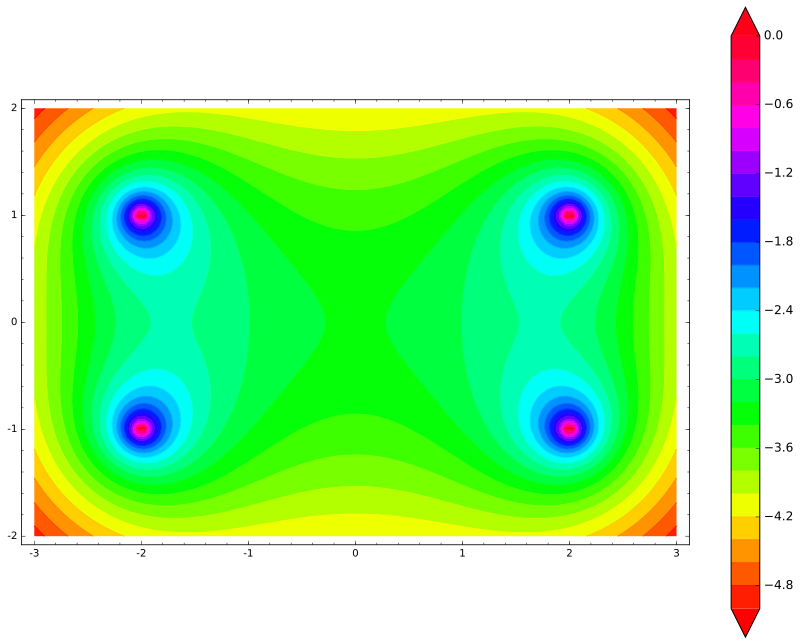
Portanto, a energia do bastão tem quatro picos (cada extremidade pode atingir cada uma das duas cargas). Como esperado, o stick não se moveria horizontalmente - em vez disso, se moveria verticalmente!

É lógico, pois como conseguimos energia? Adicionamos energias potenciais de cada carga. Sabemos que a energia potencial de cada carga é uma função de laplaciano zero. Sua soma, portanto, também tem um laplaciano zero. Portanto, a energia potencial de qualquer corpo carregado (não apenas o nosso bastão!) Não pode ter mínimos em um campo elétrico estático!

Conclusão

Imagens intuitivas de campos magnéticos e elétricos de pessoas que não trabalham de perto na física podem ser enganosas. Nosso cérebro nos engana fazendo imagens de mínimos de energia. Infelizmente, não é o caso, e criar um motor Mendocino sem suporte mecânico é muito difícil, se não impossível.

Que brechas existem para explorar? O teorema de Earnshaw (se o aplicarmos a ímãs) se aplica apenas a sistemas de ímãs fixos e estáticos .

1. Podemos criar um campo magnético dinâmico.
2. Diamagnetismo e supercondutores também não se enquadram no teorema de Earnshaw.
3. Corpos móveis (e especificamente rotativos) não são discutidos, o levitron é o exemplo mais famoso.

Não, não é impossível. Certamente, usar qualquer uma dessas brechas mataria a estética de um motor Mendocino, mas a magia de uma coisa de metal levitando livremente superaria tudo isso!

Última observação: foi o teorema de Earnshaw que provou a inexistência de matéria sólida, desmentindo o modelo aceito de um átomo, o que levou ao modelo de átomos “planetário”.