Ao jogar de acordo com as regras padrão do Gomoku, as Pretas não precisam de mais de
35 jogadas para vencer. O artigo apresenta a sua atenção uma estratégia completa de ganhos e o algoritmo correspondente do jogo.
Demonstração da solução completa -
aqui - você pode jogar e encontrar as opções mais longas. O programa sempre vence e gasta nele não mais que 35 jogadas. O código fonte do aplicativo, a solução em si e exemplos de partes no final do artigo.
Não vou me debruçar sobre as regras e táticas do jogo. O tópico foi discutido em detalhes no habr
aqui , bem como algoritmos de decisão
aqui e
aqui .
Pequena digressão
Antes da era dos smartphones, o tic-tac-toe “cinco seguidos” (Gomoku, Renju) era um dos assassinos mais populares da época nas aulas. Considerar combinações foi mais interessante do que o desenvolvimento da economia nacional do norte da África ou a classificação das flores de trevo.
No outono de 1985, meninas da 10ª série foram retiradas de uma aula de matemática. Nós, as seis crianças restantes, é mais provável que tenhamos uma comunicação informal com um professor de matemática sobre tópicos abstratos. O professor entrou na sala de aula em silêncio, distribuiu folhetos para todos em uma caixa e começou a escrever os nomes dos presentes no quadro-negro. Estávamos deprimidos, um trabalho independente ou uma pesquisa blitz foi planejada. Mas a lista no quadro se transformou em uma classificação e fomos anunciados as regras do campeonato. Cada um com cada série de cinco partes. Prêmio ao vencedor - cinco à revista. De acordo com os resultados do torneio, tive a sorte de vencer, mas o jogo não terminou por aí. O professor prometeu fazer cinco anos para todos os rapazes se o vencedor vencer todos os cinco jogos da série consecutivos. O direito do primeiro lance é dado ao vencedor. Ao contrário da afirmação de nosso professor de que, nessa condição, com o jogo certo, você pode ganhar 10, 100 ou qualquer número de jogos consecutivos, a vitória me pareceu uma sorte incrível.
Nove anos depois, em 1994, o Dr. Lewis Victor Allis declarou evidências dessa hipótese em um artigo de
Go-Moku e Threat-Space Search . O autor não publicou sua estratégia vencedora, o que lhe permite verificar a prova. No entanto, em seu livro
Searching for Solutions in Games and Artificial Intelligence , de 1996, foi fornecida uma descrição geral dos algoritmos. Em conclusão, mencionamos separadamente o procedimento para verificar a integridade de uma estratégia vencedora, que se baseia na correção da implementação do algoritmo de busca para a "sequência de ameaças" e na análise das opções de contra-ataque do oponente.
Os exemplos de soluções fornecidas no artigo e no livro com os "movimentos certos" dos oponentes, que fazem parte de uma estratégia vencedora, demonstram a fraqueza do algoritmo usado.

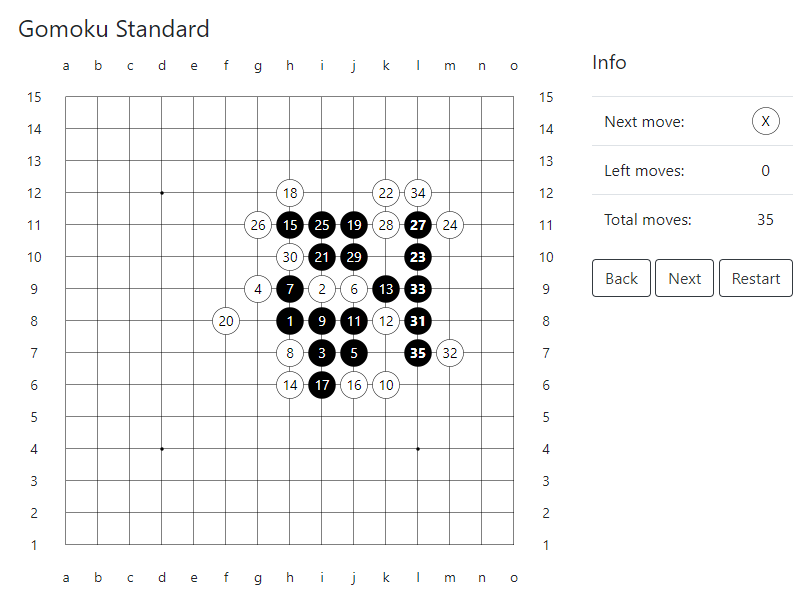
Por exemplo, na figura, a solução do programa para as regras padrão do Gomoku. Se as pretas responderem com j10 e, em seguida, j8 em resposta ao 10º movimento das brancas g9, o jogo termina com 29 movimentos em vez de 45. Então o programa duas vezes "não percebeu" a combinação da "sequência de ameaças" das pretas em 17 movimentos após o 16º e após 26- O movimento das brancas. E no final, se as brancas fizerem a 36ª jogada f12 em vez de j12, ele aguentará pelo menos até a 49ª jogada. Para ser honesto, deve-se dizer que, neste exemplo, todos os movimentos de Black não deixam nenhuma chance de White terminar o jogo a seu favor.
Na Internet, encontrei várias referências a trabalhos semelhantes em busca de uma estratégia vencedora. A questão não resolvida continua sendo a otimização das soluções encontradas. Qual é o número mínimo de jogadas que as pretas precisam para vencer?
Assim, tendo um pouco de tempo livre, recursos modernos de computação e prestando homenagem aos hobbies das crianças 33 anos após o memorável campeonato escolar, ele estabeleceu a tarefa de encontrar a melhor estratégia vencedora para os negros em Gomoku.
Digitalize a posição no quadro
Gravar uma peça é bastante primitivo. Existem apenas 225 células no campo. Assim, cada célula é codificada por 1 byte. Para gravar um lote de 35 movimentos, são necessários apenas 35 bytes. Mas esse registro é pouco adequado para a avaliação de posição por dois motivos: a mesma posição pode ser obtida em uma sequência diferente de movimentos e as posições simétricas não são levadas em consideração.
Atingir o objetivo do jogo - construir cinco pedras seguidas - pode ser realizado em uma de quatro direções: vertical, horizontal e duas diagonais. Assim, podemos representar qualquer posição como um conjunto de linhas. Linhas horizontais e verticais com um comprimento de 15 células e linhas diagonais com um comprimento de 1 a 15 células. Cada movimento altera o valor de 4 linhas em direções diferentes ao mesmo tempo.
A tarefa de avaliar uma posição é determinar todos os números significativos para cada linha. Para simplificar, descrevemos cada célula da linha com 2 bits. O primeiro bit está cheio quando uma pedra branca é instalada, o segundo bit é uma pedra preta. Cada linha contém no máximo 15 células e é codificada em um número inteiro de 32 bits. Assim, a pesquisa de formas em uma linha é reduzida para comparar o valor numérico da linha através de uma janela deslizante com o padrão de bits da forma.

No exemplo mostrado na figura, a posição é descrita por 26 linhas. Por conseguinte, é codificado com 104 bytes, enquanto um registro em lote regular requer apenas 17 bytes.
É fácil adivinhar que todas as simetrias - curvas e imagens no espelho - são obtidas simplesmente alterando o número (embaralhamento) e a direção das linhas. Para identificar uma posição e pesquisar rapidamente coleções, esse princípio implementa uma função hash de 32 bits que fornece valores diferentes apenas para posições assimétricas.
O uso de simetrias reduz significativamente o número de posições consideradas. Por exemplo, o número de opções para o segundo movimento é reduzido de 224 para 35.
Ao procurar soluções e combinações (isso será discutido abaixo), as posições calculadas compõem os vértices do gráfico de multicamadas. Os vértices são agrupados em camadas de acordo com o número de células preenchidas. Os movimentos compõem as bordas do gráfico, conectando os vértices das camadas adjacentes. Quando movimentos malsucedidos são descartados durante a pesquisa, as arestas são excluídas e alguns dos vértices perdem sua conectividade com a ramificação principal. Portanto, após as etapas de cálculo, é realizada a coleta de lixo (ou reconstrução do gráfico a partir do topo).
Durante o processo de desenvolvimento, vários algoritmos de codificação foram considerados, mas o descrito acima mostrou a maior taxa de estimativa de posição.
Avaliar posição
Um fator importante para avaliar uma posição é a importância dos adversários construíram as peças significativas.
Cinco - se uma peça desse tipo for encontrada no tabuleiro, o jogo terminará. Para regras padrão, sem seis, setes, etc., dê um prêmio ao Gomoku. Portanto, os cinco, como, aliás, todas as outras figuras, exigem a ausência de suas pedras nas células vizinhas em uma linha.
 Os quatro abertos
Os quatro abertos - o comprimento de 6 células, os quatro do meio são ocupados por pedras da mesma cor, as externas são necessariamente vazias. Bem, quanto a cinco, suas pedras estão ausentes nas células vizinhas. Uma figura muito forte significa vencer mesmo na jogada de outra pessoa.
 Quatro
Quatro - o comprimento de 5 células, uma (qualquer) das cinco células está livre. Dá uma vitória por conta própria. Isso cria uma ameaça e força o oponente a fazer um movimento em uma célula livre, se ele não tiver seus quatro. Dá 5 pontos na classificação da posição durante a defesa.

 Um triplo aberto
Um triplo aberto - o comprimento de 6 ou 7 células, as células mais externas são necessariamente livres. Para 6 células, três das quatro do meio são ocupadas por pedras da mesma cor, uma livre. Para 7 células - três médias são ocupadas por pedras da mesma cor. Uma peça, por sua vez, torna-se um quatro aberto se o oponente não tiver um quatro ou um três aberto. No movimento de outra pessoa, isso cria uma ameaça e força o oponente a fechar os três ou colocar os quatro em resposta. A sexta célula tripla tem 1 movimento de aumento e 3 movimentos de fechamento. A tripla célula da 7ª célula possui 2 movimentos de aumento e apenas 2 movimentos de fechamento. Dá de 2 a 4 pontos na classificação da posição.


 Um triplo
Um triplo , ou um triplo fechado, é um comprimento de 5 células, três das quais ocupadas por pedras da mesma cor. Os três, por sua vez, podem ser transformados em quatro e são usados em ataque e defesa, criando uma ameaça mais do que um três aberto do oponente. Dá 1 ponto na classificação de posição.


 Um empate aberto
Um empate aberto (em perspectiva) - de 6 a 7 células. Ao atacar, é convertido em três abertos. Dá 1 ou 2 pontos na classificação da posição.


 Um plug
Um plug é ao mesmo tempo duas ou mais ameaças que não podem ser fechadas de uma só vez. Existem garfos de 3x3 (dois triplos abertos), 3x4 (três e quatro abertos) e garfos de 4x4 (dois abertos). Os garfos dão uma vitória se o oponente não tiver uma ameaça maior - quatro ou três abertos para um garfo de 3x3 ou o oponente não pode fechar o garfo sucessivamente, criando grandes ameaças - uma sequência de quatro para um garfo 3x3.



 Combinação
Combinação - uma sequência contínua de ameaças e defesas contra ameaças mais significativas do oponente, levando a um resultado positivo para o jogador. Combinações são atacantes (ou vencedores) e defensivas.
A combinação de ataque ou vitória é bem sucedida se, em qualquer jogada defensiva ou de ataque do oponente, forem encontradas jogadas de resposta que levem à vitória. A combinação de ataque termina com a instalação de um plug, que o oponente não pode fechar.
A combinação defensiva, pelo contrário, é bem sucedida quando o oponente para de criar ameaças ou o limite de movimentos para o cálculo é excedido. Uma combinação defensiva consiste em movimentos defensivos ou na criação de uma ameaça maior ao oponente.
Ao avaliar uma posição, é realizada uma busca por uma combinação vencedora. Se for bem sucedido, vencemos. Caso contrário, se não houver ameaças do oponente, o estado é neutro. Se houver ameaças do oponente, procuramos uma combinação defensiva. Se for bem-sucedido, o estado é neutro; se falhar, perdemos.
Como o número de opções para ataques e retaliações forçadas é bastante limitado, é permitido procurar combinações a uma profundidade suficientemente grande. Durante a construção inicial da estratégia ótima, a profundidade permitida da busca por combinações foi estabelecida em 25 movimentos. Ao recalcular a solução para implementar o algoritmo de estimativa de posição em javascript, a profundidade de pesquisa permitida foi reduzida para 17 movimentos.
Ao calcular a estratégia ideal, a profundidade de pesquisa da combinação vencedora acima foi adicionalmente limitada pelo número máximo alvo de movimentos.
Estamos à procura de uma solução
Portanto, classificamos a posição dada como neutra e escolhemos qual será o próximo passo. Nosso comportamento, neste caso, depende se somos do lado de ataque ou defesa. Para o lado atacante, a solução completa será uma sequência de movimentos em que, para o movimento de retorno de qualquer oponente, a posição é avaliada como vencedora (uma combinação vencedora é encontrada) ou contém o próximo movimento na solução. Vale a pena notar que, para calcular a estratégia ideal, o lado atacante é sempre preto, o lado defensor é branco.
O lado atacante precisa encontrar apenas uma jogada, levando à vitória mais rápida. Nas condições de falta de recursos, o atacante limita artificialmente o número de opções para o rebentamento. Estudo primeiro os movimentos que levam à posição com a pontuação mais alta. Depois que qualquer solução é encontrada, na direção da mais longa delas, o invasor expande o leque de opções, explorando posições menos classificadas para reduzir o comprimento da solução.
É suficiente para o lado defensor encontrar um único movimento que não leve à vitória do oponente no limite de movimentos. Todas as células livres podem ser usadas para enumeração.
Para reduzir o número de movimentos a serem classificados, usamos o algoritmo "pular". Ignoramos a jogada defensiva e procuramos uma combinação de ataque vencedora. Se for bem-sucedido, os possíveis movimentos de defesa podem ser limitados aos movimentos que afetam o sucesso da combinação encontrada. Em média, em cada etapa, isso permite reduzir a área de pesquisa em 4-6 vezes. Observe que entre os movimentos ignorados, pode haver ramificações mais longas da solução. Portanto, para procurar soluções ideais, o algoritmo “pular” é usado apenas na pesquisa inicial.
Nós calculamos a estratégia
Todos os componentes estão prontos, colocamos a primeira pedra preta no centro do campo, iniciamos a busca por uma solução e ... Com isso, depois de algumas horas, os recursos do meu laptop acabam e eu tenho que admitir a derrota "em batalha, mas não em batalha".
Na verdade, eu tinha na ponta de meus dedos o poder de computação com uma centena e meia de núcleos Xeon e um terabyte de RAM livre. Mas lembre-se de que, em meados dos anos 90, a Allis possuía apenas 10 SUN SPARCstation 2 em 128 MB de RAM, sentiu remorso por comportamento antidesportivo e decidiu limitar a quantidade de RAM na máquina java a 1 GB e alocou apenas 1 thread para a tarefa o processador. De alguma forma, poderia compensar meu GHz em comparação com seu MHz. Além disso, ele prometeu a si mesmo, no final do trabalho, transferir os algoritmos para o javascript do navegador.
Assim, a busca de estratégias teve que começar com a decisão dos esboços de estreia. Uma descrição detalhada das estreias do jogo Renju em russo pode ser encontrada nos famosos livros de Sagar "From Debut to Middlegame" e Mikhail Kozhin e "Ringing of the Stones" de Alexander Nosovsky
aqui . Os livros já têm 20 anos, mas desde então um pouco dessa literatura foi publicada. A coleção mais recente de Dmitry Epifanov “Tiger in a cage” de 2015, infelizmente, não está disponível em formato eletrônico.
A busca por decisões ótimas de abertura foi realizada de acordo com o seguinte algoritmo. Na primeira etapa, um cálculo preliminar foi realizado sem limitar a duração do lote. Em seguida, para as soluções mais longas, foi realizada a otimização: substituindo as combinações encontradas por soluções mais curtas para as etapas finais e procurando ramificações de decisão mais curtas para todos os movimentos intermediários. A otimização foi realizada até que o limite de destino fosse atingido para todas as ramificações da solução. Em seguida, o limite de destino diminuiu e foi feita uma tentativa de otimizar para um novo valor.


Não houve problemas com a 3ª estréia vertical na Figura 3. O resultado foi um conjunto completo de soluções. As posições mais difíceis após a quarta jogada i8 e j10 foram resolvidas em 31 jogadas. Em seguida, foi definido um limite de 35 jogadas por jogo.


Na diagonal da decisão, ele tradicionalmente escolheu a 7ª estréia. A posição mais difícil surge após o 4º passo g9. Foram encontradas soluções de comprimento admissível para 6 movimentos g8 e g7.

Mas para esta opção, com o sexto movimento no j9, não consegui encontrar uma solução menor que 33 movimentos. Foi quase um desastre. Desesperado, tentei as soluções para a 5ª jogada alternativa, bem como todos os outros tipos de aberturas diagonais. As estreias foram resolvidas até o final, mas não foi possível encontrar nada menor que 39 movimentos por jogo.
Retornando à 7ª estréia diagonal original, ele refez o algoritmo para gerar sentenças para ataques de ataque. Como resultado, movimentos que levaram a posições com uma pontuação de classificação dos terceiros dez inesperadamente começaram a dar um resultado e reduzir o comprimento do caminho da solução. A variabilidade do cálculo com tal quantidade tornou-se bastante grande. Com uma profundidade de solução de 12 movimentos, havia mais de 2 milhões de posições (excluindo posições ao procurar combinações). A continuação repousou em 1 GB de RAM alocada para a tarefa. Assim, para verificar a decisão do garfo final, em alguns casos foi necessário decidir separadamente as posições da 18ª jogada.
Depois que a 7ª estréia na diagonal foi decidida em 35 movimentos, era possível comemorar a vitória - a luta pelo centro foi vencida. Ainda havia uma enorme quantidade de trabalho computacional de rotina, cálculos de movimentos brancos “não ótimos” para concluir a estratégia. Do volume total da estratégia ideal, a resposta para esses movimentos foi de 80%. Felizmente, eles foram resolvidos automaticamente completamente no cálculo preliminar após o segundo movimento, e todo esse volume foi adicionado à estratégia ideal em alguns dias.
Portanto, foram encontradas soluções para todos os 2 movimentos. Colocamos a primeira pedra preta no centro do campo, iniciamos a busca por uma solução e nem sequer temos tempo para sentir a importância do momento - a posição inicial foi resolvida em 35 movimentos. O gráfico da melhor estratégia vencedora é construído.
Verificando a nós mesmos
O próximo passo é verificar a solução. Desligue completamente a inteligência do lado defensor. Após cada jogada de preto, o branco vai para qualquer quadrado livre do tabuleiro. A posição obtida após a jogada de White deve ser encontrada no gráfico de decisão ou avaliada como vencedora pelo número de jogadas que não excedem o maior ramo na posição inicial. Ao avaliar cada posição, verificamos a combinação vencedora encontrada para todos os movimentos admissíveis das brancas antes das pretas construírem a peça final - cinco seguidas.
A verificação foi realizada várias vezes até a conclusão. A execução final sem erros no modo de thread único levou 14 horas. No decorrer da verificação, foram encontrados e corrigidos erros que surgiram como resultado de diferenças na profundidade da busca por combinações, suposições para pular, duplicação de posições simétricas.
Responda à pergunta - a decisão em 35 movimentos é realmente a mais ideal. De acordo com minha pesquisa, para vários ramos mais longos da estreia vertical, é possível encontrar soluções mais ideais com 33 movimentos. Mas para a diagonal após o sexto movimento no j9, muito tempo foi gasto na busca de uma solução em 33 movimentos, a variação do preto expandida para 50 movimentos em cada etapa e sem sucesso. Não é possível provar rigorosamente a falta de solução em 33 jogadas, o tempo alocado para o projeto chegou ao fim e foi tomada uma decisão para parar no limite de 35 jogadas.
Converter de java para javascript
A publicação de uma solução para um problema requer clareza.
Para usar a solução diretamente no navegador, foi necessário:- Reduza a profundidade da busca por combinações ao avaliar posições para 17 movimentos. Isso levou a um aumento de 2-3 vezes no número de movimentos calculados da estratégia ideal.
- Converta o formato de gráfico de decisão binária em sequência de movimentos JSON. Este formato é mais conveniente em javascript e visual.
- Converta classes java em módulos javascript, exceto para procedimentos de tomada de decisão. Aqui, na interface da Web, substitua as chamadas do serviço de descanso por funções locais.
Lista de classes de aplicativos:- Conselho - gerenciamento de parte no conselho, interface visual
- Vértice - gráfico no topo da decisão, herdado da posição
- Borda - borda do gráfico de decisão, move as posições de conexão
- Layout - posição, contém uma coleção de linhas
- Linha - uma linha em uma determinada direção, contém uma coleção de formas
- Figura - uma figura que determina o tipo e o início de uma figura em uma linha
- Padrão - padrões de figuras para comparação ao pesquisar
A solução completa no formato JSON pode ser baixada do arquivo gomoku.json .Fontes no repositório no GitHub .Para maior clareza, darei exemplos abaixo dos jogos mais longos obtidos na demonstração clicando em Avançar.Estreia na diagonal:
 Estreia na vertical:
Estreia na vertical:
