Níveis de dificuldade de leitura
Introdução e regras do jogo
Alguns anos atrás eu comprei o jogo Dobble ( Dobble , o nome original é "Spot It!"). Este é um jogo muito simples, rápido e divertido, que considero um dos melhores jogos de tabuleiro em geral.
Existem 55 cartas no jogo com 8 símbolos diferentes em cada uma. Veja como são esses cartões:

Fig. 1. Um exemplo de um cartão de jogo.
Em cada duas cartas, um e apenas um símbolo corresponde. Na figura acima, este é um símbolo a lápis:

Fig. 2. Caracteres correspondentes nos cartões.
O jogador que viu a partida pela primeira vez faz uma ação em uma das cartas, dependendo da rodada do jogo. Por exemplo, leva para si mesmo ou joga para um oponente.
Muitas vezes, isso leva ao fato de que uma das cartas pelas quais os jogadores procuram partidas está mudando. Por isso, é necessário procurar uma nova correspondência, que pode ser um símbolo completamente diferente:


Fig. 3, 4. O primeiro cartão é substituído por um novo. Agora há uma nova coincidência entre eles - o símbolo do palhaço.
Como eles fazem isso?
À primeira vista, parece inacreditável que em duas cartas exatamente uma coincidência, nem mais nem menos. As perguntas surgem imediatamente - quantos personagens existem no jogo? Eles não podem ser muito poucos (então haverá mais de uma correspondência nas cartas) ou muito (então pode não haver correspondências nas cartas).
Além disso, é óbvio que os símbolos estão localizados nas cartas em uma ordem especial, o que garante a única correspondência entre duas cartas.
As habilidades básicas do Google nos levam ao site stackoverflow, que descreve por que isso acontece: http://stackoverflow.com/questions/6240113/what-are-the-mathematics-computational-principles-behind-this-game
O jogo usa os princípios da geometria finita . Embora exista a palavra "geometria" nesta frase, esse conceito se refere mais à combinatória do que à geometria. Opera com um número finito de pontos que podem ser localizados, em particular, na forma de um plano projetivo .
Cartas e símbolos no jogo são elementos do plano projetivo da 7ª ordem. Isso significa que em cada carta existe um símbolo n + 1 e o número total de símbolos únicos no jogo é n ^ 2 + n + 1 , ou seja, 57 caracteres.
Existem planos de ordens inferiores e superiores. Por exemplo, existe um plano de 5ª ordem. Para ela, 6 símbolos são mostrados no cartão e o número total de símbolos únicos no jogo é 5 ^ 2 + 5 + 1 = 31. O plano projetivo dessa configuração é usado em uma versão mais simples do jogo Doble chamada “Doble 1,2,3” .
A conexão entre pontos e linhas para o plano projetivo é definida usando a matriz de incidência . Sua aparência é apresentada na seção “Matriz de incidência do jogo Dobble”.
Geometria final para bebês
Muito depois de escrever o artigo original, assisti a uma palestra de Alexei Savvateev , onde ele falou sobre geometria projetiva muito mais curta e mais compreensível. Mas como não tenho força ou desejo de reescrever metade do artigo por causa disso, apenas recomendo seu livro "Matemática para Humanidades", se minha tentativa do selvagem de explicar o dispositivo do carro nos dedos fosse incompreensível ou chata.
Primeiro, vá à Wikipedia e leia alguns artigos. O primeiro artigo descreve o conceito de geometria finita:
Uma geometria finita é qualquer sistema geométrico com um número finito de pontos . [1]
Até agora, tudo é simples. Se você desenhar vários pontos com uma caneta no papel, eles já formarão algum tipo de geometria finita.
Uma surpresa aguarda muito mais:
Por exemplo, a geometria euclidiana não é finita, pois a linha euclidiana contém um número ilimitado de pontos, ou melhor, contém exatamente quantos pontos há números reais . [1]
Para nós, isso significa que o pedaço de papel no qual nossos pontos são desenhados não é um plano em termos de geometria finita . É apenas uma portadora de pontos.
Existem dois tipos de geometria no plano: afim e projetiva . Na geometria afim, é usada a noção usual de paralelismo de linhas. [1]
Lembre-se de que axiomas descrevem geometria afim:
A geometria afim em um plano é um conjunto não vazio X (cujos elementos são chamados de "pontos"), com uma coleção não vazia de subconjuntos L de X (cujos elementos são chamados "diretos"), de modo que:
- Para dois pontos diferentes, há apenas uma linha que contém os dois pontos.
- Para uma linha ℓ e um ponto p não pertencente a ℓ , existe uma e apenas uma linha containing ℓ contendo p, de modo que ℓ ∩ ℓ ′ = ∅.
- Existem muitos dos quatro pontos, nenhum dos quais está na mesma linha. [1]
Esses axiomas nos dão a oportunidade de entender como é o plano afim mais simples na geometria finita:
O plano afim mais simples contém apenas 4 pontos e é chamado de plano afim de segunda ordem . Cada par de pontos define uma linha única; portanto, o plano indicado contém 6 linhas. [1]
Não está muito claro? Isso mesmo. Se você olhar atentamente para a definição de geometria afim, poderá ver que ela opera com os conceitos da teoria dos conjuntos (elemento, conjunto, subconjunto).
Isso significa que as linhas podem não se parecer com as linhas usuais da geometria euclidiana.
De fato é. Se você olhar a figura do plano afim de segunda ordem, veremos a figura a seguir:

Fig. 5. plano ateniense de segunda ordem. (Fonte ru.wikipedia.org )
Os pontos aqui parecem pontos pretos comuns, mas as linhas retas são segmentos multicoloridos. Linhas da mesma cor são consideradas paralelas.
Como você pode ver, as linhas aqui não são de tamanho infinito. Em segredo, direi que não há nenhum conceito de comprimento aqui, e as linhas retas podem ter qualquer forma, como veremos em breve.
Certamente% username% ainda duvida que a imagem deste plano satisfaça os axiomas da geometria afim. Vamos verificar:
- Tomamos 2 pontos, por exemplo, no canto superior esquerdo e no canto inferior esquerdo.
Ambos os pontos contêm apenas uma linha vermelha esquerda.
A linha vermelha direita não contém nenhum desses pontos e as linhas restantes contêm apenas um deles. - Pegue a linha reta vermelha esquerda e o ponto superior direito. Obviamente, apenas uma linha reta (vermelho à direita) é paralela à linha vermelha esquerda, pois passa pelo ponto superior direito, mas não passa por nenhum dos dois pontos esquerdos.
- A figura mostra claramente que, independentemente dos três pontos que anotamos, um deles fica em uma linha diferente da linha em que os outros dois pontos estão.
As duas linhas que formam as diagonais de um quadrado não se cruzam, pois não possuem pontos em comum.
Se você entendeu bem o conteúdo da imagem anterior, a imagem é mais complicada:
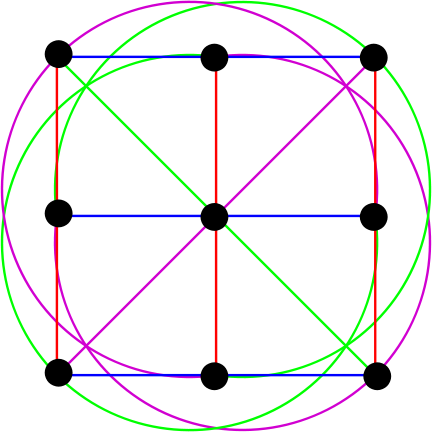
Fig. 6. Plano ateniense de terceira ordem. (Fonte ru.wikipedia.org )
Aqui vemos 9 pontos e 12 linhas. Sim,% username%, essas elipses são na verdade linhas retas em termos de geometria finita.
Formas da mesma cor são linhas paralelas. Como é difícil perceber, dividimos a imagem em várias:
| Avião número 1 | Avião número 2 | Avião número 3 | Avião número 4 |
|---|
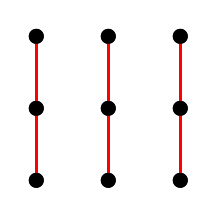 | 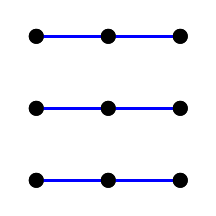 |  |  |
Fig. 7. Linhas retas paralelas do plano afim de terceira ordem.
Aqui, a verificação da execução dos axiomas levará um pouco mais de tempo:
- Tomamos 2 pontos, por exemplo, no canto superior direito e no canto inferior direito. Através deles passa apenas uma das linhas roxas.
- Pegue a linha vermelha esquerda e o ponto inferior direito. Da mesma forma que um plano de segunda ordem, apenas uma linha vermelha direita passa por esse ponto, mas não passa por nenhum dos três pontos esquerdos.
- Aqui é um pouco mais complicado do que no caso de um avião de 2ª ordem. A declaração do axioma diz que você precisa encontrar pelo menos um conjunto (não vazio) de quatro pontos, nos quais não existem três em mais de uma linha.
Obviamente, 12 séries com três pontos através dos quais as linhas da figura passam não satisfazem essa condição. Mas satisfaz, por exemplo, um conjunto de quatro pontos de canto.
Em um caso mais geral, um plano afinado finito de ordem n tem n ^ 2 pontos en ^ 2 + n linhas; cada linha contém n pontos e cada ponto pertence a n + 1 linhas. [1]
Com a geometria afim finalizada, passamos para o segundo tipo de geometria no plano - projetivo.
Na geometria projetiva, pelo contrário, quaisquer duas linhas se cruzam no único ponto possível e, portanto, linhas paralelas não existem. [1]
A frase anterior descreve o segundo axioma da geometria projetiva. O primeiro e o terceiro são os mesmos do ateniense.
Como o terceiro axioma requer a existência de pelo menos quatro pontos, o plano deve conter pelo menos 7 pontos para satisfazer as condições dos dois primeiros axiomas. Neste mais simples dos planos projetivos, há também 7 linhas; cada ponto pertence a três linhas e cada linha contém três pontos. Esse plano projetivo costuma ser chamado de "plano Fano" . [1]
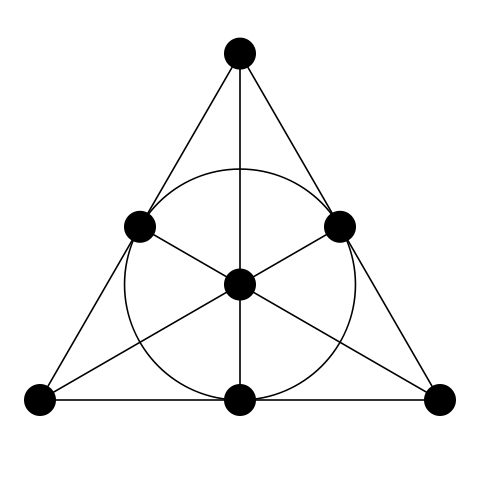
Fig. 8. avião Fano. (Fonte en.wikipedia.org )
Nesta figura, é difícil entender imediatamente todas as 7 linhas, então aqui está uma versão pônei do mesmo plano:
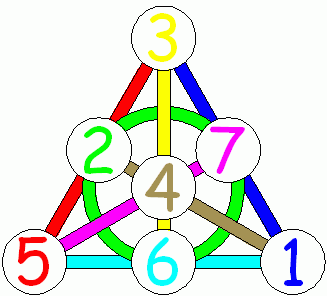
Fig. 9. avião Fano com linhas coloridas. (Fonte mathpuzzle.com . Usado com permissão de Ed Pegg Jr. )
Portanto, o plano Fano é um plano projetivo de 2 ordens com 7 pontos e 7 linhas.
O que o cartão tem a ver com isso?
O que acontece se reformularmos 2 axiomas de geometria finita , substituindo a “linha” pelo “símbolo” e o “ponto” pelo “cartão”?
O resultado é este:
- Para duas cartas diferentes, existe apenas um símbolo, que é mostrado nas duas cartas.
- Para dois símbolos diferentes, há apenas um cartão que contém esses dois símbolos.
Agora, com base nesse conhecimento, vamos ver como seria o Dobble no caso mais simples. Teria 7 cartões e 7 caracteres, cada cartão teria 3 caracteres (como 3 linhas se cruzam em um ponto):
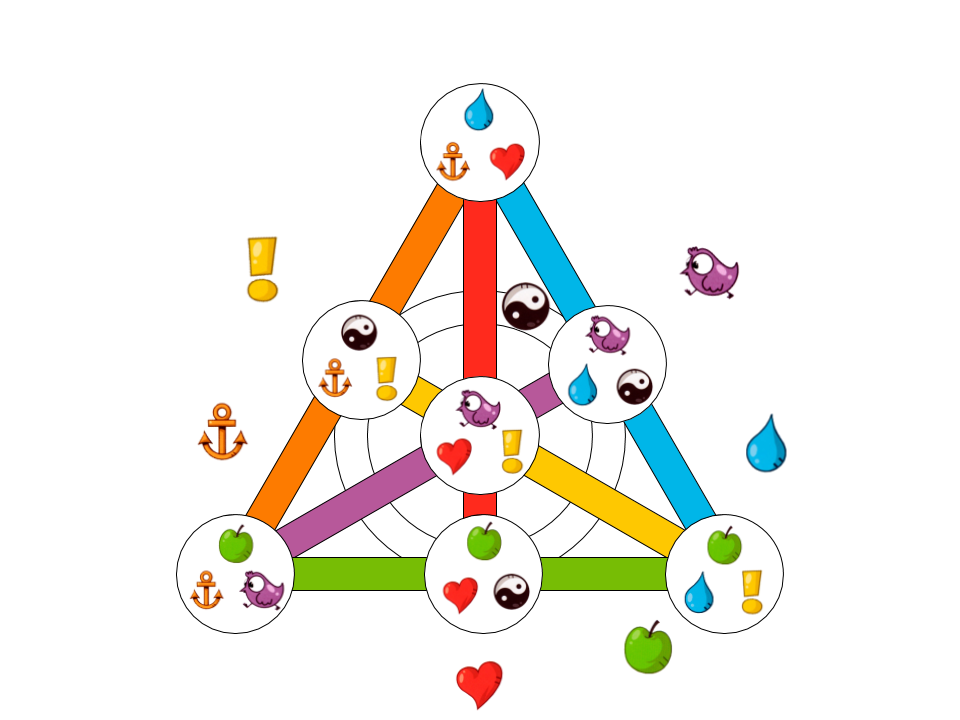
Fig. 10. Um exemplo do menor conjunto de cartas possível para Dobble.
Os 7 caracteres a seguir são usados aqui:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Independentemente das duas cartas que recebermos, elas terão um símbolo comum, representado ao lado da linha em que ambas as cartas estão.
Por exemplo, o cartão no canto inferior esquerdo e o cartão no meio do lado direito têm um símbolo comum  . É mostrado ao lado da linha.
. É mostrado ao lado da linha.  .
.
Aviões projetivos de pequenas encomendas
No Wolfram, você pode encontrar uma demonstração visual de planos projetivos de pequenas encomendas: http://demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
Ele foi projetado como um documento no formato CDF (formato de documento computável), para o qual você precisa instalar o CDF Player .
Aqui está um exemplo de um plano projetivo de ordem 3:
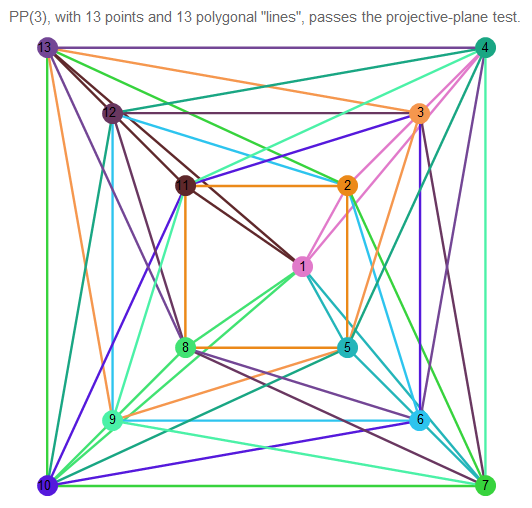
Fig. 11. Imagem do plano projetivo de 3 ordens.
É difícil entender o que está acontecendo, portanto, escolha 2 linhas arbitrárias:
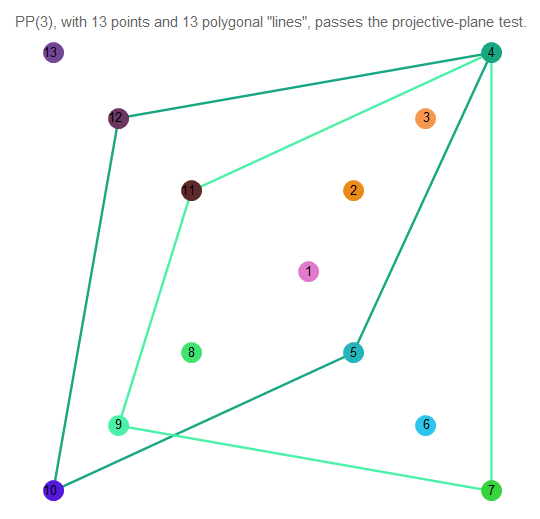
Fig. 12. A interseção de duas linhas do plano projetivo de 3ª ordem.
Como vemos, eles se cruzam exatamente em um ponto. As próprias linhas contêm 4 pontos.
Para garantir que 4 linhas passem por cada ponto, é necessário alternar os pares de linhas exibidos em um documento interativo e focar em algum ponto.
Os planos projetivos de pedidos mais altos são mostrados nas figuras abaixo.
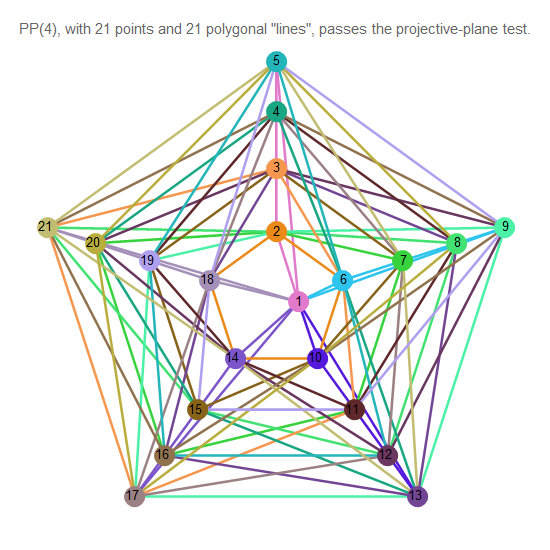
Fig. 13. Plano projetivo de ordem 4
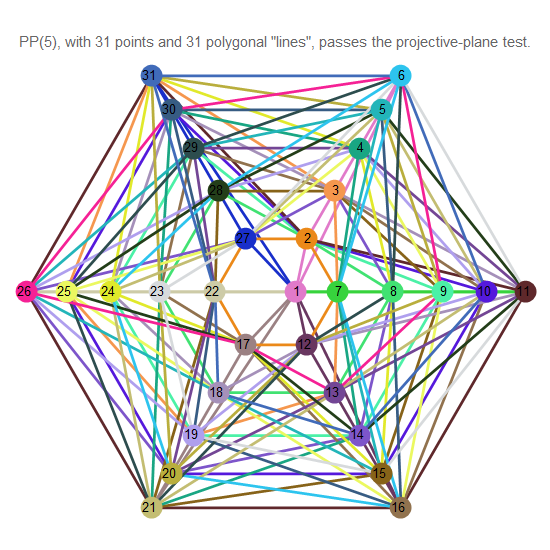
Fig. 14. O plano projetivo de ordem 5

Fig. 15. Plano projetivo de ordem 7
Na sequência acima, não há imagem para o plano projetivo de 6ª ordem. Isto não é um erro.
Embora Wolfram gere uma representação gráfica dessa estrutura, ele não satisfaz os axiomas da geometria projetiva e não é um plano projetivo.
Supõe-se, mas ainda não está provado, que a ordem de um plano finito é sempre uma potência principal . [1]
Como construir um plano projetivo?
A representação gráfica do plano projetivo parece interessante e clara, mas como encontrar essa combinação de pontos para que possua as propriedades acima?
A maneira mais fácil é visitar sites que hospedam dados pré-calculados para planos projetivos de vários pedidos.
Por exemplo, para o plano projetivo da ordem 7, você pode visitar a seguinte página: https://web.archive.org/web/20170619110638/https://www.uwyo.edu/moorhouse/pub/planes/pg27.txt
Uma matriz de números é apresentada lá. Linhas são cartões (pontos) em termos de Dobble. Os números nas linhas são os números de série dos caracteres (linhas), começando do zero, que são desenhados em cada cartão (passam por este ponto).
Você também pode usar os serviços de pacotes matemáticos, como o Matlab, para construir a matriz de incidência do plano projetivo. [2] [3]
Matrizes de incidência
A matriz de incidência é uma das representações do gráfico que indica as relações entre os elementos incidentes do gráfico (aresta (arco) e vértice). As colunas da matriz correspondem às arestas, as linhas aos vértices. Um valor diferente de zero na célula da matriz indica a relação entre o vértice e a aresta (sua incidência ). [2]
Um dos exemplos mais simples da matriz de incidência pode ser uma matriz 2x1 para um gráfico não direcionado de dois vértices conectados por uma aresta:

Fig. 16. Um gráfico não direcionado de dois vértices conectados por uma aresta e sua matriz de incidência.
Um exemplo mais complexo de um gráfico e sua matriz de incidência:
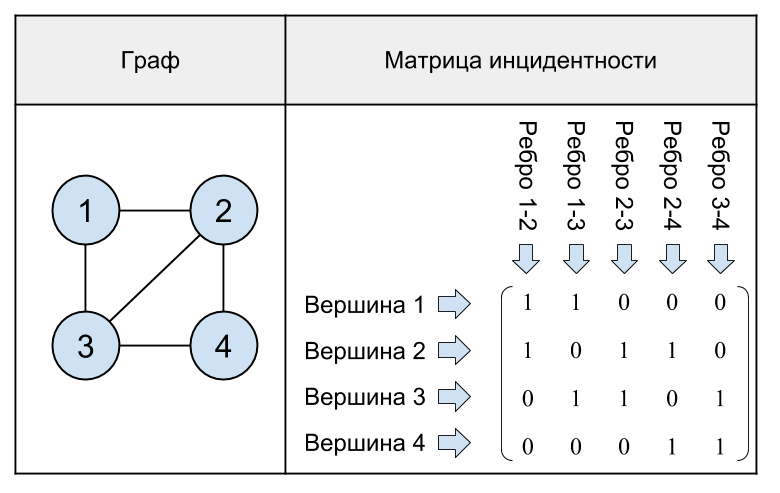
Fig. 17. Um gráfico não direcionado com 4 vértices e sua matriz de incidência.
Como pode ser visto no último exemplo, na matriz de incidência do gráfico em cada coluna há exatamente duas unidades, porque uma aresta conecta dois vértices.
O plano projetivo é um hipergrafo , pois uma linha (aresta) conecta vários pontos (vértices). Portanto, na matriz de incidência do plano projetivo, as unidades em cada coluna ocorrem n + 1 vezes, onde n é a ordem do plano projetivo.
Para o plano Fano mostrado na Fig. 9, a matriz de incidência será a seguinte:

Fig. 18. A matriz de incidência do plano Fano.
Para simplificar a percepção, os zeros não são mostrados e as unidades são substituídas pelo símbolo X.
Nesta representação do plano projetivo, o princípio da dualidade de pontos e linhas é claramente visível - a linha passa exatamente por 3 pontos e, ao mesmo tempo, o ponto pertence exatamente a três linhas.
Construindo um plano projetivo por força bruta
O conhecimento atual sobre as propriedades da matriz de incidência é suficiente para construí-la para o plano projetivo de qualquer ordem n. Para fazer isso, você pode usar o seguinte pseudocódigo:
n+1 , n+1 , ,
Seguindo esse algoritmo, obtemos uma matriz simétrica para o plano de Fano:

Fig. 19. A matriz de incidência do plano Fano construída pelo algoritmo de pseudo-código.
Essa matriz não corresponde à anterior. Na verdade, isso não importa.
A permutação de quaisquer duas linhas da matriz de incidência é equivalente a renumerar os vértices do gráfico.
A permutação de quaisquer duas colunas da matriz de incidência é equivalente a renumerar as arestas do gráfico (se elas forem numeradas antecipadamente).
Matriz de Incidentes para Dobble
Para o jogo Dobble na matriz de incidência, as linhas são responsáveis pelas cartas e as colunas são responsáveis pelos personagens nelas.
Assim, a permutação de quaisquer duas colunas da matriz de incidência é equivalente a uma alteração na sequência de caracteres do cartão. No entanto, os símbolos no cartão não são ordenados, portanto, esta operação não afeta a aparência dos cartões.
Reorganizar duas linhas significa que em todas as placas dois símbolos correspondentes se substituem.
A última operação muda a aparência das cartas, o que significa que o conjunto de personagens que vemos no jogo é apenas uma das combinações possíveis.
O número de conjuntos de caracteres para uma determinada carta é uma combinação de 57 elementos e 8 elementos sem repetição. É calculado pela fórmula 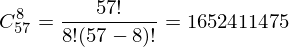
A matriz de incidência para Dobble é mostrada na tabela abaixo. É transposto, ou seja, linhas são símbolos e colunas são cartões (a imagem é clicável). O Habr não permite que você insira uma imagem do tamanho e qualidade desejados; portanto, a opção de tamanho completo é um link separado: https://github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble%20incidence%20matrix.png

Fig. 20. A matriz de incidência do jogo Dobble.
Quais são as duas cartas que faltam no jogo?
No total, a tabela com a matriz de incidência do jogo possui 57 linhas e 55 colunas. Isso significa que o jogo pode ter mais 2 cartas.
Isso significa que os personagens que devem estar nessas cartas são menos comuns no jogo do que os demais. O número de personagens no jogo é mostrado na última coluna da tabela.
O número de caracteres dos cartões ausentes é o seguinte:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  e
e 
(Total de 14 caracteres) ocorre 7 vezes. ocorre 6 vezes.
ocorre 6 vezes.
Como são os cartões ausentes? Para responder a essa pergunta, pegue um dos caracteres acima na matriz de incidência (exceto o boneco de neve) e coloque-o no cartão que está faltando (por exemplo, a penúltima coluna).
Em seguida, encontramos todas as cartas (colunas) nas quais esse símbolo é representado. Isso significa que em todas essas cartas os símbolos coincidem e não pode haver outras correspondências.
Como essas cartas já coincidem com o personagem selecionado, cruze da penúltima coluna todos os caracteres que aparecem nas outras cartas.
Personagens ausentes que não foram eliminados e compõem os personagens de uma das cartas restantes. Como eles acabaram sendo exatamente 8, o tipo do segundo cartão ausente é determinado sem ambiguidade.
Aqui estão estes 2 cartões:


Fig. 21. Um tipo possível de cartão ausente é o número 56 e o número 57.
Resta responder à última pergunta - a ausência dessas cartas afeta a propriedade de coincidência de um único símbolo entre duas cartas (ou seja, de repente não há correspondências entre algumas cartas)?
A resposta é óbvia, se você ainda olha para a matriz de incidência do jogo - não, não é. Entre duas cartas (colunas) ainda é a única coincidência.
Por que existem 2 cartas abaixo do máximo possível no jogo?
Inicialmente, as regras para os cinco mini-jogos não estavam no livreto, mas em cinco cartas separadas. Ao mesmo tempo, apenas 60 cartões podem ser impressos. Portanto, os autores do jogo decidiram remover 2 cartas, de modo que no final foram 55 cartas com símbolos + 5 cartas com regras. (Agradecimentos especiais a Guillaume Gille-Naves pelo esclarecimento.)
Agradecimentos
Expresso minha gratidão à rede de lojas de jogos de tabuleiro "Igroved" por sua ajuda na redação do artigo.
Agradecimentos a Ed Pegg Jr por fornecer a imagem do avião Fano.
Separadamente, quero mencionar um anonymus e Master para ajudar na verificação do artigo.
Agradeço à loja "Table City" por sua ajuda na preparação para a publicação do artigo.
De todo o coração, agradeço aos autores do jogo Igor Polouchine, Denis Blanchot, Guillaume Gille-Naves e Asmodee pelo direito de usar imagens do jogo.