Ternário equilibrado
Estou trabalhando nas aulas de princípios de arquitetura de computadores da nossa universidade; e, como tarefa, gostaria de propor aos meus alunos a construção de uma máquina programável simples que funcione no ensino médio. A principal razão é divertida: como palestrante, devo trazer um pouco de entretenimento, caso contrário não serei ouvido. Além disso, é importante por razões históricas. Mais algum "por que ?!" as perguntas serão respondidas "Porque eu posso".
Esta página descreve o básico, não vai além de um simples somador ternário (e sua implementação de hardware). Fique ligado para mais.
Escolhi o sistema ternário equilibrado: cada trit representa um dos três estados possíveis, -1, 0 ou 1. Uma descrição muito extensa desse sistema pode ser encontrada
aqui .

O componente básico: multiplexador ternário
Abstração
O único bloco que será usado no meu computador é o multiplexador ternário.
Pode ser vista como uma caixa preta com cinco pinos: o pino seletor recebe um sinal ternário (-1, 0 ou 1) e, em seguida, há uma pequena chave dentro da caixa que conecta o pino de saída a um dos três pinos de entrada inN, inO ou inP.
Geralmente é descrito como mostrado aqui:
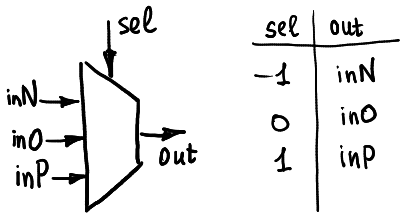
O desmultiplexador ternário funciona da mesma maneira: dependendo do pino seletor, uma entrada é conectada a um dos três pinos de saída possíveis. Observe que no meu hardware eu uso comutadores analógicos CMOS. Como são bidirecionais, o hardware pode ser usado como multiplexador e desmultiplexador. De qualquer forma, por enquanto não uso possibilidades de desmultiplexação.
Implementação de hardware
O projeto básico foi proposto por
Shaos .
A única coisa que fiz foi criar a versão SMD do TRIMUX. Os interruptores de montagem em superfície dg403 podem ser comprados por 50p por peça na China.
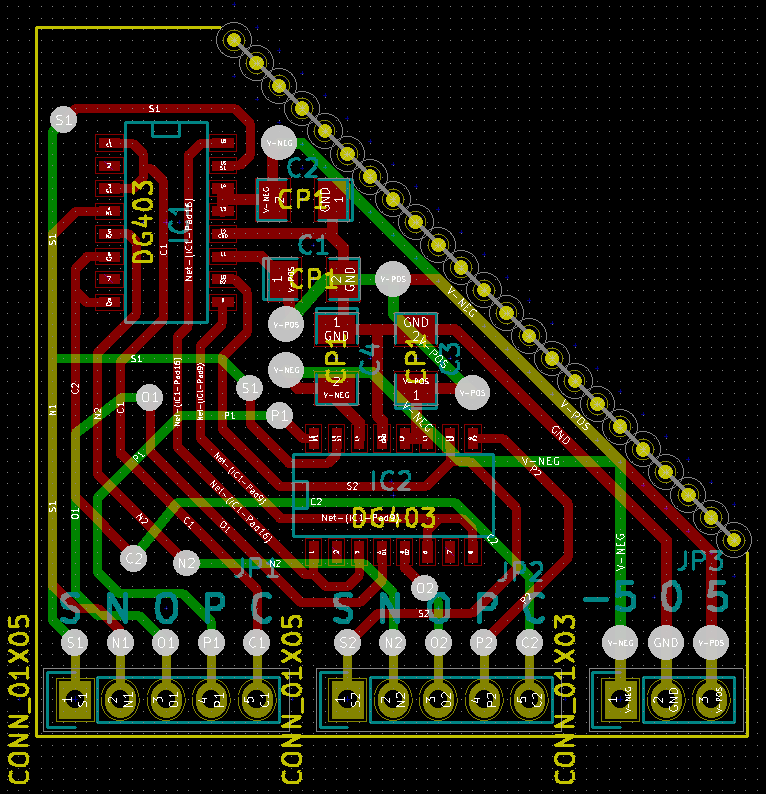
Antes de encontrar esse design, tentei usar combinações de cd4007 e cd4016. Funcionou, mas o hardware é pesado e feio. Os comutadores DG403 fornecem verdadeiras possibilidades de computação ternária sem redundância, como usar binário de dois bits e banir uma das quatro configurações.
Um multiplexador ternário pode ser criado com dois DG403: um dos ICs recebe entrada de energia de -5V a 0V, enquanto o outro é alimentado com 0V a 5V, e permite o uso de sinais ternários representados por três tensões -5V, 0V e 5V, respectivamente. Esse design usa apenas metade dos pinos do dg403; portanto, é natural criar uma placa com dois multiplexadores.
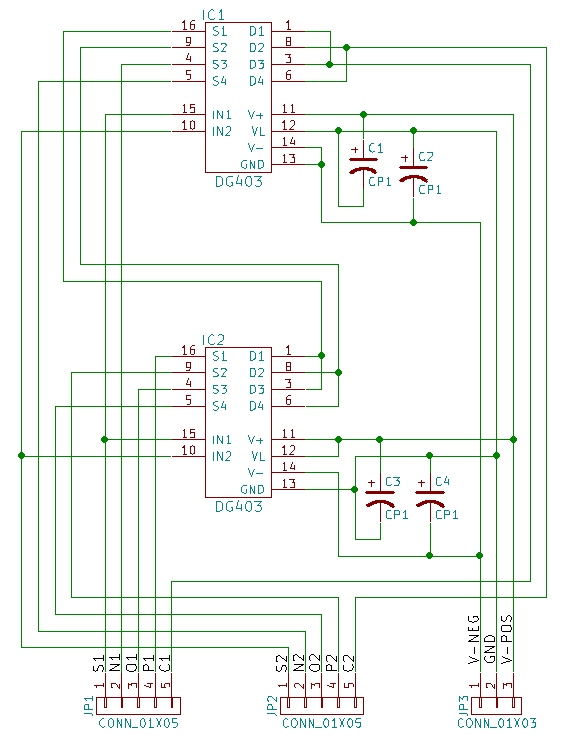
Não hesite em entrar em contato com Shaos
aqui . Cara incrível, em vez de especular sobre os benefícios do ternário, ele projetou e fabricou seus próprios CIs ternários!

Como usá-lo? Funções unárias
Vamos omitir a função de identidade que podemos obter dando -1,0 e 1 aos pinos de entrada correspondentes do multiplexador.
Para o início, vamos incrementar o sinal de entrada A calculando A + 1 (é claro, no anel -1,0,1):
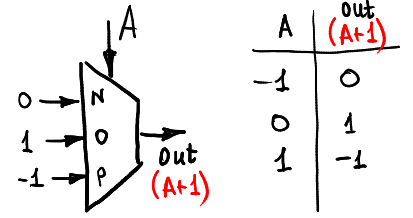
Aqui está a maneira pela qual podemos diminuir a entrada:
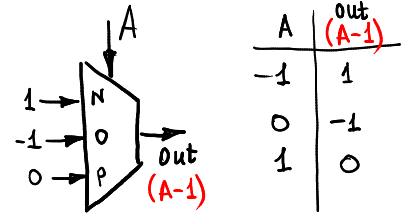
Vamos calcular max (A, 0):
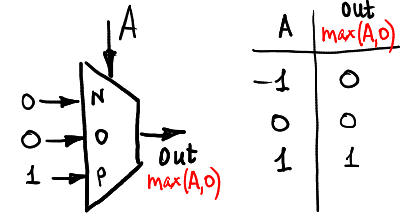
E o mínimo (A, 0):
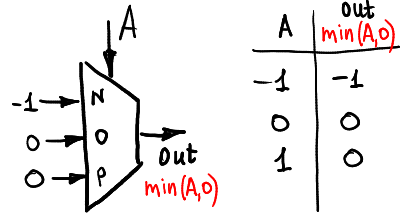
Funções de dois argumentos: meio-somador
A + B
Portanto, um multiplexador nos permite calcular qualquer função unária. Para calcular uma função de dois argumentos, precisamos usar três ou quatro multiplexadores. Por exemplo, se quisermos calcular uma soma de dois sinais A e B (ainda no anel -1,0,1), poderemos usar este esquema:
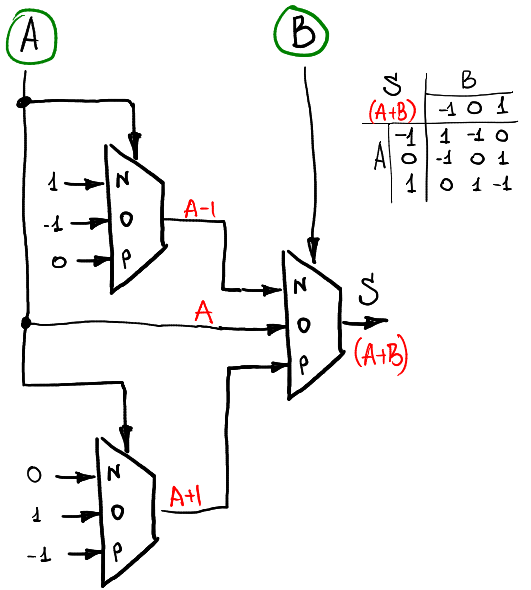
Existem duas camadas de multiplexadores: a primeira calcula funções unárias de A e a segunda camada as combina de acordo com B.
Consenso
Se quisermos calcular a função de consenso de dois sinais ternários (consenso é igual a -1 se A = B = -1, é igual a 1 se A = B = 1 e é zero caso contrário), podemos fazer o seguinte:
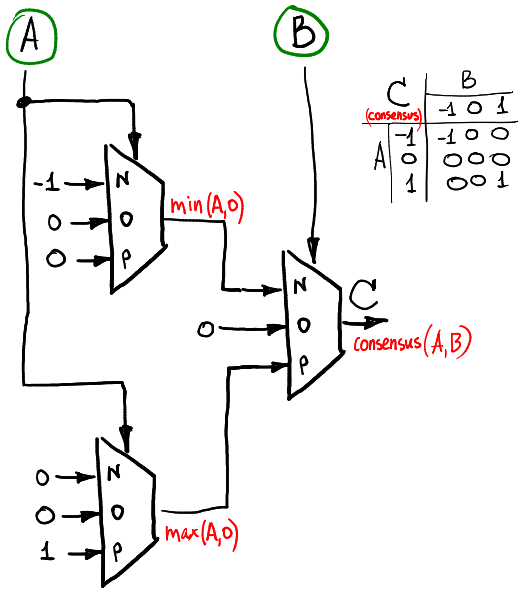
Implementação de hardware
De fato, acabamos de criar
uma meia-somadora . Para duas entradas A e B calcula duas saídas S e C relacionadas como A + B = S + 3 * C. S é a soma e C é a bandeira de transporte.
Vamos testar o design! LED vermelho significa -1, desligado significa 0, LED verde significa 1. Portanto, esta foto nos diz que S = -1, C = 1 ou, em outras palavras, 1 + 1 = -1 + 3 * 1:

Aqui está a tabela que lista todos os nove estados possíveis do nosso meio-somador. Cada célula fornece valores correspondentes para S e C. Um link para uma foto é fornecido para cada célula.
| S, c | B |
| -1 | 0 0 | 1 |
| Um | -1 | 1, -1 | -1,0 | 0,0 |
| 0 0 | -1,0 | 0,0 | 1,0 |
| 1 | 0,0 | 1,0 | -1,1 |
Três argumentos: somador completo
Ao contrário do semi-somador,
um somador
completo recebe três entradas A, B, Cin e calcula duas saídas S e Cout relacionadas como A + B + Cin = S + 3 * Cout.
Soma de três trits
Se queremos calcular uma soma de A + B + Cin, a idéia é a mesma de antes: usamos a preparação de entradas camada por camada. A primeira camada recebe A como entrada, a segunda usa B e a última camada de multiplexador único usa Cin. Aqui está uma maneira possível de calcular a saída S:
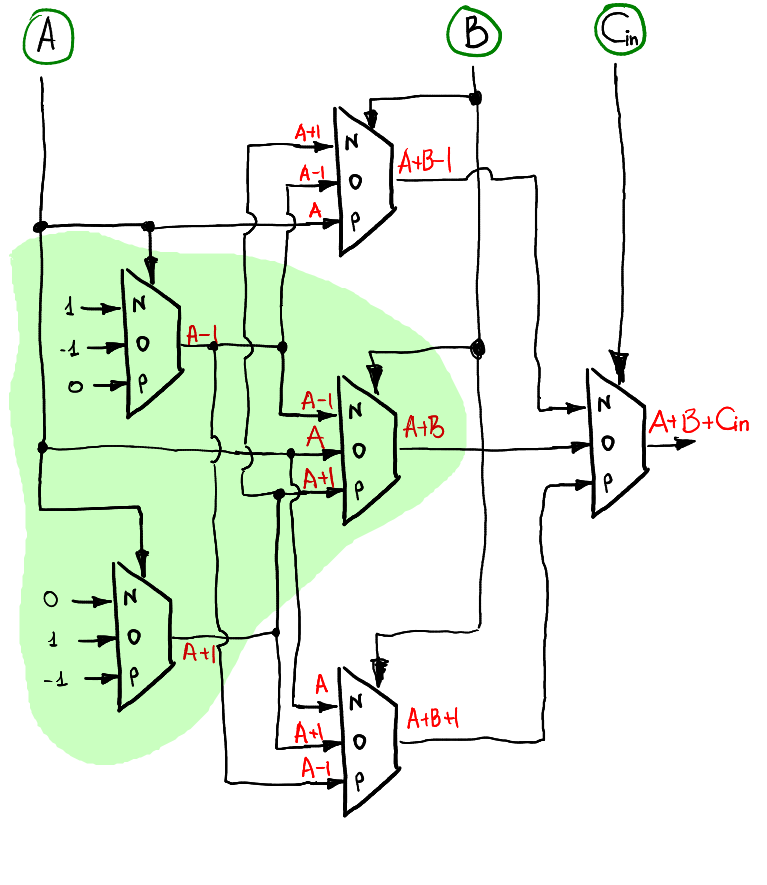
Observe que quando Cin = 0, ele se comporta exatamente da mesma maneira que o meio-adicionador, portanto, é natural ver a inclusão (destacada em verde) dos esquemas de meio-adicionador no adicionador completo.
Estouro (sinalizador de transporte)
O trit overflow pode ser calculado da mesma maneira camada por camada. Também inclui o meio adicionador!
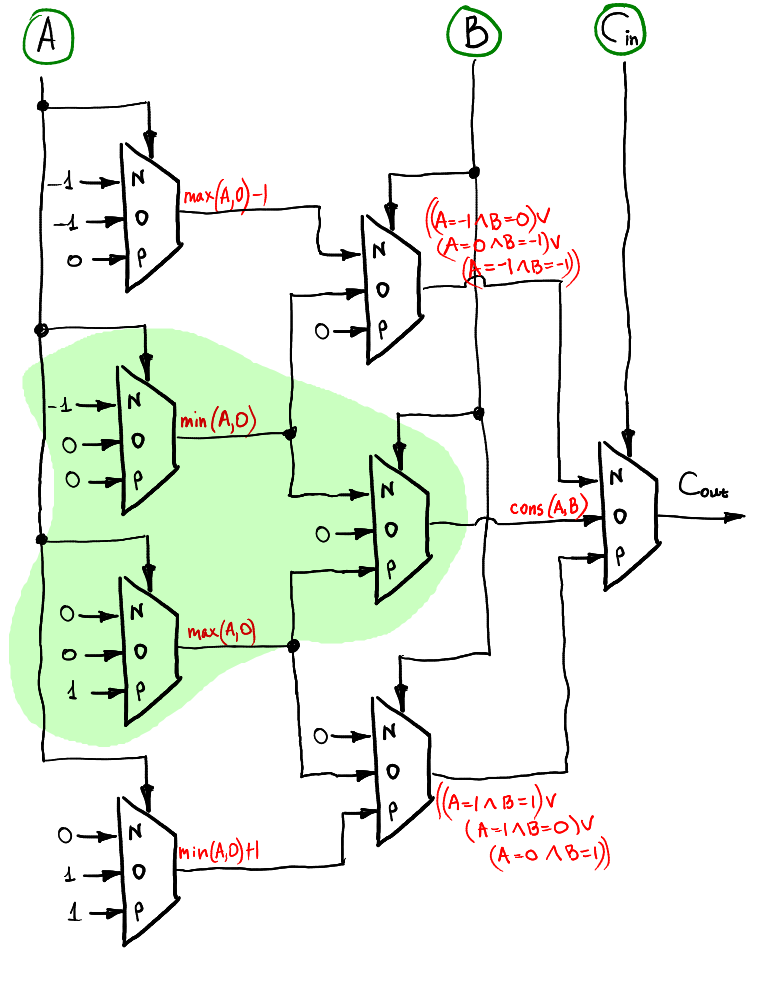
Validação de hardware
Dessa vez, fiquei com preguiça de usar as placas de ensaio para testar o somador total, então fiz esse PCB de uma camada:

Aqui está depois que o cobre foi gravado:

Três tabelas a seguir listam todos os 27 estados possíveis do somador completo. Como antes, as fotos estão disponíveis para cada estado. Observe que a tabela do meio (Cin = 0) é exatamente a mesma da metade da somador.
A vantagem do somador completo em relação ao meio-somador é a possibilidade de empilhar vários somadores até obtermos trits suficientes para representar o número que queremos.
Aqui está uma pilha de dois somadores:

E aqui como ele resolve -4 + 2 (o trit menos significativo está à esquerda):

Obviamente, não precisamos de um quadro de somador completo para o trit menos significativo (não temos uma bandeira de transporte para a entrada do trit menos significativo), o meio-somador seria suficiente.
Conclusão
Este é o fim da introdução à computação ternária. Fique atento a relógios, contadores, memória e muito mais!