🛌🏻 🥜 🚣🏿 Computação quântica em jogos ou enlouquecendo seriamente 👰🏾 👨‍👩‍👧 ⚪️

Se você mora entre os loucos, precisa aprender a ser louco

Você já tentou "aprender a ser louco"? Tarefa não trivial. Você nem encontra uma técnica normal, porque todo mundo enlouquece à sua maneira. Minha primeira tentativa: teoria da conspiração. A teoria não envolve prática, o que significa que você não precisa trabalhar duro. Novamente, em qualquer situação, ninguém sofrerá.

Como criar teorias da conspiração?

Criar uma teoria da conspiração é relativamente simples. Precisamos de uma idéia que seja simples o suficiente para ser aceita por 90% da população. Deve ser controverso, para que 5% da população possa explicar 90% de quais são os idiotas. Por fim, precisamos de algumas pesquisas que essas 95% das pessoas não entendem, mas que são usadas por 90% como argumento "as pessoas se mostraram mais inteligentes que nós ...".

A computação quântica é uma ótima área para esse estudo. Você pode criar um esquema simples, mas a palavra "quantum" adicionará peso aos resultados.

O objeto de estudo é um jogo, pois se deve à juventude simples e familiar. Quem está envolvido na computação quântica e nos jogos? Google

Então, teoria herética: depois de 5 anos, Page e Green decidirão quem será o principal no Google e farão isso com a ajuda do jogo. Cada um deles tem um grupo de pesquisadores. A equipe AlphaGo, com suas redes neurais de ~~combate~~ , puxou rivais em Go. Os opositores foram forçados a procurar novos métodos e ainda encontraram um instrumento de ~~total~~ superioridade: a computação quântica.

Posso usar a Quantum Computing para jogos? Fácil. Vamos mostrar, por exemplo, que o jogo "caçador de raposas" pode ser "resolvido" em 6 movimentos. Por uma questão de credibilidade, nos restringimos a 15 qubits (a quirk do editor on-line não emula por mais de quinze), por uma questão de simplicidade, ignoramos as limitações da arquitetura do processador e correção de erros.

As regras

Extremamente simples. Existem cinco orifícios dispostos em uma fila (nós os numeramos como 0-1-2-3-4). Em um deles é uma raposa. Toda noite, a raposa passa para a próxima marta, esquerda ou direita. Todas as manhãs, o caçador pode verificar um buraco para escolher. A tarefa do caçador é pegar a raposa. A tarefa da raposa é sobreviver. Em teoria, uma raposa pode fugir de um caçador para sempre. Na prática, existe uma estratégia vencedora: verifique os buracos 1-2-3-1-2-3. Somente essa estratégia vou testar.

Construindo um esquema

Vamos começar com o início dos qubits 0-1-2-3-4 (5 orifícios). Aqui você pode editar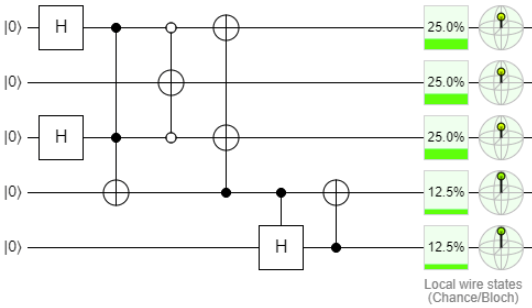

De fato, após a iniciação, temos um sistema no qual, após a medição, estritamente um qubit será único. As probabilidades de "unidade" diferem para cada qubit, mas no nosso caso isso não é crítico. Devemos deixar espaço para discussão sobre o esquema (e nossa teoria ao mesmo tempo).

No Q #, obtemos código como este:

operation TestStrategy () : (Result) { let res = Zero; using(qubits=Qubit[16]) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history InitFoxHoles(qubits); ResetAll(qubits); // ALWAYS clean after yourself } return Zero; } // Inits fox holes, with almost equal probabilities operation InitFoxHoles(register: Qubit[]) : Unit { body { ResetAll(register); // Step 1 H(register[0]); H(register[2]); // Step 2 (Controlled (X))([register[0],register[2]], register[3]); // Step 3 X(register[0]); X(register[2]); (Controlled (X))([register[0],register[2]], register[3]); X(register[0]); X(register[2]); // Step 4 CNOT(register[3], register[0]); CNOT(register[3], register[2]); // Step 5 (Controlled (H))([register[3]], register[4]); // Step 6 CNOT(register[4], register[3]); } }

O TestStrategy testará nossa estratégia 1-2-3-1-2-3, InitFoxHoles () é responsável apenas pelo início de buracos de raposa. Vamos verificar a iniciação. Copie o TestStrategy, inicie a iniciação, meça os 5 primeiros qubits e retorne seus valores.

  operation TestInit(): (Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; using(qubits=Qubit[16]) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history InitFoxHoles(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4); } }

Executaremos o teste mil vezes (várias execuções são típicas de algoritmos quânticos, em alguns locais até necessários). Código de chamada - no spoiler, resultados: na tela abaixo.

Teste rapidamente a iniciação

  static void TestInitiation() { using (var sim = new QuantumSimulator()) { var initedQubitsValues = Enumerable.Range(0, 5) .ToDictionary(qubitIndex => qubitIndex, oneMesaured => 0); for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result) result = TestInit.Run(sim).Result; if (result.Item1 == Result.One) { initedQubitsValues[0]++; } if (result.Item2 == Result.One) { initedQubitsValues[1]++; } if (result.Item3 == Result.One) { initedQubitsValues[2]++; } if (result.Item4 == Result.One) { initedQubitsValues[3]++; } if (result.Item5 == Result.One) { initedQubitsValues[4]++; } } Console.WriteLine($"Qubit-0 initiations: {initedQubitsValues[0]}"); Console.WriteLine($"Qubit-1 initiations: {initedQubitsValues[1]}"); Console.WriteLine($"Qubit-2 initiations: {initedQubitsValues[2]}"); Console.WriteLine($"Qubit-3 initiations: {initedQubitsValues[3]}"); Console.WriteLine($"Qubit-4 initiations: {initedQubitsValues[4]}"); } }

Algo deu errado. Uma distribuição quase uniforme era esperada. O motivo é simples: no passo 3, inverti o terceiro qubit, em vez do primeiro: (Controlado (X)) ([registrador [0], registrador [2]], registrador [3]); ~~não é~~ bom copiar e colar velho.

Nós corrigimos o código, executamos o teste:

Iniciação corrigida

  // Inits fox holes, with almost equal probabilities operation InitFoxHoles(register: Qubit[]) : Unit { body { ResetAll(register); // Step 1 H(register[0]); H(register[2]); // Step 2 (Controlled (X))([register[0],register[2]], register[3]); // Step 3 X(register[0]); X(register[2]); (Controlled (X))([register[0],register[2]], register[1]); X(register[0]); X(register[2]); // Step 4 CNOT(register[3], register[0]); CNOT(register[3], register[2]); // Step 5 (Controlled (H))([register[3]], register[4]); // Step 6 CNOT(register[4], register[3]); } } }

Já está melhor. O código pode ser visto no nabo, versão Commit 1 .

Onde correr a raposa?

Selecione o qubit qubit (a numeração começa de cima) sob a direção atual da raposa. Concordamos que zero significa movimento descendente, uma unidade significa movimento ascendente. Obviamente, se a raposa já estiver no buraco zero - ela deve descer. Se a raposa estiver no quarto buraco, ela se move para cima. Em outros casos, a raposa pode se mover para cima e para baixo. De acordo com essas regras simples, podemos definir o “qubit da direção atual” para 0, 1 ou uma superposição de zero e um. Examinamos o código no repositório, Commit 2 .

Esquema no editor.

Código e teste

 // Select next Fox movement direction, updating qubit 5 // 1 means go up (4 -> 3, 3 -> 2, ... 1 -> 0) // 0 means go down (0 -> 1, 1 -> 2, ... 3 -> 4) operation SetupMovementDirection(qubits: Qubit[]) : Unit { body { // Step 1 CNOT(qubits[4], qubits[5]); // Step 2 (Controlled (H))([qubits[3]], qubits[5]); // Step 3 (Controlled (H))([qubits[2]], qubits[5]); // Step 4 (Controlled (H))([qubits[1]], qubits[5]); } } operation TestMovementDirectionSetup(): (Result, Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; mutable res5 = Zero; using(qubits=Qubit[16]) { InitFoxHoles(qubits); SetupMovementDirection(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); set res5 = M(qubits[5]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4, res5); } }

  static void TestMovementDirectionSetup() { using (var sim = new QuantumSimulator()) { List<string> results = new List<string>(); string initedCubit = null; string moveDirection = null; for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result, Result) result = Quantum.FoxHunter.TestMovementDirectionSetup.Run(sim).Result; if (result.Item1 == Result.One) { initedCubit = "0"; } if (result.Item2 == Result.One) { initedCubit = "1"; } if (result.Item3 == Result.One) { initedCubit = "2"; } if (result.Item4 == Result.One) { initedCubit = "3"; } if (result.Item5 == Result.One) { initedCubit = "4"; } if (result.Item6 == Result.One) { moveDirection = "1"; } else { moveDirection = "0"; } results.Add($"{initedCubit}{moveDirection}"); } foreach(var group in results .GroupBy(result => result) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} was measured {group.Count()} times"); } Console.WriteLine($"\r\nTotal measures: {results.Count()}"); } }

Movimento

Implementado por SWAP controlado. Se o qubit de controle for único - troque para baixo. Se o qubit de controle for zero, trocamos.

Esquema no editor .

Operador Q #

  // Makes a movement based on the 5'th qubit value // 1 means go up (4 -> 3, 3 -> 2, ... 1 -> 0) // 0 means go down (0 -> 1, 1 -> 2, ... 3 -> 4) operation MakeMovement(qubits: Qubit[]) : Unit { body { // Code movement Up // Step 1 mutable qubitsToSwap = [qubits[0], qubits[1]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 2 set qubitsToSwap = [qubits[1], qubits[2]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 3 set qubitsToSwap = [qubits[2], qubits[3]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 4 set qubitsToSwap = [qubits[3], qubits[4]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // COde movement down X(qubits[5]); // Invert direction qubit for the ZeroControlled operations // Step 5 set qubitsToSwap = [qubits[3], qubits[4]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 6 set qubitsToSwap = [qubits[2], qubits[3]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 7 set qubitsToSwap = [qubits[1], qubits[2]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 8 set qubitsToSwap = [qubits[0], qubits[1]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); X(qubits[5]); // Back-invert for the direction qubit } }

Q #: declaração para testes

  operation TestFirstMovement(): (Result, Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; mutable res5 = Zero; using(qubits=Qubit[16]) { InitFoxHoles(qubits); SetupMovementDirection(qubits); MakeMovement(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); set res5 = M(qubits[5]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4, res5); } }

Código c #

  static void TestFirstMove() { using (var sim = new QuantumSimulator()) { List<string> results = new List<string>(); string initedCubit = null; string moveDirection = null; for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result, Result) result = Quantum.FoxHunter.TestFirstMovement.Run(sim).Result; if (result.Item1 == Result.One) { initedCubit = "0"; } if (result.Item2 == Result.One) { initedCubit = "1"; } if (result.Item3 == Result.One) { initedCubit = "2"; } if (result.Item4 == Result.One) { initedCubit = "3"; } if (result.Item5 == Result.One) { initedCubit = "4"; } if (result.Item6 == Result.One) { moveDirection = "1"; } else { moveDirection = "0"; } results.Add($"{initedCubit}{moveDirection}"); } // Holes measurements foreach (var group in results .GroupBy(result => result[0]) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} hole was measured {group.Count()} times"); } // Directions measuremetns foreach (var group in results .GroupBy(result => result[1]) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} direction was measured {group.Count()} times"); } Console.WriteLine($"\r\nTotal measures: {results.Count()}"); } }

O código pode ser exibido no Commit 3 .

Nós fazemos 6 movimentos

Finalmente, selecionamos o sexto qubit para o status do jogo (a raposa é livre / a raposa não é livre). A unidade corresponde a uma raposa livre. Nós faremos outros movimentos apenas com um único qubit de status.

Os qubits 7,8,9,10,11 manterão um histórico de jogadas. Após cada movimento, vamos trocar um deles com um qubit da direção atual (isso nos permitirá armazenar o histórico de movimentos e redefinir o qubit da direção atual antes de cada movimento).

Esquema em anexo .

Operador Q #

  /// Make 6 movements. Every movement is controlled by the 6'th qubit. /// After the every qubit we check if the fox has been captured and invert the 6'th qubit /// Reminder: 6'th qubit equal to One means "Fox is free, go further" operation MakeSixMovements(qubits: Qubit[]) : Unit { body { // Move 1 (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Reverse Fox State if it's shot // Move 2 SwapReverseRegister([qubits[5], qubits[7]]); // Move the first move direction to the qubit 7, qubit 5 is Zero again (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 3 SwapReverseRegister([qubits[5], qubits[8]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); // Move 4 SwapReverseRegister([qubits[5], qubits[9]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Move 5 SwapReverseRegister([qubits[5], qubits[10]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 6 SwapReverseRegister([qubits[5], qubits[11]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); } }

Q #: declaração para testes

  operation TestSixMovements(): (Result) { body { mutable res = Zero; using(qubits=Qubit[16]) { ResetAll(qubits); InitFoxHoles(qubits); X(qubits[6]); // At the beginning of the game our fox is alive MakeSixMovements(qubits); set res = M(qubits[6]); ResetAll(qubits); // ALWAYS clean after yourself } return (res); } }

C #: teste

  static void TestMovements() { using (var sim = new QuantumSimulator()) { int zerosCount = 0; for (int i = 0; i < 1000; i++) { Result result = Quantum.FoxHunter.TestSixMovements.Run(sim).Result; if(result == Result.Zero) { zerosCount++; } } Console.WriteLine($"\r\nTotal zeroes: {zerosCount}"); } }

Observamos o Commit 4 .

Toques finais

Temos um erro no circuito. Como testamos a estratégia 1-2-3-1-2-3, verificamos cada buraco duas vezes. Assim, tendo capturado a raposa no primeiro movimento, passaremos pelo qubit de status duas vezes (no primeiro e no quarto).

Para evitar essa situação, usamos 12 qubits para corrigir o status após os movimentos 4-5-6. Além disso, adicionamos a definição de vitória: se pelo menos um dos qubits de status virar zero, vencemos.

O esquema final .

Q #: corrija o operador 6 move

  operation MakeSixMovements(qubits: Qubit[]) : Unit { body { // Move 1 (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Reverse Fox State if it's shot // Move 2 SwapReverseRegister([qubits[5], qubits[7]]); // Move the first move direction to the qubit 7, qubit 5 is Zero again (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 3 SwapReverseRegister([qubits[5], qubits[8]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); // Move 4 SwapReverseRegister([qubits[5], qubits[9]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[1], qubits[12]); // Move 5 SwapReverseRegister([qubits[5], qubits[10]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[2], qubits[12]); // Move 6 SwapReverseRegister([qubits[5], qubits[11]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[3], qubits[12]); } }

P #: corrija a estratégia de teste do operador 1-2-3-1-2-3

  operation TestStrategy () : (Result) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history // 12 - another qubit of the fox live. 1 means "fox is still free, go further" // 13 Result qubit. If it's zero, the fox is alive body { mutable res = Zero; using(qubits=Qubit[14]) { ResetAll(qubits); // Init fox positions and the fox' live InitFoxHoles(qubits); X(qubits[6]); // At the beginning of the game our fox is alive X(qubits[12]); // The second qubit of the fox live. If it's one - the fox is alive. // Make moves MakeSixMovements(qubits); // Measure results. If the 13'th qubit is zero the fox is alive X(qubits[6]); X(qubits[12]); CNOT(qubits[6], qubits[13]); CNOT(qubits[12], qubits[13]); CCNOT(qubits[6], qubits[12], qubits[13]); set res = M(qubits[13]); ResetAll(qubits); // ALWAYS clean after yourself } return (res); } }

C #: executar verificação final

  static void RunFoxHunt() { Stopwatch sw = new Stopwatch(); sw.Start(); using (var sim = new QuantumSimulator()) { var foxSurvives = 0; var hunterWins = 0; for (int i = 0; i < 1000; i++) { var result = (Result)(TestStrategy.Run(sim).Result); if (result == Result.Zero) { foxSurvives++; } else { hunterWins++; } } Console.WriteLine($"Fox survives: \t{foxSurvives}"); Console.WriteLine($"Hunter wins: \t{hunterWins}"); } sw.Stop(); Console.WriteLine($"Experiment finished. " + $"Time spent: {sw.ElapsedMilliseconds / 1000} seconds"); }

Confirme 5 .

O que se segue

Em princípio, o esquema pode ser otimizado tanto no número de qubits quanto no número de operações. A otimização trivial para o número de qubits é livrar-se do qubit-13, retornando apenas 6 e 12. Otimização para operações - para dar o primeiro tiro imediatamente após o início. No entanto, vamos deixar esse trabalho para os engenheiros do Google.

Como você pode ver, qualquer pessoa que esteja familiarizada superficialmente com a computação quântica pode interpretar com segurança o "caçador de raposas". Se tivéssemos um pouco mais de qubits, poderíamos encontrar a solução ideal e não verificar a existente. É inteiramente possível que o jogo da velha (e sua versão quântica), damas, xadrez, Go caiam a seguir.

Ao mesmo tempo, a questão da "solvabilidade" de jogos como DotA, Starcraft e Doom permanece em aberto. Para a computação quântica, o armazenamento de todo o histórico de cliques é característico. Tomamos APM (Ações por minuto) de 500, multiplicamos pelo número de jogadores, multiplicamos pelo número de minutos, adicionamos a aleatoriedade do jogo em si - o número de qubits necessários para armazenar todas as informações cresce muito rapidamente.

Portanto, escolher um jogo em uma pequena competição entre Brin e Page pode desempenhar um papel decisivo. No entanto, a geração de um jogo "igualmente difícil" para computadores clássicos e quânticos merece sua própria teoria.

Computação quântica em jogos ou enlouquecendo seriamente