Que devemos construir uma estrada. Parte 1

O itinerário diário da maioria de nós se limita a viajar de casa para o trabalho e voltar. E o obstáculo mais difícil que pode retardar nosso movimento são os engarrafamentos. Mas em nosso país, há um grande número de lugares onde você só pode entrar em veículos especiais.

Esse transporte é bom se você não precisar transportar grandes volumes de carga ou viajar para áreas inacessíveis regularmente. Então, já devemos pensar em construir infraestrutura, cujo movimento é possível no transporte civil usual.

E é bom que toda a complexidade do projeto de uma rota futura seja encontrar uma régua e um lápis para desenhar uma linha reta no mapa, conectando alguns objetos. Mas, infelizmente, a nossa realidade é muito diferente disso. E se o terreno voando acima dele se assemelhar a um bom pedaço de queijo suíço?

Por mais de um ano, trabalhamos com colegas do laboratório de pesquisa de Design Digital para criar uma ferramenta que pode construir várias redes de comunicação no modo automático. Para detalhes, bem-vindo ao gato.

Como tudo começou

Normalmente, as viagens para esses lugares remotos são devidas a certos benefícios financeiros. E, embora muitas vezes se saiba com antecedência que o desenvolvimento dessas áreas trará bons lucros, por que não economizar dinheiro com coisas que podem ser feitas sem dificuldades especiais? E se uma rota projetada com mais competência nos permitir não construir vários quilômetros extras da rodovia?

Mas apenas a disponibilidade de estradas para obter lucro significativo claramente não é suficiente. E basicamente é trazido apenas por depósitos minerais. Portanto, além das estradas, é necessário projetar uma rede de vários dutos, uma rede de dutos, uma rede de linhas de energia com subestações elétricas corretamente posicionadas. Toda essa infraestrutura pode ser designada como objetos lineares.

E quando um engenheiro é confrontado com a tarefa de projetar uma rede de comunicações no terreno com condições geológicas e de engenharia complexas, uma tarefa analítica incrivelmente complexa recai sobre ele.

Como não entrar na zona de inundação do rio? Como minimizar o caminho em solos permafrost? Como economizar na quantidade de almofada de areia ao atravessar um pântano? Onde conseguir areia para este travesseiro?

Essa é apenas uma pequena fração das perguntas que um engenheiro faz a si mesmo durante o trabalho e, no entanto, você ainda precisa levar em consideração vários GOSTs e SNiPs. E bem, se você deseja conectar apenas dois objetos, e se houver algumas dúzias de objetos?

Portanto, a indústria de design precisa urgentemente de uma ferramenta que possa calcular o custo de objetos lineares projetados por um engenheiro e a capacidade de construí-los no modo automático.

Dados

A primeira coisa que tivemos que lidar quando iniciamos a tarefa foi a pesquisa de dados. Quais dados são necessários? Onde consegui-los? E se a segunda pergunta puder ser resolvida com a ajuda do usuário, para entender a primeira pergunta, precisamos de análises sérias.

E os dados para o cálculo correto exigem realmente muito - a partir da marcação mais banal da área em que lagos e rios estão marcados, vários pântanos e áreas cársticas, nas quais é altamente recomendável não construir por causa da ameaça de colapso. Portanto, além das áreas que podem ser vistas a partir do satélite, os dados dos estudos geológicos da área também são necessários aqui.

Mas nem todos os dados são limitados a objetos naturais em nosso país. Há também um monte de coisas que foram criadas pelo homem. Por exemplo, no caso de construção de estradas, podemos usar as estradas que foram construídas anteriormente. Mas na construção de dutos, o uso da infraestrutura existente está longe de ser sempre possível. Como a conexão de um novo gasoduto a uma rede existente pode não passar no cálculo hidráulico.

Além da reutilização do que foi criado anteriormente pelo homem, também é preciso levar em consideração várias restrições à construção perto de qualquer objeto. Por exemplo, para a construção de linhas de energia, é necessário levar em consideração os recuos dos locais de habitação humana, dependendo da tensão na própria linha de energia.

Mas não é inteiramente correto considerar o cálculo do problema apenas em um plano, pois além do terreno plano, existem áreas com uma grande diferença de altitude, nas quais a construção também não pode ser realizada.

A obtenção de dados no terreno é um processo muito mais simples do que os dados sobre a marcação de áreas e a infraestrutura existente. Para simplificar o desenvolvimento, usamos dados abertos de elevação SRTM (Shuttle Radar Topography Mission) que qualquer pessoa pode obter.

Então, nós temos os dados, sabemos onde podemos construir, onde não podemos construir, existem custos de construção para diferentes áreas do terreno. Temos uma região, tem um conjunto de objetos que queremos conectar em uma única rede de comunicação. Em termos matemáticos, isso soará como uma busca por uma solução para o problema de Steiner.

Um pouco de matemática

Sabe-se que cada fórmula reduz pela metade o número de leitores, por isso reduzimos drasticamente esta seção ...

Para otimizar a rota da instalação linear projetada, é necessário poder calcular seu custo de construção. Cada objeto linear pode ser representado como uma polilinha $$$L = \ {A_i, B_i \} _ {i = 0} ^ n$ constituído por segmentos $$$AB_ {i}$ .
O custo de construção de cada seção reta pode ser representado como um valor da função $$$C_ {AB_ {i}}$ , em que cada segmento é especificado parametricamente:

$$$$ display $$ {\ displaystyle AB_i \ colon \ left \ {{\ begin {alinhado} & s = s \ esquerda (t \ direita) - \ mbox {curva parametrizada}, \\ & h = h \ left (s (t ) \ right) - \ mbox {função da altura da elevação}, \\ & c = c \ left (s (t) \ right) - \ mbox {função do custo unitário da construção em um ponto}, \\ \ end {align}} \ right .} $$ exibir $$

onde $$$t \ in \ left [0, 1 \ right]$ - parametrização de segmento.

$$$C_ {AB_i} = \ int \ limits_ {AB_i} c \ left (s (t) \ right) \ sqrt {\ left [g_ {xy} (s (t)) + \ frac {\ h parcial] {\ s_x parcial} \ cdot \ frac {\ parcial h} {\ parcial s_y} \ direita] \ ponto {s} _ {x} \ ponto {s} _ {y}} dt$ onde $$$g$ - o tensor métrico da superfície da Terra sem levar em consideração o relevo, ou seja, em palavras simples, a função de medir a distância na superfície da Terra.

Devido ao fato de nosso planeta ter a forma de um geóide, é necessário usar fórmulas especiais para medir distâncias. Para isso, usamos a fórmula Haversinus. Nele, a forma do planeta se parece com uma esfera, mas isso é suficiente para nossos propósitos, pois o erro de medição é de cerca de 0,3% e a velocidade de cálculo das distâncias por esse método permanece alta.

Abordagens para encontrar o melhor caminho

Porém, antes de ingressar em um grupo de objetos, você precisa aprender a encontrar o caminho ideal entre os dois. Duas maneiras de fazer isso imediatamente vêm à mente:

1. crie um gráfico e aplique os métodos de pesquisa de caminho mais curto;
2. use uma solução baseada em métodos de otimização.

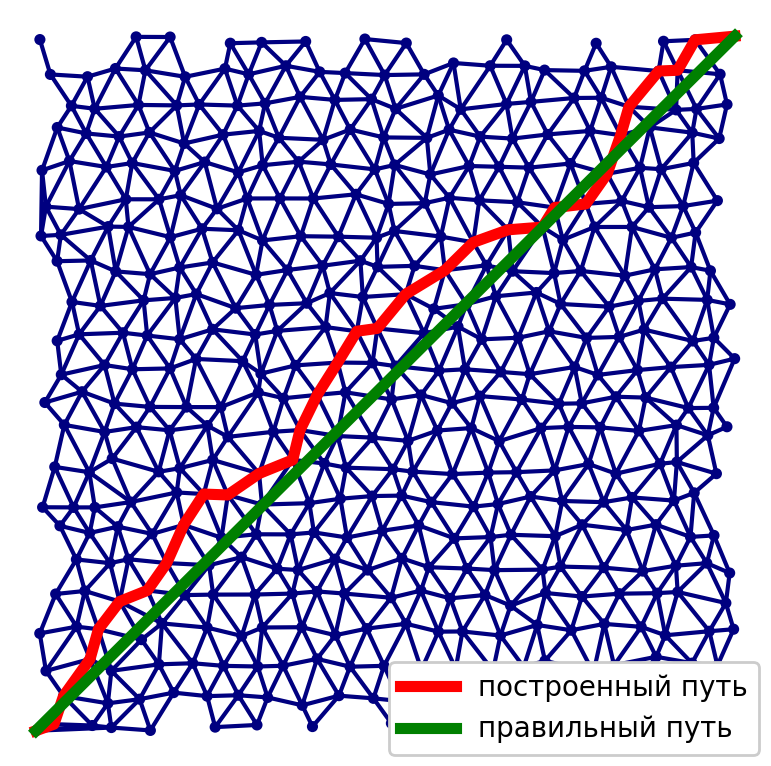
Ao implementar o primeiro método, temos um problema associado ao método de construção de um gráfico para obter a maior precisão possível da solução. É necessário encontrar um equilíbrio entre o número de vértices e arestas no gráfico, a qualidade da solução e o tempo necessário para calculá-la.

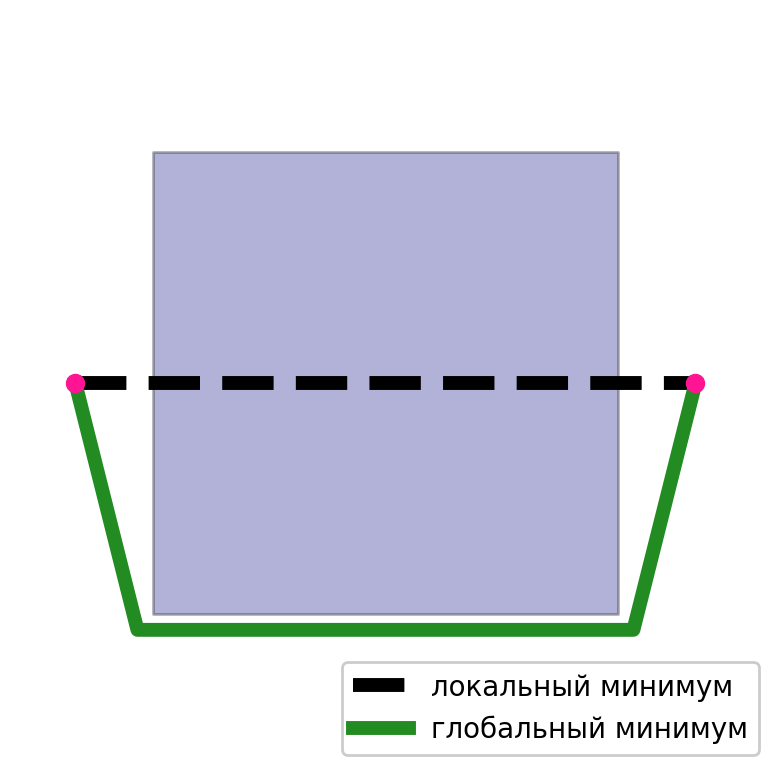
No segundo caso, o principal problema são os mínimos locais. É fácil escolher um caso em que a solução possa não convergir ou ficar longe do ideal. Como a solução obtida por esse método é incrivelmente dependente da aproximação inicial. Se tivermos uma boa aproximação inicial, o resultado será de alta qualidade.

Portanto, temos duas abordagens para resolver esse problema. O primeiro tem uma qualidade bastante baixa, mas não há problema de mínimos locais. O segundo tem um problema de mínimos locais, mas uma solução de alta qualidade. E se você combinar corretamente essas duas abordagens, as deficiências de cada uma desaparecerão. Tomamos a solução obtida no gráfico como uma aproximação inicial e aplicamos métodos de otimização a ela.

Nesta parte do artigo, consideraremos exatamente a solução proposta para esse problema no gráfico.

Seleção de ferramenta

Um plano de ação foi delineado, resta apenas "codificá-lo". Como no estágio inicial de redação do aplicativo, tínhamos pouco conhecimento sobre a área de assunto, precisávamos de uma linguagem flexível para que, no caso de alguns erros de cálculo arquiteturais, reescrevéssemos o código inteiro para algumas latas de cerveja à noite. Opcionalmente, eu também queria bibliotecas para todas as ocasiões, para não recorrer à invenção de bicicletas. Portanto, o Python foi escolhido como a principal linguagem de programação.

No aplicativo, usamos uma impressionante pilha tecnológica, que não se limita ao seguinte:

• bem torneado para trabalhar com dados geométricos como polígonos e polilinhas;
• geopandas para trabalhos convenientes com formas ;
• scipy para armazenar o gráfico calculado e encontrar o caminho mais curto, além de encontrar as árvores abrangentes mínimas;
• PyTorch por trabalhar com a função de custo;
• travesseiro para trabalhar com imagens.

Implementação

O módulo pode ser dividido em várias etapas:

• geração de função de custo;
• geração de grade computacional;
• construindo um gráfico baseado em uma grade;
• ponderação gráfica;
• cálculo dos caminhos mais curtos em um gráfico.

Como as arestas do gráfico são segmentos, podemos ponderar essas arestas calculando o valor de uma determinada integral, que é apresentada acima. Porém, existem muitas arestas no gráfico e, portanto, os valores de custos e alturas precisarão ser obtidos para um número muito grande de pontos, o que pode levar muito tempo.

Inicialmente, a idéia era encontrar o custo unitário da construção, determinando se um ponto pertence a um polígono. Mas essa idéia foi observada devido à alta complexidade algorítmica dessa abordagem, pois pode haver muitos polígonos, e cada um deles possui um grande número de vértices.

Portanto, para resolver esse problema, podemos representar todos os polígonos que temos na forma de uma imagem, que na forma matemática é uma matriz. Assim, podemos obter o custo unitário da construção em um ponto além de O (1) e, portanto, podemos obter o custo de construir uma nervura específica com alta precisão.

Agora estamos prontos para criar um gráfico, mas não há uma maneira única e correta de construí-lo para obter soluções de alta precisão. Para construir um gráfico, é necessário gerar uma grade computacional, a saber, um conjunto de pontos na região em questão, conectados na ordem correspondente por segmentos que formam as faces das células. As grades podem ser divididas em dois tipos: uniforme e desigual.

O modelo de grade uniforme descreve as coordenadas de pontos individuais, para que a distância entre os nós da grade seja a mesma. Uma grade irregular aparece como um conjunto aleatório de pontos individuais.

O uso de uma grade uniforme nem sempre gera um resultado de alta qualidade para a localização do caminho mais curto; portanto, é necessário testar essa abordagem em uma grade irregular. A mais versátil é a malha triangular.

A grade foi gerada através da introdução de ruído com um certo coeficiente em uma grade retangular uniforme e, em seguida, aplicando pontos de triangulação de Delaunay para esse conjunto de pontos.

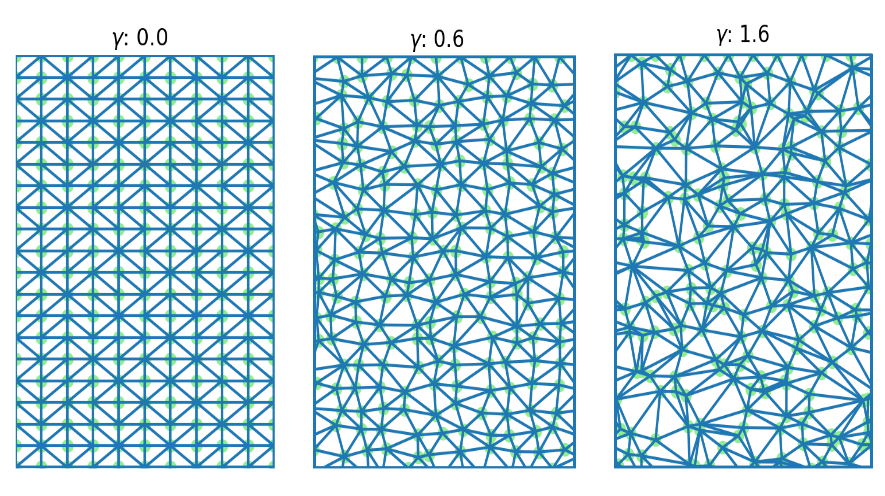
A eficácia das grades construídas foi testada em vários mapas modelo da área, que levaram em consideração os diferentes custos das regiões e o relevo e, em seguida, foi feita uma comparação com a solução obtida analiticamente. Ao pesquisar o comprimento da aresta do gráfico e o coeficiente de introdução de ruído na grade uniforme, foram encontrados parâmetros ideais para construir o caminho ideal entre dois pontos.

Questões principais

No início, tudo correu bem, o algoritmo calculou as redes ideais, mas uma vez houve um problema com a qualidade do caminho construído. O caso era bastante simples: você tinha que conectar dois objetos em um mapa bastante longo. O algoritmo não queria construir uma rota que estivesse obviamente correta.

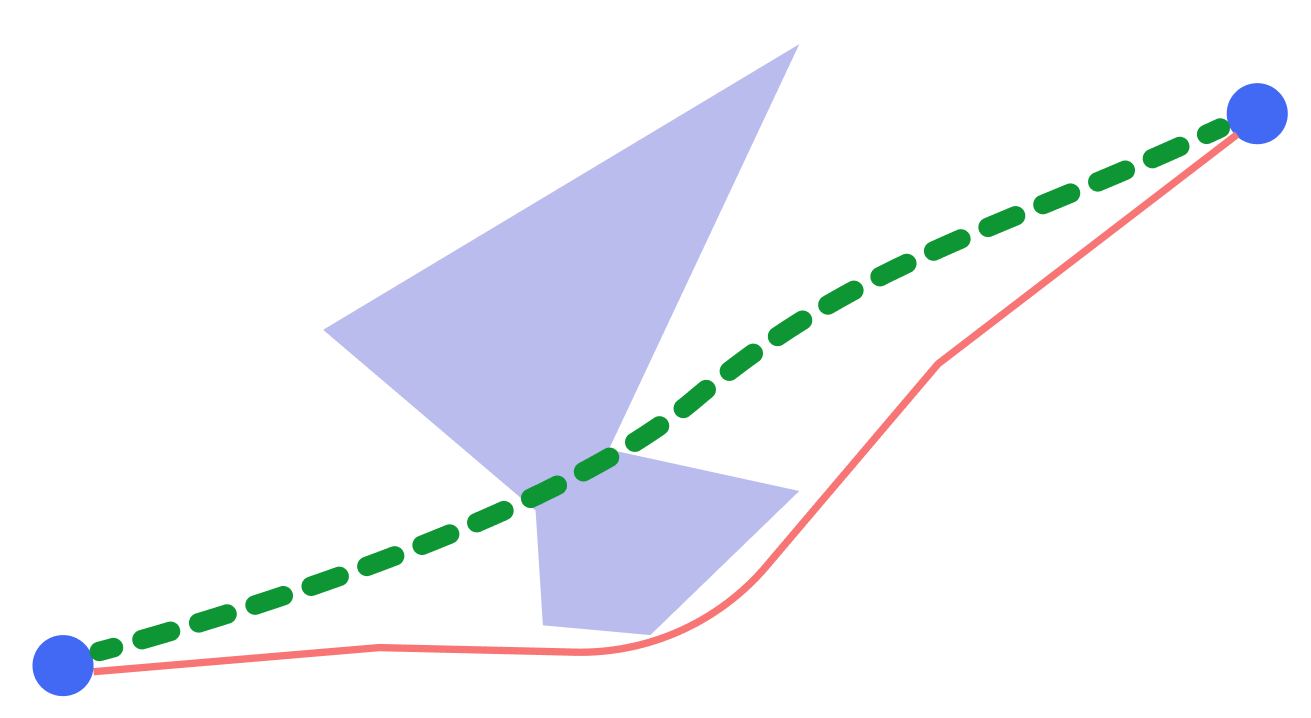
O problema, como sempre, estava com a grade computacional. Continuamos nossos experimentos com a aparência das grades e chegamos à conclusão de que conectar os vértices a um gráfico, em que cada vértice está conectado aos n vizinhos mais próximos, é a solução para nossos problemas.

Trabalho em rede

Depois que aprendemos a encontrar caminhos ótimos entre dois pontos, o próximo passo foi resolver o problema de construir uma rede ideal de objetos lineares. Os algoritmos encontrados na literatura para a construção de árvores Steiner em gráficos são orientados para problemas mais gerais e, portanto, serão ineficazes no nosso caso. Nosso gráfico é muito esparso, com um pequeno número de vértices terminais, em relação ao número total de vértices no gráfico, e nossa tarefa também é aplicada. Portanto, por várias outras razões, foi decidido desenvolver nosso próprio algoritmo que usa uma certa heurística para criar efetivamente uma rede ideal.

A descrição do algoritmo para construir a rede ideal no gráfico para o nosso caso é um tópico para uma publicação separada. Não vamos considerá-lo aqui. Como ao calcular uma tarefa real, é necessário levar em consideração muitas condições adicionais da indústria da construção que são relevantes para o usuário final, que impõem certas restrições ao algoritmo usado.

Caso real

Então, agora nos voltamos para os resultados do algoritmo. Nossa tarefa é conectar um determinado conjunto de objetos a uma rede de comunicação. A comparação dos resultados do algoritmo ocorreu com uma rede viária construída anteriormente. O comprimento total da rede existente é 153,5 km versus 122,6 km para a rede calculada. Isso proporciona uma redução de cerca de 25% no comprimento da rede rodoviária, o que, em última análise, economizará de 5 a 15% nos custos de construção de capital.

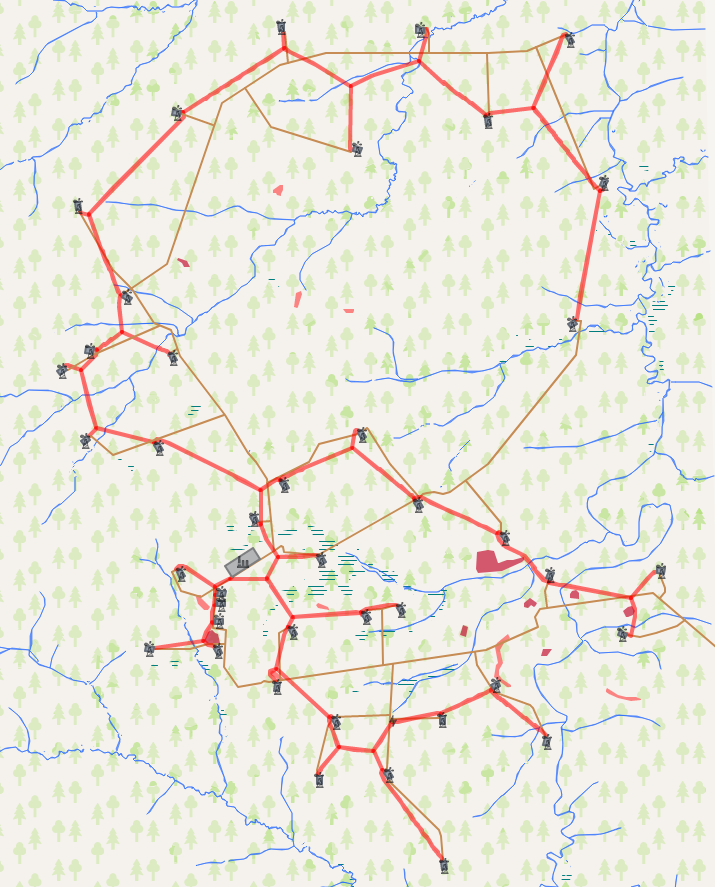
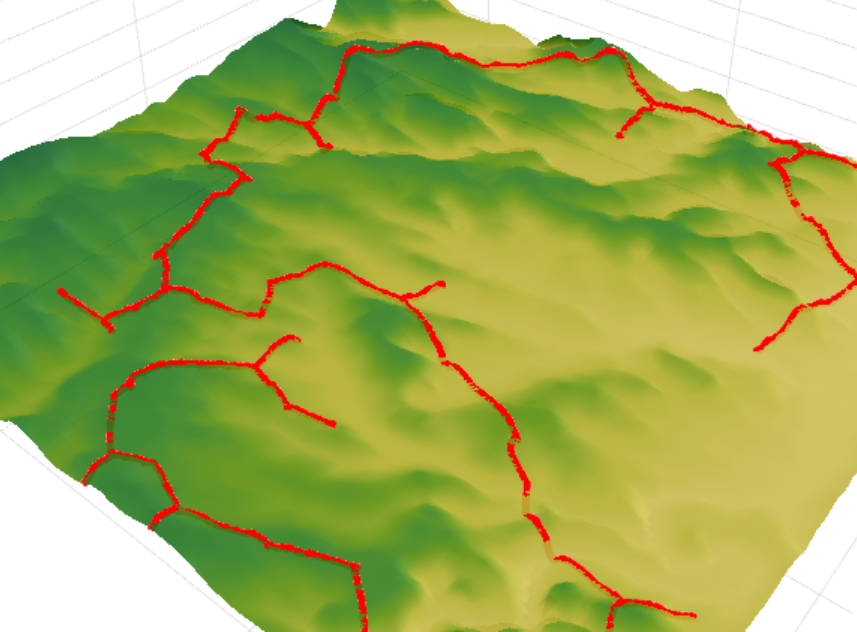
Você pode olhar mais de perto os resultados do cálculo aqui .

Uma descrição dos métodos de otimização usados ​​estará na próxima parte do artigo.