Os princípios matemáticos do layout automático

Muitos desenvolvedores acreditam que o Auto Layout é um freio e um problema, e é extremamente difícil depurá-lo. E é bom que essa conclusão seja feita com base em minha própria experiência e, às vezes, é apenas "eu ouvi dizer que nem vou tentar fazer amizade com ele".

Mas talvez o motivo não esteja fora, mas dentro. Por exemplo, os pássaros mais perigosos do mundo da casuar não atacarão as pessoas sem motivo, apenas por autodefesa. Portanto, tente assumir por um segundo que isso não é ruim para o Auto Layout, e você não o entende bem o suficiente e não sabe cozinhar. Foi isso que Anton Sergeyev fez e se aprofundou na teoria para entender tudo exatamente. Nos é oferecido um aperto pronto sobre os fundamentos matemáticos do Auto Layout.




Auto Layout é um sistema de layout . Antes de investigarmos, vamos falar sobre tipografia moderna em geral. Então, vamos lidar com o Auto Layout - vamos descobrir qual tarefa ele resolve e como o faz. Vamos considerar os recursos na implementação do Layout automático no iOS e tentar desenvolver dicas práticas que podem ajudar no trabalho com ele.

Como a história será muito próxima de um artigo matemático, concordamos primeiro com a notação para falar o mesmo idioma.


Sobre o palestrante: Anton Sergeev ( antonsergeev88 ) trabalha na equipe Yandex.Mart, lida com o cliente móvel do Maps no iOS. Antes do desenvolvimento móvel, ele lidava com sistemas de controle de usinas de energia, onde o custo dos erros no código é alto demais para ser tolerado.

Designações

Os sistemas de equações lineares são familiares para nós desde a escola - eles são indicados por um colchete e sua solução já está ausente. Além disso, sistemas de equações lineares possuem entidades que operam com restrições de layout automático. Eles são indicados por uma linha reta.



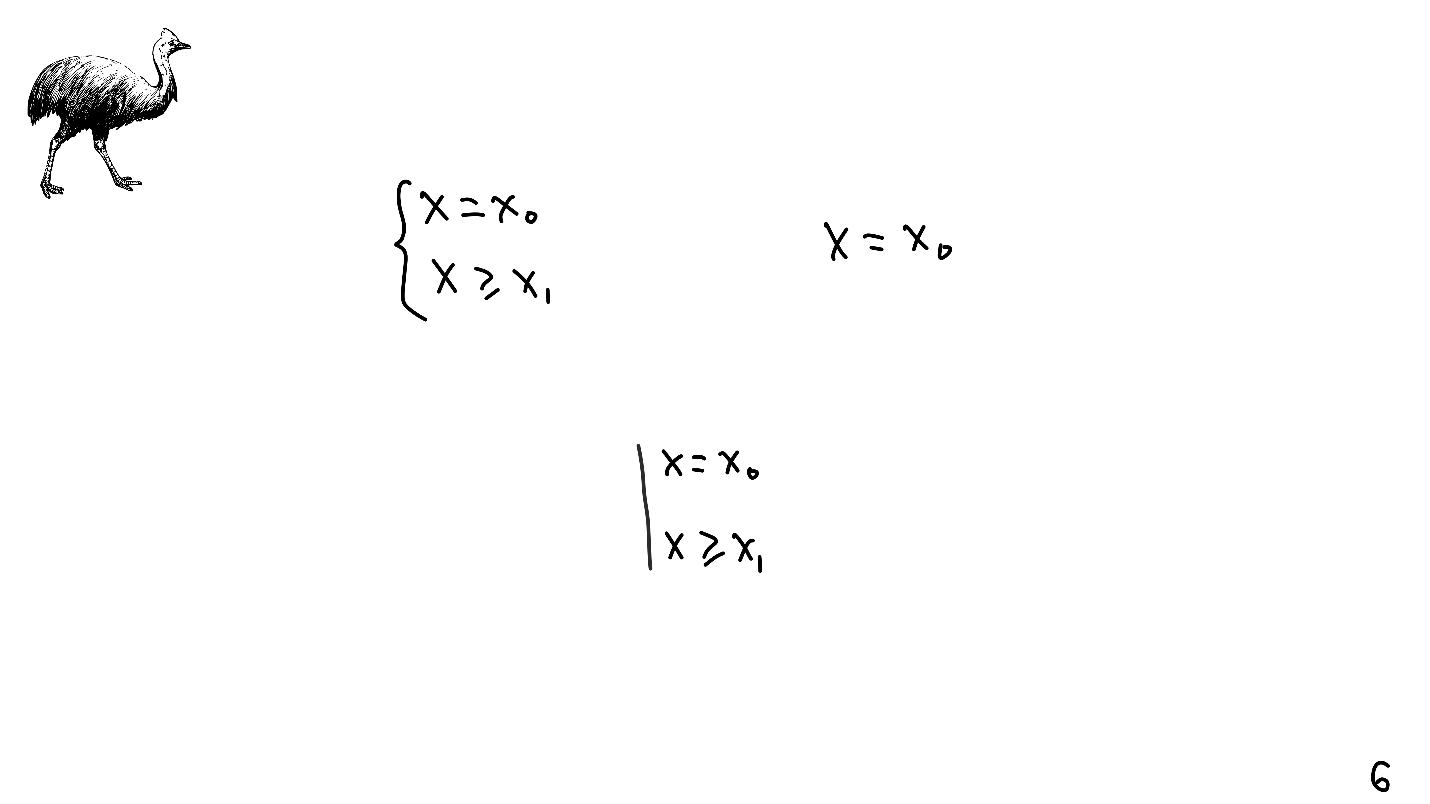
O pássaro estranho e, como já sabemos, perigoso não é acidentalmente pintado no canto superior do slide. Em homenagem ao cassowary (lat. Cassowary), que, é claro, mora na Austrália, um algoritmo é nomeado em todos os nossos iPhones.

O layout automático tem suas próprias limitações; as cores serão definidas em ordem de prioridade: vermelho - obrigatório; amarelo - alto; azul - baixo.

Layout

Quando eu estava preparando a apresentação, coloquei vários elementos na tela, por exemplo, um casuar. Para fazer isso, determinei que o casuar é uma figura retangular. Você precisa organizá-lo em uma folha que tenha eixos e seu próprio sistema de coordenadas, e para isso eu determinei as coordenadas do canto superior esquerdo, largura e altura.



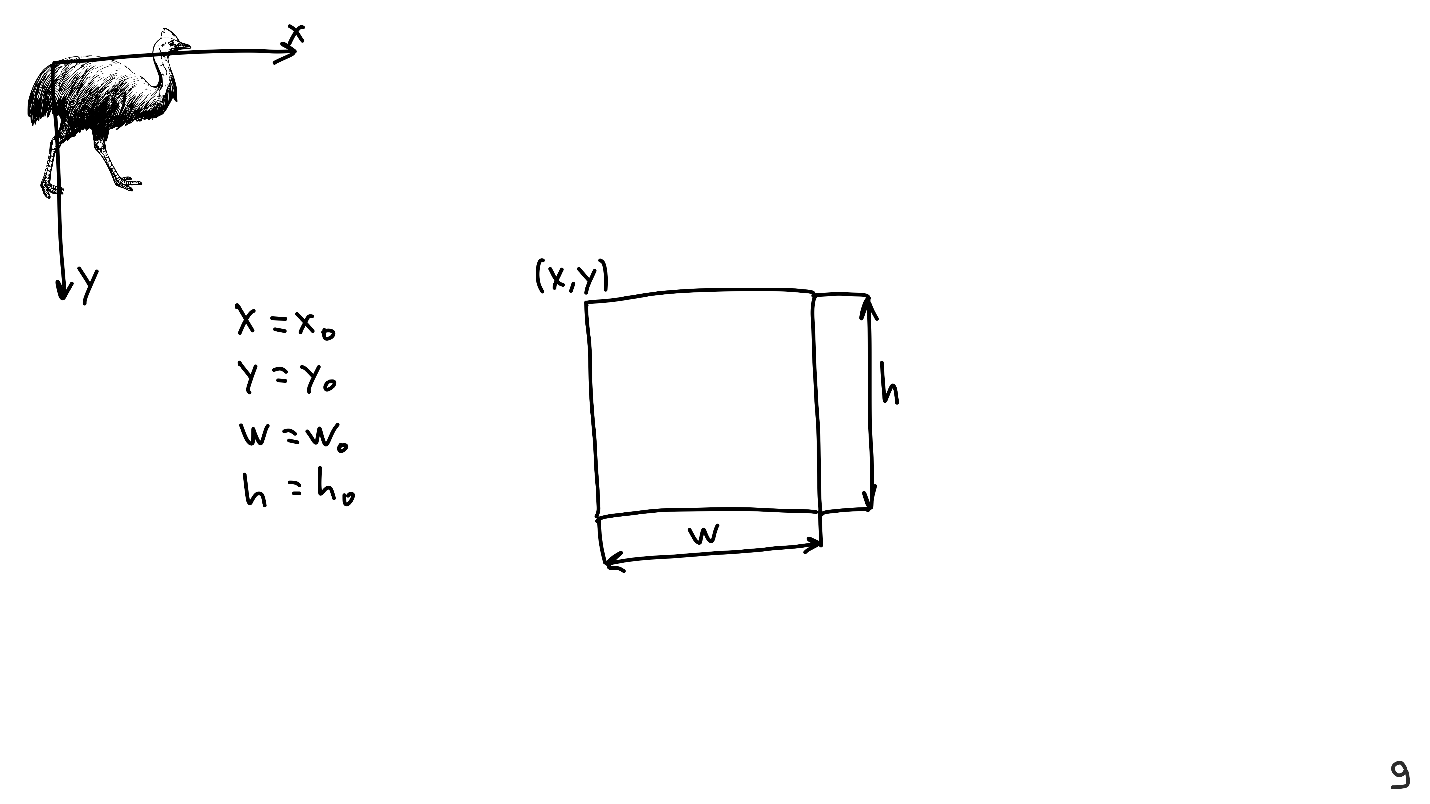
Conhecer esses quatro valores é suficiente para representar qualquer Visualização.

Algoritmo No. 1

Ao colocar o casuar na folha, descrevemos discretamente o primeiro algoritmo de layout:

• determinar as coordenadas e tamanhos;
• aplique-os ao UIView.

O algoritmo funciona, mas é bastante difícil de usar, por isso vamos simplificá-lo ainda mais.

Suponha que abaixo está uma solução para algum sistema de equações lineares.



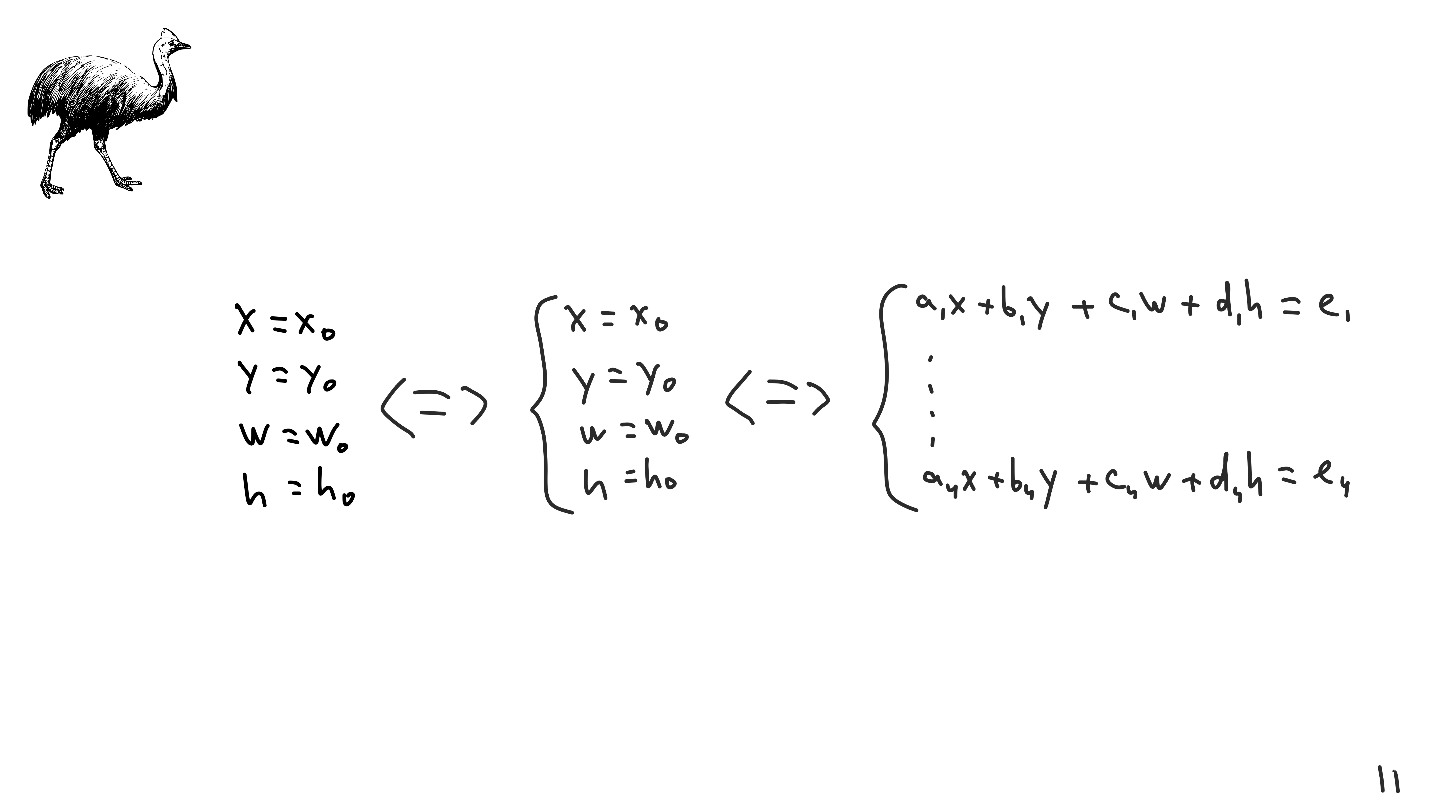
O sistema de equações lineares é especial, pois muitas operações são definidas sobre ele: dobrar linhas, multiplicá-las por constantes etc. Essas operações são chamadas de transformações lineares e, com a ajuda delas, o sistema é reduzido à forma arbitrária.

A beleza das transformações lineares é que elas são reversíveis. Isso nos leva a uma idéia interessante e bastante sutil com a qual todo o layout moderno começa.

Haja uma View - um retângulo com suas coordenadas e tamanho. Queremos organizá-lo para que o centro coincida com o ponto especificado. Modelamos o centro usando transformações lineares - a coordenada do canto superior esquerdo + metade da largura .



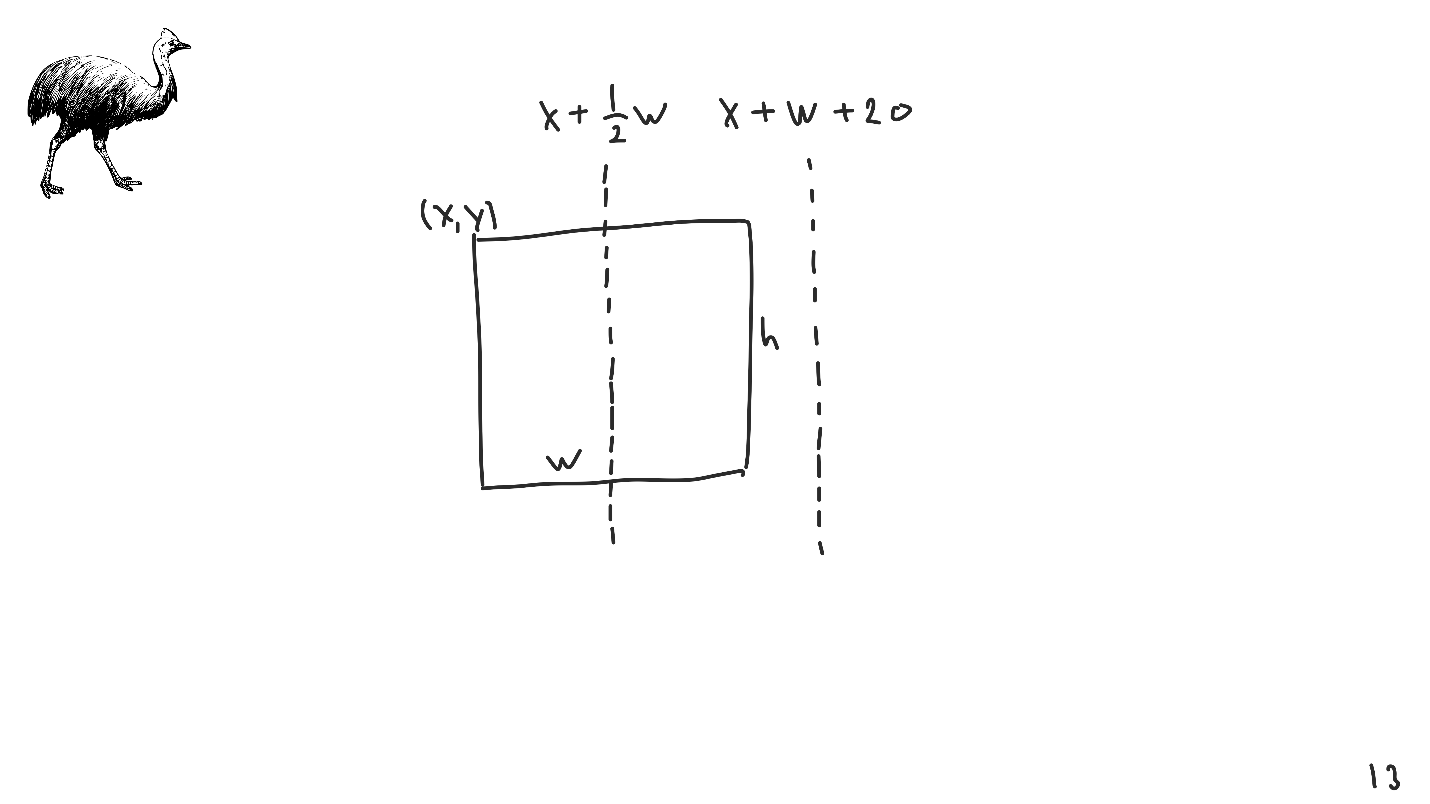
Modelamos o centro por transformação linear, não foi: havia apenas as coordenadas do ponto superior esquerdo, largura e altura.

Da mesma forma, você pode simular qualquer outro recuo, por exemplo, 20 pontos no canto direito.

É a idéia de transformações lineares que nos permite criar vários sistemas de composição tipográfica.

Considere um exemplo elementar. Escrevemos um sistema com o qual estabelecemos as coordenadas do meio e do lado direito, a largura e a relação entre largura e altura. Resolvemos o sistema e obtemos a resposta.



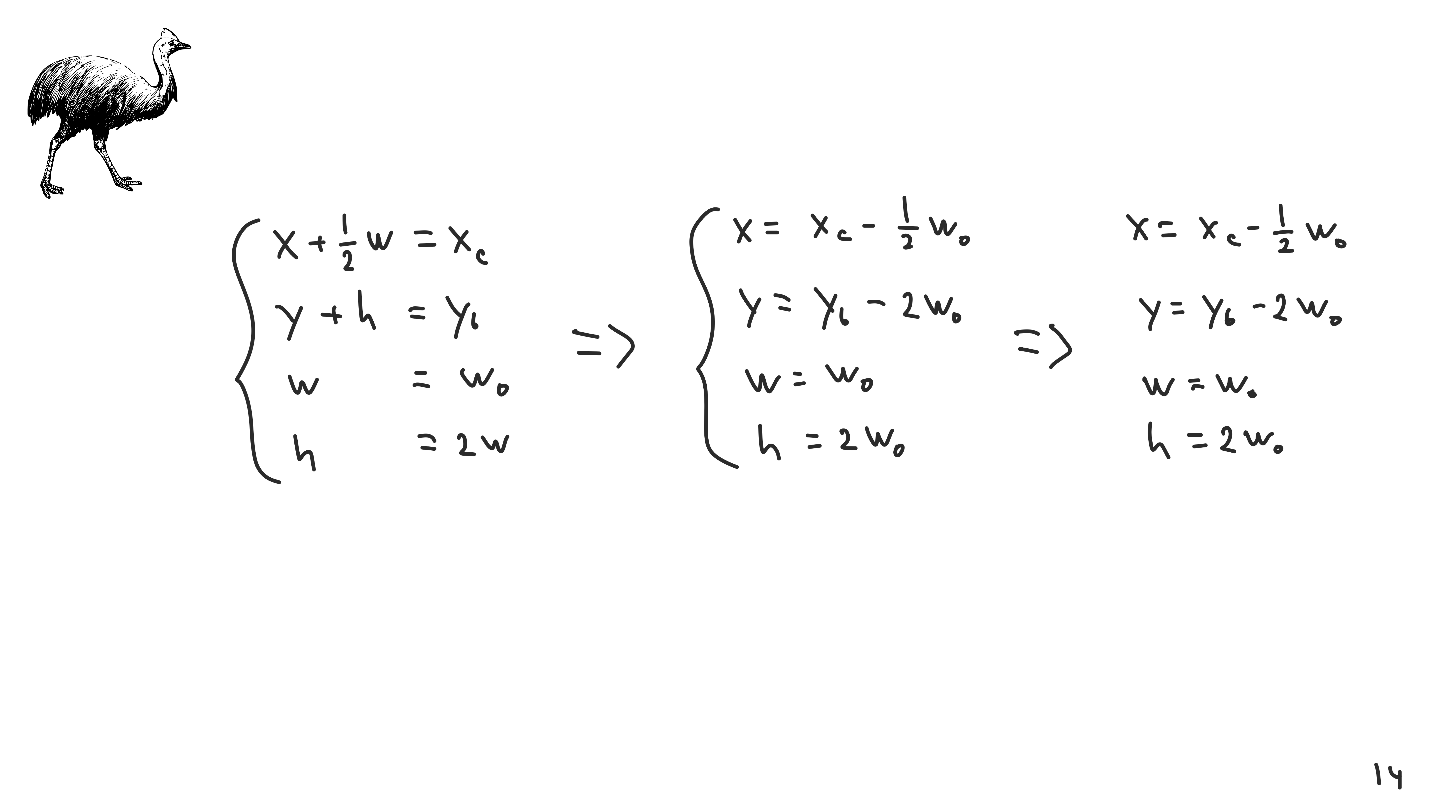
Então chegamos ao segundo algoritmo.

Algoritmo No. 2

A segunda iteração do algoritmo consiste nos seguintes itens:

• compor um sistema de equações lineares;
• nós resolvemos isso;
• aplique a solução ao UIView.

Imagine que estávamos no século XX, em uma época em que os equipamentos de informática estavam apenas começando, e fomos os primeiros a criar nosso próprio sistema de layout. Inventado, empacotado, dado ao usuário e ele começa a usá-lo - preenche os parâmetros iniciais e o transfere para o nosso sistema.



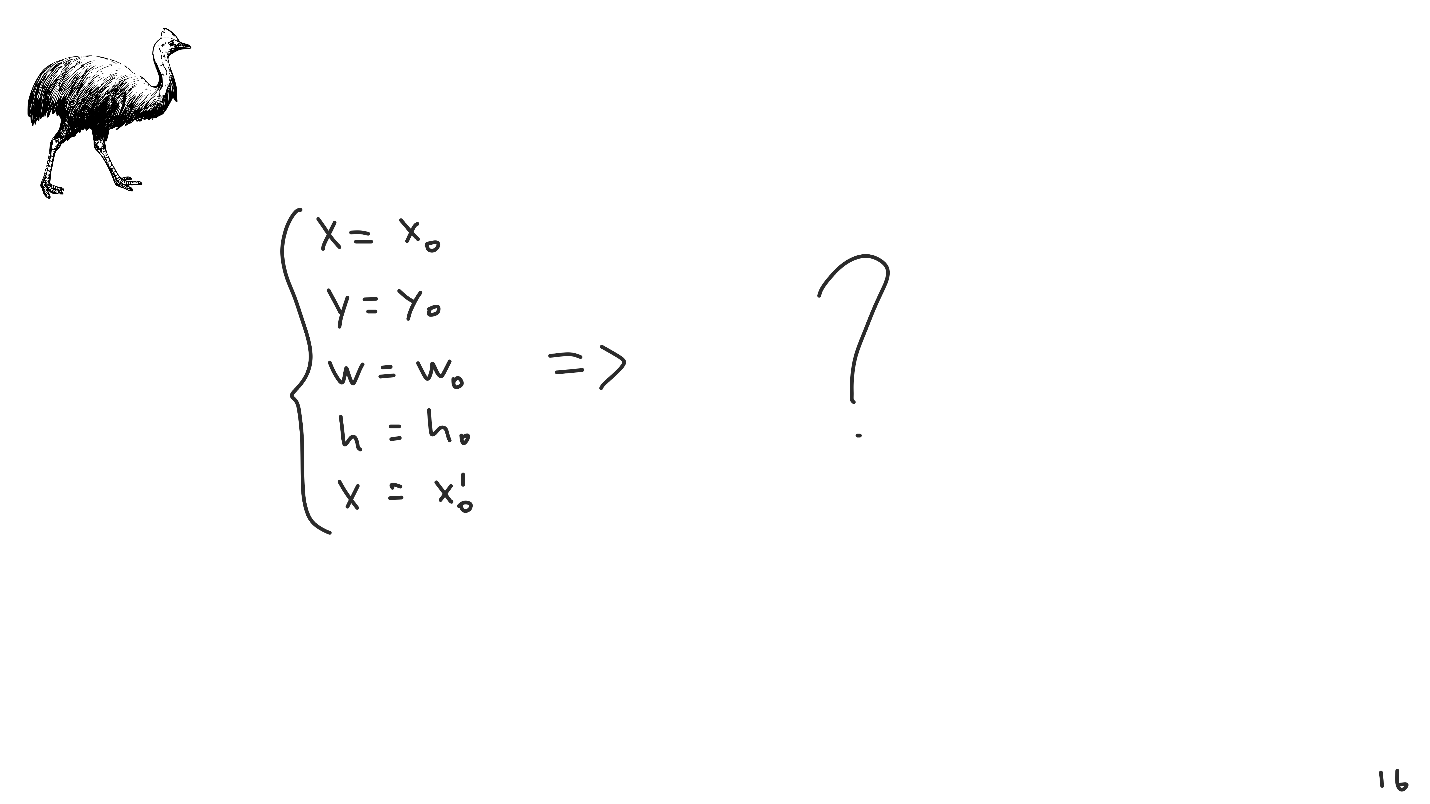
Há um problema - este sistema não possui uma solução única. O problema não é excepcional, absolutamente todos os sistemas de layout o enfrentam e é chamado de falta de solução .

Não há muitas maneiras de sair dessa situação:

• Você pode cair - este é um método muito comum. Quem trabalha com o MacOS sabe que o NSLayoutConstraintManager faz exatamente isso.
• Retorne o valor padrão . No contexto do layout, sempre podemos retornar todos os zeros.
• Uma maneira mais conhecida e delicada é impedir a entrada incorreta . Esse método é usado por sistemas populares de layout, por exemplo, Yoga , conhecido como Flex Layout . Esses sistemas tentam criar uma interface que não permita entrada incorreta.
• Há outra maneira de resolver absolutamente todos os problemas - repensar tudo desde o início e, inicialmente, evitar a ocorrência desse problema . O Layout automático foi por esse caminho.

Layout automático Declaração e solução do problema

Temos uma imagem retangular e, para identificá-la exclusivamente, precisamos de 4 parâmetros:

• coordenadas do canto superior esquerdo;
• largura e altura.

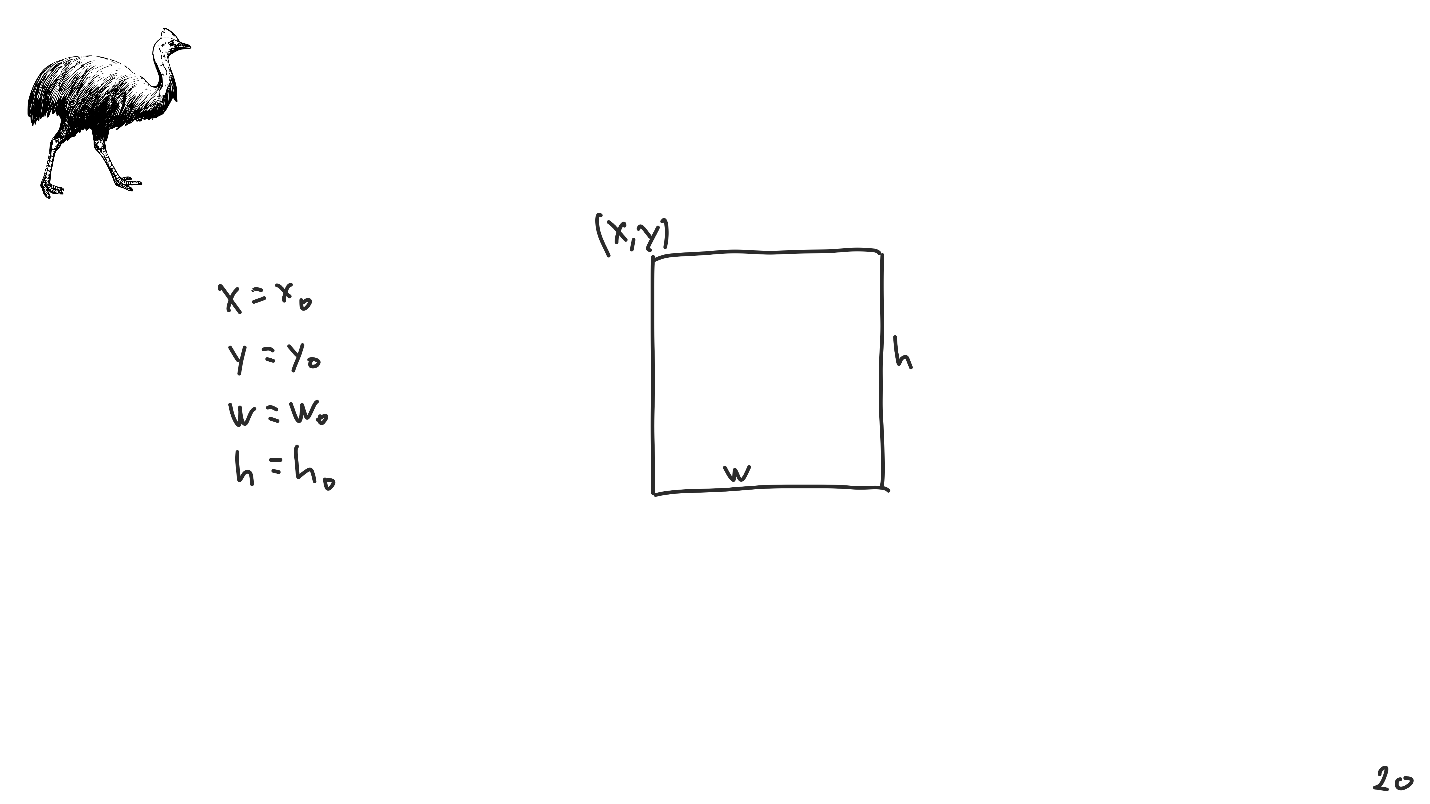
O layout automático é muito detalhado. Comparado a um sistema de equações lineares, é muito mais difícil colocar tudo na tela com ele. Portanto, consideraremos, sem perda de generalidade, o caso unidimensional.



Tudo é muito simples: o espaço é uma linha reta, e todos os objetos que podem ser colocados nele são pontos em uma linha reta. Um valor: X = X _{P é} suficiente para determinar a posição do ponto.

Considere a abordagem de layout automático. Há um espaço no qual as restrições são definidas. A solução que queremos obter é X = X ₀ , e nenhuma outra.

Há um problema - não definimos operações com restrições. Não podemos concluir diretamente do registro que X = X ₀ , não podemos multiplicar nada ou adicionar algo a nada. Para fazer isso, precisamos transformar a restrição no que podemos trabalhar - em um sistema de equações e desigualdades.



O Layout automático transforma um sistema de equações e desigualdades da seguinte maneira.

• Primeiro, introduz 2 variáveis ​​adicionais que não são negativas e dependem uma da outra . Pelo menos um deles é igual a zero.
• A restrição em si é convertida na notação X = X ₀ + a ⁺ - a ^- .

Ponto X ₀   - solução do sistema: se a ⁺ e a ^- são iguais a zero, isso será verdade. Mas qualquer outro ponto nessa linha será uma solução.

Portanto, é necessário encontrar o melhor entre todo o conjunto de soluções. Para fazer isso, introduzimos uma função - uma função comum que retorna um número e podemos comparar números. Desenhamos um gráfico e observamos que a solução que originalmente queríamos obter é mínima.

Tem um problema de programação linear . É exatamente isso que o Layout automático faz com restrições que não são apenas na forma de igualdades, mas também de desigualdades.

Restrições de desigualdade

No caso de restrições de desigualdade, a transformação ocorre da mesma maneira que nas igualdades: duas variáveis ​​adicionais são introduzidas e tudo isso é coletado no sistema. Somente o funcional é diferente e é igual a ^- .



O gráfico acima mostra por que é assim - qualquer valor de a ⁺ com a ^- = 0 (de X ₀ a + ∞ ) será a solução ideal para o problema.

Vamos tentar combinar essas duas restrições de equações e desigualdades em uma - como as restrições não vivem isoladas, elas são aplicadas juntas em todo o sistema.



Para cada restrição, um par adicional de variáveis ​​é introduzido e o funcional é compilado. Como queremos que todas essas restrições sejam cumpridas simultaneamente, o funcional será igual à soma de todos os funcionais de cada restrição .

Coletamos a função f e vemos que a solução é X ₁ . Como esperávamos, fazendo restrições. Então chegamos ao terceiro algoritmo.

Algoritmo No. 3

Para fazer algo, você precisa:

• criar um sistema de restrições lineares;
• transformá-lo em um problema de programação linear;
• resolver o problema de qualquer maneira conhecida, por exemplo, o método simplex usado no Layout automático;
• aplique a solução ao UIView.

Esse algoritmo parece ser suficiente, mas considere o seguinte caso: alteramos o conjunto inicial de restrições para que a segunda restrição agora seja X ≥ X ₂ .



Que solução esperamos ver?

• X ₁ ? De fato, na primeira restrição está escrito assim: X = X ₁ , e esta solução entra em conflito com a segunda restrição.
• X ₂ ? Já haverá um conflito com a primeira restrição.

Para sair da situação, realizaremos transformações que já sabemos fazer.

O gráfico da nova funcionalidade parece diferente: qualquer ponto do intervalo de X ₁ a X ₂ será a solução válida correta do sistema. Isso é chamado de incerteza .

Incerteza

O Auto Layout possui um mecanismo para resolver esses problemas - prioridades . Lembro que amarelo indica alta prioridade e azul - baixo.



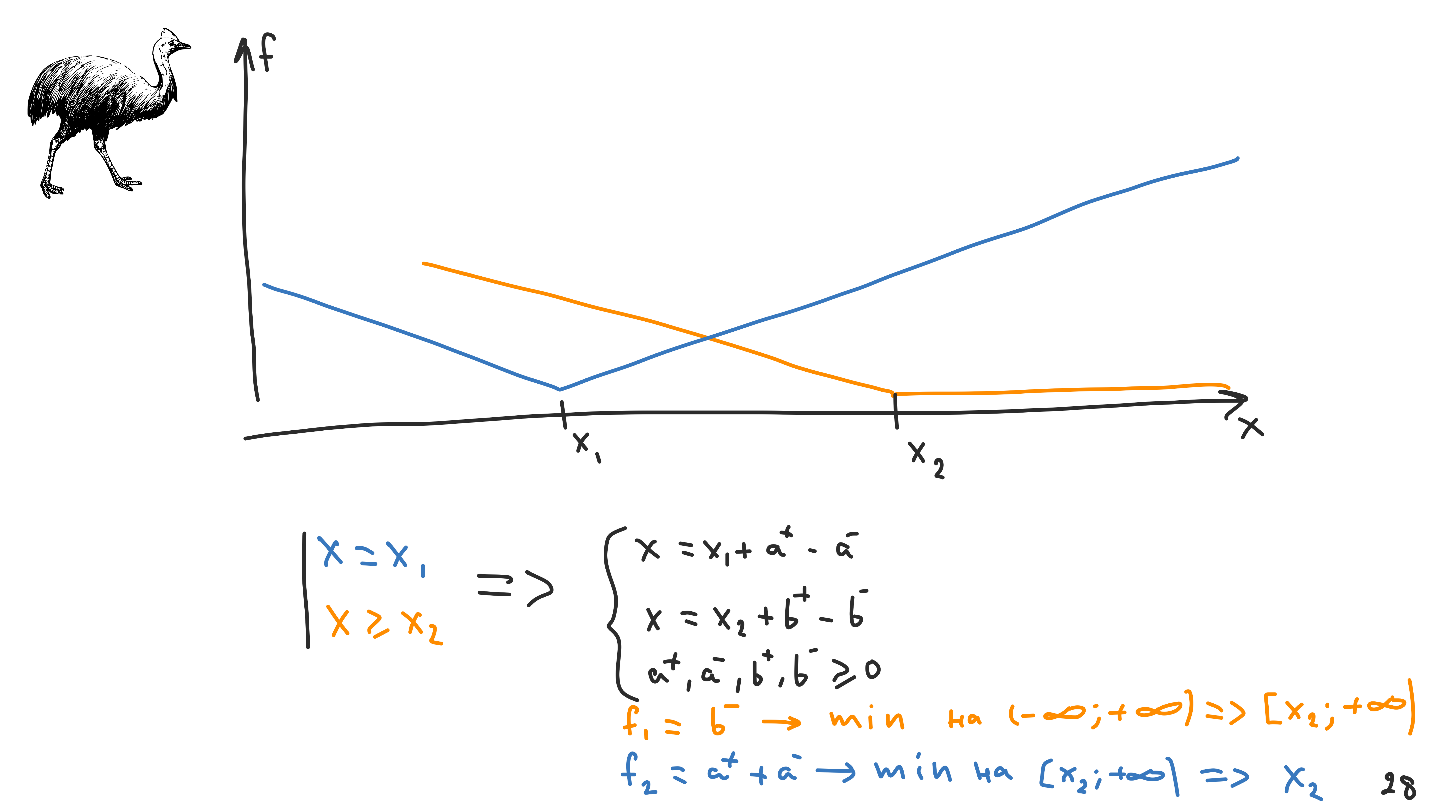
Converter restrições. Observe que o sistema resultante é apenas preto. Nós sabemos como trabalhar com ele e não há informações sobre restrições nele. Está nas funcionalidades, das quais haverá duas. O Layout automático minimiza primeiro o primeiro e depois o segundo.

Em problemas de programação linear, não estamos procurando a solução em si, mas a área de soluções viáveis. Obviamente, queremos que essa área seja apenas um ponto, e o Layout automático atua da mesma maneira. Primeiro, ele minimiza a funcionalidade de maior prioridade em ( - ∞, + ∞) e, na saída, recebe um domínio de soluções viáveis. O Layout automático resolve o segundo problema de programação linear já na faixa de valores permitidos obtida. Esse mecanismo é chamado de hierarquia de restrições e, neste problema, fornece o ponto X ₂ .

Algoritmo No. 4

• Crie uma hierarquia de restrições lineares;
• transformá-lo em uma tarefa de programação linear;
• resolver sequencialmente o problema de programação linear - da prioridade mais alta à mais baixa.
• aplique a solução ao UlView.

Vejamos a tarefa anterior novamente. Não somos matemáticos, mas engenheiros, e qualquer engenheiro deve ser confundido aqui.

Há um problema sério aqui - o infinito , e eu não sei o que é.

O algoritmo Cassowary, sob o capô do Layout Automático, não era um mecanismo existente que coubesse convenientemente à tarefa de Layout Automático, mas foi pensado como uma ferramenta de layout e forneceu mecanismos especiais para escapar do infinito desde o início. Para isso, vários tipos de restrições foram inventados:

• Parâmetros são as restrições com as quais trabalhamos. Eles são chamados de preferências no original , às vezes na documentação da Apple - restrições opcionais .
• Requisitos ou requisitos - restrições com prioridade necessária .

Vamos ver como os requisitos com essas prioridades são transformados do ponto de vista da matemática.



Novamente, temos uma linha reta com dois pontos, e a primeira restrição é X = X ₁ . No slide, é vermelha, ou seja, essa restrição com a prioridade necessária - chamaremos isso de requisito.

O Layout automático o converte em um sistema de equações lineares contendo uma equação X = X ₁ . Nada mais - sem tarefas de programação linear, sem otimizações.

A situação é semelhante às desigualdades, mas um pouco mais complicada - aparecerá uma variável adicional que pode assumir valores maiores que 0. Para qualquer valor maior que 0, essa restrição será atendida. Observe que aqui não há tarefas de programação linear e otimizações.

Vamos tentar combinar tudo isso, reunir dois requisitos e convertê-los em um sistema. Um leitor atento observou que chegamos ao mesmo problema com o qual começamos - os requisitos devem ser consistentes .



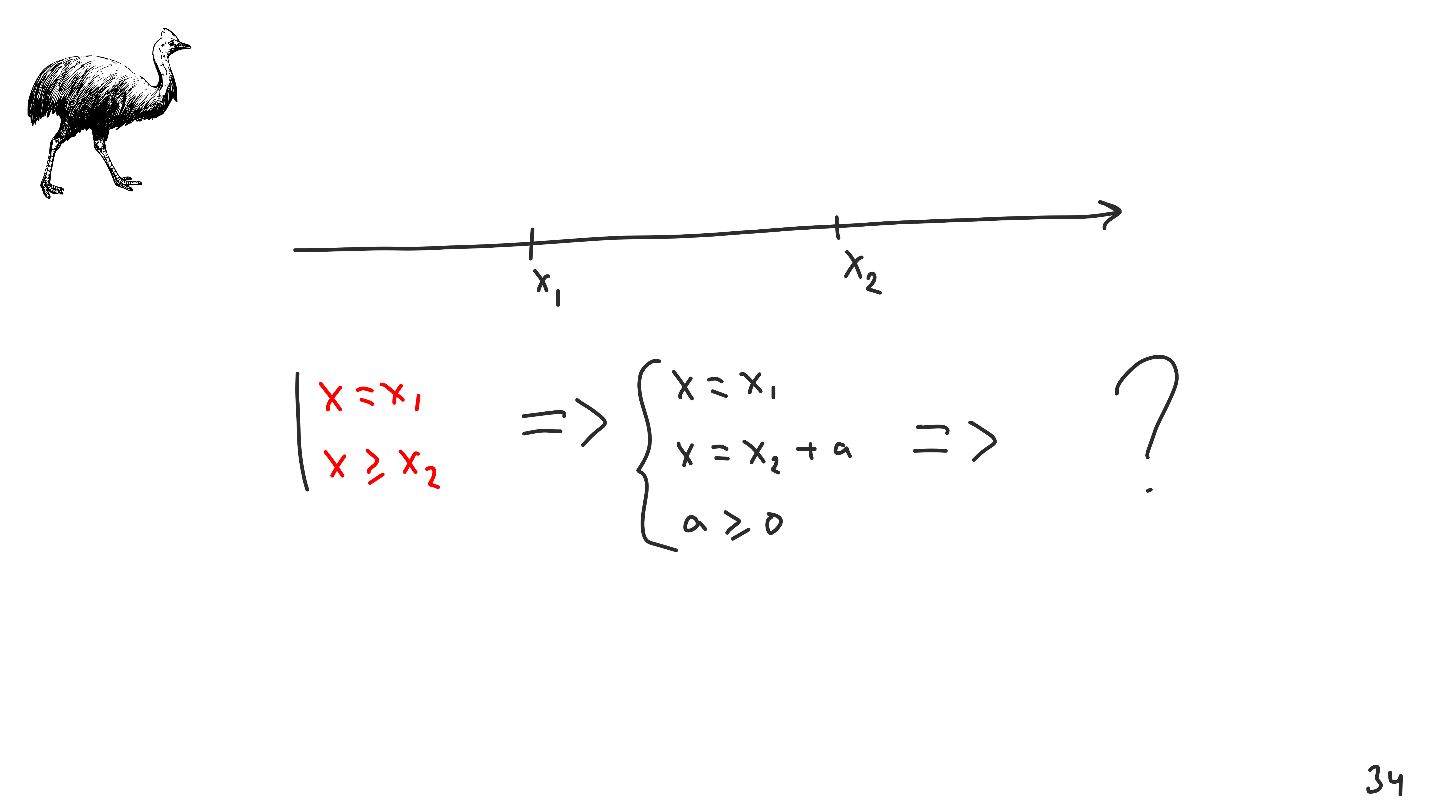
As restrições do tipo requerido ou requisitos são uma ferramenta muito poderosa, mas não a principal, mas a auxiliar. Foi especialmente introduzido no Auto Layout para resolver o problema de intervalos infinitos, e deve ser usado com cuidado.

Vamos tentar combinar todos os tipos de restrições que encontramos em um sistema. Suponha que queremos resolver o problema não em toda a linha, mas apenas entre X ₀ e X ₃ . Transformando tudo isso em um sistema de equações e desigualdades lineares, obtemos o seguinte.



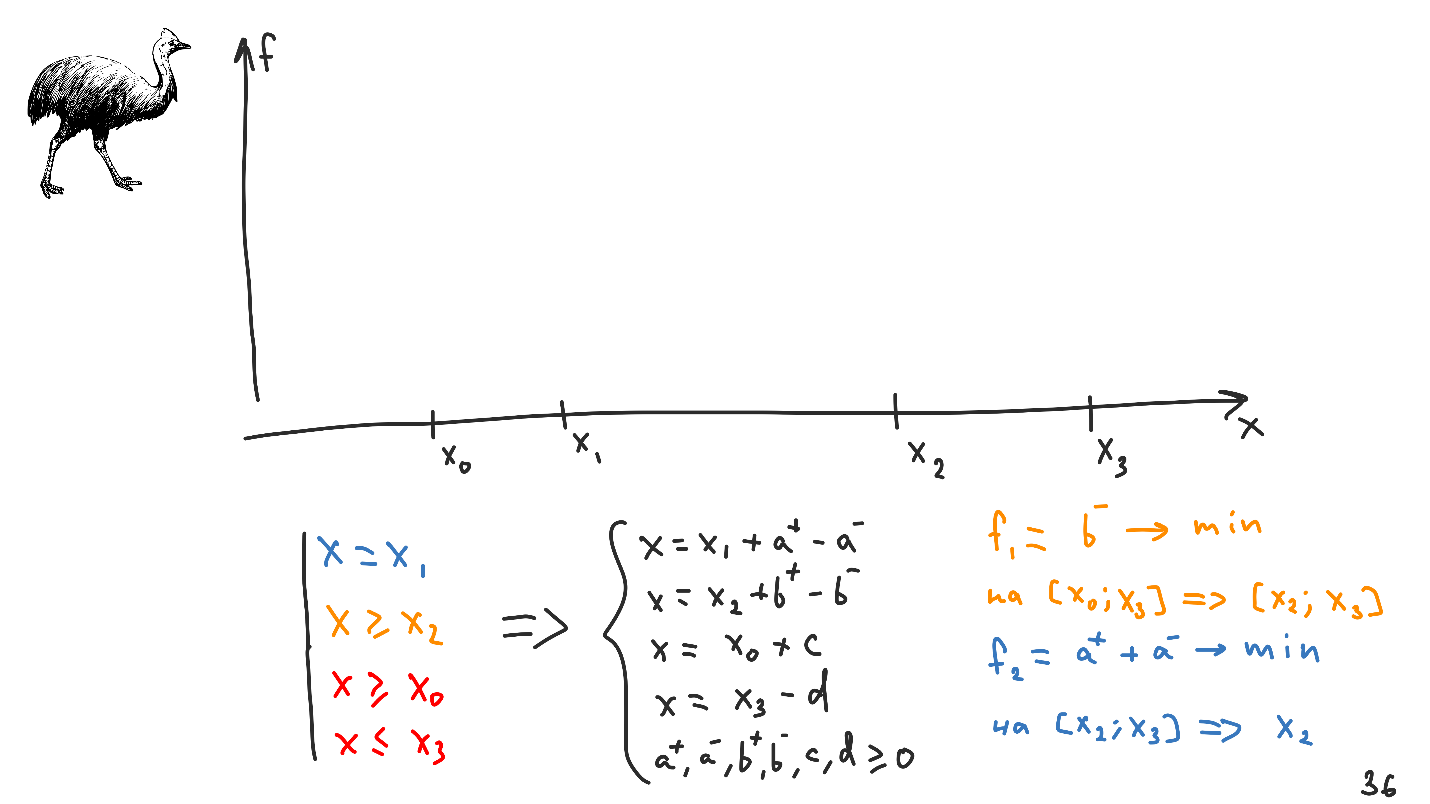
Em relação ao sistema anterior, duas variáveis ​​adicionais foram adicionadas - c e d , mas elas não entrarão nos funcionais, pois as restrições do tipo requerido não afetam o funcional em sua forma original.

Parece que a tarefa não mudou muito - minimizamos o mesmo de antes, mas o intervalo inicial de valores aceitáveis ​​está mudando, agora é de X ₀ a X ₃ .

Do ponto de vista matemático, os requisitos - restrições do tipo requerido - são a capacidade de introduzir equações adicionais no sistema sem modificar seus funcionais.

Você precisa ter muito cuidado com isso, pois o abuso excessivo das restrições necessárias levará a um problema sem soluções , e o Layout automático não lidará com isso.

Chegamos ao último quinto algoritmo.

Algoritmo No. 5

• Definir as restrições necessárias - requisitos de layout;
• criar uma hierarquia de restrições lineares;
• converter todas as restrições em um problema de programação linear;
• resolver o problema da programação linear;
• aplique a solução ao UlView.

Examinamos o Cassowary - um algoritmo que está dentro do Auto Layout, mas quando é implementado, vários recursos surgem.

Recursos do IOS

Não há cálculos no layoutSubviews () .

Quando eles são produzidos? Resposta: sempre, a qualquer momento, o Auto Layout é contado. O cálculo ocorre exatamente quando adicionamos restrições à nossa visualização ou as ativamos usando métodos modernos da API para trabalhar com restrições.



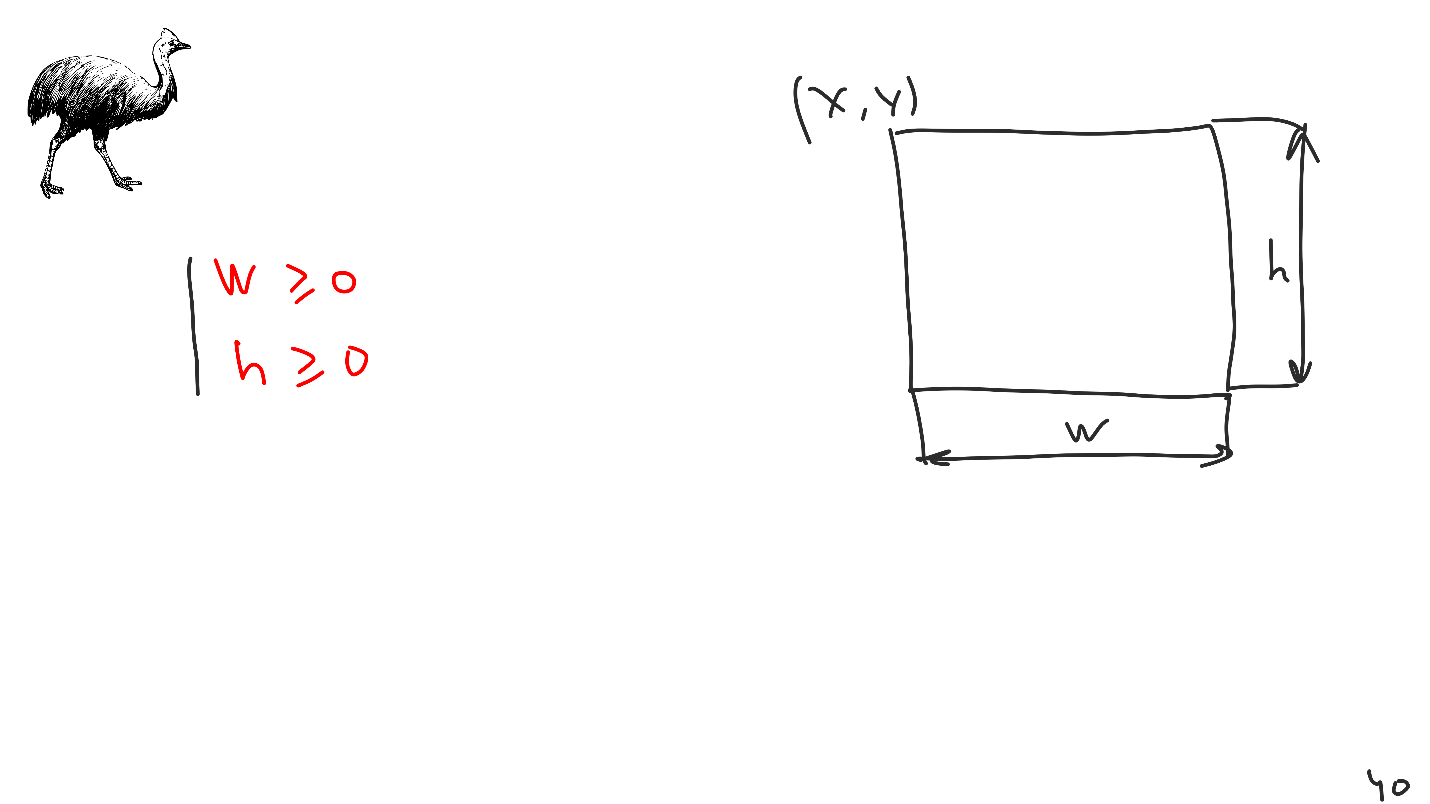
Nossas visões são retângulos, mas o problema é que essas informações não estão contidas no Cassowary, elas precisam ser incorporadas adicionalmente lá. Temos um mecanismo para introduzir restrições adicionais. Se introduzirmos para cada visualização um conjunto de restrições com largura e altura positivas, sempre obteremos retângulos na saída. É por isso que não podemos compensar a exibição de layout automático com dimensões negativas.

O segundo recurso é intrinsicContentSize - o tamanho intrínseco que pode ser definido para cada visualização.



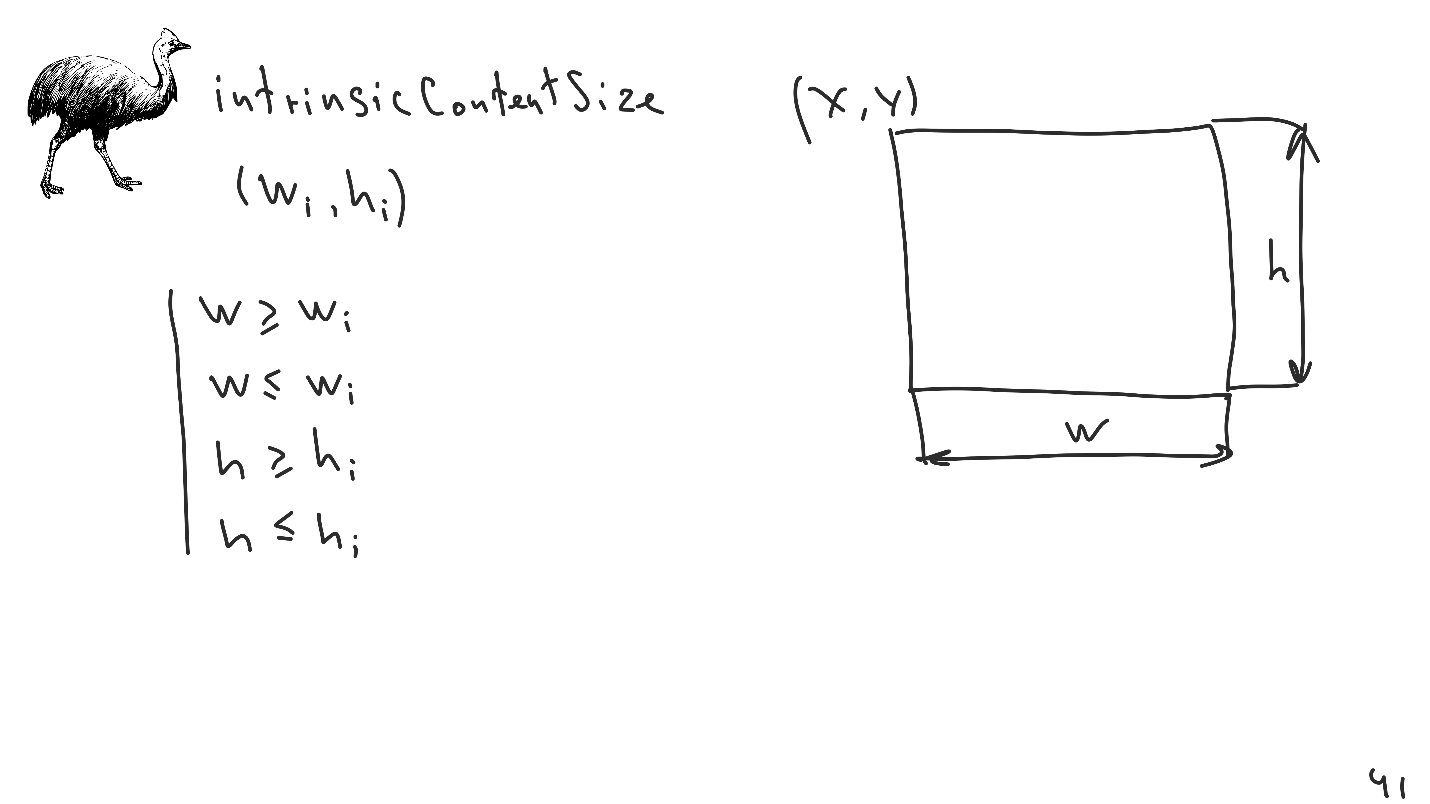
Essa é uma interface simples para criar 4 restrições adicionais de desigualdade que serão colocadas no sistema. Esse mecanismo é muito conveniente, pois permite reduzir o número de restrições explícitas, o que simplifica o uso do Layout Automático. O último e mais fino ponto que geralmente é esquecido é o TranslateAutoresizingMaskIntoConstraints.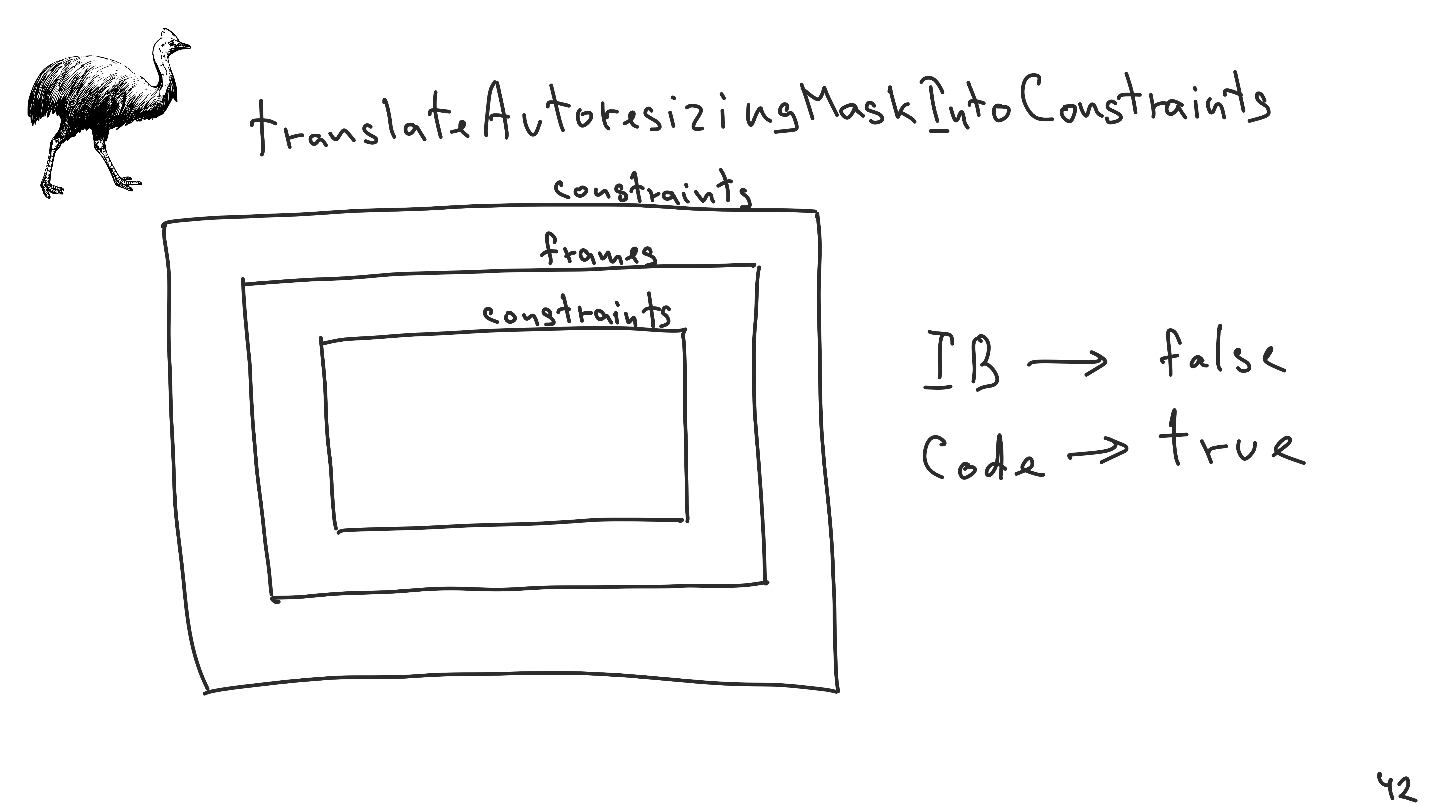



Esta é uma muleta que foi introduzida nos dias do iOS 5, para que o código antigo não seja quebrado após o aparecimento do Layout Automático.

Imagine uma situação: impomos uma visão sobre restrições. Dentro da view, usamos a view, que não sabe nada sobre restrições, tudo digitado em quadros, mas dentro dela ela digita a view, que há muito tempo se traduz em restrições.

Lembro que nenhum quadro entra na tarefa de Layout automático do Cassowary, apenas limitações.

O tamanho e a posição da vista que foi recolhida nos quadros não são totalmente determinados por restrições. Ao calcular o tamanho e a posição de todas as outras visualizações, os tamanhos incorretos serão levados em consideração, mesmo após o Layout automático, aplicaremos os quadros corretos.

Para evitar essa situação, se o valor da variável TranslateAutoresizingMaskIntoConstraints for verdadeiro, uma restrição adicional será aplicada a cada exibição que é apresentada no quadro. Esse conjunto de restrições pode variar de execução para execução. Apenas uma coisa é conhecida sobre esse conjunto - seu quadro será o que foi transmitido.

A compatibilidade entre o código antigo escrito sem restrições e o novo código escrito com restrições geralmente pode sofrer devido ao uso indevido dessa propriedade. Essas restrições necessariamente têm a prioridade dos requisitos; portanto, se subitamente impusermos restrições a essa visão, que possui uma prioridade muito alta, por exemplo, um requisito, podemos criar acidentalmente um sistema não consistente que não terá soluções.

É importante saber:

• Se criarmos uma visualização do Interface Builder , o valor padrão para essa propriedade será falso .
• Se criarmos a visualização diretamente do código, será verdade .

A idéia é muito simples - o código antigo no qual a visualização foi criada não sabia nada sobre o Layout Automático, e era necessário fazê-la para que, se a visualização fosse usada em algum lugar de um novo local, ele funcionaria.

Dicas práticas

Serão três conselhos no total e começarão pelos mais importantes.

Otimização

É importante localizar o problema.

Você já enfrentou o problema de otimizar a tela, que é apresentada no Layout automático? Provavelmente não, mais frequentemente você enfrentou o problema de otimizar o layout das células dentro de uma tabela ou de uma exibição de coleção .

O Layout automático é otimizado o suficiente para criar qualquer tela e interface, mas criar 50 ou 100 de uma vez é um problema. Para localizar e otimizar, vejamos o experimento. As figuras são retiradas de um artigo em que Cassowary foi descrito pela primeira vez.


A tarefa é a seguinte: criamos uma cadeia de visualizações uma a uma e conectamos cada uma delas à anterior. Assim, uma sequência de 1000 elementos foi construída. Após medir várias operações, o tempo é indicado em milissegundos. Os valores são bastante grandes, porque o Auto Layout foi inventado na junção dos anos 80 e 90.

Ao coletar essa cadeia, você pode agir da seguinte maneira:

• Adicione uma restrição de cada vez e decida cada vez. Isso levará 38 segundos.
• Você pode adicionar todas as restrições de uma só vez e só então resolver o sistema. Esta solução é mais eficiente. Segundo dados antigos, a eficiência aumenta em 70%, mas na implementação atual em dispositivos modernos haverá apenas 20%. Mas uma adição qualitativa única de restrições sempre será mais eficaz.
• Quando toda a cadeia é montada, você pode adicionar mais uma restrição . Como pode ser visto na tabela, esta operação é bastante barata.
• O mais interessante: se não adicionarmos novas restrições, mas alterar alguma constante em uma das existentes , essa é uma ordem de magnitude mais eficaz do que excluir ou criar uma nova restrição.

Os dois primeiros pontos podem ser descritos como o cálculo primário das interfaces, os dois últimos - como o próximo.

Cálculo da interface primária

Aqui você pode usar os métodos de adição em massa de restrições para otimização:

• NSLayoutConstraints.activate (_ :) - ao criar uma exibição, colete todas as restrições seqüencialmente em uma matriz, faça cache e adicione-as de cada vez.
• Ou crie células no Interface Builder. Ele fará tudo por nós e realizará otimizações adicionais, o que geralmente é conveniente.

Cálculos subsequentes da interface

Adicionar ou modificar restrições é uma operação complexa; portanto, é melhor não alterar o conjunto de restrições, mas apenas alterar as constantes nas restrições existentes. :

• UIView — . view , Auto Layout. , , view, .
• — IntrinsicContentSize. , , .
• . , , .

, WWDC 2018S220 High Performance Auto Layout . — Apple , .

, constraints.

required , — , , . .

, .

:

• , . ( loader) — .
• , . , .

, , .

constraint required, . , , , . , .

— , . , — . - , , . Auto Layout , .

, . . , , , . layout, , , . .

— , Auto Layout, , .

, required, , . :

• , .
• , , .

, , , .

, . , , , . , — . .

— . , , , — , — required -.

:

Solving Linear Arithmetic Constraints for User Interface Applications
The Cassowary Linear Constraint Solving Algorithm
Constraints as s Design Pattern
Auto Layout Guide by Apple
WWDC 2018 Session 220 High Performance Auto Layout
UILabel API Auto Layout —
. Medium

A propósito, já aceitamos o relatório de Anton no programa AppsConf 2019 . Gostaria de lembrá-lo de que mudamos o AppsConf do outono para a primavera, e a próxima conferência mais útil para desenvolvedores móveis será realizada nos dias 22 e 23 de abril. É hora de pensar no tópico para apresentação e enviar um relatório ou discutir com o líder a importância de ir à conferência e reservar um ingresso.