História do Shipastik

Picos em todos os lugares

Nós o chamamos de Spikey, e hoje em minha vida eu o encontro constantemente:



Ele vem de um objeto tridimensional, um poliedro chamado "rômbico sexagésimo".



Mas qual é a sua história e por que fizemos disso nosso símbolo?

A origem do espinho

Em 1987, quando desenvolvíamos a primeira versão do Mathematica, uma de suas inovações era a possibilidade de gerar gráficos tridimensionais independentes de resolução com base em descrições simbólicas. Nas primeiras demonstrações, isso nos permitiu produzir imagens surpreendentemente claras de poliedros regulares. Mas, aproximando o lançamento do Mathematica 1.0, queríamos usar um exemplo mais impressionante. Portanto, decidimos pegar o último poliedro regular - o icosaedro - e tornar algo mais complexo, dando-lhe uma forma de estrela ou, mais corretamente, acumulação. Sim, é assim que era a primeira interface de notebook há 30 anos.



No início, foi apenas uma demonstração agradável que funcionou muito rapidamente em nossos computadores da época. Mas logo o objeto tridimensional gerado por ele começou a ser de fato usado como um logotipo para o Mathematica. E quando a versão 1.0 foi lançada em 1988, o icosaedro estrelado estava em todo lugar:



Com o tempo, várias dedicatórias ao poliedro estelar começaram a aparecer - feitas em diferentes materiais e tamanhos:



Porém, apenas um ano após o lançamento do Mathematica 1.0, estávamos prontos para lançar o Mathematica 1.2 e, para transmitir a complexidade do produto, precisávamos de um logotipo sofisticado. Um de nossos desenvolvedores, Igor Rivin, defendeu sua tese de doutorado sobre poliedros no espaço hiperbólico - e, graças a seus esforços, os materiais da versão 1.2 foram decorados com um icosaedro hiperbólico:



Meus funcionários me deram uma camiseta com o moderno Shipastik para meu aniversário de 30 anos em 1989, e uma citação que eu apoio mesmo depois de tantos anos:


“Empresa é divertida”

Após o lançamento do Mathematica 1.2, em nossos materiais de marketing, foi possível encontrar uma coleção inteira de poliedros hiperbólicos regulares, mas com o advento da versão 2.0 em 1991, decidimos que gostávamos mais do icosaedro hiperbólico:



Mas continuamos a explorar outras formas pontiagudas. Inspirado no desenho de Leonardo da Vinci de um "modelo de madeira" do icosaedro estrelado (feito com perspectiva surpreendentemente exata) para o livro "On Divine Proportion" de Luke Pacioli , pedimos um pôster da versão 2.0 onde cinco tetraedros interseção são organizados de modo que seus vértices externos se formem no dodecaedro:



Hoje, examinando meus arquivos de 1991, encontro o código "explicativo" e é bom ver que ele é facilmente executado em nossa versão mais recente do Wolfram Language (embora hoje possa ser escrito de forma um pouco mais elegante):



Ao longo dos anos, isso se tornou um ritual estranho - em preparação para o lançamento da próxima versão principal do Mathematica, organizaremos reuniões sérias onde estamos envolvidos na “escolha de um novo Shipastik”. Às vezes, você precisa escolher entre centenas de opções diferentes criadas usando algoritmos completamente diferentes:



Mas, embora as paletas de cores estejam mutantes e os Shipastiks frequentemente reflitam a presença de novos recursos no sistema (embora de forma implícita), temos uma tradição de 30 anos na escolha de opções para um dodecaedro hiperbólico:



Recentemente, tornou-se habitual estudar o espaço paramétrico - embora agora já tenhamos acumulado centenas de parâmetros:



O dodecaedro hiperbólico tem 20 picos - era ideal para comemorar o 20º aniversário da Mathematica em 2008. Mas quando queríamos fazer algo semelhante para o 25º aniversário de 2013, fomos confrontados com o problema da falta de poliedros regulares com 25 vértices. Mas (de fato, usando a função SpherePoints [25]), conseguimos criar uma figura aproximada e imprimi-la em uma impressora 3D para todos os funcionários da empresa, com tamanhos correspondentes ao tempo de serviço dos funcionários.

Saída Wolfram | Alpha

Em 2009, estávamos nos preparando para o lançamento do Wolfram | Alpha, e o sistema precisava de um logotipo. Havia muitos conceitos:



Queríamos enfatizar que o Wolfram | Alpha funciona por meio de cálculos, e não, digamos, como um mecanismo de pesquisa. E por algum tempo nós queríamos usar algo com engrenagens. Mas também queríamos que o logotipo se parecesse com o logotipo de longa data da Mathematica. Isso deu origem a um desses projetos como "nosso general enlouqueceu": a criação de um mecanismo de engrenagem a partir de formas pontiagudas.

Um usuário de longa data do Mathematica e Wolfram Language, um engenheiro mecânico da Hungria, Sandor Kabai, nos ajudou a propor “engrenagens com pontas”:



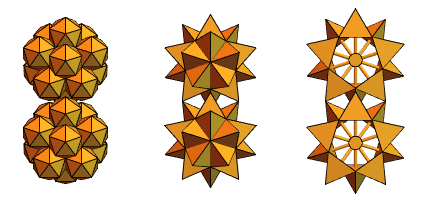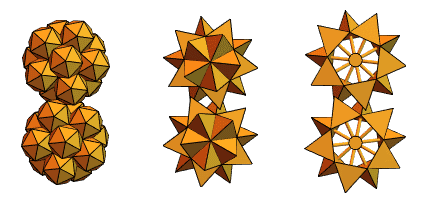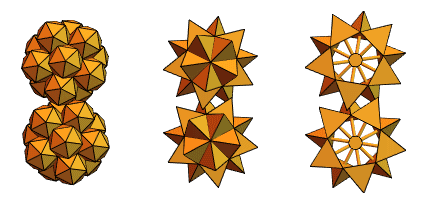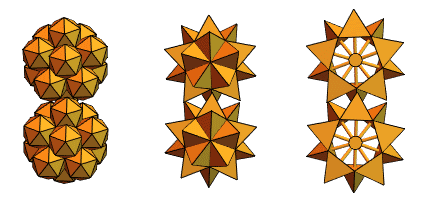
Voltando aos tetraedros que se cruzam a partir da versão 2, ele criou algo assim:



Em 2009, as impressoras 3D se tornaram muito populares, e nós pensamos que seria bom criar um logotipo para Wolfram | Alpha que pudesse ser impresso. O poliedro hiperbólico não se encaixava - os picos podiam se romper e constituir uma ameaça. Formas como picos da 4ª versão, com "picos seguros", careciam de elegância.

Por um tempo, nos apegamos a uma idéia com engrenagens. Mas no final, eles decidiram que valia a pena dar uma outra olhada nos poliedros comuns. Mas qual poliedro podemos escolher?

Obviamente, há um número infinito de possíveis poliedros. Mas para o nosso logotipo, queríamos escolher um poliedro simétrico e, até certo ponto, "certo". Cinco poliedros regulares (ou "sólidos platônicos") - cujas faces são os mesmos polígonos regulares - podem ser considerados os "mais regulares" de todos:



Existem mais 13 corpos arquimedianos - eles têm vértices idênticos e polígonos regulares, embora de tipos diferentes, atuam como faces:



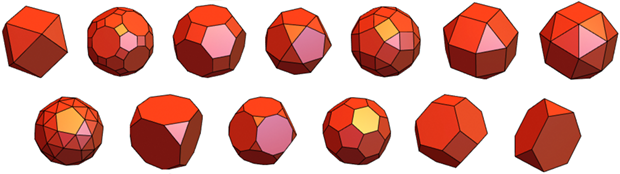
Existem muitos tipos de “correção” de poliedros. Um exemplo é o "poliedro homogêneo" que um pôster do The Mathematica Journal de 1993 mostra:



Ao longo dos anos em que Eric Weinstein colecionou a coleção, que em 1999 havia se transformado no MathWorld, ele tentou incluir artigos sobre o maior número possível de polígonos. Em 2006, como parte da inclusão de vários dados sistematizados no Mathematica e Wolfram Language, começamos a incluir dados poligonais no MathWorld. Como resultado, após o lançamento da versão 6.0 em 2007, a função PolyhedronData apareceu nela, que continha dados abrangentes sobre 187 polígonos notáveis:



No Mathematica e na Wolfram Language, você sempre pode gerar polígonos regulares, mas agora ficou mais fácil fazer isso. Com a versão 6.0, também lançamos o Wolfram Demonstrations Project, que rapidamente começou a ser reabastecido com várias demos relacionadas ao poliedro.

Uma delas foi feita pela minha filha Katerina aos 10 anos (hoje ela continua a se desenvolver nos campos da geometria): são os "coalas poliédricos", divididos por todos os poliedros do PolyhedronData [] usados:



Nesse contexto, em 2009, queríamos “escolher um poliedro” para o Wolfram | Alpha. Tudo foi decidido na sexta-feira, 6 de fevereiro, quando comecei a trabalhar por conta própria.

Preservei esse caderno e mostra que primeiro tentei implementar a idéia dúbia de colocar esferas nos vértices dos poliedros:



Mas, como registrado no histórico do notebook , apenas dois minutos depois, mudei para poliedros puros - eram todos alaranjados, que então queríamos usar para o logotipo:





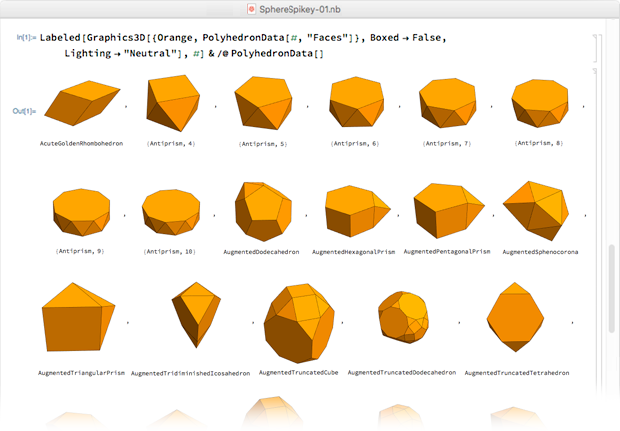
Os poliedros foram organizados em ordem alfabética por nome e na 28ª linha ele apareceu - um hexaedro rômbico.



Alguns minutos depois, às 00:24:24 de 7 de fevereiro de 2009, descobri esse hexaedro rômbico e o transformei em uma posição simétrica, que usamos agora:



Queria ver como ficaria em cinza e em silhueta e, quatro minutos depois, usei o ColorSeparate para descobrir:



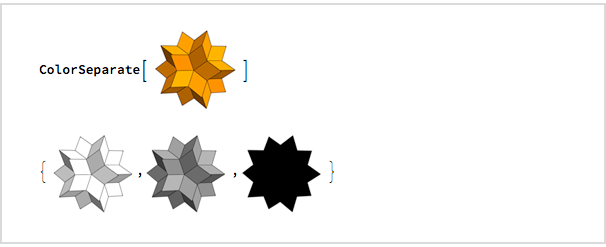
Imediatamente comecei a escrever um e-mail enviado às 00:32:

Eu realmente gosto do RhombicHexecontahedron. Tem uma forma interessante e muito simétrica. Parece-me que sua precisão nos convém, e a silhueta parece bastante razoável.



Obviamente, acabei de copiar o RhombicHexecontahedron do caderno (duvido que eu pudesse ter escrito o hexágono [hexecontahedron] sem erros). Nos meus arquivos, sei que essa foi a primeira vez que escrevi o nome do poliedro, que está destinado a se tornar o meu favorito.

No Wolfram Language, era muito fácil obter uma imagem de um hexaedro rômbico e brincar com ele:



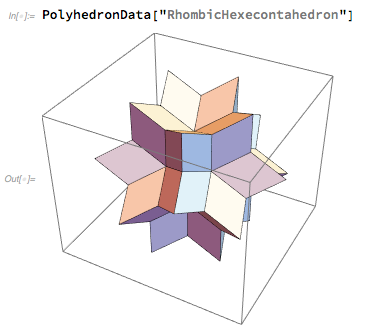
Na segunda-feira, estava claro que o hexaedro rômbico havia vencido - e nosso departamento visual estava ocupado desenhando-o como um logotipo para Wolfram | Alpha. Tentamos várias orientações, mas no final decidimos a posição simétrica "à vista de todos" que eu escolhi. (Também precisamos escolher a melhor “distância focal” para o ângulo mais adequado).



Como nosso icosaedro estrelado da versão 1.0, o hexaedro rômbico tem 60 faces. Mas de alguma forma, graças às combinações de “cinco pétalas”, parece muito mais elegante. Foi gasto um grande esforço na escolha de um sombreamento das faces para que o desenho bidimensional refletisse corretamente o objeto tridimensional. Mas logo introduzimos a primeira versão oficial do nosso logotipo:



Ela rapidamente começou a aparecer em todos os lugares e, como uma homenagem às nossas primeiras idéias, muitas vezes contra um fundo decorado com engrenagens:



Alguns anos depois, corrigimos levemente o sombreamento das bordas, o que levou à criação do logotipo Wolfram | Alpha, que ainda está em uso:



Hexágono rômbico

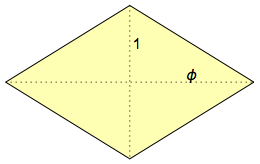
O que é um hexaedro rômbico? Em inglês, é chamado hexecontahedron, porque possui 60 faces, e ἑξηκοντα (hexekont) é a palavra grega para "60". As suas faces são losangos dourados , assim denominados porque as suas diagonais se relacionam de acordo com a proporção áurea: φ = (1 + √5) / 2 & sime; 1.618:



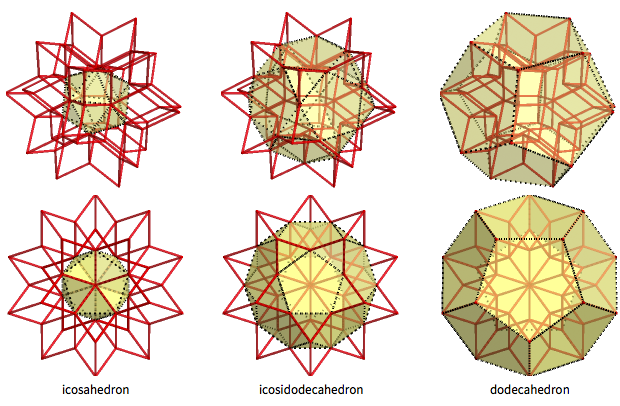
O hexaedro rômbico é um corpo intermediário interessante entre o icosaedro e o dodecaedro (com o icosododecaedro entre eles). Os 12 vértices internos do hexaedro rômbico formam o icosaedro regular e os 20 vértices externos formam o dodecaedro regular. 30 "picos intermediários" formam o icosododecaedro, de 32 facetas (possui 20 faces triangulares e 12 pentagonais):



No total, o hexaedro rômbico possui 62 vértices e 120 arestas (além de 120-62 + 2 = 60 faces). Possui três tipos de vértices (“interno”, “médio” e “externo”), correspondentes a 12 + 30 + 20 vértices do icosaedro, icosododecaedro e dodecaedro. Nesses vértices 3, 4 e 5, as arestas convergem juntas, respectivamente. Cada face possui um vértice "interno" no qual 5 arestas se encontram, um vértice externo onde três arestas se encontram e dois "intermediário" onde 4 arestas se encontram. Os vértices externo e interno são os vértices de ângulo agudo dos losangos dourados e os intermediários são de ângulo obtuso.

O ângulo nos picos pontiagudos dos losangos dourados é de 2 tan ⁻¹ (φ ⁻¹ ) ≈ 63,43 °, e nos picos pontiagudos é de 2 tan ⁻¹ (φ) ≈ 116,57 °. Esses ângulos permitem montar um hexaedro rômbico do construtor Zometool usando apenas os suportes vermelhos (como no caso do dodecaedro):



Das 120 arestas do hexaedro rômbico de 60 “dobradiças internas”, o ângulo diédrico é de 4π / 5 = 144 ° e para 60 externas é de 2π / 5 = 72 °. Os ângulos contraídos pelos vértices externo e interno são π / 5 e 3π / 5.

Para desenhar um hexaedro rômbico, é necessário conhecer as coordenadas tridimensionais de seus vértices. Eles são convenientemente obtidos usando o fato de o hexaedro rômbico ser invariável em relação ao grupo icosaedro, para que você possa começar com um losango dourado e simplesmente adicionar 60 matrizes que formam uma representação tridimensional do grupo icosaedro. Isso, por exemplo, fornece as coordenadas finais dos vértices em {± φ, ± 1,0}, {± 1, ± φ, ± (1 + φ)}, {± 2φ, 0,0}, {± φ, ± ( 1 + 2φ), 0}, {± (1 + φ), ± (1 + φ), ± (1 + φ)} e suas permutações cíclicas com todos os sinais possíveis.

Além do fato de que as faces de um hexaedro rômbico são losangos dourados, um hexaedro rômbico pode ser construído a partir de 20 romboedros dourados (nos quais todas as seis faces são losangos dourados):



Existem outras maneiras de criar um hexaedro rômbico a partir de outros poliedros. Pode ser obtido a partir de cinco cubos que se cruzam e de 182 dodecaedros em contato com as faces:



Você não pode criar um mosaico contínuo de sessenta e hexaedros rômbicos, mas eles se encaixam bem um com o outro (e, sim, vi dezenas de Shipastiks de papel dobrando-se dessa maneira):



Você também pode fazer todos os tipos de anéis e outras configurações a partir deles:



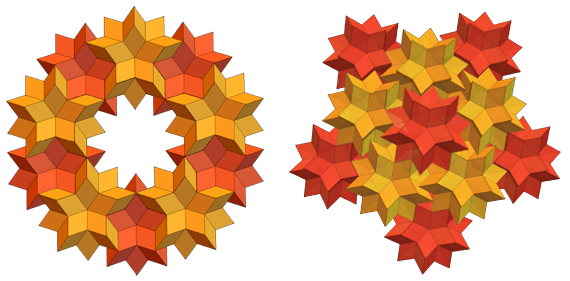
Um parente próximo do hexaedro rhombic (RS) é o trinta-tetrahedron rhombic (RT). RS e RT têm rostos que são losangos dourados. Mas o RS tem 60 deles e o RT tem 30. Veja como é um RT separado:



Vários RTs são perfeitamente investidos em bolsos RS, e coisas semelhantes acontecem:



Sandor Kabay, mencionado anteriormente, interessou-se pela RSh e RT por volta de 2002. E após o lançamento do Projeto de Demonstrações Wolfram, ele, juntamente com o matemático esloveno Isidor Hafner, adicionou mais de cem demonstrações ao projeto relacionado ao RS, RT e muitas de suas propriedades:

Modelos de papel pontudo

Assim que decidimos que Shipastik seria um RS, começamos a fazer seus modelos 3D. Agora é muito simples fazer isso usando a função Printout3D [PolyhedronData [...]], e modelos já calculados podem ser encontrados em recursos de terceiros .

Em maio de 2009, quando o Wolfram | Alpha foi lançado, já tínhamos muitos Spikes 3D em mãos:



Mas, nos preparando para a primeira temporada de férias após esse evento, decidimos dar a todos a oportunidade de fazer seu próprio Shipastik tridimensional. Primeiro, consideramos a opção com 20 ímãs romboédricos revestidos com plástico. Mas eles saíram caros e não se uniram muito bem.

Isso nos levou à ideia de fazer o Shipastik sem papel ou papelão fino. Portanto, a princípio, queríamos fazer um esquema que pudesse ser dobrado no Shipastika:



Minha filha Katerina serviu como testadora (e ela ainda tem uma amostra), mas ficou claro que muitas situações desconfortáveis ​​aparecem no processo de dobragem, nas quais não está claro como mudar de uma posição para outra. Você pode criar um grande número de layouts (existem 43.380 deles apenas para o dodecaedro e o icosaedro) - e pensamos que talvez fosse possível escolher algo melhor deles:



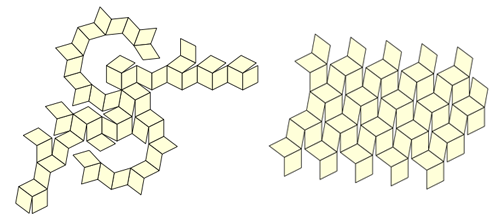
Mas, quando não conseguimos encontrar esse esquema, tivemos uma nova idéia (embora óbvia): se o modelo se agarrava aos ouvidos, por que não fazê-lo em poucas partes? Logo percebemos que, para isso, você precisa pegar apenas 12 peças idênticas desse tipo:



Com a ajuda deles, criamos nossos " conjuntos para esculturas de papel ":



Uma tarefa interessante foi escrever instruções fáceis de entender, mas após várias iterações, as instruções tornaram-se bem desenvolvidas e simples:



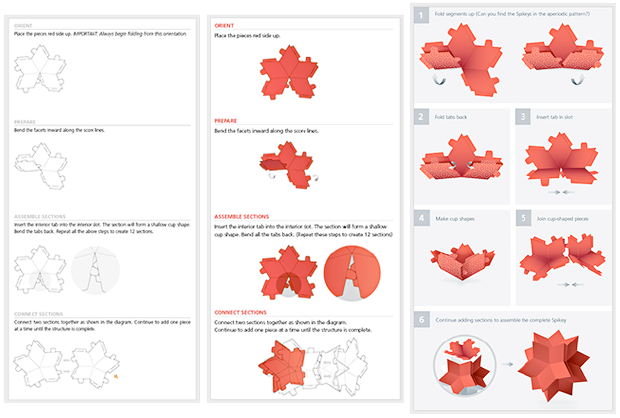
E depois que o Shipastiks foi enviado às pessoas, nossos usuários começaram a nos enviar todos os tipos de imagens do Shipastik “no chão”:

O caminho para o hexágono rômbico

O cubo multifacetado do Egito antigo

Não se sabe quem primeiro descreveu os sólidos platônicos. Talvez isso tenha sido feito pelos pitagóricos (que moravam perto de grandes depósitos de cristais de pirita multifacetados). Talvez alguém tenha feito isso muito antes deles. Talvez fosse um contemporâneo de Platão, Teetet de Atenas . Mas, em qualquer caso, na época de Platão (c. 400 aC), cinco sólidos platônicos eram conhecidos. E quando Euclides escreveu seus Elementos (c. 300 g aC), um dos pilares deste trabalho era a prova da ausência de outros poliedros regulares. Essa prova é conhecida por dar o maior número de etapas dos axiomas euclidianos originais - 32.

Sólidos platônicos foram usados ​​para dados e ornamentos. Mas ele também recebeu um papel central no pensamento sobre a natureza - por exemplo, Platão sugeriu que, em certo sentido, tudo poderia consistir neles: terra de cubos, ar de octaedros, água de icosaedros, fogo de tetraedros e céu ("éter" ) dos dodecaedros.

E quanto aos outros poliedros? No século IV d.C. Papp de Alexandria escreveu que alguns séculos antes de Arquimedes descobrir 13 outros "poliedros regulares" - aparentemente, o que hoje é chamado de corpos arquimedianos - embora os detalhes disso estejam perdidos. E por mil anos, pouco aconteceu com os poliedros. Mas no século XV, com o início do Renascimento, os poliedros subitamente voltaram à moda. Leonardo da Vinci e Albrecht Dürer os usavam regularmente em arte e design, redescobrindo alguns dos corpos arquimedianos - e descobrindo novos poliedros, por exemplo, o icodosodecaedro.

Mas o maior passo adiante para o poliedro foi o trabalho de Johannes Kepler no início do século XVII. Tudo começou com uma teoria elegante, embora completamente incorreta. Kepler, com base em suposições teológicas, acreditava que o Universo deveria ser criado com precisão matemática e sugeriu que os seis planetas conhecidos na época se movessem ao longo de esferas aninhadas inscritas e descritas em torno de cinco sólidos platônicos:



Em seu livro de 1619, Harmonices mundi, Harmonia do Mundo, Kepler argumentou que muitas características da música, planetas e almas funcionam de acordo com princípios e relações geométricas semelhantes. Para confirmar os argumentos, Kepler estudou polígonos e poliedros, especialmente se interessando por objetos que compõem conjuntos completos, como sólidos platônicos.

Ele estudou o "poliedro de contato" com o qual pavimentar o avião - e encontrou, por exemplo, " azulejos monstruosos ", como ele os chamava (consistindo em pentágonos, pentagramas e decágonos). Ele estudou os "poliedros estrelados" e encontrou várias versões estreladas de sólidos platônicos (e corpo Kepler - Poinsot ). Em 1611, ele publicou um pequeno livro sobre a estrutura hexagonal dos flocos de neve, escrito como presente de ano para um de seus clientes. Neste livro, ele discutiu empacotamento tridimensional de esferas (e átomos esféricos), propondo a hipótese de que o empacotamento mais denso de bolas no espaço tridimensional (observamos regularmente sua implementação em pacotes de frutas nas lojas) é um empacotamento cúbico centrado na face (essa hipótese foi formalmente comprovada somente após 2000 anos - usando o Mathematica).

Em vários pacotes Kepler, diferentes poliedros estão ocultos. Vamos começar de qualquer esfera, pegar seus vizinhos e conectar seus centros para formar os vértices do poliedro. Na embalagem mais apertada de Kepler, outras 12 tocam em qualquer esfera e, a partir de seus centros, é obtido um cuboctaedro com 12 vértices e 14 faces. Mas Kepler também descreveu outro pacote, 8% menos denso, no qual cada esfera é coberta por outras 8 e outras 6 são muito próximas. Se conectarmos seus centros, obteremos um dodecaedro rômbico, com 14 vértices e 12 faces:



Tendo descoberto isso, Kepler começou a procurar outros "poliedros rômbicos". No dodecaedro rômbico que ele encontrou, os rombos consistiam em pares de triângulos equilaterais. Mas em 1619 Kepler também estudou losangos dourados - e encontrou um losango de trinta lados, após o qual pintou em seu livro sua bela imagem, ao lado do dodecaedro rômbico:



Kepler encontrou imediatamente uma aplicação para polígonos rômbicos: ele queria usá-los e um cubo para construir um modelo de esferas aninhadas adequadas para as órbitas das quatro luas de Júpiter, descobertas por Galileu em 1610.

Por que Kepler não abriu o hexaedro rômbico? Eu acho que ele chegou bem perto dele. Ele estudou poliedros estrelados não convexos. Ele olhou para o poliedro rômbico. Mas, aparentemente, por suas teorias astronômicas, bastava um rômbico de trinta lados, depois do qual ele parou de procurar.

Como resultado, é claro, as leis de Kepler, não relacionadas ao poliedro, tornaram-se a principal contribuição para a astronomia que sobreviveu a ela. Mas o trabalho de Kepler sobre o poliedro - embora realizado no âmbito de uma teoria física incorreta - permanece uma contribuição eterna para a matemática.

Nos três séculos seguintes, mais poliedros foram encontrados - e no início de XX os matemáticos já conheciam muitos de seus tipos:



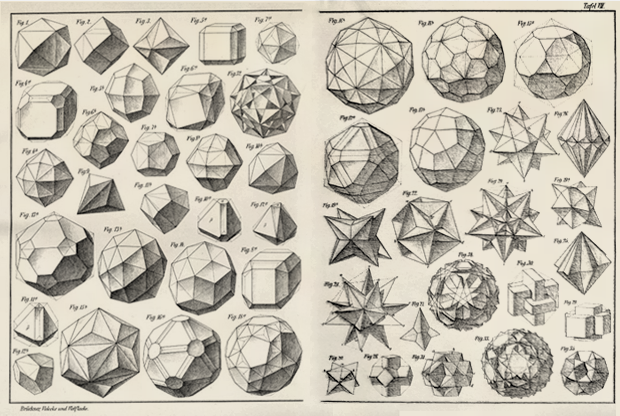
Mas, até onde eu sei, não havia RS entre eles. Sua descoberta aguardou o trabalho de Helmut Unkelbach . Nascido em 1910, defendeu seu doutorado em matemática na Universidade de Munique em 1937 (embora tenha estudado física pela primeira vez). Ele escreveu vários trabalhos sobre mapeamento conforme e - talvez devido ao estudo do mapeamento de poliedros - publicou em 1940 a obra "Poliedros simétricos de borda" em alemão.

Ele explicou que seu objetivo era um estudo abrangente de todos os poliedros possíveis que satisfazem uma nova definição especial de correção: todas as arestas têm o mesmo comprimento e estão no plano de simetria do poliedro. O principal resultado do trabalho foi uma tabela com 20 poliedros diferentes dessa propriedade:


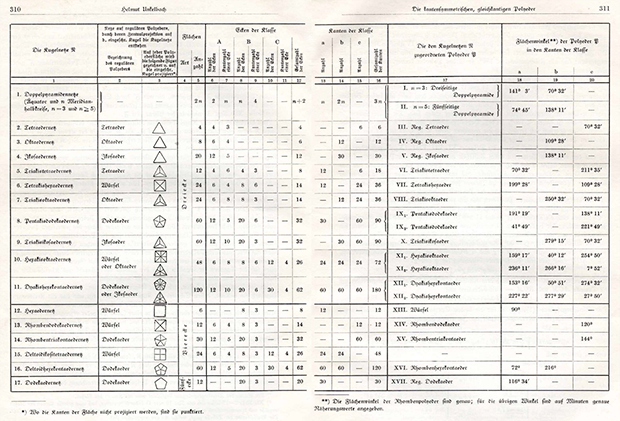Clicável

A maioria deles já era famosa. Mas Unkelbach destacou três deles que considerava novos: dois hexaciscosaedros (ou disdakis dodecahedron), dois hexacisicosahedra (ou disdacystriacontahedron) e o que ele chamou de Rhombenhexekontaeder, ou um hexaedro rômbico. E ele claramente considerou RSh sua principal conquista e incluiu uma fotografia de seu modelo feita por ele mesmo:



Como ele trouxe o RS? Ele começou com o dodecaedro e definiu dois de seus planos de simetria:



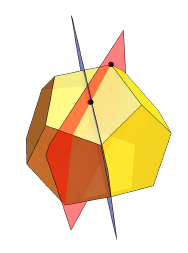
Em seguida, divida cada uma das suas faces:



Então, em essência, ele espremeu os centros de cada uma das faces por uma distância igual à distância usual do centro multiplicada por um certo α:



Para α <1, as faces resultantes não se cruzam. Mas para a maioria dos valores de α, seus lados não eram iguais. Isso acontece apenas em um determinado caso - quando o poliedro resultante coincide exatamente com o RS.

Unkelbach considerou seu trabalho de 1940 um “aquecimento” para um estudo mais extenso do “poliedro k-simétrico” com requisitos de simetria menos rigorosos. Mas, é claro, já era um milagre que, após o início da Segunda Guerra Mundial , um diário de matemática fosse publicado na Alemanha - logo após esta publicação, Unkelbach foi chamado à frente, onde desenvolveu torpedos acústicos para a frota alemã por vários anos.

Ele não publicou mais trabalhos sobre poliedros e morreu em 1968. Depois de anos, voltou ao mapeamento conforme e também começou a publicar sobre a teoria do voto , considerando-a a chave para criar uma democracia que funcionasse bem, e pensando que os matemáticos eram obrigados a fazer as pessoas começou a usá-lo.

Mas, mesmo aparecendo em um trabalho de 1940, o RS poderia ficar lá para sempre se em 1946 alguém Harold Scott MacDonald Coxeter não escrever uma breve resenha deste trabalho para a relativamente nova revista American Mathematical Reviews. Sua revisão lista os poliedros mencionados no trabalho, pois um naturalista pode listar novas espécies descobertas por ele em uma expedição. O principal é que ele descreveu lá o “notável hexaedro rômbico” e mencionou que “o formato de suas faces coincide com o formato das faces dos trinta lados, do qual é obtido dando uma forma de estrela”.

Poliedros não eram um tópico popular em matemática em meados do século XX, mas Coxeter era seu principal defensor - e estava de alguma forma conectado com todos que os estudavam. Em 1948, ele publicou o livro Os cientistas políticos certos. Descreve sistematicamente as diferentes famílias de poliedros regulares, em particular, e o grande triedro em forma de estrela - de fato, contendo o RS:



Mas em seu livro, Coxeter não menciona explicitamente o RS e, embora tenha sido homenageado com as referências de alguns amantes de poliedros, o RS continuou a ser pouco conhecido.

Quasicrystals

Os cristais sempre foram exemplos importantes de poliedros na natureza. Porém, no século XIX, quando a teoria atômica estava ganhando cada vez mais reconhecimento, os cientistas começaram a realizar pesquisas cada vez mais sérias no campo da cristalografia e na disposição dos átomos nos cristais. Os poliedros começaram a aparecer com freqüência, em particular, nas representações da geometria dos blocos repetidos de átomos (“células”) nos cristais.

Em 1850, já se sabia que só pode haver 14 dessas geometrias - entre elas também existe uma baseada no dodecaedro rômbico. Eles são notáveis ​​pela presença de simetrias de segunda, terceira, quarta ou sexta ordem - o que, em essência, é uma conseqüência do fato de que o espaço só pode ser preenchido com certos poliedros, assim como apenas polígonos regulares, como quadrados, podem preencher um plano bidimensional, triângulos e hexágonos.

E quanto a outros materiais não cristalinos - como líquidos ou vidro? Desde o início do século XX, as pessoas estão interessadas na possibilidade de presença de simetrias de quinta ordem pelo menos aproximadas. Não será possível preencher o espaço com os icosaedros corretos, mas pode ser possível criar seções de espaço de vinte lados com pequenas lacunas entre eles.

Essa questão permaneceu sem solução até a década de 1980, quando a cristalografia por difração de elétrons usando uma liga de alumínio e manganês de resfriamento rápido demonstrou a presença de simetria quíntupla. Já existiam teorias para alcançar tal simetria e, após alguns anos, também apareceram imagens feitas por um microscópio eletrônico, nas quais eram visíveis partículas com a forma de um triédrico rômbico:



E, enquanto as pessoas imaginavam como esses trinta-heptaedros poderiam ser combinados, um sixta-hexa rômbico apareceu - na forma de um "buraco" em um conjunto de 12 triedros rômbicos:



No começo, era chamada de estrela de 20 pontas. Porém, foi associado a descrições na literatura sobre o poliedro e identificado como RS.

Enquanto isso, a idéia de criar objetos a partir de elementos rômbicos ganhava cada vez mais popularidade. Michael Longe Higgins, oceanógrafo e especialista em formação de ondas oceânicas, ingressou no hobby em massa e, em 1987, patenteou um brinquedo baseado em elementos romboédricos, a partir dos quais foi possível montar uma "estrela Kepler" (RS) ou "bola Kepler" (meia rômbica). ):



E - embora eu só tenha descoberto agora - os blocos romboédricos, que consideramos em 2009 como uma opção para a criação de "Shipastiks", foram realmente produzidos pela empresa Dextro Mathematics Toys (Rhombo.com), que trabalhava na base da Longge-Higgins em San Diego

A questão de preencher com sucesso o espaço com figuras tridimensionais - ou mesmo um avião com figuras bidimensionais - é bastante complicada. Sabe-se desde a década de 1960 que, no caso geral, o problema de saber se um determinado conjunto de formulários pode preencher um plano é insolúvel. (Em princípio, é possível verificar se 1000 desses formulários podem ser compostos entre si, mas quanto mais formulários considerarmos, mais recursos de computação serão necessários).

Pessoas como Kepler provavelmente supunham que, se um conjunto de formas pudesse preencher um plano, isso poderia ser feito como um padrão repetitivo. No entanto, depois que ficou claro que, no caso geral, esse problema não foi resolvido, Roger Penrose, em 1974, apresentou dois formulários que podem preencher o avião sem repetir padrões. Em 1976, Penrose (e Robert Ammann) criaram uma versão simplificada dessas formas:



E sim, essas formas parecem losangos, embora não sejam ouro. Mas com ângulos de 36 °, 144 ° e 72 °, 108 °, eles têm simetria de 5 e 10 vezes.

Esses losangos não podem estabelecer padrões repetidos. Mas acontece que eles podem estabelecer um padrão construído de maneira sistemática e aninhada:



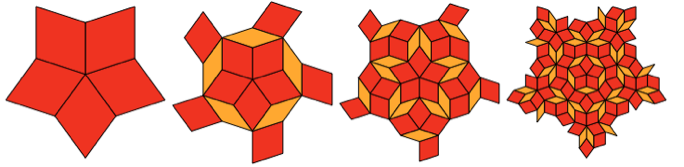
E sim, a parte do meio do terceiro passo é muito semelhante à Shipastik achatada. Mas isso não coincide completamente, os losangos externos têm um formato ligeiramente diferente.

No entanto, ainda existe uma conexão estreita entre eles. Imagine que começaremos não a partir de um avião, mas a partir de metade de um quadrado rômbico tridimensional de trinta quadrados, constituído por losangos dourados:



De cima, ele se parece exatamente com o início do design de mosaico Penrose aninhado. Se continuarmos esse processo, obtemos esse mosaico:



Se você olhar “de lado”, poderá ver que estes ainda são os mesmos losangos dourados:



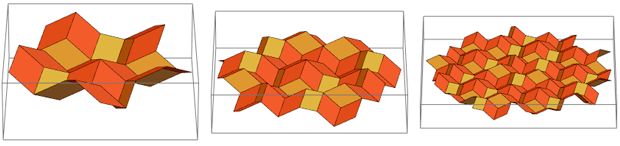
Depois de compilar quatro desses “telhados de Wieringa”, você pode obter apenas o RS:



Qual é a relação entre essas estruturas incorporadas e a maneira real de formar quase-cristais físicos? Ainda não está claro. Mas é bastante interessante ver como as sugestões de RS aparecem na natureza.

Historicamente, foi graças à discussão de quase-cristais que Sandor Kabaei começou a estudar RS usando o Mathematica, o que levou Eric Weinstein a descobri-los, o que levou à sua inclusão no Mathematica e na Wolfram Language, o que me levou a escolher um deles para o nosso logotipo. Em homenagem a isso, imprimimos um mosaico Penrose dentro do nosso Paper Shipastik:

Achatamento de espinho

Nosso Shipastik para Wolfram | Alpha estourou no mundo em 2009 com o lançamento do Wolfram | Alpha. Mas também temos o nosso Shipastik for Mathematica, que vem se desenvolvendo e evoluindo há muito tempo. Portanto, quando construímos nossa nova sede européia em 2011, dois Shipastiks competiram pela presença nela.

Nosso diretor de arte de longa data, Jeremy Davis, sugeriu o seguinte: pegue um dos Shipastiks e o "idealize" usando apenas seu "esqueleto". A decisão de começar com o RS foi simples. Mas então a aplainamos e, assim, a primeira versão do agora familiar logotipo apareceu:

Surpresa brasileira

Quando comecei este artigo, pensei que toda a história terminaria por aí. Afinal, eu já descrevi como escolhemos o RS para nós mesmos e como os matemáticos o criaram. Mas antes de terminar de escrever, decidi: "Examinarei todas as cartas sobre o Shipastik por todos os anos, apenas para garantir que não perdi nada".

E então eu notei um e-mail de junho de 2009 da artista brasileira Yolanda Kipriano. Ela escreveu que viu um artigo sobre Wolfram | Alpha em uma revista brasileira, chamou a atenção da Shipastika e forneceu um link para seu site. Mais de 9 anos se passaram desde então, mas eu ainda segui esse link e fiquei surpreso ao ver o seguinte:



Continuei lendo sua carta: “No Brasil, esse objeto se chama Giramundos ou a“ flor Mandakaru ”e é feito de guardanapos como um ornamento artístico”.

O que ?! No Brasil existe uma tradição associada ao Shipastik, e por todos os anos não ouvimos falar disso? Logo descobri suas imagens na rede. Uma pequena parte dos modelos era feita de papel, a maioria feita de tecido - mas havia muitos:



Escrevi para meu amigo brasileiro que trabalhou nas primeiras versões do Wolfram | Alpha. Ele respondeu rapidamente: “Esses objetos realmente parecem familiares. Para minha vergonha, não tinha o desejo de comparar duas e duas "e me enviou fotos do catálogo local de obras de arte:



A caçada começou: o que eram esses objetos e de onde eles vieram? Alguém da nossa empresa disse que sua bisavó do Chile fazia essas coisas em crochê, e sempre fazia um rabo para elas. Começamos a entrar em contato com pessoas que postavam fotos de "shipastiks folclóricos" na rede. Muitas vezes, eles compravam suas cópias nas lojas. Mas às vezes as pessoas diziam que sabiam como fazê-las. E todo mundo tinha quase a mesma história: eles aprenderam isso com as avós.

Uma maneira típica de coletar espigas populares - pelo menos em nosso tempo - é cortar 60 diamantes do papelão. Então todo mundo precisa ser enrolado em tecido e costurá-los:



Mas então surge um problema matemático imediatamente. Essas pessoas estão marcando e esculpindo losangos dourados corretamente com um ângulo de 63 °? Geralmente não. Eles fazem losangos a 60 ° a partir de pares de triângulos equilaterais - esta é a forma romboide padrão usada na fabricação de mantas. Então, como os Thornies acontecem? Bem, a diferença entre 60 ° e 63 ° é pequena e, se você costurar as faces, haverá espaço suficiente entre elas para a manobra, por isso é muito simples fazer um poliedro sem atingir ângulos absolutamente precisos. (Existem também quase Shipastiks, nos quais, como na construção de Unkelbach, em vez de faces, não há losangos, mas "triângulos externos" afiados).

Os picos na Internet são designados de maneira diferente. Na maioria das vezes - Giramundos. Muitas vezes, eles são chamados de Estrelas da Felicidade. O fato de que às vezes são chamadas de "estrelas da Morávia" é confuso, mas, na verdade, as estrelas da Morávia são poliedros muito mais nítidos (geralmente feitos de rhombocubooctahedron), que recentemente ganharam popularidade como luminárias.

Apesar de uma longa investigação, ainda não conheço toda a história dos picos populares. Aqui está o que eu descobri.Primeiro, a maioria dos picos populares hoje está concentrada no Brasil (embora tenhamos histórias sobre sua aparência em outros lugares). Em segundo lugar, a tradição parece bastante antiga, definitivamente apareceu muito antes do século XX e, talvez, vários séculos antes. Tanto quanto posso dizer, é passado de boca em boca, como é geralmente o caso da arte folclórica, e não encontrei nenhum documento histórico real sobre esse assunto.

A melhor informação foi fornecida por alguém Paula Guerra, que vendia espigões populares em um café turístico que ela administrava há dez anos, localizado na cidade histórica de São Luis do Paraiting. Ela disse que pessoas de todo o Brasil vieram ao seu café, viram picos populares e disseram algo como "eu não vejo essas coisas há cerca de 50 anos".

A própria Paula aprendeu sobre picos folclóricos (ela os chama de "estrelas") de uma mulher mais velha que morava em uma fazenda da família, que os fazia desde menina, e aprendeu isso com a mãe. Seu processo - aparentemente típico - consistia em juntar papelão em algum lugar (originalmente parecido com caixas de chapéu), cobrir as peças com pano e costurá-las para obter um objeto com cerca de 15 cm de tamanho.

Quantos anos tem um folk espetado? Isso só pode ser apreciado pela tradição oral. Encontramos várias pessoas que viram como os shipastiks eram feitos por seus parentes nascidos na área de 1900. Paula disse que dez anos atrás ela conheceu uma mulher de 80 anos que lhe disse que quando ela cresceu em uma fazenda de café há 200 anos, havia uma prateleira inteira onde havia espigas de gente feitas por quatro gerações de mulheres.

Parte da história da shipastik nacional parece girar em torno das tradições transmitidas de mãe para filha. Dizem que as mães costumavam fazer espinhos como presentes de casamento para suas filhas. Normalmente, os shipastiks eram feitos de restos de roupas e outras coisas que lembram as filhas sobre sua infância - algo como as colchas de retalhos hoje em dia para crianças que frequentam a faculdade.

No entanto, outra reviravolta foi descoberta com picos populares: muitas vezes antes de costurar em um brinquedo, a mãe colocava dinheiro que sua filha poderia usar em casos críticos. E a filha mantinha a shipastik junto com o material de costura, onde o marido dificilmente o encontraria. Alguns espinhos foram usados ​​como alfinetes de travesseiro - o que pode ter servido como um obstáculo adicional para os maridos.

Quais famílias apoiaram a tradição de fazer espigas populares? Desde cerca de 1750, existem muitas plantações de café e açúcar nas áreas rurais do Brasil, distantes das cidades. Até o século 20, os fazendeiros costumavam levar meninas para suas noivas - geralmente muito jovens, com até 13 anos - de cidades remotas. Talvez essas noivas - geralmente provenientes de boas famílias de descendência portuguesa, com uma educação relativamente boa - carregassem espinhos folclóricos.

Aparentemente, com o tempo, a tradição se espalhou para as famílias piores, e basicamente permaneceu lá. Mas em algum lugar no meio do século 20 - provavelmente quando as estradas começaram a aparecer no país, a urbanização começou e as pessoas começaram a deixar as fazendas - a tradição quase desapareceu. No entanto, nas escolas rurais do sul do Brasil na década de 1950, as meninas eram ensinadas em aulas de arte a fazer espigas folclóricas com um espaço especial para uso como cofrinhos.

Espigas de gente têm uma história diferente em diferentes partes do Brasil. Nas regiões fronteiriças meridionais (perto da Argentina e Uruguai) existe uma tradição segundo a qual “a estrela de São Miguel ”(ela também é uma expedidora nacional) foi feita nas aldeias por curandeiras (ou seja,“ bruxas ”) que, durante a fabricação de brinquedos, tiveram que pensar na saúde do paciente.

Em outras partes do Brasil, os brinquedos eram frequentemente chamados de nomes de flores e frutas que se assemelhavam ligeiramente a ela. No nordeste - Flor Mandacarú (com o nome das flores de cacto). Nas zonas húmidas tropicais - Carambola (em homenagem aos frutos da carambola, por vezes denominadas "estrelas tropicais"). Nas regiões arborizadas centrais - Pindaíva (em homenagem à fruta espetada vermelha).



Mas, na maioria das vezes, a popular shipastika é chamada Giramundo, uma palavra portuguesa bastante antiga que significa literalmente "mundo em turbilhão". Aparentemente, os brinquedos foram usados ​​como amuletos que trazem boa sorte com sua rotação ao vento. Caudas começaram a ser grudadas a eles recentemente, mas, aparentemente, era costume pendurá-las em casas, possivelmente nos feriados.

Muitas vezes, não está claro qual das tradições que deram origem à shipastika era original e quais apareceram recentemente. No desfile do Dia da Epifania (o nome local é “o dia dos três reis”) em São Luis do Paraiting, espinhos folclóricos foram usados ​​como símbolo da Estrela de Belém - mas isso, aparentemente, não é uma tradição muito antiga e claramente não mostra nenhuma conexão com religião.

Encontramos vários exemplos de picos folclóricos aparecendo em exposições de arte. Um deles, realizado em 1963, e dedicado à arte folclórica do nordeste do Brasil, foi organizado pela arquiteta Liina bo Bardi. A outra, onde o maior dos picos tridimensionais que eu já vi, foi exibida, foi organizada em 1997 pelo arquiteto e designer Vladavio Imperio:



Então, de onde vieram os espinhos populares? Ainda não sei disso. Eles poderiam aparecer no Brasil, poderiam vir de Portugal ou de outra parte da Europa. O fato de que peças de tecido e costura foram usadas para sua fabricação pode ser um argumento a favor de sua origem africana ou nativa americana.

Uma artesã moderna que fabrica shipastiks disse que sua bisavó - que fabricou esses brinquedos e nasceu no final do século 19 - vem de uma região da Itália chamada Romagna (e uma disse que aprendeu a fabricar shipastiks de sua avó, que era de canadenses franceses). Eu acho que é bem possível que espigas folclóricas já foram comuns na Europa, mas morreram há muitas gerações atrás, e essa tradição não sobreviveu lá. E, embora muitos poliedros diferentes apareçam nas pinturas européias dos séculos anteriores, não conheço nenhuma imagem do Shipastik entre eles (também não vi o Shipastik na arte islâmica).

Mas tenho certeza de que espigas populares têm um ponto de origem. Tal coisa dificilmente teria sido inventada duas vezes.

Devo dizer que esta não é a minha primeira caçada no campo da arte. A busca pelo primeiro padrão incorporado ( Sierpinski ) acabou sendo mais bem - sucedida - o que acabou me levando à cripta na igreja italiana, onde observei como esse padrão foi gradualmente descoberto usando um exemplo de mosaico de pedra do século XIII.

Até agora, a Shipastik não desistiu com tanta facilidade - e complica a situação é o fato de basicamente ser feito de tecido que não permanece tão bom quanto a pedra.

Picos ganham vida

Qualquer que seja sua origem, a Shipastik desempenha o papel de um logotipo forte e digno. Mas às vezes é divertido reviver o Shipastik - e, ao longo dos anos, criamos vários Shipastik personalizados por vários motivos:



ao usar o Wolfram | Alpha, o sistema geralmente exibe um Shipastik geométrico. Mas, às vezes, sua solicitação a anima - por exemplo, solicitações de π no dia do pi:

blog.stephenwolfram.com/data/uploads/2018/12/spikey-lives-happy-pi-day-video.mp4

Picos para sempre

Poliedros são eternos. Eles podem ser vistos na imagem de 500 anos atrás, que parece tão clara e moderna quanto o poliedro no meu computador.

Passei bastante tempo pesquisando coisas abstratas de computação (por exemplo, autômatos celulares). Eles também têm alguma atemporalidade. Mas para eles não encontrei nenhuma evidência histórica. Como objetos abstratos, eles podem ser criados a qualquer momento. Mas eles apareceram hoje graças às nossas plataformas e ferramentas conceituais - e ninguém as viu antes.

A rica história e constância dos poliedros têm milhares de anos. Na aparência, eles se parecem com pedras preciosas. Encontrar o certo tipo de poliedro é como encontrar uma gema em um universo geométrico de todas as formas possíveis.



O RS é uma dessas pedras surpreendentes e, estudando suas propriedades, comecei a apreciá-lo ainda mais. Mas também é uma jóia com uma história humana - e é muito interessante ver como uma abstração como um poliedro pode unir pessoas de todo o mundo com uma história e objetivos tão diferentes.

Quem foi o primeiro a inventar o hexaedro rômbico? Nós não sabemos, e talvez nunca saibamos. Mas agora que o temos, ele ficará conosco para sempre. Meu poliedro favorito.