Civilização da Primavera, 1/5

Parte 1. "Ku" dourado

Cerca de seis anos caí nas mãos do guia de um avô ^[50] em caminhões de meados do século XX. Sólido, impresso em livro raro de papel grosso e liso. A única coisa que resta na memória do meu avô após o colapso do país, guerras e viagens.



O livro de referência continha muitas características interessantes de desempenho, de modo que a palavra "capacidade de carga" se tornou familiar para mim desde a infância. E quando meu pai em uma caminhada mencionou que qualquer caminhão pesa tanto quanto é necessário, lembro-me disso. Lembrou-se e, muito mais tarde, interessou-se.

Pai estava certo. Para caminhões dos anos 60, essa regra é implementada com uma precisão bastante surpreendente:



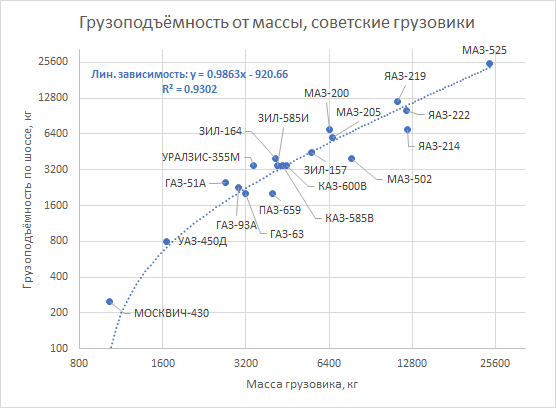
É muito mais curioso que esse padrão também seja observado para veículos que são completamente diferentes dos caminhões.

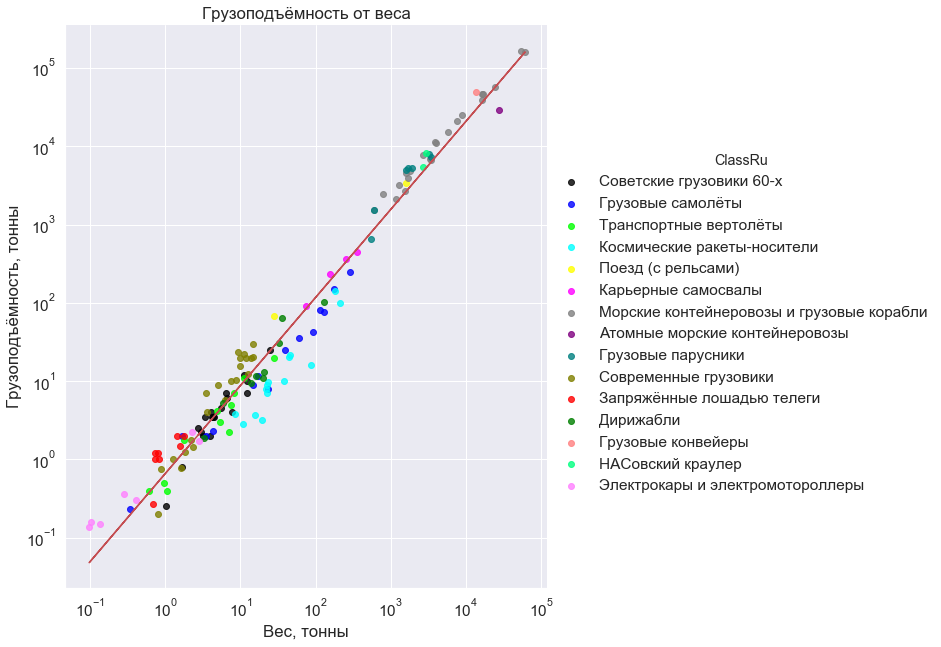
No começo, por diversão, coloquei aviões de carga no horário. E fiquei surpreso. Comecei a adicionar outros veículos. Cavalgar, flutuar e voar, construído nos séculos 19, 20 e 21, trabalhando com a energia térmica, atômica, eólica e até cavalo. Resultado? Potência fraca (indicador 1.125), se não apenas linear, dependência. Em massas de centenas de quilogramas a sessenta mil toneladas. Com os desvios, é claro, onde se poderia ir sem eles, até 10 vezes, às vezes, mas em seis ordens de massa isso é obviamente um pouco.

Aqui está essa dependência, espremendo-se na diagonal de um vasto campo vazio:


No gráfico observado: aeronaves de carga; helicópteros de transporte; aeronaves modernas e do início do século; veículos lançadores espaciais (em baixa órbita); Caminhões soviéticos dos anos 60; caminhões de mineração modernos; caminhões modernos da Rússia, EUA, China e Índia; carros elétricos e scooters; trens (com trilhos); navios contêineres nucleares; navios porta-contêineres e navios de carga (não navios-tanque); navios cargueiros de 17 a 20 séculos; correias transportadoras para transferência de minério; Trator Nassovsky para a exportação de mísseis para o início; e finalmente carrinhos puxados a cavalo.

Se você inserir o valor de Q , definido como a massa da carga transportada em relação à massa seca do veículo, eis a aparência de cada um dos grupos:



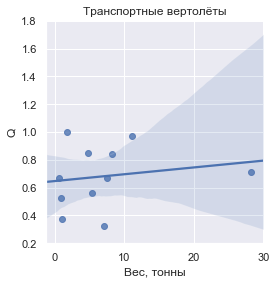
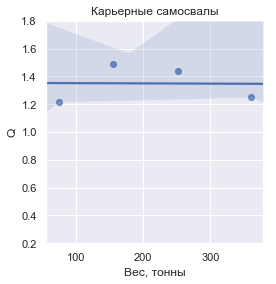
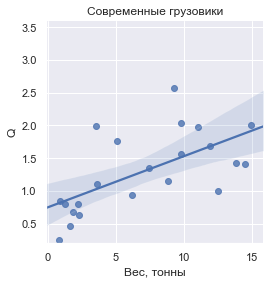
Em números, os valores Q são:

Classe de ativos	Q médio	Desvio padrão Q
Aviões de carga	0,667091	± 0,206162
Helicópteros de transporte	0,681605	± 0,225062
Aeronaves modernas e do início do século	0,842673	± 0,374622
Veículos lançadores espaciais (órbita baixa)	0,372446	± 0,155810
Caminhões soviéticos dos anos 60	0,777435	± 0,232425
Caminhões de mineração modernos	1.349610	± 0,136840
Caminhões modernos da Rússia, EUA, Índia, China	1,293679	± 0,604313
Cartões e scooters elétricos	1.098433	± 0,343791
Trem (com trilhos)	2.275989	± 0,205999
Navio de recipiente nuclear	1.035233	± NA
Navios porta-contêineres e cargueiros (não navios-tanque)	2.556004	± 0,378040
Veleiros de carga dos séculos 17-20	2.488461	± 0,671785
Correias transportadoras de carga	3,703704	± NA
Trator Nasovsky para o lançamento de mísseis	2,355919	± 0,525174
Carrinhos puxados a cavalo	1.203061	± 0,389183

Como pode ser visto, Q, embora nem todo lugar seja estritamente singular, mas dentro de cada grupo tende a um valor comum próximo à unidade.


Pareceu-me ... misterioso. Por que um veleiro de madeira, um carro elétrico de alumínio e um navio de contêiner atômico com capacidade para cem mil carros elétricos aumentam seu peso mais ou menos? O que nos faz criar veículos com qualidade Q ≈ 1 em massas diferentes milhares de vezes? Isso é uma manifestação das propriedades da física do mundo, a economia terrestre, é uma limitação da inteligência humana? Quão universal é essa lei, será implementada para civilizações de outras estrelas? Questões globais. É improvável que sejam resolvidos aqui e agora. Mas aqui é possível e necessário considerar e morder quanto isso resultará. É isso que faremos.

O recorde mundial ^{[ 180 ] de} levantar uma barra por uma pessoa de peso médio excede 200 kg. Teoricamente, isso significa que nosso corpo possui uma margem de segurança para cargas bruscas de pelo menos até Q = 2,5. No entanto, isso requer forças e treinamento exorbitantes que nunca são usados ​​nas atividades diárias. É mais aconselhável embalar o açúcar em sacos de 50 kg, embora isso exija quatro vezes mais carregadeiras ou andador. Note que esta situação é o resultado da evolução biológica, na qual o intelecto humano não participou (quase) e, portanto, possui um "álibi".

Física e engenharia por si só não proíbem altos Qs. Existe uma bomba turbo de hidrogênio para o mecanismo de vôo em andamento da Shuttle, aquela coisinha à direita na imagem que desenvolve 54 megawatts de potência ^{[ 60 ]} com um peso total de 350 kg:

[Crédito da imagem: [ 10 ]]

Se, simplificando, avalie Q por potência por quilograma de massa, isso é 100 vezes maior que o de um carro decente. Mas isso é quase como um foguete! É mais barato fabricar 100 carros com Q = 1 e transportar a carga com eles, em vez de tentar "aproveitar" essa unidade para um carrinho de rodas.

Tais considerações sugerem que as razões aqui são econômicas. Além disso, não no sentido restrito de economias e países específicos (porque nossos dispositivos são gerados por povos e sistemas muito diferentes), mas no sentido de "conveniência de esforços". A adequação é universal o suficiente para, aparentemente, aplicar-se a produtos muito diferentes e até a animais.

_{O artigo foi escrito para o site https://habr.com . Ao copiar, consulte a fonte. O autor do artigo é Evgeny Bobukh .}

Vamos tentar investigar os limites dessa conveniência quantitativamente. Colocamos a pergunta: como o custo de um dispositivo de massa fixa depende de Q ? Aqui, por exemplo, existe um caminhão basculante de 10 toneladas, que leva 10 toneladas de carga. Também queremos produzir 10 toneladas, mas tirando 20 toneladas ( Q = 2) ou até 50 ( Q = 5). No mesmo nível de desenvolvimento de tecnologia, o mesmo volume de produção. É claro que cargas mais altas aumentarão os requisitos para materiais (aço -> titânio?), E para motores (outras temperaturas, pressões) e engenharia (menos tolerâncias a erros, projetos mais complicados). Claramente, à medida que o Q cresce, tudo ficará mais caro. Mas quantas vezes, comparado com as dez toneladas?

Essa tarefa, é claro, não é trivial. No entanto, algumas estimativas para isso podem ser obtidas a partir das considerações mais gerais. O que faremos agora.

Introduzimos a função C ( Q ). Ele descreve o menor custo possível de um dispositivo com eficiência Q , expresso nos custos de um dispositivo similar com a mesma massa em Q = 1. O que se sabe sobre ele?

1. C (1) = 1, por definição.

2. C ( Q ) é uma função contínua, pelo menos até que a diferença de massa seja medida pelos átomos das peças. Intuitivamente, parece suave o suficiente para ter os primeiros derivados. Acho que podemos admitir (como na maioria das funções físicas) que geralmente é analítico.

3. C ( Q ) é uma função estritamente crescente. Quanto maior a qualidade de Q , mais difícil é tornar a estrutura e mais caro é. I.e. dC ( Q ) / dQ > 0 pelo menos para Q > 0.

4. Com Q maior que cerca de 3, C ( Q ) começa a aumentar mais rapidamente do que linearmente. Porque Como vemos que é mais barato para as pessoas fabricar três caminhões por dez toneladas com Q = 1 do que um para trinta com Q = 3. Resumindo, escrevemos: k * C (1) < C ( k ) para k > ≈3 - outro em palavras, C ( k ) cresce mais rápido que k , para k > ≈3.

5. Da mesma forma, uma vez que dez aeronaves com Q = 0,1 são claramente antieconômicas que uma com Q = 1 (porque constroem a segunda, não a primeira), para k > ≈3, temos: k * C (1 / k )> C (1), ou C (1 / k )> 1 / k .

6. O custo da bomba do Shuttle sugere que pelo menos até Q ~ 100 o valor de C ( Q ) não aumenta como um expoente com um indicador significativo. Caso contrário, esse TNA não custaria milhões de dólares, mas algum tipo de US $ 10 ²⁰ , e dificilmente teríamos conseguido. I.e. C (100) é algo em torno de 10 ³ - 10 ⁸ , mas não 10 - ¹⁵ .

7. O que é C (0) igual? Esse é o custo do dispositivo, que ainda pode se mover, mas é incapaz de retirar qualquer carga. Obviamente, esse "caminhão" é mais barato que um caminhão cheio. Mas quantas vezes? A história mostra isso às vezes, em vez de dezenas ou centenas. Cerca de 15 anos se passaram desde a primeira aeronave capaz de se mover apenas ( Q = 0) para o transporte aéreo de mercadorias, desde os primeiros carros a gasolina até caminhões bastante decentes com Q = 1,5 ([ 120 ] + [ 130 ]), um pouco mais. Se esse desenvolvimento fosse de uma complexidade incrível, dificilmente seria concluído tão rapidamente. Consequentemente, a dificuldade de fabricar e o custo de um veículo com Q = 0 não devem ser radicalmente diferentes dos de Q = 1. Portanto, esperamos que C ( 0 ) esteja em torno de 0,1 - 0,5.

8. Esta função faz sentido para Q negativo? Bastante! Um caminhão com Q = -0,5 é aquele que só se moverá se você remover metade de seu peso de um guindaste de torre. E Q = -1 - este é um carrinho que desenvolve tração zero. Capaz de transportar carga somente se você a levar a reboque. Ou seja, geralmente sem um motor. Obviamente, seu custo, se não diferente de zero, é muito pequeno. Portanto, coloque C (-1) ≈ 0.

9. E o que é C (-2)? Esse é o custo de um dispositivo que precisa ser levantado com pelo menos o dobro do seu peso para se mover! Sim, as áreas Q <-1 são âncoras, fundações, estacas, freios. Dispositivos que impedem o movimento. Existe, é claro, uma dinâmica completamente diferente e suas próprias leis, mas pelo menos vemos que C ( Q ) não termina com uma singularidade em Q <-1, e que na região Q = -1 ela tem um mínimo e, portanto, pelo menos Uma pequena vizinhança deste ponto C ( Q ) deve se comportar como uma parábola.

Assim, C ( Q ) esboçado se parece com isso:


Expandimos C ( Q ) em uma série de Taylor no ponto Q = -1:



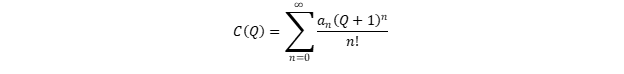
Da propriedade (8) decorre que ₀ = 0. As propriedades (4), (5) e parcialmente (9) sugerem que um _{1 é} próximo de zero ou, em qualquer caso, que sua contribuição não domina no intervalo 0. .3

E então verifica-se que o primeiro termo diferente de zero na expansão de C ( Q ) é parabólico e que com Q na região das unidades C ( Q ) se comporta aproximadamente como uma função quadrática ou um pouco mais rápida:

C ( Q ) ≈ a ₂ * ( Q +1) 2/2 + O (( Q + 1 ) ³ )

E de [1] segue-se que ₂ ≈ 1/2.

Finalmente, como pelo menos até Q ~ 100 a função C ( Q ) ainda não é exponencial (propriedade (6)), podemos colocá-la lá igual a Q ^p com o expoente p em algum lugar na região de 2 ... 4. Dificilmente mais.

Conclusão: Para uma massa fixa, o custo do dispositivo C (Q) não aumenta mais fraco que (Q + 1) 2/4, mas não é mais rápido do que cerca de O (Q ⁴ ) [1]

É possível olhar para a real dependência de C ( Q ) para entender como essa conclusão é correta? É dificil A maioria dos mecanismos criados pelo homem são massas diferentes, mas Q fixo na região da unidade. Precisamos do oposto: aproximadamente a mesma massa, mas Q diferente. No começo, eu esperava dados sobre motores de aeronaves ... mas o trabalho ^{[ 70 ] [ 80 ]} em seus preços é muito engraçado. Os preços dos motores são classificados lá, e apenas as fórmulas para previsão e erros médios são publicadas.

Felizmente, a ajuda veio dos carros ^{[ 150 ]} . É com eles, com aproximadamente a mesma massa, que são encontrados motores de várias capacidades. E embora a energia ainda não seja uma carga transportável, com algum esforço de engenharia é aproximadamente proporcional a ela. O que nos permite estimar se nossa fórmula está próxima da realidade.

Parece que sim:

[Fonte: [ 150 ]]

Pontos azuis são carros reais. Numa primeira aproximação, seu preço aumenta como densidade de potência no grau de 2,3.

Pontos vermelhos - o preço calculado pela fórmula [1], com base no pressuposto de que Q = 1 corresponde aos carros mais baratos por quilograma na faixa de US $ 20 a 30 mil. Pode-se ver que a fórmula realmente fornece uma boa estimativa de C ( Q ) a partir de baixo (para onde pretendemos).

Ao olhar para a massa desses pontos saborosos, há uma forte tentação: desenhar C ( Q ) através deles e, assim, examinar diretamente a dependência. Isso não pode ser feito. Principalmente porque o preço de um carro de passeio é determinado não apenas por suas características de tração. É difícil imaginar um carro de cem kilobaxes que não possua o melhor ar-condicionado, os assentos mais confortáveis ​​e o "cinzeiro de platina com moldura banhada a ródio". E tudo isso custa dinheiro que não tem nada a ver com o nosso C ( Q ). No entanto, aqui o "ramo" inferior dos carros, passando quase exatamente de acordo com o C ( Q ) calculado, parece interessante. Atrevo-me a admitir que estes são apenas carros sem frescuras. Onde "não damas, mas para ir". Mas mais de US $ 100 mil para um carro, eles não estão mais lá.

_{O artigo foi escrito para o site https://habr.com . Ao copiar, consulte a fonte. O autor do artigo é Evgeny Bobukh .}

Assim, somos capazes de estimar o custo de dispositivos com Q alto, pelo menos em ordem de magnitude. Por que isso foi necessário?

Mas porque Dê uma olhada no primeiro passo do transportador espacial. Bem, pelo menos Proton-M ^{[ 110 ]} , para concretude. Ela é um veículo quase completo, com motores, um sistema de controle, uma margem de segurança decente e um peso seco de 31 toneladas. Ao mesmo tempo, no início do foguete, ele arrasta não apenas a carga, mas também todo o combustível, todos os estágios superiores e, é claro, ele próprio. No total - 683 toneladas. Além de sobrecarga inicial, total (efetivo) 1068 toneladas de carga! Do ponto de vista do primeiro estágio, ele funciona em um modo terrível Q = (1068/31) = 34,4! Isso equivale a 50 toneladas de carga empilhadas em um carro de passageiro.

E sabemos que o custo de um dispositivo com Q alto é pelo menos (Q + 1) 2/4 vezes maior do que algo semelhante com Q ≈ 1. Para Proton, isso equivale a ... 313 vezes.

Ou seja, o Proton deve custar 300 vezes mais que um dispositivo similar com Q = 1. E esse número depende pouco do progresso e da tecnologia. Assim que os "cientistas britânicos" inventam uma super liga que torna um foguete mais barato, os motores terrestres também ficam mais baratos. Portanto, um foguete químico, mesmo reutilizável, sempre será muito caro. Goste ou não.

Bom Digamos 300 vezes. Mas comparado com o que ? Seria bom comparar nossos cálculos com alguns dispositivos objetivamente existentes para eliminar erros graves?

Infelizmente, não há mísseis de trinta toneladas com Q = 1. Mas existem análogos aproximados adequados para comparação:

• O primeiro é um caminhão de mineração. Sim, não um foguete. Mas, ainda assim, é também um motor térmico, não uma engenharia inteiramente trivial, e um dos meios mais baratos para o transporte de mercadorias. E se já estamos falando sobre exploração espacial, o caminhão não deveria ser o protótipo do modelo de negócios da cabine espacial? Então, vamos tentar, pelo menos para uma estimativa geral. Aqui está uma Belaz-7540 de 30 toneladas. O preço de mercado ^{[ 140 ]} é de 3,7 milhões de rublos, ou seja, $ 62K. Para Proton, isso é convertido no custo do primeiro estágio na região de US $ 19 milhões. Wikipedia significa ^{[ 100 ]} custo inicial como US $ 65 milhões. Bem próximo, já que esse valor inclui muito mais, exceto pelo preço do primeiro passo.
• Em [ 160 ] é descrita uma plataforma experimental de foguetes sobre trilhos. Uma massa de 10 toneladas, cinco etapas, acelera para 4 km / s. O preço é 750 kilobax. A julgar pelas imagens e parâmetros publicados, este dispositivo funciona em algum lugar com Q = 10. Não é uma unidade, mas ainda não 34. Se você começar com esses números, o primeiro passo do Proton deve custar algo em torno de US $ 23 milhões.
• Em geral, quando tento imaginar um foguete com Q = 1, na minha mente há uma espécie de espaço em branco robusto com um pequeno entalhe cheio de pólvora. A pólvora queima e empurra o branco para a frente. Um pouco, você não vai acelerar muito. Procrastinei essa foto por dois dias, até perceber que ela me lembra. Isto é ... um martelo pneumático! Onde o gás se expande e empurra o espaço em branco. A bastardização final da idéia de um motor a jato, ainda preservando algum tipo de parentesco. Bem, nós estamos olhando. Sim, aqui está o martelo pneumático ^{[ 170 ]} Stanko M212. O peso do disco é de 2 toneladas, toda a estrutura é de 58,3 toneladas. O sistema Q , portanto, é um modesto 0,034. Vendido por 40 mil euros. Se extrapolarmos o custo dessa piada para Q = 34,4, de acordo com a fórmula [1], obteremos ... 47 milhões de euros. Ou 24 milhões em proporção acima de 30 toneladas.

Parece que não estamos realmente divorciados da realidade.

Para resumir. Como os foguetes, mesmo os reutilizáveis, são de 2 a 3 pedidos de magnitude mais caros que os caminhões, qualquer assentamento espacial feito de materiais terrestres também custará 100-1000 vezes mais caro que um equivalente terrestre. Essa é uma barreira muito alta ao desenvolvimento.

Os mísseis são caros porque são muito pesados ​​e são forçados a trabalhar quando não são saudáveis ​​com alta Q. Mas por que os foguetes são pesados? A resposta (que é um pouco mais profunda que a fórmula de Tsiolkovsky) será considerada na segunda parte.

Para ser continuado .

Atualização: várias pessoas tentaram apontar as ambigüidades em relação ao combustível ao considerar os mísseis. Eu pensei sobre isso. E percebi que realmente há alguma imprecisão no artigo. Visto nos comentários aqui .