Estimativa da orientação espacial ou Como não ter medo dos filtros Mahoney e Majwik

Do que estamos falando?

A aparição em Habre de um post sobre o filtro Majwik foi um evento simbólico à sua maneira. Aparentemente, o entusiasmo geral pelos drones reviveu o interesse na tarefa de avaliar a orientação do corpo por medições inerciais. Ao mesmo tempo, os métodos tradicionais baseados no filtro Kalman deixaram de satisfazer o público - por causa dos altos requisitos de recursos de computação que eram inaceitáveis ​​para drones ou por causa das configurações complexas e não intuitivas.

A postagem foi acompanhada por uma implementação muito compacta e eficiente do filtro em C. No entanto, a julgar pelos comentários, o significado físico desse código, bem como de todo o artigo, permaneceu vago para alguém. Bem, admitimos honestamente: o filtro Majwik é o mais complexo do grupo de filtros, baseado em geral em princípios muito simples e elegantes. Vou considerar esses princípios no meu post. O código não estará aqui. Meu post não é uma história sobre uma implementação específica do algoritmo de estimativa de orientação, mas um convite para inventar suas próprias variações em um determinado tópico, o que pode ser muito.

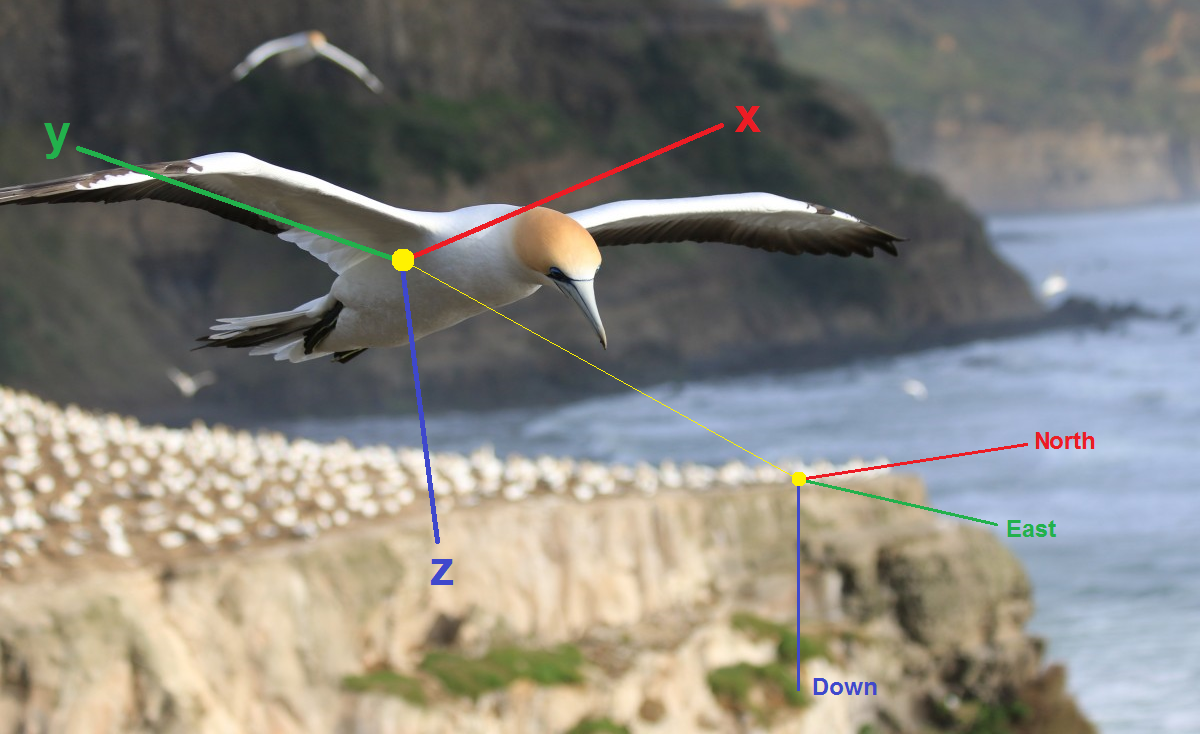
Vista de orientação

Lembre-se do básico. Para avaliar a orientação do corpo no espaço, primeiro é necessário selecionar alguns parâmetros que juntos determinam exclusivamente essa orientação, ou seja, essencialmente a orientação do sistema de coordenadas associado $$$xyz$ sistema relativamente condicionalmente fixo - por exemplo, o sistema geográfico NED (norte, leste, baixo). Então você precisa fazer equações cinemáticas, ou seja, expressam a taxa de alteração desses parâmetros através da velocidade angular dos giroscópios. Finalmente, é necessário introduzir medidas vetoriais de acelerômetros, magnetômetros etc. no cálculo. Aqui estão as maneiras mais comuns de representar orientação:

Ângulos de Euler - rolo (rolo, $$$\ phi$ ), pitch (pitch, $$$\ theta$ ), curso (cabeçalho, $$$\ psi$ ) Este é o conjunto de parâmetros de orientação mais intuitivo e conciso: o número de parâmetros é exatamente igual ao número de graus de liberdade rotacionais. Para esses ângulos, podemos escrever as equações cinemáticas de Euler . Eles gostam muito de mecânica teórica, mas em problemas de navegação são de pouca utilidade. Primeiramente, conhecer os ângulos não permite converter diretamente os componentes de qualquer vetor de um sistema de coordenadas geográficas conectado a um sistema ou vice-versa. Em segundo lugar, em um passo de ± 90 graus, as equações cinemáticas degeneram, o rolo e o curso se tornam indefinidos.

Matriz de Rotação - Matriz $$$\ mathbf {C}$ Tamanho 3 × 3, pelo qual é necessário multiplicar qualquer vetor no sistema de coordenadas associado para obter o mesmo vetor no sistema geográfico: $$$\ mathbf {r} _ {NED} = \ mathbf {C} \ mathbf {r} _ {xyz}$ . A matriz é sempre ortogonal, ou seja, $$$\ mathbf {C} = \ mathbf {C} ^ {T}$ . A equação cinemática para ela tem a forma $$$\ ponto {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega}$ .
Aqui $$$\ mathbf {\ Omega}$ - uma matriz de componentes de velocidade angular medidos por giroscópios em um sistema de coordenadas conectado:

$$

$$\ mathbf {\ Omega} = \ begin {bmatrix} 0 & - \ omega_ {z} & \ omega_ {y} \\ \ omega_ {z} & 0 & - \ omega_ {x} \\ - \ omega_ {y } & \ omega_ {x} & 0 \\ \ end {bmatrix}$$

A matriz de rotação é um pouco menos óbvia que os ângulos de Euler, mas, diferentemente deles, permite converter diretamente vetores e não perde significado em nenhuma posição angular. Do ponto de vista computacional, sua principal desvantagem é a redundância: por três graus de liberdade, nove parâmetros são introduzidos ao mesmo tempo e todos precisam ser atualizados de acordo com a equação cinemática. O problema pode ser ligeiramente simplificado usando a ortogonalidade da matriz.

O quaternion de rotação é um remédio radical, mas muito pouco intuitivo, contra redundância e degeneração. Este é um objeto de quatro componentes. $$$\ mathbf {q} = q_ {0} + q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ - nem um número, nem um vetor e nem uma matriz. O quaternion pode ser visto de dois ângulos. Primeiro, que tal a quantidade formal de escalar $$$q_ {0}$ e vetor $$$q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ onde $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ - vetores de eixo unitário (que, é claro, parece absurdo). Em segundo lugar, como uma generalização de números complexos, onde agora usamos não um, mas três unidades imaginárias diferentes $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ (o que não soa menos absurdo). Como um quaternion está relacionado a uma virada? Através do teorema de Euler: um corpo sempre pode ser transferido de uma determinada orientação para outra com uma rotação finita em algum ângulo $$$\ alpha$ em torno de algum eixo com um vetor de guia $$$\ mathbf {u}$ . Estes ângulo e eixo podem ser combinados em um quaternion: $$$\ mathbf {q} = \ mathrm {cos} (\ alpha / 2) + \ mathbf {u} \ mathrm {sin} (\ alpha / 2)$ . Como uma matriz, um quaternion pode ser usado para converter diretamente qualquer vetor de um sistema de coordenadas para outro: $$$\ mathbf {r} _ {NED} = \ mathbf {q} \ mathbf {r} _ {xyz} {\ mathbf {q}} ^ {- 1}$ . Como você pode ver, a representação de orientação do quaternion também sofre redundância, mas muito menos que a matriz: um parâmetro extra é apenas um. A revisão abrangente dos quaternions já estava em Habré . Eles conversaram sobre geometria e gráficos 3D. Também estamos interessados ​​em cinemática, uma vez que a taxa de mudança do quaternion deve estar relacionada à velocidade angular medida. A equação cinemática correspondente tem a forma $$$\ ponto {\ mathbf {q}} = 1/2 \ mathbf {q} \ mathbf {\ omega}$ onde está o vetor $$$\ mathbf {\ omega}$ também considerado um quaternion com uma parte escalar zero.

Esquemas de filtro

A abordagem mais ingênua para calcular a orientação é armar-se com uma equação cinemática e atualizar de acordo com ela qualquer conjunto de parâmetros de que gostamos. Por exemplo, se escolhermos uma matriz de rotação, podemos escrever um ciclo com algo no espírito de C += * Omega * dt . O resultado vai decepcionar. Os giroscópios, especialmente os MEMS, têm compensações de zero grandes e instáveis ​​- como resultado, mesmo em repouso completo, a orientação calculada terá um erro acumulado ilimitado (desvio). Todos os truques inventados por Mahoney, Majwick e muitos outros, sem me excluir, visavam compensar essa deriva, envolvendo medições de acelerômetros, magnetômetros, receptores GNSS, defasagens, etc. Assim, toda uma família de filtros de orientação nasceu, com base em um princípio básico simples.

Princípio básico. Para compensar o desvio da orientação, é necessário adicionar à velocidade angular medida pelos giroscópios uma velocidade angular de controle adicional construída com base nas medições vetoriais de outros sensores. O vetor de velocidade angular de controle deve se esforçar para combinar as direções dos vetores medidos com suas direções verdadeiras conhecidas.

Uma abordagem completamente diferente é adotada aqui do que na construção do termo de correção do filtro Kalman. A principal diferença é que a velocidade angular de controle não é um termo, mas um fator para o valor estimado (matriz ou quaternião). Seguem-se vantagens importantes:

• Um filtro de avaliação pode ser construído para a orientação em si, e não para pequenos desvios da orientação em relação aos fornecidos pelos giroscópios. Além disso, os valores estimados atenderão automaticamente a todos os requisitos que a tarefa impõe: a matriz será ortogonal, o quaternião normalizado.
• O significado físico da velocidade angular de controle é muito mais claro que o termo de correção no filtro Kalman. Todas as manipulações são feitas com vetores e matrizes no espaço físico tridimensional comum e não em um espaço de estado multidimensional abstrato. Isso simplifica bastante o refinamento e o ajuste do filtro e, como bônus, permite que você se livre de matrizes de grande dimensão e bibliotecas de matrizes pesadas.

Agora vamos ver como essa ideia é implementada em opções de filtro específicas.

Filtro Mahoney. Toda a matemática furiosa do artigo original de Mahoney foi escrita para justificar equações simples (32). Nós os reescrevemos em nossa notação. Se ignorarmos a estimativa dos deslocamentos nulos dos giroscópios, restam duas equações principais - a equação cinemática da própria matriz de rotação (com a velocidade angular de controle na forma de uma matriz) $$$\ mathbf {\ Omega} '$ ) e a lei da formação dessa mesma velocidade na forma de um vetor $$$\ mathbf {\ omega} '$ . Para simplificar, assumimos que não há acelerações ou captadores magnéticos e, graças a isso, as medidas de aceleração de queda livre estão disponíveis para nós. $$$- \ hat {\ mathbf {g}} _ {xyz}$ dos acelerômetros e do campo magnético da Terra $$$\ hat {\ mathbf {m}} _ {xyz}$ de magnetômetros. Ambos os vetores são medidos por sensores em um sistema de coordenadas conectado e no sistema geográfico sua posição é conhecida: $$$- \ mathbf {g} _ {NED}$ apontando para cima $$$\ mathbf {m} _ {NED}$ - para o norte magnético. Em seguida, as equações do filtro Mahoney terão a seguinte aparência:

$$

$$\ ponto {\ mathbf {C}} = \ mathbf {C} (\ mathbf {\ Omega} + \ mathbf {\ Omega} ') \\ \ mathbf {\ omega'} = k_ {g} \ hat {\ mathbf {g}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {g} _ {NED} + k_ {m} \ hat {\ mathbf {m}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {m} _ {NED}$$

Vamos olhar com cuidado para a segunda equação. O primeiro termo no lado direito é um produto vetorial. O primeiro fator é a aceleração medida da gravidade, o segundo é verdadeiro. Como os fatores devem estar em um sistema de coordenadas, o segundo fator é convertido em um sistema conectado pela multiplicação por $$$\ mathbf {C} ^ {T}$ . A velocidade angular, construída como um produto vetorial, é perpendicular ao plano dos vetores fatoriais. Ele permite que você gire a posição estimada do sistema de coordenadas associado até que os vetores de fatores coincidam na direção - o produto vetorial será redefinido para zero e a rotação será interrompida. Coeficiente $$$k_ {g}$ define a rigidez de tal feedback. O segundo termo executa uma operação semelhante com um vetor magnético. De fato, o filtro Mahoney incorpora a tese conhecida: o conhecimento de dois vetores não colineares em dois sistemas de coordenadas diferentes permite restaurar exclusivamente a orientação mútua desses sistemas. Se houver mais de dois vetores, isso fornecerá redundância de medição útil. Se houver apenas um vetor, um grau de liberdade rotacional (movimento em torno desse vetor) não poderá ser corrigido. Por exemplo, se apenas um vetor for fornecido $$$- \ mathbf {g}$ , então você pode ajustar o desvio da rotação e da inclinação, mas não o curso.

Obviamente, o filtro Mahoney não precisa usar uma matriz de rotação. Existem também variantes de quaternion não-canônicas.

Plataforma de giroscópio virtual. No filtro Mahoney, aplicamos a velocidade angular de controle $$$\ mathbf {\ omega '}$ ao sistema de coordenadas associado. Mas você pode aplicá-lo à posição estimada do sistema de coordenadas geográficas. A equação cinemática assume a forma

$$

$$\ ponto {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega} - \ mathbf {\ Omega} '\ mathbf {C}$$

Acontece que essa abordagem abre caminho para analogias físicas muito frutíferas. Basta lembrar com o que a técnica giroscópica começou - os sistemas de navegação vertical e inercial baseados em uma plataforma estabilizada com giroscópios em um cardan.


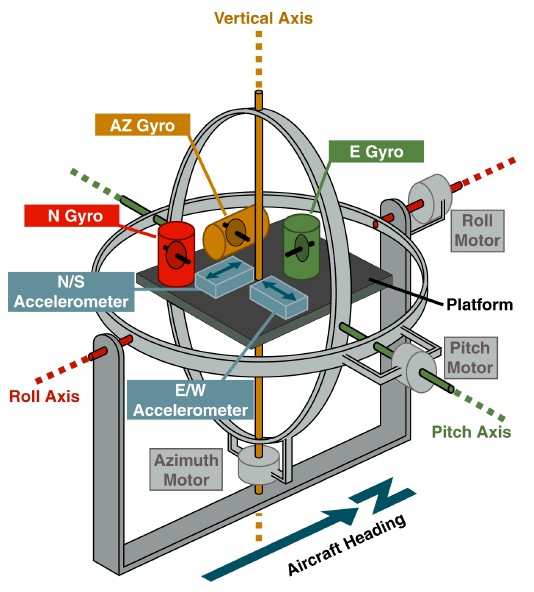www.theairlinepilots.com

O objetivo da plataforma foi a materialização do sistema de coordenadas geográficas. A orientação do transportador foi medida em relação a esta plataforma por sensores de ângulo nos quadros de suspensão. Se os giroscópios tiveram uma deriva, a plataforma também se desviou deles e foram acumulados erros nas leituras dos sensores de ângulo. Para eliminar esses erros, foi introduzido feedback dos acelerômetros instalados na plataforma. Por exemplo, o desvio da plataforma em relação ao horizonte em torno do eixo norte foi percebido pelo acelerômetro do eixo leste. Este sinal permitiu definir a velocidade angular de controle $$$\ mathbf {\ omega '}$ retornando a plataforma ao horizonte.

Podemos usar os mesmos conceitos visuais em nossa tarefa. A equação cinemática descrita deve então ser lida da seguinte forma: a taxa de mudança na orientação é a diferença entre dois movimentos rotacionais - o movimento absoluto da transportadora (o primeiro termo) e o movimento absoluto da plataforma giroscópica virtual (o segundo termo). A analogia pode ser estendida à lei da formação da velocidade angular de controle. Vetor $$$- \ hat {\ mathbf {g}} _ {NED} = - \ mathbf {C} \ hat {\ mathbf {g}} _ {xyz}$ Representa o testemunho de acelerômetros, supostamente em pé em uma plataforma de giroscópio. Então, por razões físicas, você pode escrever:

$$

$$\ omega '_ {N} = - gk_ {g} \ hat {g} _ {E}, \; \ omega '_ {E} = gk_ {g} \ hat {g} _ {N}$$

Seria possível chegar exatamente ao mesmo resultado de maneira formal, através da multiplicação de vetores no espírito do filtro Mahoney, mas agora não em um sistema conectado, mas em um sistema de coordenadas geográficas. Isso é apenas necessário?

A primeira dica de uma analogia útil entre a plataforma e a navegação inercial com amarração aparece, aparentemente, na antiga patente da Boeing . Então essa idéia foi ativamente desenvolvida por Salychev e, recentemente, por mim também . As vantagens óbvias dessa abordagem:

• A velocidade angular de controle pode ser formada com base em princípios físicos compreensíveis.
• Naturalmente, os canais horizontal e direcional, que são muito diferentes em suas propriedades e métodos de correção, são separados. No filtro Mahoney eles são misturados.
• É conveniente compensar o efeito das acelerações devido ao uso de dados GNSS, emitidos precisamente em eixos geográficos, e não relacionados.
• É fácil generalizar o algoritmo para o caso de navegação inercial de alta precisão, onde é necessário levar em consideração a forma e a rotação da Terra. Como fazer isso no esquema Mahoney, não consigo imaginar.

Filtro de Majwick. Majwik escolheu o caminho mais difícil . Se Mahoney, aparentemente, intuitivamente tomou sua decisão e a justificou matematicamente, Majwik, desde o início, provou ser um formalista. Ele se comprometeu a resolver o problema de otimização. Ele argumentou assim. Defina a orientação do quaternion de rotação. No caso ideal, a direção calculada de algum vetor medido (deixe-nos $$$- \ mathbf {g}$ ) coincide com o verdadeiro. Então será $$${\ mathbf {q}} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q} = \ hat {\ mathbf {g}} _ {xyz}$ . Na realidade, isso nem sempre é possível (especialmente se houver mais de dois vetores), mas você pode tentar minimizar o desvio $$$\ mathbf {F} = {\ mathbf {q} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q}} - \ hat {\ mathbf {g}} _ {xyz}$ da igualdade exata. Para isso, introduzimos o critério de minimização

$$

$$E = \ frac {1} {2} | \ mathbf {F} | ^ {2} \ rightarrow \ mathrm {min}$$

A minimização requer uma descida do gradiente - movendo-se em pequenos passos na direção oposta ao gradiente $$$\ nabla E$ , ou seja, oposto ao aumento mais rápido da função $$$E$ . Aliás, Majwik comete um erro: em todas as suas obras ele não apresenta $$$E$ e escreve insistentemente $$$\ nabla \ mathbf {F}$ em vez de $$$\ nabla E$ , embora calcule exatamente $$$\ nabla E$ .

Como resultado, a descida do gradiente leva à seguinte condição: para compensar o desvio de orientação, um novo termo negativo proporcional à equação cinemática deve ser adicionado a partir da equação cinemática $$$\ nabla E$ :

$$

$$\ ponto {\ mathbf {q}} = \ frac {1} {2} \ mathbf {q} \ mathbf {\ omega} - \ beta \ frac {\ nabla E} {| \ nabla E |}$$

Aqui Majwik se afasta um pouco do nosso “princípio básico”: ele não adiciona o termo de correção à velocidade angular, mas à taxa de mudança do quaternion, e isso não é exatamente a mesma coisa. Como resultado, pode acontecer que o quaternário atualizado deixe de ser solteiro e, consequentemente, perca a capacidade de representar orientação. Portanto, para o filtro Majwik, a normalização artificial do quaternião é uma operação vital, enquanto para outros filtros é desejável, não opcional.

O efeito da aceleração

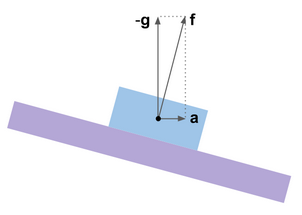
Até agora, assumiu-se que não existem acelerações verdadeiras e os acelerômetros medem apenas a aceleração gravitacional $$$- \ mathbf {g}$ . Isso tornou possível obter um padrão vertical e, com sua ajuda, compensar a deriva de rotação e inclinação. No entanto, no caso geral, os acelerômetros, independentemente do princípio de operação, medem a aceleração aparente - a diferença vetorial da verdadeira aceleração e da aceleração gravitacional. $$$\ mathbf {f.} = \ mathbf {a} - \ mathbf {g}$ . A direção da aceleração aparente não coincide com a vertical, e os erros causados ​​pelas acelerações aparecem nas estimativas de rotação e inclinação.

Isso é fácil de ilustrar usando a analogia de uma plataforma de giroscópio virtual. Seu sistema de correção é projetado para que a plataforma pare nessa posição angular na qual os sinais dos acelerômetros, supostamente instalados nele, sejam redefinidos para zero, ou seja, quando o vetor medido $$$\ mathbf {f.}$ torna-se perpendicular aos eixos da sensibilidade dos acelerômetros. Se não houver aceleração, essa posição coincide com o horizonte. Quando ocorrem acelerações horizontais, a plataforma giroscópica é desviada. Podemos dizer que a plataforma giroscópica é semelhante a um pêndulo ou linha de prumo fortemente amortecidos.



Nos comentários da postagem sobre o filtro Majwik, surgiu uma pergunta sobre se é possível esperar que esse filtro seja menos suscetível a acelerações do que, por exemplo, o filtro Mahoney. Infelizmente, todos os filtros descritos aqui exploram os mesmos princípios físicos e, portanto, sofrem dos mesmos problemas. É impossível enganar a física com a matemática. O que fazer então?

A maneira mais simples e mais difícil foi inventada em meados do século passado para os giro-verticais da aviação: reduzir ou zerar completamente a velocidade angular de controle na presença de acelerações ou a velocidade angular do curso (que indica a entrada em uma curva). O mesmo método pode ser aplicado aos sistemas de plataforma atuais. Nesse caso, as acelerações devem ser julgadas pelos valores $$$\ hat {f} _ {N}, \ hat {f} _ {E}$ mas não $$$\ hat {f} _ {x}, \ hat {f} _ {y}$ que por sua vez são zero. No entanto em tamanho $$$\ hat {\ mathbf {f.}} _ {NED}$ nem sempre é possível distinguir acelerações verdadeiras de projeções de aceleração gravitacional, devido à inclinação da plataforma giroscópica, que deve ser eliminada. Portanto, o método não funciona de maneira confiável - mas não requer sensores adicionais.

Um método mais preciso é baseado no uso de medições externas de velocidade do receptor GNSS. Se a velocidade é conhecida $$$\ mathbf {v}$ , então ele pode ser diferenciado numericamente e obter verdadeira aceleração $$$\ ponto {\ mathbf {v}}$ . Então a diferença $$$\ hat {\ mathbf {f}} _ {NED} - \ ponto {\ mathbf {v}}$ será exatamente igual $$$- \ hat {\ mathbf {g}} _ {NED}$ independentemente do movimento da mídia. Pode ser usado como padrão vertical. Por exemplo, você pode especificar a velocidade angular de controle da plataforma giroscópica no formato

$$

$$\ omega '_ {N} = gk_ {g} (\ hat {f} _ {E} - \ ponto {v} _ {E}), \; \ omega '_ {E} = - gk_ {g} (\ hat {f} _ {N} - \ ponto {v} _ {N})$$

Compensações zero do sensor

Uma característica triste dos giroscópios e acelerômetros de nível consumidor é a grande instabilidade de compensações nulas no tempo e na temperatura. Para eliminá-los, apenas a calibração de fábrica ou de laboratório não é suficiente - você precisa reavaliar durante a operação.

Giroscópios. Vamos lidar com zero deslocamentos de giroscópios $$$\ delta {\ mathbf {\ omega}}$ . A posição estimada do sistema de coordenadas associado se afasta de sua posição real com uma velocidade angular determinada por dois fatores opostos - deslocamento zero dos giroscópios e controle da velocidade angular: $$$\ delta {\ mathbf {\ omega}} - \ mathbf {\ omega '}$ . Se o sistema de correção (por exemplo, no filtro Mahoney) conseguiu parar a saída, no estado estacionário será $$$\ delta {\ mathbf {\ omega}} = \ mathbf {\ omega '}$ . Em outras palavras, na velocidade angular de controle $$$\ mathbf {\ omega '}$ informações sobre uma perturbação válida desconhecida $$$\ delta {\ mathbf {\ omega}}$ . Portanto, a estimativa compensatória pode ser aplicada: não sabemos diretamente a magnitude da perturbação; no entanto, sabemos que ação corretiva é necessária para equilibrá-la. Essa é a base para estimar o deslocamento zero dos giroscópios. Por exemplo, em Mahoney, a pontuação é atualizada de acordo com a lei

$$

$$\ ponto {\ hat {\ delta \ mathbf {\ omega}}} = k_ {b} \ mathbf {\ omega '}$$

No entanto, o resultado é estranho: as estimativas atingem 0,04 rad / s. Essa instabilidade de compensações nulas não ocorre mesmo nos giroscópios mais desagradáveis. Eu suspeito que o problema é que o Mahoney não usa GNSS ou outros sensores externos - e é totalmente afetado pela influência das acelerações. Somente no eixo vertical, onde a aceleração não prejudica, a estimativa parece mais ou menos robusta:


Mahony et al., 2008

Acelerômetros Acelerômetros com deslocamento zero de taxa $$$\ delta {\ mathbf {f.}}$ muito mais difícil. As informações sobre eles devem ser extraídas da mesma velocidade angular de controle $$$\ mathbf {\ omega '}$ . No entanto, em movimento retilíneo, o efeito de deslocamento zero dos acelerômetros é indistinguível da inclinação do transportador ou da inclinação da instalação do bloco sensor nele. 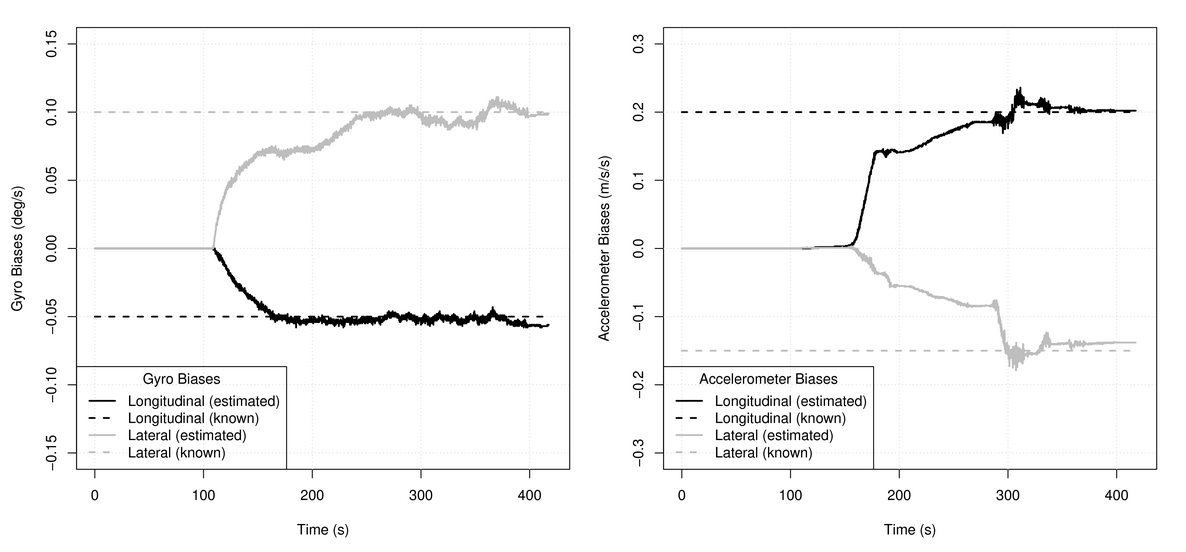Sem aditivos para $$$\ mathbf {\ omega '}$ acelerômetros não criam. O aditivo aparece apenas em uma curva, o que nos permite separar e avaliar independentemente os erros dos giroscópios e acelerômetros. Um exemplo de como isso pode ser feito está no meu artigo . Aqui estão as fotos de lá:

Em vez de uma conclusão: e o filtro de Kalman?

Não tenho dúvidas de que os filtros descritos aqui quase sempre terão uma vantagem sobre o filtro Kalman tradicional em termos de velocidade, compacidade do código e facilidade de configuração - para isso, foram criados. Quanto à precisão da avaliação, aqui tudo não é tão claro. Conheci filtros Kalman desenhados sem sucesso, que em precisão eram notavelmente inferiores a um filtro com uma plataforma de giroscópio virtual. Majwik também provou os benefícios de seu filtro em relação a algumas estimativas de Kalman. No entanto, para a mesma tarefa de estimativa de orientação, é possível construir pelo menos uma dúzia de circuitos de filtro Kalman diferentes, e cada um terá inúmeras configurações. Não tenho motivos para pensar que o filtro Mahoney ou Majwik será mais preciso do que o melhor filtro Kalman possível . E, é claro, a abordagem de Kalman sempre terá a vantagem da universalidade: não impõe restrições estritas às propriedades dinâmicas específicas do sistema avaliado.