Parte 2. Combustível Muito Pesado
Parte anterior 1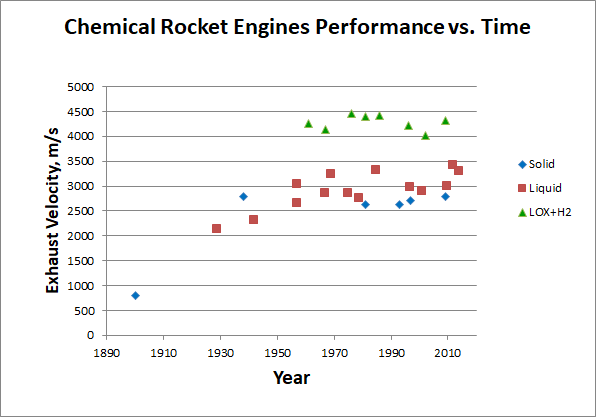
Antes de você é a Estação Espacial Internacional. Com uma massa de 420 toneladas e um valor de
[ 20 ] de US $ 150 bilhões:

Sua energia cinética, o bom e velho
E =
mv 2/2 , é de 1,3 x 10
13 joules. Adicionando energia potencial a uma altitude de 400 quilômetros, obtemos 1,4 * 10
13 J.
Quanto gás você precisa queimar para obter essa energia? Acontece que nem tanto. 350 toneladas no total. Este é aproximadamente o
[ 200 ] orçamento energético de um dia de Ulan-Ude.
Como é que longe da cidade mais rica do mundo em um único dia gerencia energia suficiente para acelerar a ISS à velocidade orbital, no entanto, temos uma estação para o mundo inteiro e custa dinheiro indecentemente louco?
A resposta
está no óbvio da anatomia do veículo de lançamento.
A transportadora, no mínimo, deve incluir:
- Carga útil. Caso contrário, por que é necessário?
- Pelo menos um motor.
- Uma habitação que conecta tudo isso.
- E, claro, combustível. Como fluido de trabalho e, na maioria dos casos, como fonte de energia.
E no último parágrafo, o problema está enraizado. Para elevar e arrastar um certo mínimo de combustível, você precisa ... corretamente, de combustível adicional! Na ascensão da qual você também precisa de combustível! E essa embalagem dura muito tempo. É claro que converge, caso contrário não voaríamos para lugar nenhum. Mas, de acordo com os resultados da convergência, um foguete moderno, mesmo de vários estágios e até de alta qualidade projetado e executado, em massa, consiste principalmente desse combustível.
Bem, aqui está um exemplo de livro didático, Saturno V não é o mais novo, mas um dos mísseis mais eficazes da história
[ 30 ] :

[Imagem original da História da NASA [
40 ]]
Peso inicial - 2970 toneladas. Cerca de 2670 deles são combustíveis. Dos quais 2160 queimam em menos de três minutos de toda a expedição lunar. Apesar do fato de que a energia cinética da carga em órbita "custa" apenas 100 toneladas de combustível.
Acontece que a principal dificuldade em entrar em órbita não é a falta de energia. Seus terráqueos têm abundantemente energia cinética não apenas para as estações, mas também para navios de cruzeiro em órbita. O problema é diferente: nosso combustível é muito pesado. Muito disso é necessário em quilogramas para coletar a quantidade de energia necessária para o voo. Por
que a maior parte do combustível derramado no foguete
seria destinada ao transporte de combustível? Na verdade, a fórmula de Tsiolkovsky, que liga o
M inicial e a massa final do foguete
m com a velocidade ganha
V e a velocidade de escape do motor
u , nos diz a mesma coisa:
M /
m = e
V / u [2]
À primeira vista, não é totalmente óbvio o que o conteúdo de energia por quilograma tem a ver com isso? Mas tudo é simples. Ele "senta" em
você , na taxa de vencimento. Para combustível químico, ele é limitado por (e a uma primeira aproximação igual a)
u = √ (2
q ), onde
q é o calor específico da combustão. Qual é o conteúdo energético por quilograma. E quando esse
q "fica aquém", a proporção de massa no início e no final acaba sendo exponencialmente grande:
M /
m = e
V / √ (2 q ) [3]
Ou
V = Ln (
M /
m ) * √ (
2q ) [3a]
Algumas notas, para nerds e para maior clareza1. Sim, existem expressões mais precisas para a vazão do que
u = √ (
2q ). Quando passei o crédito por eles, Gorbachev "entregou" a URSS. Mas essas fórmulas são complicadas, assustam os leitores e levam em conta efeitos que não são importantes aqui.
u = √ (
2q ), embora exagere em 10 a 30% a resposta, descreve adequadamente a dependência de interesse para nós. E sim, existe um impulso específico, mas neste artigo em particular, a taxa de fluxo é mais conveniente de usar.
2. Em princípio, nada proíbe nem mesmo um foguete químico obter uma velocidade de vazão
u superior a √ (2
q ). Como Bem, digamos, queimar combustível não em um bico, mas em um gerador, gerando energia elétrica. Então, com essa energia, acelere a fração
x do escapamento (0 <
x ≤ 1) para velocidades muito altas. Por exemplo, um motor a jato elétrico a plasma
[ 230 ] . E os resíduos de exaustão são estupidamente jogados na velocidade zero. Por simplicidade, assumimos que todas as transformações ocorrem sem perda de energia, com 100% de eficiência. Um foguete desse tipo acelerará para uma velocidade mais alta
V com uma razão de massa fixa
M /
m (isto é, será mais eficaz)?
A resposta é não. É fácil resolver as equações que descrevem o movimento de um foguete e obter:
V = Ln (
M /
m ) * √ (
2qx )
I.e. sua velocidade final será apenas √
x do foguete “comum” digitado com combustão direta de combustível (cf. [3a]). E essa velocidade ainda está rigidamente ligada a
q .
3. E se o foguete não funcionar com combustível, mas com bateria? Bem, deixe haver um meio de trabalho separado de massa
m f a bordo e separadamente uma bateria com uma reserva de energia
E e massa
m b .
A primeira coisa que você precisa entender aqui é que a bateria deve consistir em muitos "módulos" pequenos que são redefinidos à medida que funcionam. Caso contrário, carregaremos conosco a carga "morta" de baterias vazias. Mas, nesse caso, conceitualmente, isso não difere do combustível comum a bordo com uma reserva total de energia
E e massa
m f +
m b . E se
q =
E / (
m f +
m b ) desse sistema for menor que o de um foguete químico convencional, ele não voará melhor.
5. Mas e os motores de foguete elétrico
[ 225 ] ? Afinal, eles fornecem vazões de dezenas e centenas de quilômetros por segundo e realizaram manobras interplanetárias bem-sucedidas com taxas
M /
m muito modestas. Como assim? O fato é que os ERDs são sistemas abertos. Eles carregam o fluido de trabalho (mercúrio, xenônio etc.) com eles. Mas energia não é. A energia vem de painéis solares. Se, em vez disso, eles carregassem baterias comuns com um conteúdo energético de massa
q , então sua eficiência não seria maior, de acordo com a fórmula [3a].
O artigo foi escrito para o site https://habr.com . Ao copiar, consulte a fonte. O autor do artigo é Evgeny Bobukh .Portanto, os mísseis são caros porque seu design "leve" extremamente leve é forçado a suportar uma carga extremamente pesada, principalmente combustível (e até "bombeá-lo" rapidamente pelo TNA). E a carga é ótima porque nosso combustível é muito pesado. Muito pouco é colocado em joules por quilograma.
Vamos agora entender as razões dessa limitação.
Por que olhar mais de perto a reação da combustão de hidrogênio no flúor, como uma das mais simples. Nele, os pares hidrogênio-hidrogênio e flúor-flúor trocam de parceiros, criando dois pares hidrogênio-flúor:
H2 +
F2 = 2
HFDe onde vem a energia liberada?
Uma molécula de hidrogênio tem dois átomos. Os átomos têm elétrons. Eles são "borrados" ao redor do átomo na forma de uma espécie de nuvem e estão conectados ao núcleo principalmente por atração eletrostática. Os elétrons são externos, valência e (exceto hidrogênio) interno, não participam de reações químicas. Após a reação, hidrogênio e flúor mudam de lugar. Nuvens elétricas de elétrons de valência são redistribuídas e mudam ligeiramente de forma. Algo assim:
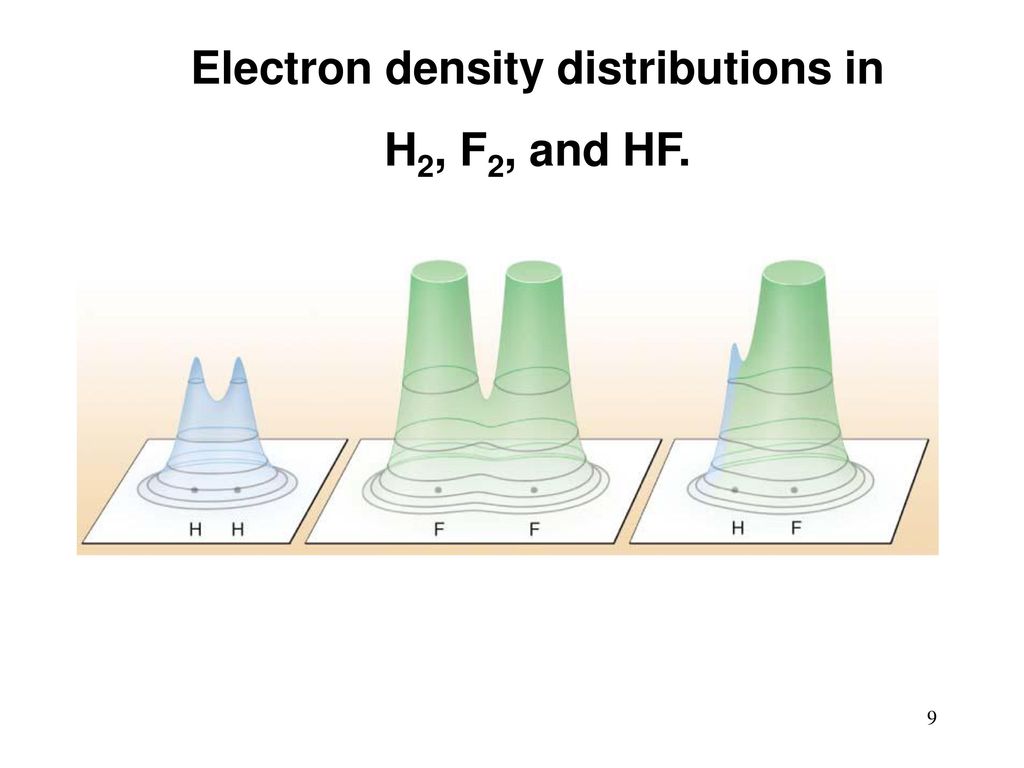
[Crédito de imagem [
295 ]]
A energia potencial de ligação de elétrons com átomos em novas nuvens é diferente. Nesse caso (essa energia é negativa), agora é menor que a de
H2 e
F 2 separadamente. Para onde foi a diferença? A energia cinética de uma molécula, as vibrações de seus átomos, radiação eletromagnética. Tudo isso acabou se transformando em calor. O que expandiu o gás e deu tração.
E aqui está o momento crítico. Somente elétrons de valência externos estão envolvidos em reações químicas. A distribuição de densidade de outros elétrons (assim como o campo elétrico "na profundidade" do átomo) permanece praticamente inalterada. Nas reações químicas, os átomos interagem entre si como se fossem "intermediários", que são elétrons de valência:
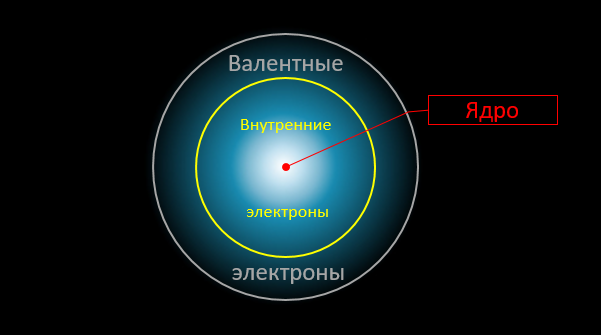
Agora, atenção, a pergunta é: qual é a energia máxima possível que pode ser liberada durante essa "permutação"? Obviamente, não pode exceder a soma das energias de ligação de elétrons externos com átomos (no produto final e inicial). Mas essas energias de ligação são bem conhecidas por nós
[ 285 ] . Por átomo, eles equivalem a 1,5 - 25
elétron-volts (
eV ) e são expressos em frações da constante de Rydberg - um valor fundamental construído a partir das constantes básicas do nosso Universo:
Ry (no sistema gaussiano) =
m e e 4/2 ħ 2 =
1 3 .6 eV [
300 ]
Além disso, 25 e 13,6 eV são inatingíveis. Pois em reações típicas longe de toda a energia de ligação é liberada, mas apenas a diferença entre as duas configurações e, portanto, o teto prático da liberação de energia da química é de 3-4 eV por átomo. Em termos de um quilograma típico de combustível + oxidante, isso equivale a 20-30 MJ de energia liberada. É essa quantidade que define a velocidade máxima teórica do gás de um motor a jato químico com combustão direta
u = √ (2
q ) = √ (2 * 2,5 * 10
7 ) ≈ 7000 m / s. Inatingível, é claro, porque não leva em conta as perdas nos graus internos de liberdade de moléculas, dissociação, radiação, movimento térmico não direcional, etc.
Pode parecer que aquecimentos tabulares de combustão
[ 240 ] (digamos, 120 MJ / kg de hidrogênio) contradizem a figura escrita acima. Mas o fato é que esses aquecimentos são geralmente indicados por quilograma de
combustível , sem levar em conta o oxidante necessário para sua combustão. O foguete carrega os dois componentes e, se recalcularmos a energia liberada por quilograma da
mistura (com combustão equilibrada), uma imagem completamente diferente surge
[ 240 ] [ 250 ] [ 260 ] :
| Combustível + oxidante | Reacção | Valor calorífico por kg. combustível, MJ / kg | 1 kg de combustível precisa de um oxidante, kg. | Valor calorífico, MJ / kg | A produção por átomo da mistura, eV |
| Hidrogênio + oxigênio | 2H 2 + O 2 = 2H 2 O | 120 | 8 | 13,3 | 0,83 |
| Querosene + oxigênio | 2C 12 H 26 + 37O 2 = 24CO 2 + 26H 2 O | 43 | 3.5 | 9,6 | 1.02 |
| Carvão + Oxigênio | C + O 2 = CO 2 | 33 | 2.7 | 9.0 | 1,38 |
| Lítio + oxigênio | 4Li + O 2 = 2Li 2 O | 43,5 | 1.2 | 20,2 | 2.10 |
| Boro + Oxigênio | 2B + 1,5O 2 = B 2 O 3 | 57,2 | 2.2 | 17,8 | 2,58 |
| Magnésio + Oxigênio | 2Mg + O 2 = 2MgO | 25,1 | 0,7 | 15.1 | 3,18 |
| Berílio + oxigênio | 2Be + O 2 = 2BeO | 66,6 | 1.8 | 24,0 | 3,12 |
| Lítio + flúor | 2Li + F 2 = 2LiF | 88,8 | 2.7 | 23,7 | 3,21 |
| Berílio + Fluoreto | Seja + F 2 = BeF 2 | 114 | 4.2 | 21,9 | 3.57 |
| Dicianoacetileno + ozônio | C 4 N 2 + (4/3) O 3 = 4CO + N 2 | 16,2 | 0,8 | 8,8 | 1,28 |
Como você pode ver, mesmo os mais intensivos em energia, embora inadequados para uso prático, os combustíveis fornecem apenas 24 MJ / kg de calor durante a combustão. E chegamos a esse limite quase desde o início da astronáutica, que mostra um gráfico da taxa de vazão de motores químicos, dependendo do ano de sua criação:

[Motores antigos de acordo com [
310 ], [
320 ], [
330 ], mais tarde - Wikipedia individualmente. Coleta de dados
aqui ]
Parece que o potencial do combustível químico já foi desenvolvido. É possível começar a armazenar energia de outra forma?
Para ser continuado.