Entrada
Neste artigo, falarei sobre o conhecido algoritmo Huffman, bem como sua aplicação na compactação de dados.
Como resultado, escreveremos um arquivador simples. Já havia um
artigo sobre Habré , mas sem implementação prática. O material teórico da publicação atual é retirado das aulas de ciências da computação da escola e do livro de Robert Lafore "Estruturas de dados e algoritmos em Java". Então, está tudo em ordem!
Um pouco de reflexão
Em um arquivo de texto sem formatação, um caractere é codificado com 8 bits (codificação ASCII) ou 16 (codificação Unicode). Além disso, consideraremos a codificação ASCII. Por exemplo, pegue a linha s1 = "SUSIE DIZ QUE É FÁCIL \ n". No total, é claro que existem 22 caracteres na linha, incluindo espaços e o caractere de nova linha - '\ n'. Um arquivo contendo esta linha pesa 22 * 8 = 176 bits. Surge imediatamente a pergunta: é racional usar todos os 8 bits para codificar um caractere? Nós não usamos todos os caracteres ASCII. Mesmo se usado, seria mais racional para a letra mais frequente - S - fornecer o menor código possível e para a letra mais rara - T (ou U, ou '\ n') - fornecer um código mais autêntico. Este é o algoritmo de Huffman: você precisa encontrar a melhor opção de codificação, na qual o arquivo terá peso mínimo. É bastante normal que os comprimentos do código sejam diferentes para caracteres diferentes - essa é a base do algoritmo.
Codificação
Por que não atribuir ao caractere 'S' um código, por exemplo, com 1 bit de comprimento: 0 ou 1. Seja 1. Então, forneceremos o segundo caractere mais encontrado - '' (espaço) - 0. Imagine que você começou a decodificar sua mensagem - sequência codificada s1 - e você vê que o código começa com 1. Então, o que fazer: é um caractere S ou algum outro caractere, por exemplo A? Portanto, surge uma regra importante:
Nenhum código deve ser o prefixo de outroEsta regra é a chave no algoritmo. Portanto, a criação do código começa com a tabela de frequências, que indica a frequência (número de ocorrências) de cada caractere:
Os caracteres com mais ocorrências devem ser codificados com o menor número
possível de bits. Vou dar um exemplo de uma das tabelas de código possíveis:
Assim, a mensagem codificada ficará assim:
10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110
Separei o código de cada caractere com um espaço. Isso realmente não acontecerá em um arquivo compactado!
Surge a pergunta:
como essa sálaga surgiu com um código ? Como criar uma tabela de códigos? Isso será discutido abaixo.
Construindo uma árvore huffman
Aqui, as árvores de busca binária vêm em socorro. Não se preocupe, aqui os métodos de busca, inserção e exclusão não são necessários. Aqui está a estrutura da árvore em java:
public class Node { private int frequence; private char letter; private Node leftChild; private Node rightChild; ... }
class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } ... }
Este não é um código completo, o código completo estará abaixo.
Aqui está o próprio algoritmo de construção de árvore:
- Crie um objeto Nó para cada caractere da mensagem (linha s1). No nosso caso, haverá 9 nós (objetos Node). Cada nó consiste em dois campos de dados: símbolo e frequência
- Crie um objeto de árvore (BinaryTree) para cada um dos nós do nó. O nó se torna a raiz da árvore.
- Cole essas árvores na fila de prioridade. Quanto menor a frequência, maior a prioridade. Assim, ao extrair, o dervo é sempre selecionado com a menor frequência.
Em seguida, você precisa fazer o seguinte ciclicamente:
- Extraia duas árvores da fila de prioridade e torne-as descendentes do novo nó (o nó recém-criado sem uma letra). A frequência do novo nó é igual à soma das frequências de duas árvores descendentes.
- Para este nó, crie uma árvore com uma raiz nesse nó. Cole esta árvore de volta na fila de prioridade. (Como a árvore tem uma nova frequência, provavelmente chegará a um novo local na fila)
- Continue as etapas 1 e 2 até restar apenas uma árvore na fila - a árvore Huffman
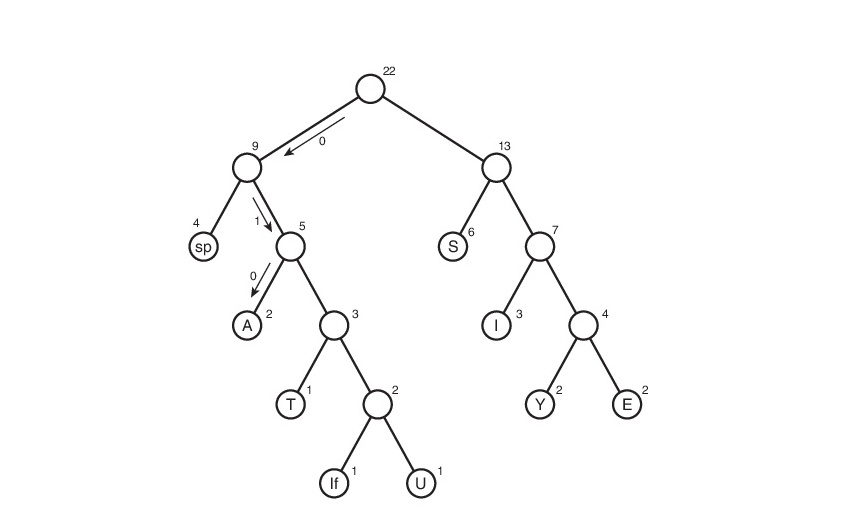
Considere este algoritmo na linha s1:

Aqui, o símbolo "lf" (avanço de linha) indica a transição para uma nova linha, "sp" (espaço) é um espaço.
O que vem a seguir?
Temos uma árvore Huffman. Bem, tudo bem. E o que fazer com isso?
Eles não o levam de graça e, então, você precisa acompanhar todos os caminhos possíveis, desde a raiz até as folhas da árvore. Vamos concordar em designar a aresta 0 se ela levar à descendente esquerda e 1 se à direita. A rigor, nessas anotações, o código do símbolo é o caminho da raiz da árvore até a planilha que contém esse mesmo símbolo.
Assim, a tabela de códigos acabou. Observe que, se considerarmos esta tabela, podemos concluir sobre o "peso" de cada caractere - este é o comprimento do seu código. O arquivo compactado pesará: 2 * 3 + 2 * 4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 bits. Inicialmente, pesava 176 bits. Portanto, reduzimos em 176/65 = 2,7 vezes! Mas isso é utopia. É improvável que esse coeficiente seja obtido. Porque Isso será discutido um pouco mais tarde.
Decodificação
Bem, talvez a coisa mais simples que resta é a decodificação. Acho que muitos de vocês imaginaram que é impossível simplesmente criar um arquivo compactado sem nenhuma dica de como ele foi codificado - não poderemos decodificá-lo! Sim, foi difícil para mim perceber isso, mas tive que criar um arquivo de texto table.txt com uma tabela de compactação:
01110 00 A010 E1111 I110 S10 T0110 U01111 Y1110
Registre a tabela na forma de 'caractere' "código de caractere". Por que 01110 é sem caractere? De fato, é com um símbolo, apenas as ferramentas java usadas por mim ao gerar um arquivo, o caractere de nova linha - '\ n' - é convertido em uma nova linha (por mais estúpido que pareça). Portanto, a linha vazia na parte superior é o caractere para o código 01110. Para o código 00, o caractere é um espaço no início da linha. Devo dizer imediatamente que
nosso método de armazenar esta tabela pode reivindicar o mais irracional. Mas é simples de entender e implementar. Terei o prazer de ouvir suas recomendações nos comentários sobre otimização.
Ter essa tabela é muito fácil de decodificar. Lembre-se de qual regra fomos guiados ao criar a codificação:
Nenhum código deve prefixar outroÉ aqui que ele desempenha um papel facilitador. Lemos sequencialmente bit a bit e, assim que a sequência recebida d, composta por bits de leitura, corresponde à codificação correspondente ao caractere, sabemos imediatamente que o caractere foi codificado (e somente ele!). Em seguida, escrevemos caracteres na linha de decodificação (a linha que contém a mensagem decodificada), zeramos a linha d e lemos o arquivo codificado.
Implementação
É hora de
humilhar meu código escrevendo um arquivador. Vamos chamá-lo de compressor.
Vamos começar do começo. Primeiro, escrevemos a classe Node:
public class Node { private int frequence;
Agora a árvore:
class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } public int getFrequence() { return root.getFrequence(); } public Node getRoot() { return root; } }
Fila prioritária:
import java.util.ArrayList;
A classe que cria a árvore Huffman:
public class HuffmanTree { private final byte ENCODING_TABLE_SIZE = 127;
Classe que contém quais codificações / decodificações:
public class HuffmanOperator { private final byte ENCODING_TABLE_SIZE = 127;
Classe que facilita a gravação em um arquivo:
import java.io.File; import java.io.PrintWriter; import java.io.FileNotFoundException; import java.io.FileOutputStream; import java.io.IOException; import java.io.Closeable; public class FileOutputHelper implements Closeable { private File outputFile; private FileOutputStream fileOutputStream; public FileOutputHelper(File file) throws FileNotFoundException { outputFile = file; fileOutputStream = new FileOutputStream(outputFile); } public void writeByte(byte msg) throws IOException { fileOutputStream.write(msg); } public void writeBytes(byte[] msg) throws IOException { fileOutputStream.write(msg); } public void writeString(String msg) { try (PrintWriter pw = new PrintWriter(outputFile)) { pw.write(msg); } catch (FileNotFoundException e) { System.out.println(" , !"); } } @Override public void close() throws IOException { fileOutputStream.close(); } public void finalize() throws IOException { close(); } }
Classe que facilita a leitura de um arquivo:
import java.io.FileInputStream; import java.io.EOFException; import java.io.BufferedReader; import java.io.InputStreamReader; import java.io.Closeable; import java.io.File; import java.io.IOException; public class FileInputHelper implements Closeable { private FileInputStream fileInputStream; private BufferedReader fileBufferedReader; public FileInputHelper(File file) throws IOException { fileInputStream = new FileInputStream(file); fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream)); } public byte readByte() throws IOException { int cur = fileInputStream.read(); if (cur == -1)
Bem, e a classe principal:
import java.io.File; import java.nio.charset.MalformedInputException; import java.io.FileNotFoundException; import java.io.IOException; import java.nio.file.Files; import java.nio.file.NoSuchFileException; import java.nio.file.Paths; import java.util.List; import java.io.EOFException; public class Main { private static final byte ENCODING_TABLE_SIZE = 127; public static void main(String[] args) throws IOException { try {
O arquivo de instruções readme.txt depende de você escrever :-)
Conclusão
Provavelmente é tudo o que eu queria dizer. Se você tem algo a dizer sobre a
minha incompetência de melhorias no código, algoritmo e qualquer otimização em geral, fique à vontade para escrever. Se eu entendi algo errado, também escreva. Ficarei feliz em ouvi-lo nos comentários!
PS
Sim, sim, ainda estou aqui, porque não esqueci o coeficiente. Para a string s1, a tabela de codificação pesa 48 bytes - muito mais que o arquivo original e eles não esqueceram de zeros adicionais (o número de zeros adicionados é 7) => a taxa de compactação será menor que um: 176 / (65 + 48 * 8 + 7) = 0,38. Se você também notou isso, então
não apenas na cara, você está bem feito. Sim, essa implementação será extremamente ineficiente para arquivos pequenos. Mas o que acontece com arquivos grandes? Os tamanhos dos arquivos excedem em muito o tamanho da tabela de codificação. Aqui o algoritmo funciona como deveria! Por exemplo, para o
monólogo Faust, o arquivador fornece um coeficiente real (não idealizado) igual a 1,46 - quase uma vez e meia! E sim, o arquivo deveria estar em inglês.