Escrevendo o XGBoost a partir do zero - parte 1: árvores de decisão

Olá Habr!

Após inúmeras pesquisas por guias de alta qualidade sobre árvores de decisão e algoritmos de conjunto (reforço, floresta de decisão etc.) com sua implementação direta em linguagens de programação e sem encontrar nada (quem encontrar - escreva nos comentários, talvez eu aprenda algo novo), Decidi fazer minha própria liderança, como gostaria de vê-la. A tarefa em palavras é simples, mas, como você sabe, o diabo está nas pequenas coisas, das quais existem muitos algoritmos com árvores.

Como o tópico é bastante extenso, será muito difícil incluir tudo em um artigo; portanto, haverá duas publicações: a primeira é dedicada às árvores e a segunda parte será dedicada à implementação do algoritmo de aumento de gradiente. Todo o material apresentado aqui é compilado e projetado com base em fontes abertas, meu código, o código de colegas e amigos. Eu te aviso imediatamente, haverá muito código.



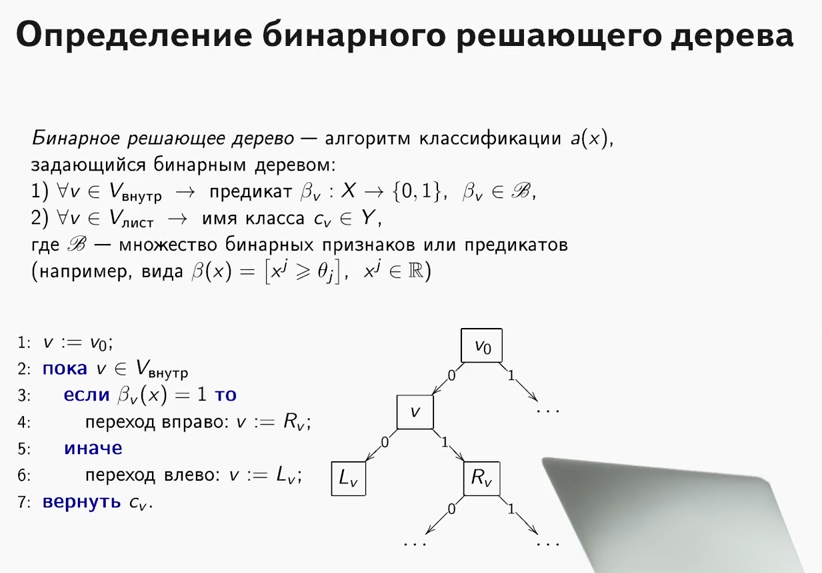
Então, o que você precisa saber e ser capaz de aprender a escrever seus próprios algoritmos de conjunto com árvores de decisão do zero? Como um conjunto de algoritmos nada mais é do que uma composição de “algoritmos fracos”, escrever um bom conjunto requer bons “algoritmos fracos”, iremos analisá-los em detalhes neste artigo. Como o nome indica, essas são árvores cruciais e, passando de simples para complexas, aprenderemos como escrevê-las. Nesse caso, a ênfase será colocada diretamente na implementação, toda a teoria será apresentada no mínimo, basicamente darei links para materiais para estudo independente.

Para aprender o material, você precisa entender o quão bom ou ruim é o nosso algoritmo. Nós entenderemos com muita simplicidade - corrigiremos alguns conjuntos de dados específicos e compararemos nossos algoritmos com os algoritmos de árvores do Sklearn (bem, o que aconteceria sem essa biblioteca). Vamos comparar muito: a complexidade do algoritmo, métricas de dados, tempo de atividade etc.

O que é uma árvore decisiva? Um material muito bom, que explica o princípio da árvore de decisão, está contido no curso da ODS (a propósito, um curso interessante, eu o recomendo para aqueles que começam a conhecer o ML).

Uma explicação muito importante: em todos os casos descritos abaixo, todos os sinais serão reais, não faremos transformações especiais com dados fora dos algoritmos (comparamos algoritmos, não conjuntos de dados).

Agora vamos aprender como resolver o problema de regressão usando árvores de decisão. Usaremos a métrica MSE como entropia.

Implementamos uma classe RegressionTree muito simples, baseada em uma abordagem recursiva. Intencionalmente, começamos com uma implementação muito ineficaz, mas fácil de entender, de uma classe para poder melhorá-la no futuro.

1. Classe RegressionTree ()

 class RegressionTree(): '''  RegressionTree   .    ,      . ''' def __init__(self, max_depth=3, n_epoch=10, min_size=8): '''   . ''' self.max_depth = max_depth #   self.min_size = min_size #    self.value = 0 #    (   ) self.feature_idx = -1 #    self.feature_threshold = 0 #    self.left = None #   self.right = None #   def fit(self, X, y): '''   .     . ''' #    self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #       prev_error_left = base_error prev_error_right = 0 #     0 -  if self.max_depth <= 1: return dim_shape = X.shape[1] #       left_value = 0 right_value = 0 #     for feat in range(dim_shape): #   idxs = np.argsort(X[:, feat]) #        N = X.shape[0] N1, N2 = N, 0 thres = 1 #      while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #    if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue # ,         target_right = y[idxs][:thres] target_left = y[idxs][thres:] mean_right = y[idxs][:thres].mean(), mean_left = y[idxs][thres:].mean() #        - #   (  ) left_shape = target_left.shape[0] right_shape = target_right.shape[0] mean_left_array = [mean_left for _ in range(left_shape)] mean_right_array = [mean_right for _ in range(right_shape)] #      prev_error_left = N1/N * mse(target_left, mean_left_array) prev_error_right = N2/N * mse(target_right, mean_right_array) #    ,   if (prev_error_left + prev_error_right < error): if (min(N1,N2) > self.min_size): self.feature_idx = feat self.feature_threshold = x left_value = mean_left right_value = mean_right flag = 1 error = prev_error_left + prev_error_right thres += 1 #     ,  if self.feature_idx == -1: return #   -   ,    #   -     self.left = RegressionTree(self.max_depth - 1) self.left.value = left_value self.right = RegressionTree(self.max_depth - 1) self.right.value = right_value #   idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #  self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): '''     -  ,         self.value -    . ''' if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): '''    -      __predict(). ''' y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Vou explicar brevemente o que cada método faz aqui.

O método de fit , como o nome indica, ensina o modelo. Uma amostra de treinamento é aplicada à entrada e ocorre um procedimento de treinamento em árvore. Classificando os sinais, estamos procurando a melhor partição da árvore em termos de redução da entropia, neste caso mse . Para determinar que era possível encontrar uma boa divisão, é muito simples, basta atender a duas condições. Não queremos que poucos objetos caiam na partição (proteção contra reciclagem), e o erro médio para o mse deve ser menor que o erro que está agora na árvore - estamos procurando o mesmo ganho no ganho de informações . Depois de passar por todos os sinais e todos os valores únicos dessa maneira, examinaremos todas as opções e escolheremos a melhor partição. E então fazemos uma chamada recursiva nas partições recebidas até que as condições para sair da recursão sejam satisfeitas.

O método __predict , como o nome indica, __predict um predicado. Tendo recebido um objeto como entrada, ele passa pelos nós da árvore resultante - em cada nó o número e o valor do atributo são fixados nele, e dependendo do valor que o método de entrada do objeto usa para esse atributo, vamos para o descendente direito ou para a esquerda, até chegarmos à planilha, na qual haverá uma resposta para esse objeto.

O método de predict faz o mesmo que o método anterior, apenas para um grupo de objetos.

Importamos o conhecido conjunto de dados domésticos da Califórnia. Este é um conjunto de dados regular com dados e um alvo para resolver o problema de regressão.

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) 

Bem, vamos começar a comparação! Primeiro, vamos ver a rapidez com que o algoritmo aprende. Definimos no Sklearn e em nós mesmos o único parâmetro max_depth , que seja igual a 2.

 %%time A = RegressionTree(2) #    A.fit(X,y) 

 from sklearn.tree import DecisionTreeRegressor %%time model = DecisionTreeRegressor(max_depth=2) #  Sklearn model.fit(X,y) 

O seguinte será exibido:

• Para o nosso algoritmo - tempos de CPU: usuário 4min 47s, sys: 8,25 ms, total: 4min 47s
  Tempo de parede: 4min 47s
• Para Sklearn - tempos de CPU: usuário 53,5 ms, sys: 0 ns, total: 53,5 ms
  Tempo de parede: 53,4 ms

Como você pode ver, o algoritmo aprende milhares de vezes mais devagar. Qual o motivo? Vamos acertar.

Lembre-se de como é organizado o procedimento para encontrar a melhor partição. Como você sabe, no caso geral, com o tamanho dos objetos $$$N$e com o número de sinais $$$d$, a dificuldade de encontrar a melhor divisão é $$$O (N * logN * d)$.

De onde vem essa complexidade?

Primeiro, para recalcular efetivamente o erro, é necessário classificar todas as colunas para passar da menor para a maior antes de passar pelo atributo. À medida que fazemos isso para cada característica, isso cria uma complexidade correspondente. Como você pode ver, classificamos os sinais, mas o problema está em recalcular o erro - cada vez que direcionamos os dados para o método mse , que funciona para a linha. Isso torna a recontagem de erros tão ineficiente! Afinal, a dificuldade de encontrar uma divisão aumenta para $$$O (N ^ 2 * d)$para grandes $$$N$retarda tremendamente o algoritmo. Portanto, prosseguimos sem problemas para o próximo item.

2. Classe RegressionTree () com recontagem rápida de erros

O que precisa ser feito para recontar rapidamente o erro? Pegue uma caneta e papel e pinte como devemos mudar as fórmulas.

Suponha que em alguma etapa já exista um erro calculado para $$$N$objetos. Tem a seguinte fórmula: $$$\ sum_ {i = 1} ^ n (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$. Aqui é necessário dividir por $$$N$mas por enquanto vamos omitir. Queremos obter rapidamente esse erro - $$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2$, ou seja, gere o erro que o elemento introduz $$$y_i$para outra parte.

Como lançamos o objeto, o erro deve ser recontado em dois lugares - no lado direito (excluindo este objeto) e no lado esquerdo (levando esse objeto em consideração). Mas, sem perda de generalidade, deduziremos apenas uma fórmula, uma vez que serão semelhantes.

Como trabalhamos com mse , não tivemos sorte: é bastante difícil obter uma recontagem rápida de um erro, mas ao trabalhar com outras métricas (por exemplo, o critério Gini, se resolvermos o problema de classificação), a recontagem rápida é muito mais fácil.

Bem, vamos começar a derivar fórmulas!

$$

$$\ sum_ {i = 1} ^ N (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 + (y_N - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$$

Escreveremos o primeiro membro:

$$

$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i + y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac { Ny_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1 } ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - 2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} + (\ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - (\ frac {y_N - y_i} {N}) ^ 2) = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - \\ - (\ frac {y_N - y_i} { N}) ^ 2)$$

Ugh, apenas um pouco para a esquerda. Resta apenas expressar a quantidade necessária.

$$

$$\ sum_ {i = 1} ^ {N} (y_i - \ frac {\ sum_ {i = 1} ^ {N} y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \\ \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) (\ frac {y_N - y_i} {N}) - (\ frac {y_N - y_i} {N}) ^ 2) + (y_N - \ sum_ {i = 1} ^ {N} \ frac {y_i} {N}) ^ 2$$

E então fica claro como expressar a quantidade desejada. Para recalcular o erro, precisamos armazenar apenas a soma dos elementos à direita e à esquerda, bem como o novo elemento em si, que chegou à entrada. Agora o erro é recontado para $$$O (1)$.

Bem, vamos implementar isso no código.

 class RegressionTreeFastMse(): '''  RegressionTree    .        O(1). ''' #    def __init__(self, max_depth=3, min_size=10): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None #   -     def fit(self, X, y): #   -   y self.value = y.mean() #   - mse     (  # ,     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2 ,    -   #   - -    if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return self.left = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Vamos medir o tempo gasto no treinamento e comparar com o analógico da Sklearn.

 %%time A = RegressionTreeFastMse(4, min_size=5) A.fit(X,y) test_mytree = A.predict(X) test_mytree 

 %%time model = DecisionTreeRegressor(max_depth=4) model.fit(X,y) test_sklearn = model.predict(X) 

• Para o nosso algoritmo, obtemos - tempos de CPU: usuário 3,11 s, sys: 2,7 ms, total: 3,11 s
  Tempo de parede: 3,11 s.
• Para o algoritmo do Sklearn - tempos de CPU: usuário 45,9 ms, sys: 1,09 ms, total: 47 ms
  Tempo de parede: 45,7 ms.

Os resultados já são mais agradáveis. Bem, vamos melhorar ainda mais o algoritmo.

3. Classe RegressionTree () com combinações lineares de recursos

Agora, em nosso algoritmo, os relacionamentos entre os atributos não são usados ​​de forma alguma. Fixamos um recurso e analisamos apenas as partições ortogonais do espaço. Como aprender a usar os relacionamentos lineares entre os atributos? Ou seja, procurar as melhores partições não é como $$$a_ {feat} <x$e $$$\ sum_ {i = 1} ^ K b_i * a_i <x$onde $$$K$- algum número é menor que a dimensão do nosso espaço?

Existem muitas opções, destacarei duas das mais interessantes do meu ponto de vista. Ambas as abordagens são descritas no livro de Friedman (ele inventou essas árvores).

Vou dar uma imagem para que fique claro o que se entende:



Primeiro, você pode tentar encontrar essas partições lineares algoritmicamente. É claro que é impossível classificar todas as combinações lineares, porque há um número infinito de combinações; portanto, esse algoritmo deve ser ganancioso, ou seja, a cada iteração, melhora o resultado da iteração anterior. A idéia principal desse algoritmo pode ser lida no livro. Também deixarei aqui um link para o repositório de meus amigos e colegas com a implementação desse algoritmo.

Em segundo lugar, se não nos afastarmos da idéia de encontrar a melhor partição ortogonal, como modificamos o conjunto de dados para que informações sobre a relação de recursos sejam usadas e a pesquisa se baseie em partições ortogonais? É isso mesmo, fazer algum tipo de transformação dos recursos originais em novos. Por exemplo, você pode pegar a soma de algumas combinações de recursos e procurar partições por eles já. Esse método se encaixa pior no conceito algorítmico, mas executa sua tarefa - ele procura partições ortogonais já em algum tipo de interconexão de atributos.

Bem, vamos implementá-lo - adicionaremos como novos recursos, por exemplo, todos os tipos de combinações de somas de recursos $$$i, j$onde $$$I <j$. Observo que a complexidade do algoritmo, neste caso, aumentará, é claro quantas vezes. Bem, para ser considerado mais rápido, usaremos o cython.

 %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeCython: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeCython left cpdef RegressionTreeCython right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.averages = averages self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def data_transform(self, np.ndarray[np.float64_t, ndim=2] X, list index_tuples): #   -       for i in index_tuples: #  ,       X = np.hstack((X, X[:, i[0]:(i[1]+1)].sum(axis=1).reshape(X.shape[0],1))) return X def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #        #  ,     if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(combinations(stuff,2)) #    X = self.data_transform(X, index_tuples) #   -   y self.value = y.mean() #   - mse     (  , #     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2    -   #   -      if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 # self.feature_idx -     . #   -  ,    -   #  ,   ,     #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeCython(self.max_depth - 1, averages=0) self.left.value = left_value self.right = RegressionTreeCython(self.max_depth - 1, averages=0) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): #   ,        if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(itertools.combinations(stuff,2)) X = self.data_transform(X, index_tuples) y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

4. Comparação de resultados

Bem, vamos comparar os resultados. Vamos comparar três algoritmos com os mesmos parâmetros - uma árvore do Sklearn, nossa árvore comum e nossa árvore com novos recursos. Dividiremos nosso conjunto de dados em conjuntos de treinamento e teste várias vezes e calcularemos o erro.

 from sklearn.model_selection import KFold def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list 

Agora vamos executar todos os algoritmos.

 import matplotlib.pyplot as plt data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_sklearn_tree = get_metrics(X,y,30,DecisionTreeRegressor(max_depth=4, min_samples_leaf=10)) er_fast_mse_tree = get_metrics(X,y,30,RegressionTreeFastMse(4, min_size=10)) er_averages_tree = get_metrics(X,y,30,RegressionTreeCython(4, min_size=10)) %matplotlib inline data = [er_sklearn_tree, er_fast_mse_tree, er_averages_tree] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Tree', 'Fast Mse Tree', 'Averages Tree']) plt.grid() plt.show() 

Resultados:



Nossa árvore comum foi perdida para o Sklearn (o que é compreensível: o Sklearn é bem otimizado e, por padrão, usa muitos parâmetros na árvore que não levamos em consideração), mas, ao adicionar valores, o resultado fica mais agradável.

Para resumir: aprendemos a escrever árvores decisivas do zero, aprendemos a melhorar seu desempenho e testamos sua eficácia em conjuntos de dados reais comparando-os com o algoritmo do Sklearn. No entanto, os métodos apresentados aqui não limitam a melhoria dos algoritmos, portanto, lembre-se de que o código proposto pode ser ainda melhor. No próximo artigo, escreveremos impulsionamentos com base nesses algoritmos.

Todo o sucesso!