Gravando o XGBoost a partir do zero - parte 2: aumento de gradiente

Olá pessoal!

No último artigo, descobrimos como as árvores de decisão são organizadas e, do zero, implementamos
algoritmo de construção, otimizando e melhorando simultaneamente. Neste artigo, implementaremos o algoritmo de aumento de gradiente e, no final, criaremos nosso próprio XGBoost. A narração seguirá o mesmo padrão: escrevemos um algoritmo, descrevemos e resumimos comparando os resultados do trabalho com análogos do Sklearn.

Neste artigo, a ênfase também será colocada na implementação em código; portanto, é melhor ler toda a teoria juntos em outra (por exemplo, no curso ODS ) e, já com o conhecimento da teoria, você pode prosseguir para este artigo, pois o tópico é bastante complicado.



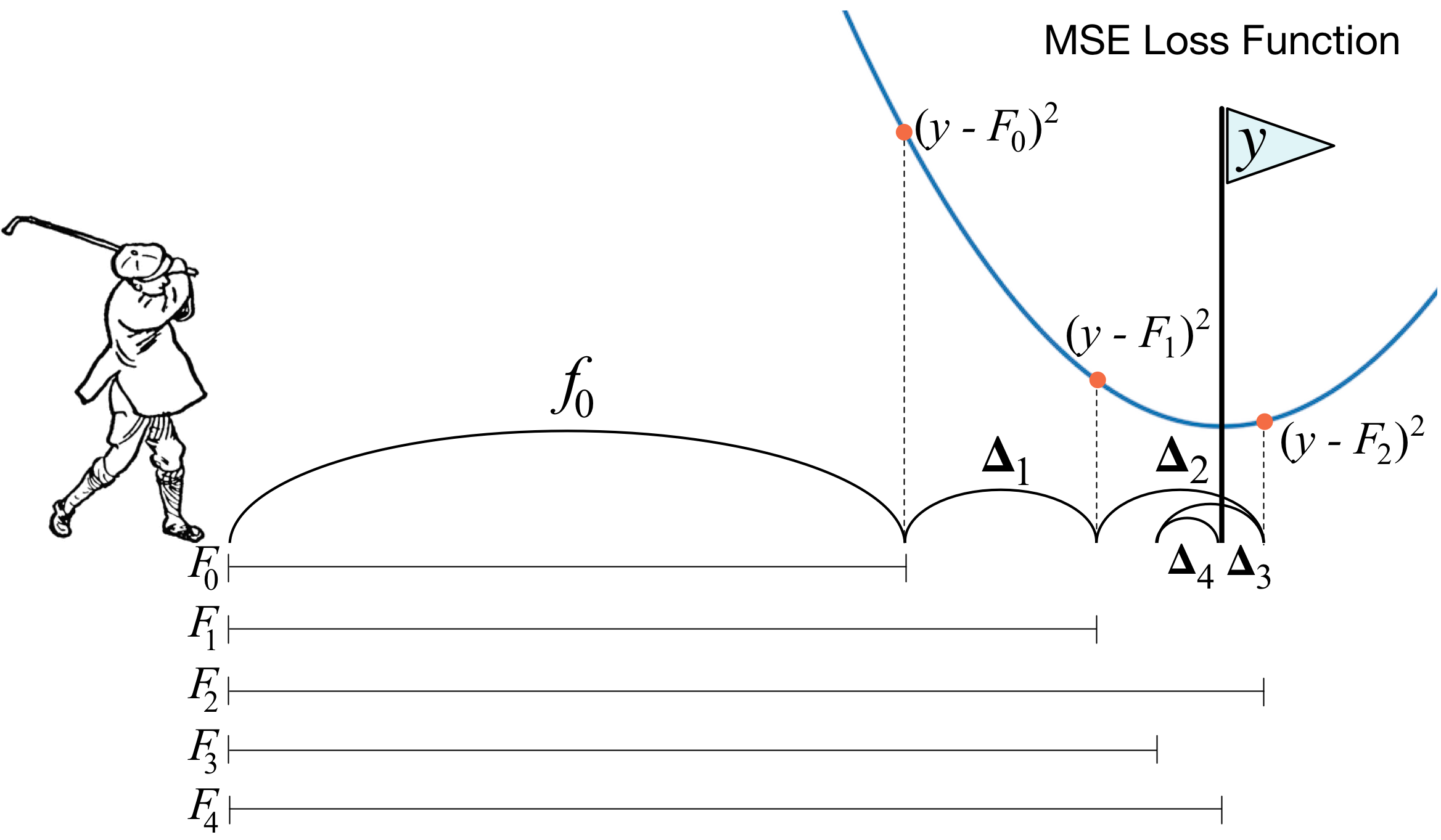
O que é aumento de gradiente? A imagem de um jogador de golfe descreve perfeitamente a idéia principal. Para empurrar a bola para dentro do buraco, o jogador de golfe faz cada próximo golpe levando em consideração a experiência de tacadas anteriores - para ele, essa é uma condição necessária para colocar a bola no buraco. Se for muito rude (não sou mestre em golfe :)), a cada novo golpe, a primeira coisa que um jogador observa é a distância entre a bola e o buraco após o golpe anterior. E a principal tarefa é reduzir essa distância com o próximo golpe.

O impulso é construído de maneira muito semelhante. Primeiro, precisamos introduzir a definição de "buraco", ou seja, a meta pela qual lutaremos. Em segundo lugar, precisamos aprender a entender de que lado precisamos vencer com um clube para nos aproximarmos do objetivo. Em terceiro lugar, levando em consideração todas essas regras, é necessário criar a seqüência correta de tacadas para que cada uma delas subseqüente reduza a distância entre a bola e o buraco.

Agora, damos uma definição um pouco mais rigorosa. Introduzimos o modelo de votação ponderada:

$$

$$h (x) = \ sum_ {i = 1} ^ nb_ia_i, x \ em X, b_i \ em R$$

Aqui $$$X$ É o espaço do qual tiramos objetos, $$$b_i, a_i$ - este é o coeficiente na frente do modelo e o próprio modelo, ou seja, a árvore de decisão. Suponha que já em alguma etapa, usando as regras descritas, fosse possível adicionar à composição $$$T-1$ algoritmo fraco. Para aprender a entender que tipo de algoritmo deve estar na etapa $$$T$ , apresentamos a função de erro:

$$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) \ rightarrow min_ {a_T, b_T}$

Acontece que o melhor algoritmo será aquele que pode minimizar o erro recebido nas iterações anteriores. E como o aumento é gradiente, essa função de erro deve necessariamente ter um vetor antigradiente ao longo do qual você pode se mover em busca de um mínimo. Isso é tudo!

Imediatamente antes da implementação, adicionarei algumas palavras sobre como tudo será organizado conosco. Como no artigo anterior, tomamos o MSE como uma perda. Vamos calcular seu gradiente:

$$

$$mse (y, prever) = (y - prever) ^ 2 \\ \ nabla_ {prever} mse (y, prever) = prever - y$$

Assim, o vetor antigradiente será igual a $$$y - prever$ . Na etapa $$$i$ consideramos os erros do algoritmo obtido em iterações anteriores. Em seguida, treinamos nosso novo algoritmo nesses erros e o adicionamos ao nosso conjunto com um sinal de menos e algum coeficiente.

Agora vamos começar.

1. Implementação da classe usual de aumento de gradiente

import pandas as pd import matplotlib.pyplot as plt import numpy as np from tqdm import tqdm_notebook from sklearn import datasets from sklearn.metrics import mean_squared_error as mse from sklearn.tree import DecisionTreeRegressor import itertools %matplotlib inline %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeFastMse: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeFastMse left cpdef RegressionTreeFastMse right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #   -   y self.value = y.mean() #   - mse     base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -  ,  ,    delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeFastMse(self.max_depth - 1) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree def fit(self, X, y): self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: #    resid = (y - prediction) #    if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth, min_size = self.min_size) if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth, min_size = self.min_size) #     tree.fit(X, resid) #        b = tree.predict(X).reshape([X.shape[0]]) self.trees_.append(tree) prediction += self.learning_rate * b #       if t > 0: self.loss_by_iter.append(mse(y,prediction)) return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

Agora, construiremos a curva de perda no conjunto de treinamento para garantir que a cada iteração realmente tenhamos uma diminuição.

 GDB = GradientBoosting(n_estimators=50) GDB.fit(X,y) x = GDB.predict(X) plt.grid() plt.title('Loss by iterations') plt.plot(GDB.loss_by_iter) 

2. Ensacamento sobre árvores decisivas

Bem, antes de compararmos os resultados, vamos falar sobre o procedimento de empacotar árvores.

Tudo é simples aqui: queremos nos proteger da reciclagem e, portanto, com a ajuda da amostragem com retorno, calcularemos a média de nossas previsões para não gerar emissões acidentalmente (por que isso funciona - leia melhor o link).

 class Bagging(): '''  Bagging -      . ''' def __init__(self, max_depth = 3, min_size=10, n_samples = 10): #super(CART, self).__init__() self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): #      indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): #    self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): #        num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

Bem, agora como algoritmo básico, podemos usar não apenas uma árvore, mas ensacá-las - então, novamente, nos protegeremos da reciclagem.

3. Resultados

Compare os resultados dos nossos algoritmos.

 from sklearn.model_selection import KFold import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn import copy def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in tqdm_notebook(kf.split(X)): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' )) er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' )) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1)) %matplotlib inline data = [er_sklearn_boosting, er_boosting, er_boobagg] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag']) plt.grid() plt.show() 

Recebido:



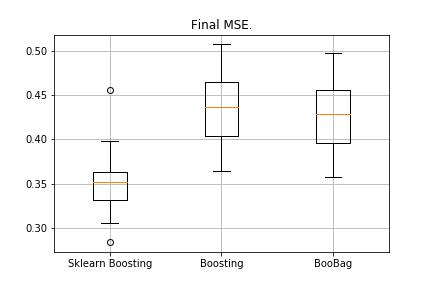
Ainda não podemos derrotar o analógico do Sklearn, porque novamente não levamos em consideração muitos parâmetros usados neste método . No entanto, vemos que o ensacamento ajuda um pouco.

Não vamos nos desesperar e passar a escrever o XGBoost.

4. XGBoost

Antes de ler mais, recomendo fortemente que você se familiarize com o próximo vídeo , o que explica muito bem a teoria.

Lembre-se de qual erro minimizamos no impulso normal:

$$

$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j))$$

O XGBoost adiciona explicitamente regularização a esta funcionalidade de erro:

$$

$$err (h) = \ sum_ {j = 1} ^ NL (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) + \ sum_ {i = 1} ^ T \ ômega (a_i)$$

Como considerar essa funcionalidade? Primeiro, nós o aproximamos com a ajuda de uma série de Taylor de segunda ordem, onde o novo algoritmo é considerado como um incremento ao longo do qual iremos mover e, em seguida, já pintamos dependendo do tipo de perda que temos:

$$$f (x + \ delta x) \ thickapprox f (x) + f (x) '\ delta x + 0,5 * f (x)' '(\ delta x) ^$

É necessário determinar qual árvore consideraremos ruim e qual é boa.

Lembre-se de que princípio a regressão é construída com $$$L_2$ -regularização - quanto mais normais os valores dos coeficientes antes da regressão, pior é, portanto, necessário que sejam tão pequenos quanto possível.

No XGBoost, a idéia é muito semelhante: a árvore é multada se a soma da norma dos valores nas folhas for muito grande. Portanto, a complexidade da árvore é apresentada da seguinte maneira:

$$

$$\ omega (a) = \ gama Z + 0,5 * \ sum_ {i = 1} ^ {Z} w_i ^ 2$$

$$$w$ - valores nas folhas, $$$Z$ - número de folhas.

Existem fórmulas de transição no vídeo, não as exibiremos aqui. Tudo se resume ao fato de escolhermos uma nova partição, maximizando o ganho:

$$

$$Gain = \ frac {G_l ^ 2} {S_l ^ 2 + \ lambda} + \ frac {G_r ^ 2} {S_r ^ 2 + \ lambda} - \ frac {(G_l + G_r) ^ 2} {S_l ^ 2 + S_r ^ 2 + \ lambda} - \ gamma$$

Aqui $$$\ gama, \ lambda$ Os parâmetros numéricos de regularização e $$$G_i, S_i$ - as somas correspondentes da primeira e segunda derivadas para esta partição.

É isso, a teoria é bem resumida, os links são dados, agora vamos falar sobre quais serão os derivados se trabalharmos com o MSE. É simples:

$$$mse (y, prever) = (y - prever) ^ 2 \\ \ nabla_ {prever} mse (y, prever) = prever - y \\ \ nabla_ {prever} ^ 2 mse (y, prever) = 1$

Quando vamos calcular a quantidade $$$G_i, S_i$ , basta adicionar ao primeiro $$$prever - y$ e o segundo é apenas a quantidade.

 %%cython -a import numpy as np cimport numpy as np cdef class RegressionTreeGain: cdef public int max_depth cdef public np.float64_t gain cdef public np.float64_t lmd cdef public np.float64_t gmm cdef public int feature_idx cdef public int min_size cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef public RegressionTreeGain left cpdef public RegressionTreeGain right def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5): self.max_depth = max_depth self.gmm = gmm self.lmd = lmd self.left = None self.right = None self.feature_idx = -1 self.feature_threshold = 0 self.value = -1e9 self.min_size = min_size return def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef long idx = 0 cpdef long thres = 0 cpdef np.float64_t gl, gr, gn cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 cpdef np.float64_t best_gain = -self.gmm if self.value == -1e9: self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 if self.max_depth <= 1: return dim_shape = X.shape[1] left_value = 0 right_value = 0 #    # -  -   mse, L = (y - pred)**2 # dL/dpred = pred - y,          - # dL^2/d^2pred = 1 - ,       for feat in range(dim_shape): idxs = np.argsort(X[:, feat]) gl,gr = y.sum(),0.0 N1, N2, thres = N, 0, 0 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] gl -= y[idx] gr += y[idx] #   gn = (gl**2) / (N1 + self.lmd) + (gr**2) / (N2 + self.lmd) gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue #     if (gn > best_gain) and (min(N1,N2) > self.min_size): flag = 1 best_gain = gn left_value = -gl / (N1 + self.lmd) right_value = -gr / (N2 + self.lmd) self.feature_idx = feat self.feature_threshold = x thres += 1 self.gain = best_gain if self.feature_idx == -1: return self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.left.value = left_value self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) #    if (self.left.left == None or self.right.left == None): if self.gain < 0.0: self.left = None self.right = None self.feature_idx = -1 def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Um pequeno esclarecimento: para tornar as fórmulas nas árvores com ganho mais bonitas, treinamos o alvo com um sinal de menos.

Modificamos levemente nosso impulso, adaptamos alguns parâmetros. Por exemplo, se notarmos que a perda começou a atingir um platô, diminuímos a taxa de aprendizado e aumentamos max_depth para os estimadores a seguir. Também adicionaremos uma nova ensacadeira - agora aumentaremos sobre as ensacadas das árvores com ganho:

 class Bagging(): def __init__(self, max_depth = 3, min_size=5, n_samples = 10): self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree #  -       #   ,   lr   max_depth self.add_to_max_depth = 1 self.init_mse_board = 1.5 def fit(self, X, y): print (self.base_tree) self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: resid = (y - prediction) if (mse(temp_resid,resid) < self.init_mse_board): self.init_mse_board /= 1.5 self.add_to_max_depth += 1 self.learning_rate /= 1.1 # print ('Alert!', t, self.add_to_max_depth) if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) if self.base_tree == 'XGBoost': tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid tree.fit(X, resid) b = tree.predict(X).reshape([X.shape[0]]) # print (b.shape) self.trees_.append(tree) prediction += self.learning_rate * b temp_resid = resid return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

5. Resultados

Por tradição, comparamos os resultados:

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging')) er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost')) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2)) %matplotlib inline data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost', 'XGBooBag']) plt.grid() plt.show() 

A imagem será a seguinte:



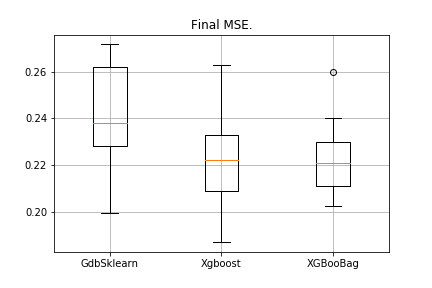
O XGBoost tem o erro mais baixo, mas o XGBooBag tem um erro mais cheio, o que é definitivamente melhor: o algoritmo é mais estável.

Isso é tudo. Eu realmente espero que o material apresentado em dois artigos seja útil e que você possa aprender algo novo por si mesmo. Agradeço especialmente a Dmitry pelo feedback abrangente e pelo código-fonte, a Anton pelo conselho e a Vladimir pelas tarefas difíceis de estudar.

Todo o sucesso!