Explicação da natureza física do fenômeno "Lift Force" sem usar a equação de Bernoulli

Monin Ilya Alekseevich, candidato a ciências técnicas MSTU em homenagem a Bauman., SM-9, imoninpgd@gmail.com

Crítica da Explicação Teórica existente de Lift na asa de um avião

Depois de ouvir um curso no Instituto de Física e Tecnologia de Moscou, Faculdade de Aeromecânica e Engenharia de Aeronaves (FALT) “Introdução à Aerodinâmica” e ler vários estudantes universitários diferentes sobre “Aerodinâmica” [1-3], fiquei intrigado com várias contradições óbvias nas explicações da física do fluxo ao redor de um ar (gás ou ideal líquidos) de vários objetos sólidos e a formação de sustentação na asa.

1. A versão principal da formação de sustentação da asa circulada pela Versão é a diferença nas velocidades do fluxo de ar (líquido) acima da asa e sob a asa e, como resultado, ocorre uma queda de pressão de acordo com a Lei de Bernoulli. Nesse caso, através da lei de Bernoulli, a velocidade calculada do fluxo na superfície da asa é inequivocamente associada à pressão instrumentalmente registrada na asa, ignorando outras explicações possíveis baseadas em leis não menos básicas da física.
2. Na análise do fluxo em torno dos perfis de um líquido invíscido ideal em fluxos planos, foi obtido um aumento surpreendentemente grande nas taxas de fluxo em comparação com a velocidade base V0. Ou seja, a lei de conservação de energia é refutada, uma vez que a energia é retirada do nada para acelerar o fluxo, excedendo a energia do fluxo incidente na asa. Ao mesmo tempo, o postulado da hidrodinâmica é ignorado, o que, de acordo com a mesma lei de Bernoulli, quando o jato expira abaixo do nível, o cabeçote de velocidade é exclusivamente limitado de cima pela pressão estática no navio, ou seja, o cabeçote de velocidade do jato após a aceleração na asa não pode exceder a pressão estática comprimida durante a frenagem do meio.

Para o vôo de uma aeronave moderna, a força de elevação necessária de 500-600kg / m.sq. Ao decolar e pousar, a velocidade das aeronaves modernas é de cerca de 250 km / h. Nesse caso, a força de elevação necessária na asa é fornecida a uma velocidade de fluxo do plano superior da ordem de 450 km / h.

Qual é o mecanismo dessa aceleração do fluxo de ar sem um mecanismo visível de aceleração?

De fato, o contato da asa com o fluxo que se aproxima apenas pode levar à desaceleração do fluxo, mas não à sua aceleração!

Essas contradições devem ser removidas!

A física não deve perder seu significado físico em prol de belas e complexas construções matemáticas!

Vamos considerar outra explicação para a formação da força de elevação da asa sem violações reveladas das leis da física e do senso comum. Isso exigirá a aplicação das leis da mecânica comum.

Em consideração, consideramos que o ar consiste em partículas individuais (repulsivas mutuamente (para criar pressão de gás)) com sua própria massa, cada uma das quais obedece às leis da mecânica quando sua direção e velocidade são alteradas.

A ambiguidade da relação de rarefação sobre a asa com um aumento da vazão

A asa real em consideração não é um elemento de um tubo ideal no modelo da Lei de Bernoulli, mas é um objeto sólido limitado no espaço ilimitado de um gás real em movimento, consistindo em partículas de gás bastante tangíveis em massa e tamanho. Nesse caso, deve-se considerar o fluxo curvo dos jatos sobre a superfície curva da asa, levando em consideração as forças de inércia e a pressão gerada, perpendiculares ao vetor de velocidade e à superfície da asa.

Se considerarmos o movimento dos jatos sobre o perfil da asa, um fluxo de ar pode criar um vácuo sobre a asa devido à curvatura de seu fluxo.

Portanto, para dobrar o movimento retilíneo do corpo, você precisa aplicar força na direção perpendicular ao vetor de velocidade. No caso de um fluxo plano contínuo, por sua curvatura, é necessário garantir a diferença de pressão acima e abaixo dela. Ao mesmo tempo, haverá aumento da pressão no lado convexo do jato e pressão reduzida no lado côncavo.
Ao se mover pela circunferência de um ponto material, a aceleração centrípeta será criada pela força

F = m * V ^ 2 / R

E com o mesmo movimento circular de uma fina camada gasosa de espessura dR, a massa será igual a

m = q * S * dR ,

onde S é a área da camada de gás, q é a densidade do gás. Se você levar a força centrípeta para a área elementar da camada de gás, a força se transformará em pressão

P = q * V ^ 2 * dR / R

Quando um fluxo de ar flui sobre a superfície da asa, a camada de gás se move ao longo de um caminho curvo. Cada ponto dessa trajetória tem seu próprio raio de curvatura, o que nos permite calcular a pressão do gás inercial na direção perpendicular à velocidade.

Assim, é possível calcular diretamente a pressão (vácuo) na asa a partir da camada de gás que flui acima de sua superfície, e a velocidade do fluxo de gás sempre será assumida como sendo igual à velocidade da asa Vo.

Para começar, consideramos o caso mais simples de uma asa na forma de uma placa de espessura zero dobrada com um raio R. Tais perfis curvos finos são usados ​​para planadores ultraleves na modelagem de aeronaves.

A propósito, de acordo com a teoria usual da lei de Bernoulli, uma placa curva fina não deve ter força de elevação, uma vez que o comprimento do caminho sob a asa e acima da asa é o mesmo. Mas a asa fina tem sustentação, e é muito significativa, o que mostra claramente a incorreta do modelo de sustentação usando a lei de Bernoulli.

Para o cálculo estimado da asa, escolheremos a altura do perfil usual para aviões de baixa velocidade, 20% da largura da asa. Nesse caso, para a altura do perfil, fazemos a diferença nas alturas das arestas de ataque e de fuga em relação ao fluxo de ar horizontal (veja a Figura 1-3)


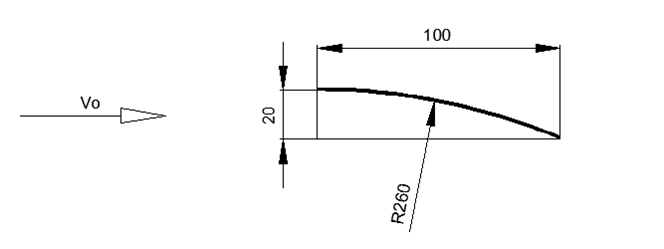Fig. 1. Geometria fina da asa de curvatura constante


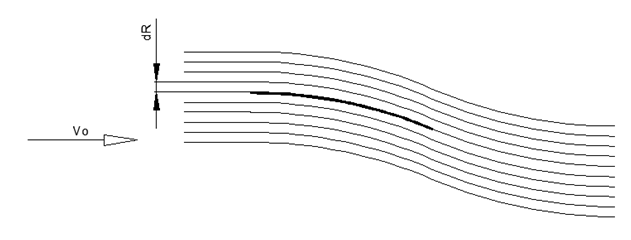Fig. 2. Fluxo estimado em torno de uma asa de raio fino


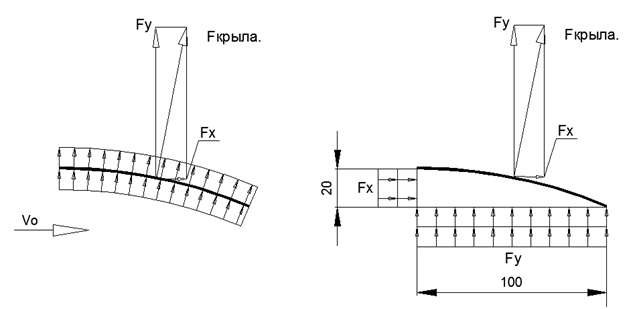Fig. 3. A natureza da distribuição da pressão sobre uma asa de raio fino e as forças resultantes nas direções

Então, com uma largura de 1 me 20% de altura do perfil, o raio da asa será de 2,6 m, desde que a tangente à asa seja horizontal na parte superior do perfil.

Agora calculamos a pressão centrípeta na asa a partir da camada de ar curvada ao longo do arco.

Portanto, para uma velocidade de 70 m / s (252 km / h), a pressão de uma camada com uma espessura de 0,1 m com um raio de curvatura de 2,6 m é 235,6 Pa ou 24 kg / m.sq. e a velocidade da cabeça em 70 m / s é 3063 Pa.

Dado que uma asa fina flui de dois lados, esses valores devem ser pelo menos dobrados e multiplicados por um certo número de camadas paralelas, também curvas pela asa em movimento. Se assumirmos que a espessura da camada perturbada não é inferior à metade da largura da asa em cada lado da asa, obteremos a carga dez vezes maior na asa de cerca de 2356 Pa. Esses números superam os valores de carga da asa para aeronaves de motores leves de baixa velocidade com uma asa espessa e uma curvatura similar da superfície da asa. (ver tabela 1)

Como a pressão Pcr é aplicada à superfície curva da placa fina, a força Fcr de Pcr pode ser decomposta na força de elevação Fy e na resistência ao voo Fx.
A força de elevação Fy é igual à integral da projeção no eixo Y das forças da pressão do fluxo Curvilíneo Pcr sobre toda a área da asa.

No caso de pressão uniforme na asa circular, o valor de Fy será igual ao produto Pcr pela área de projeção da asa pelo eixo X, que é igual a S = B * L da asa (neste caso, 1 m² / mp).

Fy = Pkr * Bkr = 2356 * 1 = 2356 N / p.

Ao mesmo tempo, a resistência ao movimento horizontal nesse caso será igual à integral de projeção dFcr no eixo X sobre toda a área da asa. No caso de pressão uniforme na asa, o valor de Fx será igual ao produto Pcr pela área de projeção da asa no eixo Y, que é igual à altura H do perfil da asa (neste caso, 0,2 m² / mp).

Fx = Pkr * Nkr = 2356 * 0,2 = 462 N / p.

Nesse caso, obtemos K = Fy / Fx = (Pkr * Vkr) / (Pkr * Nkr) = Bkr / Nkr, ou seja, com pressão uniforme em um perfil fino circular, a qualidade da asa é igual à razão apenas dos parâmetros geométricos do perfil K = B / N.

De acordo com a regra da expansão vetorial de forças de uma determinada figura, é possível obter imediatamente o valor da qualidade da asa K = Fy / Fx, que neste caso é igual a K = 100 * Pkr / 20 * Pkr = 5.

É interessante que, se você dimensionar essa asa de design em uma diminuição de dez vezes (ao longo do raio de curvatura, altura e largura do perfil), a pressão na asa permanecerá inalterada em velocidades de vôo iguais (consulte a tabela 2). É por esse motivo que os pesados ​​mísseis de cruzeiro voam com asas bastante pequenas e finas. Acontece que suas asas pequenas e finas com curvatura suficiente são realmente suficientes para criar a força de elevação necessária!

Como a modelagem de sala é barata o suficiente, esses números são verificados com simplicidade em modelos em escala real.

Tab. 1. A pressão das camadas de ar curvas em uma asa de raio constante R = 2,6 m, dependendo da velocidade do vôo.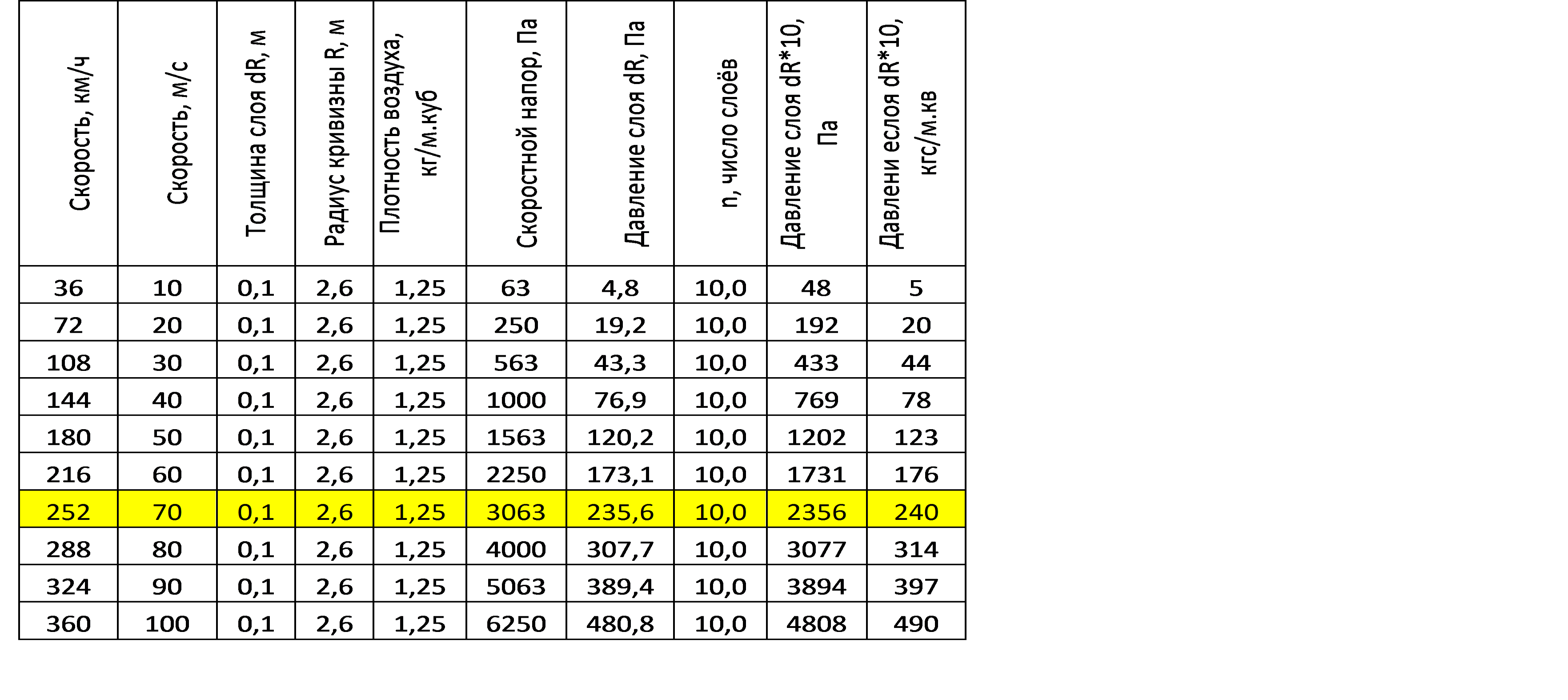



Tab. 2. A pressão das camadas de ar curvas na asa de raio constante R = 0,26 m, dependendo da velocidade do vôo.



É interessante considerar como a asa Kkr muda com sua curvatura constante Rkr, mas com um parâmetro de largura de perfil variável Vkr. (Ver tabela 3)

Na primeira linha da tabela, a qualidade aerodinâmica da asa atinge um valor fantástico de K = 182, mas a carga na asa é de apenas 67 Pa (7 kgf / m.sq.), o que é adequado apenas para modelos de aeronave de planadores de dimensão ambiente.

A força de elevação necessária na asa surge apenas em asas K suficientemente pequenas, que podem ser vistas nas últimas linhas da mesa.

A coluna do parâmetro variável e a linha do perfil inicial com Kkr = 5 são destacadas em amarelo.

Tab. 3. Alteração dos parâmetros de uma asa de raio constante R = 2,6 m em diferentes ângulos de perfil (largura do perfil) a uma velocidade de vôo constante.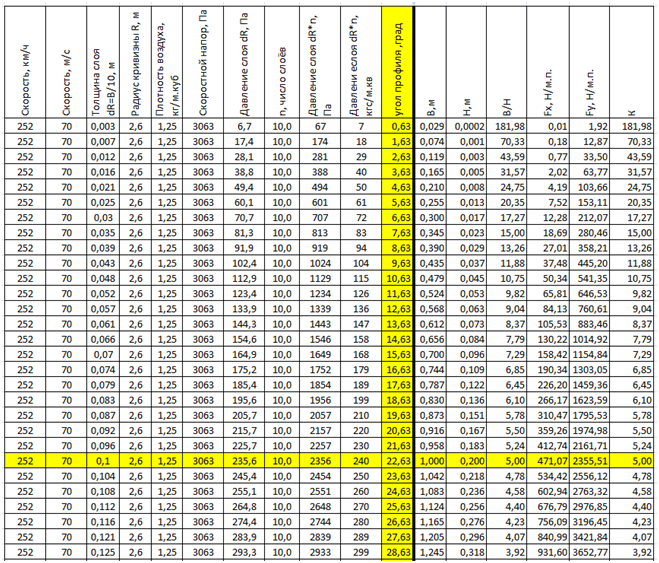



Você também pode calcular a alteração na força de elevação Fy e a qualidade da asa Kkr para a asa com um acorde constante, mas com diferentes curvaturas da asa a uma velocidade constante. As colunas destacadas em amarelo são: Argumento variável Rcr - raio de curvatura e largura constante do perfil Vcr. A linha do perfil inicial com Kkr = 5 também é destacada.

Tab. 4. Alteração dos parâmetros de uma asa com raio de curvatura variável a uma largura de perfil constante B = 1 m a uma velocidade de vôo constante.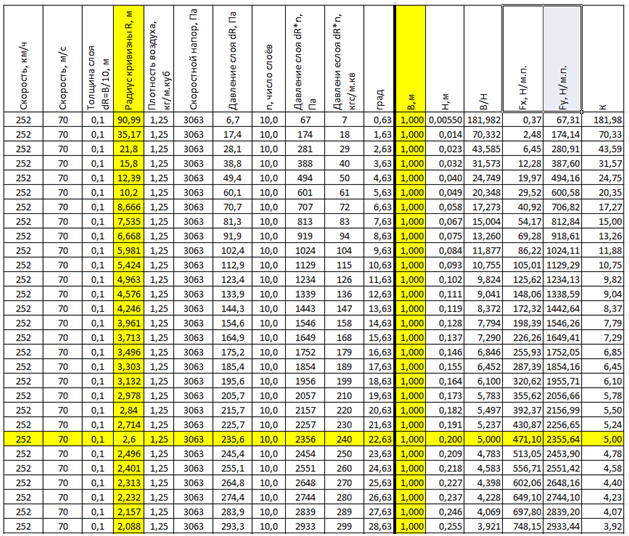



No modelo descrito, para obter um vácuo acima da asa, não é necessária uma aceleração adicional do ar acima da asa. Uma descarga notável acima da asa é garantida sob condições de curvatura significativa do fluxo de ar ao redor da asa, sob a influência de forças estáticas de pressão do ar em todo o espaço circundante. O ângulo de inclinação do acorde da placa curva inicial é de 11,3 graus (metade do ângulo do segmento do arco é 22,6 graus), o que está de acordo com os modos de aterrissagem da asa dos aviões modernos durante o pouso com a mecanização da asa liberada (ripas + abas). No modo de aterrissagem, a asa com a mecanização liberada lembra muito mais o caso considerado de uma chapa fina curva do que a asa clássica com um plano inferior reto (veja a figura 4).



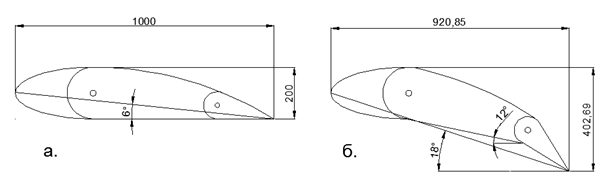Fig. 4. Asa assimétrica com superfície plana e aerodinâmica inferior: a) posição reta para vôo em alta velocidade; b) asa com curvatura máxima com mecanização totalmente liberada.

A asa fina fortemente curvada é amplamente utilizada como pás do ventilador. As baixas velocidades lineares com valores de baixa pressão permitem o uso de chapas finas de aço ou plástico de espessura extremamente pequena como ventiladores nos ventiladores, pois sua força é suficiente para suportar as cargas existentes.

Em aeronaves pesadas, o uso de asas finas é tecnicamente impossível por causa de sua força insuficiente. A grande espessura da asa permite colocar dentro da asa vigas de sustentação de carga bastante altas, com força e rigidez suficientes para flexão e torção, mantendo um peso aceitável para a aeronave. É por esse motivo que toda a aerodinâmica estuda asas com espessura bastante tangível. Por esse motivo, passamos de considerar a aerodinâmica de uma placa fina e curva para o perfil da asa com espessura real e planos de diferentes curvaturas.

Ao final da consideração do modelo de fluxo em torno de uma asa fina, é necessário dar mais uma prova da operacionalidade do modelo proposto para a explicação da “força de elevação da asa”. Como é conhecido da mecânica, Força é a mudança no momento por unidade de tempo, ou seja,

F = d (m * V) / dT

No modelo sonoro do fluxo em torno de uma asa fina e curva, podemos calcular a força de elevação Fy como a mudança vertical no momento do fluxo de ar de entrada, considerado como

Fy2 = (dR * 10 * q * Vo) * Vo * sinAcr ,

Onde Vo é a velocidade da asa, dR é a espessura da camada curva elementar do fluxo de ar no modelo de cálculo, 10 é o número de camadas a serem curvadas ao mesmo tempo e Acr é o ângulo de descida do fluxo da asa até a direção da velocidade inicial Vo.

Depois de feito o cálculo, obtemos que ambos os cálculos dão o mesmo resultado.

Ou de forma analítica:

Fy1 = Pcr * Bcr ,

Pkr = (dR * 10 * q * Vo) * Vo / R ,

Bcr = R * sinAcr

Substituindo o desenvolvimento Pkr e Bkr na expressão para Fy1 e reduzindo o mesmo nome R no numerador e denominador, obtemos:

Fy = Pkr * Bkr = (dR * 10 * q * Vo) * Vo * sinAcr

Portanto, a igualdade Fy = Fy1 = Fy2 é sempre verdadeira

Ou seja, o método "Inercial-curvilíneo" para calcular a "Força de sustentação" de uma asa fornece uma fórmula idêntica à do método "Força de pulso reativo" para uma asa da mesma geometria.
Isso significa que os aviões voam não devido a algum tipo de força "mágica" dos "vórtices mágicos", mas devido ao antigo e compreensível "impulso de força" ou "impulso de jato" ao lançar uma massa de ar.

Asa gorda

Em baixas velocidades de vôo durante a decolagem e aterrissagem (M = 0,2 ou 250 km / h), a cabeça de pressão não excede 3 kPa (3% da pressão atmosférica ao nível do mar de 100 kPa), ou seja, é tão pequena em relação à pressão atmosférica básica que a compressão geométrica do fluxo se torna visualmente indetectável ao desenhar um jato perto da asa.

Para criar elevação acima da asa, é necessário criar uma curvatura do fluxo para que a asa fique na zona côncava do fluxo de ar. Assegurar essa curvatura do jato acima da asa ajuda a curvatura do plano superior da asa, localizado na sombra aerodinâmica da carenagem do nariz da asa.

Ao mesmo tempo, o plano inferior da asa flui em linha reta, sem criar vácuo ou em uma superfície côncava, descartando o fluxo de ar para baixo, o que cria um aumento positivo da pressão na asa por baixo e é combinado com a força de elevação do vácuo acima da asa.
A principal diferença entre uma asa grossa e uma placa fina no nosso caso será a aparência de uma carenagem frontal, espalhando o fluxo de ar que se aproxima antes que ele atinja planos curvos que criam sustentação.

Uma zona de frenagem surge em frente à asa espessa voadora, onde a velocidade do ar se torna igual a zero (em relação à asa), e a sobrepressão nessa zona é igual à cabeça de pressão Pvo.

Não será possível desenhar linhas de fluxo sem levar em consideração a compressão do ar; caso contrário, será necessário aceitar a versão da aceleração do ar acima da superfície da asa ou a zona de influência com uma curva de fluxo avançará ao infinito em um meio incompressível, o que é implausível.
A propósito, ambos os efeitos (aceleração do fluxo e a infinita zona de influência em líquidos incompressíveis) se manifestam na prática em túneis de vento com linhas de corrente de fumaça e quando os submarinos se movem em profundidades rasas.

Assim, nos túneis de vento (ADT), o fluxo ao redor dos modelos testados ocorre com uma aceleração perceptível do fluxo (redução na espessura das linhas de fumaça) na abertura da parede do modelo ADT. Isso é apenas a interpretação desse fenômeno que é completamente incorretamente atribuída à aceleração do fluxo para a formação da força de elevação. De fato, a aceleração do fluxo no espaço "parede do modelo ADT" é simplesmente uma conseqüência do estreitamento do furo no caminho do fluxo do ADT, mantendo um fluxo de ar constante no próprio ADT devido a ventiladores potentes com uma característica de ventilador rígida.

Quando os submarinos se movem em profundidades rasas acima do submarino, forma-se uma corcova visualmente visível. O valor dessa corcunda é igual ao volume de água na frente do casco do submarino, que de alguma forma deve ser movido da zona em frente ao submarino para a zona da popa ao se mover em uma determinada velocidade. Uma corcova na superfície também é formada quando o submarino se move a grandes profundidades, mas devido à maior área de expansão da corcunda, sua altura se torna indetectável com uma simples observação visual. A causa do hump de água na superfície é explicada pela incapacidade de mover o líquido incompressível em direção ao fundo, e em direção à superfície uma fina camada de água sob pressão atmosférica torna-se facilmente polarizada, com uma característica elástica clara da fonte de pressão e gravidade atmosféricas. A propósito, mesmo com o movimento de submarinos em grandes profundidades, um pedaço de água (e o próprio submarino como resultado) pode ser detectado pela observação de satélites usando equipamento altamente sensível que pode medir a geometria da superfície dos mares com grande precisão e isolar o pedaço de água do submarino do barulho das ondas na superfície. usando computadores.

Assim, consideramos o gás compressível e definimos a zona de influência do envelope da asa para depender da taxa de compressão do jato na pressão Pvo.

A pressão na zona de frenagem na carenagem é mantida por jatos curvos de ar que envolvem a carenagem. A relação da pressão com a curvatura das camadas de ar é a mesma que no caso de uma asa curva fina dP = q * Vo ^ 2 * dR / Rsl.

A magnitude da zona de influência, onde a curvatura do fluxo é perceptível, também está associada à magnitude de Vkr e Nkr. , , () .

, /2=R.

, vo , /2= R.
Pr= vo.



qVo^2*R/R= qVo^2/2



R= 2* R

, , ( ), .

, . , . (..5).



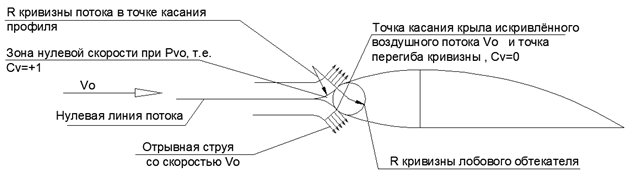.5. Vo .

Pvo , , , .

, . . (..6).

« » : « … , , ( ), …». .

, . - ( ) , , .

- ./. , «» (. .6).

, .



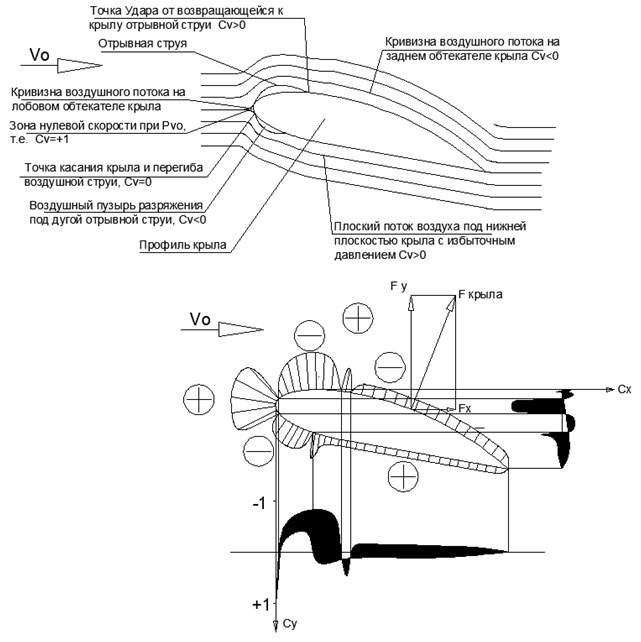.6. . . Y .

. . =1 , , , , . , ( ).
, . , Fy .

, «», , .

«» (..7). 4-5 (..1-2). «» , . , . .



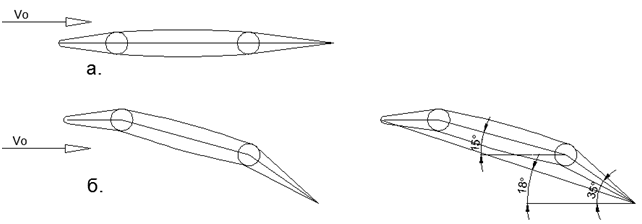.7. /=0,1 (10%) «» : ) ; ) .



.1. - 35 ( ).



.2. -29 - ( ).



.3. -29 .

(..3) «» : . , , . , . , , , , . -35 -57 , .

Na rede, você pode encontrar muito material explicativo sobre qualquer assunto, incluindo a formação de vórtices na asa de um avião, por exemplo:



Ao mesmo tempo, é fácil encontrar fotografias de traços de vórtice de aviões em camadas de nuvens na mesma Internet, que demonstram uma escala muito maior do fenômeno do que estão tentando mostrar em teoria.



Foto 4. Trilha de vórtice em uma camada de neblina atrás de um avião voando a uma altura. Os anéis do turbilhão de neblina visível estão a centenas de metros do avião, e a proximidade visual é uma ilusão de ótica criada por uma lente telefoto ao fotografar um avião a uma distância de vários quilômetros.



Foto 5. Trilha de vórtice em uma camada de neblina atrás de um avião voando a uma altura. Visível é um fluxo de ar vertical e as ondas de ar que vêm dos lados, torcidas em uma espiral em contato com um fluxo vertical descendente.



Foto 6. Trilha de vórtice em uma camada de névoa acima de uma pista atrás de um avião de pouso.

Esses enormes turbilhões emaranhados atrás dos aviões não são formados devido aos vórtices finais da asa. Os vórtices finais existem, é claro, mas seu papel não é tão grande e os projetistas de aeronaves estão lutando com sucesso.

Redemoinhos em larga escala a partir de fotografias são formados muito atrás do avião, quando uma onda de ar lançada pelo avião é substituída em dois lados pelo fluxo de ar sob a camada descendente para o espaço rarefeito por cima (veja a foto 4-5). Essa explicação da formação do vórtice satélite ecoa a questão já considerada da “zona de influência da asa no espaço circundante”. Nesse caso, o papel da superfície da Terra está no limite da distribuição do fluxo descendente do ar jogado pela asa para baixo. Ou seja, o voo da aeronave e a criação de "força de elevação da asa" também são possíveis na ausência de superfícies sólidas subjacentes, mas, ao mesmo tempo, o fluxo de ar jogado para baixo descerá infinitamente longo, perdendo velocidade e energia cinética à medida que se afasta, mas mantendo o momento vertical inalterado. A energia cinética da massa de ar descartada inicial será perdida com o envolvimento de fluxos de ar laterais no movimento, cuja multidirecionalidade simétrica não alterará o momento total inicial criado pela asa da aeronave. Uma ilustração clara do papel do limitador de terra é a foto 6. Lá, a corrente retilínea de neblina acima do airbus de aterrissagem (veja a foto 6) desce ao solo em uma linha reta e só então, bem atrás do avião, um deslocamento lateral começa ao longo do limitador de solo, e camadas de neblina dos lados e de cima já estão se aproximando no meio da camada de satélite, girando dupla espiral autocompensadora sobre o fluxo descendente.

"Efeito de tela" ao voar uma asa perto da Terra

À luz do papel declarado da Terra na formação da “Força de sustentação da asa”, faz sentido considerar adicionalmente o “Efeito Tela”, que sem a presença de uma superfície sólida da Terra não pode ocorrer. Assim, a física do vôo de asa no espaço aéreo infinito e no "Efeito Tela" perto da Terra tem uma natureza muito diferente.

Explicações do efeito Ekranoplan com base na compressibilidade do gás com baixo número de Mach

O efeito de uma superfície espaçada da Terra no levantamento de uma asa é chamado de "efeito de tela". Com esse efeito, a força de elevação da asa aumenta acentuadamente ao voar perto de uma superfície sólida (terra, água) a uma altura comparável ao tamanho do acorde da asa. Com base nesse efeito, mesmo toda uma classe de veículos voando baixo - WIG.

Qual é a essência do fenômeno? Esse problema pode ser resolvido apenas assumindo que o ar é um gás compressível.

Então, quando a asa voa acima do solo, um espaço de ar de tamanho limitado é formado entre duas superfícies sólidas. Quando uma asa está voando com um pequeno ângulo de ataque positivo, o fluxo de ar que se aproxima sob a asa experimenta uma compressão gradual da borda principal da asa até a borda traseira (veja a Fig. 8).

A pressão máxima de compressão na tela de fluxo sob a asa depende apenas da cabeça de velocidade em relação à asa voadora, e essa pressão na camada comprimida não pode exceder a pressão da cabeça de velocidade do ar:

Po = Vo ^ 2 * Q / 2 ,

onde está a pressão do ar da velocidade P na velocidade da asa V®, V® é a velocidade de vôo da asa, Q é a densidade do ar.

Conhecendo o incremento máximo de pressão sob a asa, calculamos os parâmetros geométricos no espaço da "almofada de ar".

Portanto, a uma velocidade de 40 m / s (144 km / h), a cabeça de velocidade Po = 1 kPa ou 1% de 1 atm. (100kPa).
Ou seja, a uma velocidade de 40 m / s, a pressão máxima sob a asa é alcançada por compressão de 1% na altura X da folga da borda principal da asa para a traseira. No olho, essa pré-carga é quase indetectável, e a camada sob a asa parece visualmente plana (ver fig. 8.a).

O ângulo de ataque será A = (Po / Ratm) * X / V radiano (em pequenos ângulos senA = A),
onde B é o acorde da asa, X é o espaço de ar no solo sob a asa no nível da borda de fuga da asa, R é a cabeça da velocidade do ar na velocidade da asa V® e Ratm é a pressão atmosférica (no nível do mar Ratm = 100 kPa).

Acontece que o ângulo máximo de ataque efetivo para obter um efeito de tela depende da altura da asa acima da superfície, da largura estrutural da asa e da velocidade de vôo especificada, e o ângulo de ataque é apenas uma derivada desses valores.

Conclusão: É possível aumentar a largura da asa quase infinitamente, reduzindo o ângulo de ataque para quase zero, atingindo a resistência mínima de Cx com o componente praticamente indutivo da resistência.

O “efeito de tela” em baixas velocidades de vôo fornece uma qualidade de asa muito alta, pois cria uma sustentação específica máxima na asa igual à cabeça de pressão Ro em ângulos de ataque extremamente pequenos em uma asa quase plana e muito fina. A qualidade da asa com baixos números de Mach durante o vôo na tela pode atingir K = 25-30.
A contribuição da rarefação sobre a superfície convexa superior da asa durante um vôo em uma “tela” com uma asa plana é bastante pequena em comparação com a pressão sob a asa.

Com o aumento da velocidade de vôo, o cabeçote de velocidade aumenta quadraticamente e, para obter o máximo efeito de tela, é necessário levantar o ângulo de ataque proporcionalmente ao aumento do cabeçote de velocidade Po.

Ou seja, aumentar a velocidade V0 para aumentar Po implica um aumento quadrático na velocidade do aumento no ângulo de ataque, o que, por sua vez, reduz drasticamente a qualidade da asa. E a partir de uma certa velocidade V®-max, a magnitude do efeito de tela com um grande ângulo de ataque é comparada com a força de elevação de um avião convencional no modo de pouso com mecanização estendida das asas.

Para qualquer ala com corda B, para aumentar a altitude de vôo X, é necessário levantar o ângulo de ataque, após o qual a WIG subirá para uma nova altura X2, onde o equilíbrio do grau de compressão do jato devido ao novo ângulo de ataque a uma nova altura será estabelecido novamente. Ao mesmo tempo, à medida que a altitude aumenta, o voo do ekranoplan começa a aumentar linearmente a resistência do voo, e a força de empuxo necessária correspondente também aumenta sem alterar a velocidade do vôo. Ou seja, a eficiência de combustível do voo de um ekranoplan pode mudar drasticamente de um aumento de altura de apenas alguns metros. Por exemplo, o alcance máximo de vôo do Oriole ekranolet a uma altitude de 0,8 m é de 1150 km, e a uma altitude de 0,3 metros com a mesma carga, já são 1480 km.



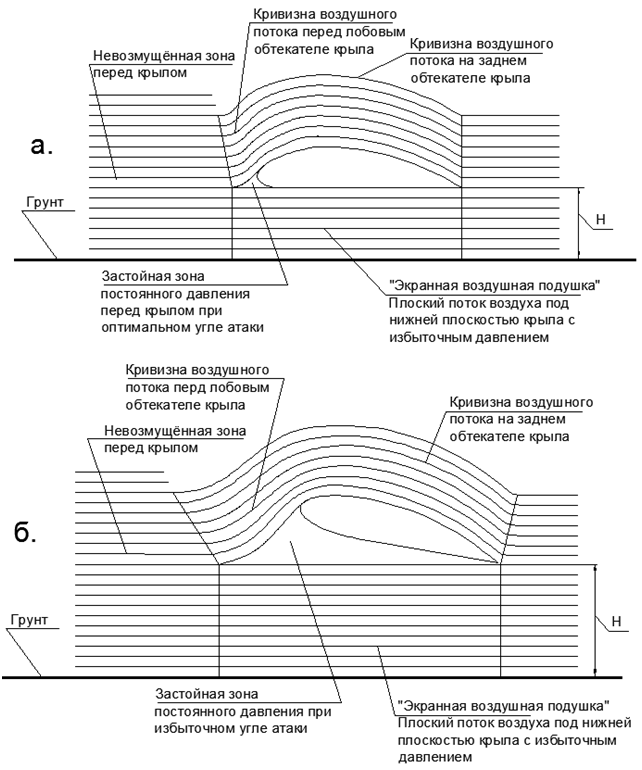Fig. 8. Configuração do fluxo de ar no "Efeito tela": a.) Ângulo de ataque ideal sem uma zona estagnada sob a asa, b) Ângulo excessivo de ataque formando uma grande bolha de ar estagnado de alta pressão entre a asa e a camada de ar comprimido da "almofada de ar da tela".

Conclusão: O rompimento adicional do ângulo de ataque da asa sem aumentar a velocidade de vôo na tela não aumenta a sustentação, mas apenas aumenta a resistência de vôo Cx (consulte a figura 8.b)

Considerando o ângulo da corda da asa do avião no modo de pouso de cerca de 15 graus, podemos estimar a quantidade de compressão do jato sob a asa à pressão Po e a velocidade correspondente V0, considerando o valor da corda B igual à altura da asa X.

15 graus corresponde a sin15 = 0,226

Em um ângulo de ataque de 15 graus, deve haver um cabeçote de pressão Po = 0,26 atm = 26 kPa, mas essas pressões são realizadas em velocidades muito altas (740 km / h) e excedem em muito as cargas de asa calculadas necessárias para o voo. Ou seja, um ângulo de ataque de pouso tão grande para criar um efeito de tela sobre a pista é excessivo a velocidades de pouso de 250 a 300 km / h.

A qualidade da asa em um ângulo de ataque de 15 graus cairá para um valor total de K = 3,7.
A velocidade de aterrissagem do avião é de apenas 250 km / h (70 m / s), enquanto a cabeça de pressão será Po = 3 kPa ou apenas 3% da Ratm, enquanto a carga normal da asa em vôo é de 5 kPa (500 kg / m.kv = 5% da Ratm). Ou seja, ao pousar, o efeito de tela do avião começa a ser notado sensivelmente pelo piloto a uma altura proporcional à largura da asa B, comparável à altura dos trens de pouso. Alinhar a aeronave e reduzir o ângulo de ataque a uma velocidade de 250 km / h permite que a aeronave penetre na “almofada de ar da tela”, pois sua capacidade de carga é menor que a pressão necessária sob a asa para o vôo.
Devido ao "efeito de tela", "Losslessness" ocorre em uma aeronave em vôo horizontal sem o lançamento da mecanização das asas em um ângulo de ataque de 5% (ou 3 graus) a uma pressão de Po = 5 kPa, que corresponde a Vo = 324 km / h ou 90 m / s.

Um ângulo de ataque de 5% (ou 3 graus) cria a qualidade de uma asa alada igual a K = 20.
Alto K = 30 corresponde a um ângulo de ataque de 3% (2 graus), enquanto a contrapressão sob a asa será de apenas 3% * Ratm = 3 kPa (300 kg / m.sq.), o que corresponde a uma cabeça de alta velocidade em V® = 70 m / s (250 km / h)

Assim, os modos de vôo com boa relação custo-benefício no modo “ekranoplan”, em comparação com o habitual “avião” de alta altitude, ficam na zona de baixa velocidade. Quando a qualidade da asa alada é menor que K = 20, é mais lucrativo usar aeronaves comuns de alta altitude para transporte. Ou seja, as áreas econômicas de operação das WIGs correspondem a velocidades abaixo de 300 km / h.

Manobra de peruca

Uma consideração separada é a questão de manobrar o WIG em voo. Como a força de elevação da asa na “tela” é formada diferentemente do que durante o vôo em grandes altitudes, ela não pode sequer manobrar “de avião”.

O ekranoplane não pode fazer curvas com um rolo na asa, pois receberá imediatamente uma perda de sustentação na asa elevada e o toque da água com a asa abaixada. Para o ekranoplan, a rotação é possível apenas com uma “panqueca”, ou seja, sem rolo, mas apenas criando forças laterais a partir da cauda vertical.

A cauda vertical da própria WIG também deve ser diferente da cauda do avião. A cauda vertical da WIG deve consistir em pelo menos duas quilhas, capazes de trabalhar de forma síncrona e aleatória, dependendo do tipo de manobra que está sendo realizada. A plumagem vertical, neste caso, não apenas realiza uma rotação WIG em torno de seu eixo vertical, mas também cria uma força horizontal na direção da velocidade de vôo.
A plumagem horizontal na quilha traseira controla o ângulo de ataque.
A asa larga e curta deve estar equipada com arruelas-terminais desenvolvidas para impedir que o fluxo comprimido sob a asa se espalhe para os lados. Além disso, essas arruelas skeg servem como pontões de aterrissagem para respingos.

Além disso, é necessária uma plumagem horizontal adicional nas extremidades da asa principal para compensar o momento de capotamento da ação da plumagem vertical.

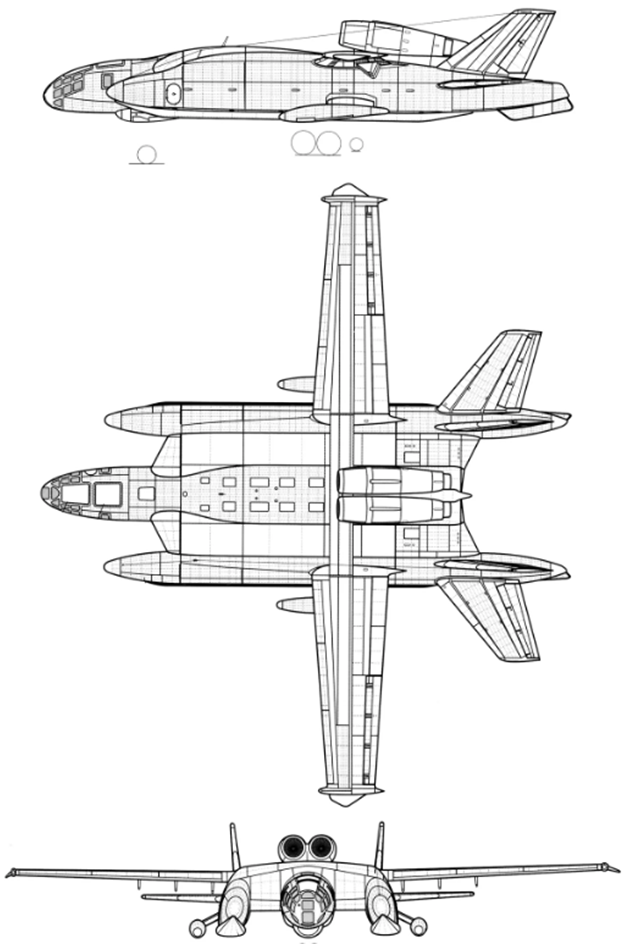
Na prática, o ekranoplane WIG-VVA-14 foi construído de acordo com este Esquema (veja a Fig. 9) e várias versões de maquetes promissoras de ekranoplanes, onde as arruelas da extremidade do skeg desempenham o papel de rejeição vertical frontal (veja a Fig. 10).


a.


b.


c.

Fig. 9 WIG Bartini VVA-14. A. Desenho. b. Modelo em 3-D. c. Foto da amostra atual na água.



Fig. 10. Layout promissor ekranoplan grande.

Tipos de manobras de ekranoplan devido à plumagem vertical:

• Duas quilhas espaçadas idênticas fornecem o modo "Deslocamento lateral" com rotação simultânea em uma direção. Ao mesmo tempo, o Wingplane é deslocado de uma pista para outra sem rotação do casco. Nesse caso, a plumagem horizontal trabalha em direções diferentes, compensando o momento de adorno da plumagem vertical.
• Se as quilhas forem giradas em direções diferentes no mesmo ângulo, surge um momento de rotação, girando o corpo da WIG em torno de um eixo vertical. Nesse caso, a cauda horizontal não funciona, pois o momento da cauda vertical não ocorre.
• Se as quilhas forem giradas em direções diferentes em diferentes ângulos acordados, haverá uma rotação ao longo de um caminho circular (circulação), onde o vetor de velocidade coincide com a direção do eixo longitudinal da fuselagem de Ekranoplan, e o próprio Ekranoplan voa ao longo de um determinado caminho circular com velocidades angulares iguais e rotação do próprio Ekranoplan em torno de eixo vertical.
  
  Nesse caso, a plumagem horizontal trabalha em direções diferentes, compensando o momento de adorno da plumagem vertical.

Todos esses modos praticamente não são praticáveis ​​no modo manual, uma vez que a baixa altitude simplesmente não deixa tempo para uma reação no ritmo da percepção humana. Para controlar o ekranoplan, você precisa de automação de controle, semelhante à estabilização automática de caças ultra-instáveis ​​da geração 4-5.

Conclusão

Todas as premissas acima são baseadas em dados experimentais publicados abertamente (gráficos de pressão do ADT na asa e outros dados).

Uma grande quantidade de dinheiro foi investida em aerodinâmica experimental ao longo do século passado para a construção de ADT de vários tipos e tamanhos, e uma enorme quantidade de material real foi obtida em experimentos com modelos de várias aeronaves e elementos individuais das asas.

É surpreendente que, no processo de ensino, os alunos não confiem nos materiais de experimentos reais, mas em teorias duvidosas de 100 anos atrás. E isso apesar do fato de os próprios dados experimentais contradizerem claramente essas teorias cobertas de musgo.

Mesmo em um curso introdutório generalizado como "Introdução à aerodinâmica" para a FALT FizTech, modelos explicativos qualitativos do conceito básico de "Força de elevação da asa" não são apresentados, mas são substituídos por malabarismos abstratos como fórmulas matemáticas (que, além disso, não permitem calcular nada).

Na ciência, tem havido uma tendência a uma divisão entre teoria e aplicações práticas de engenharia no desenvolvimento de produtos específicos. As contradições óbvias nos modelos teóricos não são anunciadas, mas, pelo contrário, são silenciosas de todas as formas possíveis, para não abalar a autoridade dos idosos musculosos e já falecidos da Academia de Ciências e não interromper a marcha vitoriosa de seus erros sinceros nas páginas de livros e monografias bastante modernos.

PS Após a publicação da primeira parte deste artigo, houve uma discussão sob o artigo de que aproximadamente as mesmas idéias foram ditas em 2003 por um professor de Cambridge que ministrou o curso "Aerodinâmica" lá. Na mensagem, havia um link para um vídeo com uma palestra de um professor sobre esse tópico, bem como um link para um artigo em que, na última página, exatamente o mesmo método de pressão por um fluxo de ar dobrado foi descrito, como descrevi neste artigo.
Fiquei incrivelmente satisfeito por agora não precisar lutar contra todos os ataques, mas você pode apenas se referir ao professor de Cambridge e seu artigo em uma revista científica britânica de 2003.

Aqui está a mensagem com os links:
"
Joehopkins7
24 de fevereiro de 2019 às 22:35
-1
Assistindo a vários vídeos sobre aerodinâmica, deparei-me com uma interessante palestra sobre aerodinâmica do professor Cambridge.
Em 2003, um professor de Cambridge expôs aos alunos da palestra exatamente os mesmos pensamentos que o autor do artigo discutido aqui.
Cheguei a suspeitar que o autor é simplesmente um plágio.
Mas como ele não se referiu aos cientistas ingleses no artigo e não citou esses vídeos para sua defesa, podemos acreditar em sua honesta descoberta independente da descoberta de outra pessoa.))

Aqui está um link para a palestra
www.youtube.com/attribution_link?a=nfUWqs-6T7M&u=%2Fwatch%3Fv%3DH2RRiF24L4A%26feature%3Dshare&fbclid=IwAR2NOfdqNs0HK9WbCp-OYwy0Yqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq

Há também um link para um artigo em que, em 2003, um professor da Universidade de Cambridge na revista científica inglesa escreve exatamente a mesma coisa que o autor de um artigo sobre Habré

www3.eng.cam.ac.uk/outreach/Project-resources/Wind-turbine/howwingswork.pdf
.. "

A força de elevação da asa. Parte 2

Monin Ilya Alekseevich, Ph.D., imoninpgd@gmail.com

Para entender a ordem de desenvolvimento da “aviação” como um ramo da indústria e a “aerodinâmica” como uma ciência, é necessário lembrar que primeiro a primeira aeronave construída por engenheiros entusiasmados em um palpite apareceu (veja a fig. 11), e só então começaram a aparecer os teóricos que criaram disciplina "Aerodinâmica" com base nos resultados da criação de engenheiros de projeto.
Na foto, o avião criado pelo motorista Henri Farman é uma alteração do avião de pequeno porte adquirido da Voisin. Ao mesmo tempo, a aeronave inicial dos irmãos Voisin começou a ser produzida apenas em 1907. No momento da compra de Farman, os aviões da Voisin só podiam saltar um pouco e voar algumas dezenas de metros. Farman, depois de uma série de alterações na aeronave original, conseguiu a oportunidade de voar mais de 1000m, enquanto ainda se virava e fazia um círculo para pousar. O vôo recorde de Farman ocorreu em 13 de janeiro de 1908. E já em 1909, a empresa dos irmãos Farman abriu sua própria produção de aeronaves de seu próprio projeto e uma escola de vôo para ensinar-lhes a arte de voar nelas (ver figura 12). A velocidade de vôo de Farman era então de cerca de 60 km / h, o que foi mostrado em um vôo recorde a uma distância de 180 km, superado em 3 horas de vôo.



Fig. 11. Uma maquete do avião de Voisin convertida para um vôo recorde por Farman em 1907-1908.




Fig. 12. O layout da aeronave "Farman IV-1910". no museu e uma foto de uma amostra genuína no aeroporto.

É claro que as primeiras aeronaves iniciais eram de baixa potência, luz e baixa velocidade.
Esses parâmetros correspondem aos primeiros perfis finos convexos-côncavos, mais semelhantes à folha de compensado curvado mais simples, e não a um perfil complexo com um erro de cálculo teórico profundo.
Para referência, dou uma ilustração da transformação dos perfis das asas desde o início do século XX na indústria da aviação totalmente desenvolvida em meados dos anos 40. (ver fig. 13)



.13. 20- .

. As asas finas não podiam suportar tal escala e peso de maneira que exigisse a instalação de vigas altas e fortes no interior da asa, e a própria asa deveria ser plana-convexa ou mesmo duplamente convexa para ocultar a viga de suporte atrás da bainha aerodinâmica.
20- .
1940- , , . .
30- «», , ().

1939 ( ) -101, .
5–52 /
Re número por 1 ma 3,6 3.6 106

1.7

(α) ±20°
(β) ±180°
:
() 24x14
24
:
: 18
: 30
: 35 2

, , -101 , .
, , , - 20- , . , 1980- (..14).


.14. « ».

, - 1960-80- (.15), 1930- (.16).
30- .
-25, 1933 , . , .
-25 , , . 4000 88., 50/., 500 104/ (29 /) . , ( ), -25 165/ (.246/ ), 10-12. 75-80 .

A.
B.
B.

Fig. 15. WIG "Monstro Cáspio": a.) Em voo. B.) Ainda na água, rosto cheio. c.) Estacionário em projeção frontal.

A.
B.


Fig. 16. Avião gigante ANT-20 "Maxim Gorky", 1939 a) Seção esquemática. B) Fotos no aeroporto e durante o pouso.

Zonas estagnadas durante o fluxo de ar em torno de corpos de formas complexas como ferramenta para formar um perfil virtual das asas.

Muitas vezes existem casos. Quando é necessário construir linhas de fluxo de ar em torno de corpos cuja forma dificilmente pode ser chamada de aerodinâmica.
, , , .
, .
, . « » [3] (.435-437), , « » . « ». , ( ) - .
« ».
(..17), , .
, «» .
(..18), (..20).



.17. , .




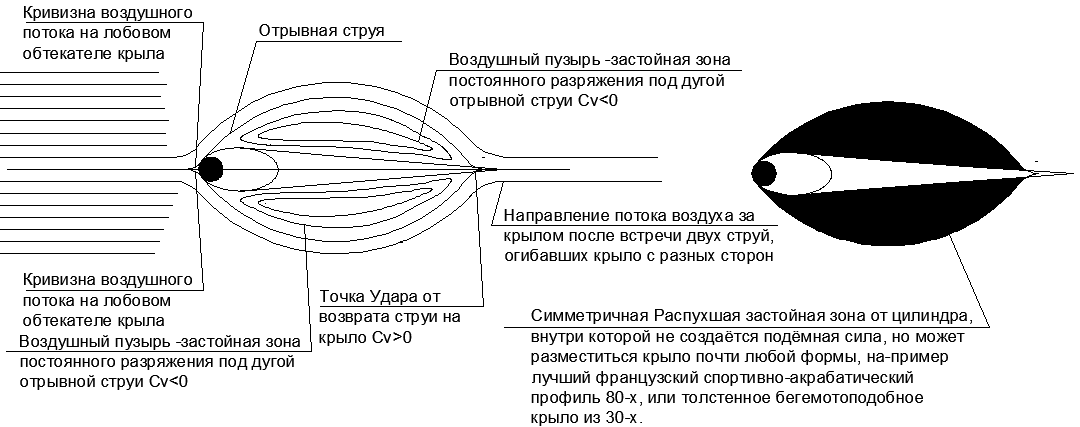.18. « ».

« » , -, .
=0,06, =0,4..0,5, =1.
. , . . , (..19.)
, , , . « » . , .



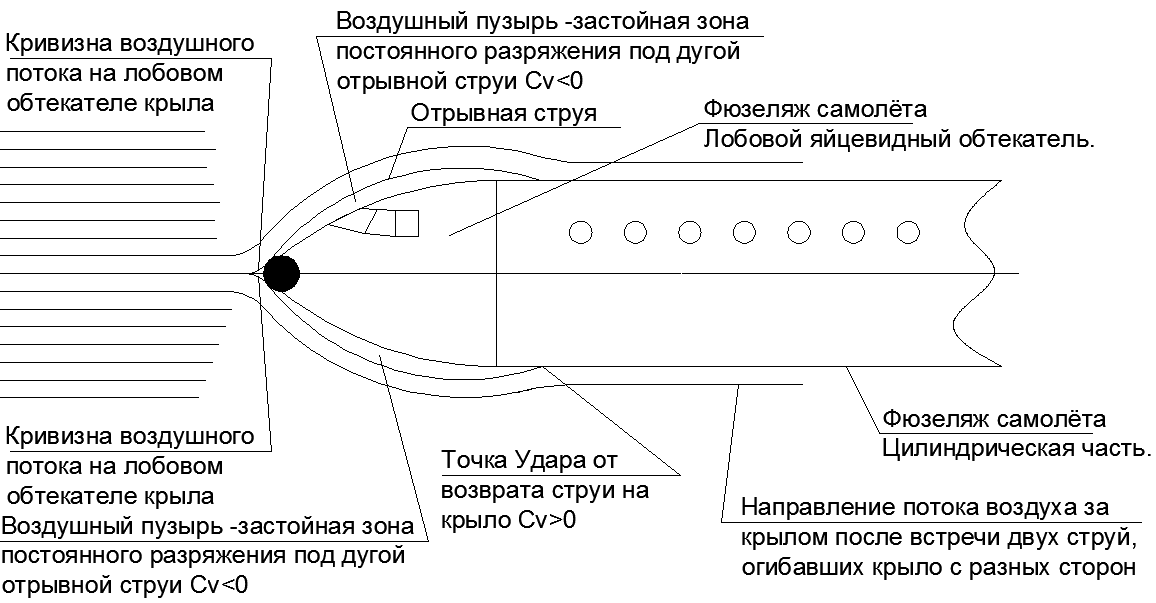
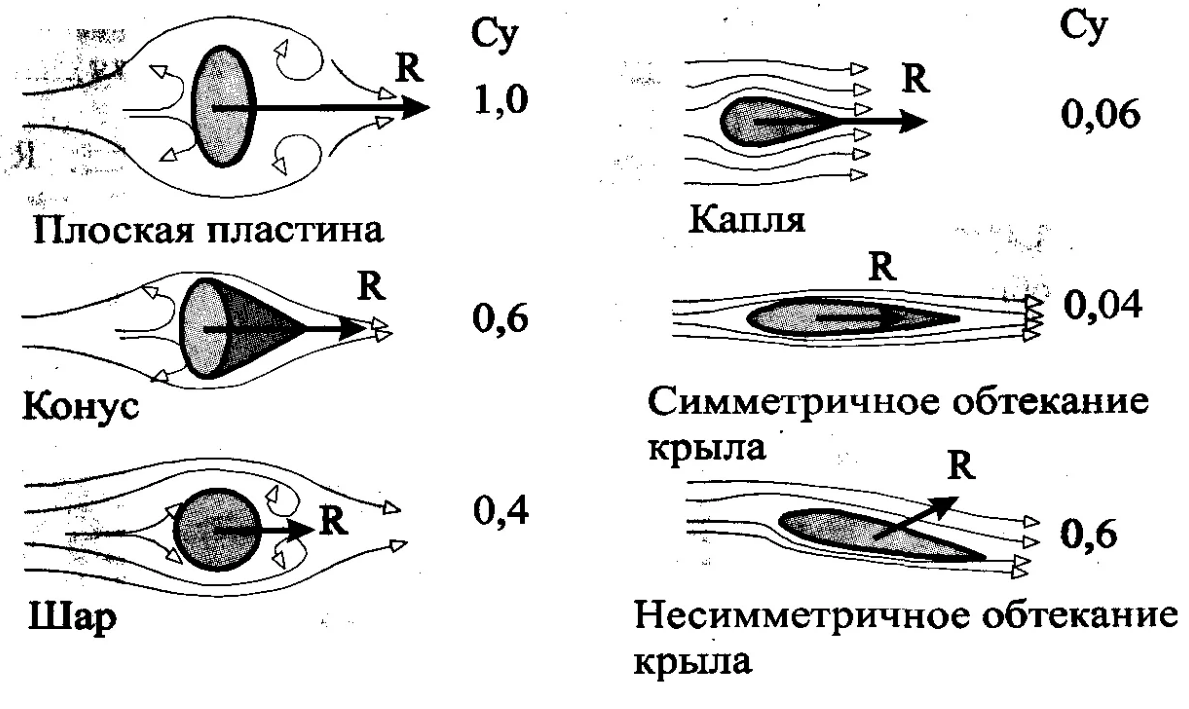
Fig. 19. , . . .

(..20).
. , , .
.
. « »= « » .
« » . , « » . (. .21)



.20. « ».






.21. . ( - ).

«» , , .
, , .
( 15 ), .
. - , « » «- ». , -20 « ».
( ) . « » , (..22).
(..22-2). www.youtube.com/watch?v=Sd4ycAtYcJA . .


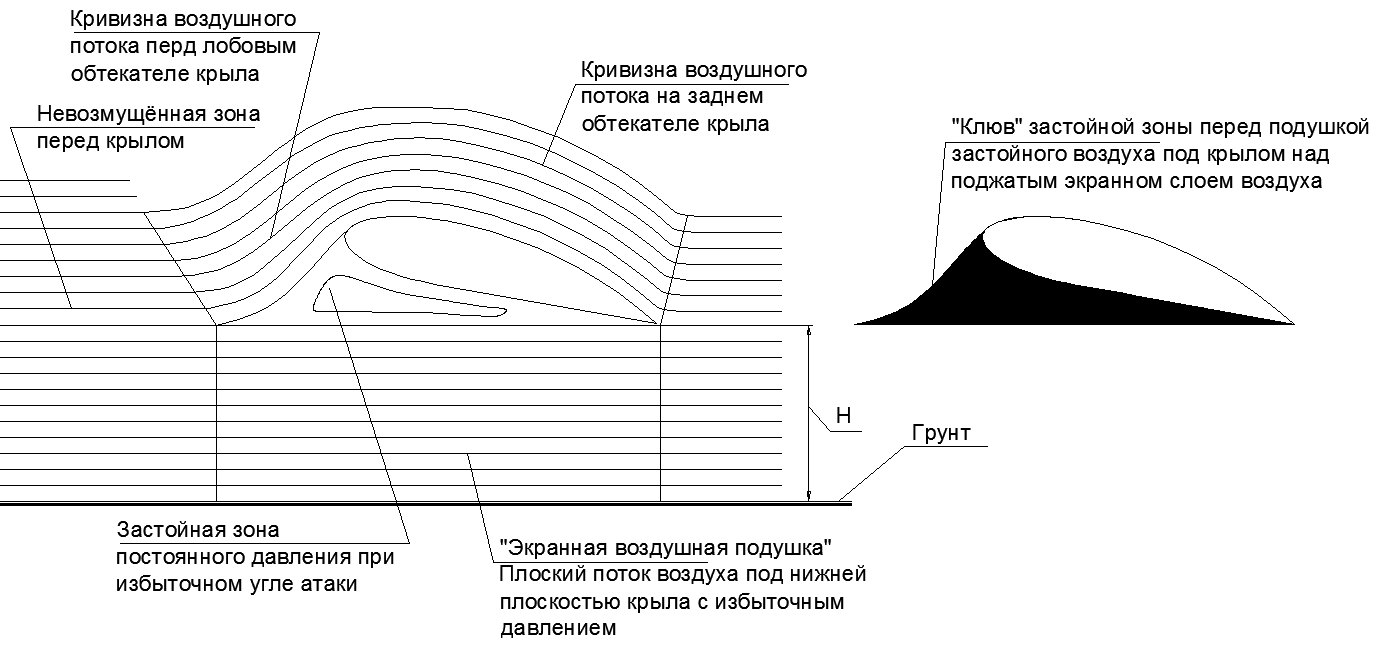.22. « ».


.22-2. , -747 .

-14 (), -20 « ».
1930- , -20 « ». , , (. .16.).
, 198/ ( 220/).
-20 , , « » .
« » 1930- « » 60- (..5)

.5. -20 « » 1934. « » 1966.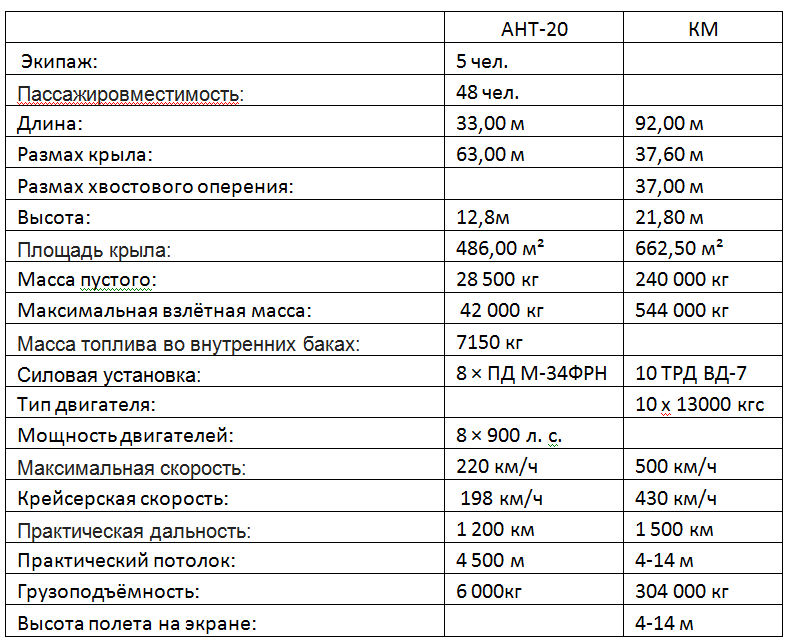


, - .
.
: 544/42= 13
: 662/486=1,36
: 13/1,36=9,5
: 430/198=2,17
: 2,17^2= 4,71
: (10*1300*9,81*430/3,6) /(8*900 000*0,735)=28,8
: 304/(42-28,5)= 22,51.
: 1500/1200=1,25
-20 = 7150/(1200*6)=0,993 /(*)
, .
0.8/(*) -7.
10*13000*0,8=104 000/
, .
2*13 000*0,8=20 800/
1500/430=3,5
1500 104*0.5+3,5*20,8=100 .
200 .
100 000/(1500*200)=0.333 /(.).

Conclusões das relações obtidas:
1. Em termos de economia de combustível, o KM pode ser otimista três vezes mais econômico que o ANT-20.
Agora, o moderno avião de passageiros Airbus A380 possui uma modificação de carga A380F com a capacidade de transportar cargas de até 150 toneladas a uma distância de 10.370 km. A massa máxima de decolagem é de 560 toneladas (a massa da própria aeronave é de 280 toneladas). Calculamos a economia para a versão de carga a partir desses indicadores e fornecemos 130 toneladas de combustível e 150 toneladas de carga a uma distância de 10370 km: 130.000 / (150 * 10370) = 0,0835 l / (t * km).
Em termos de passageiros, o indicador é diferente: “Entre os transatlânticos, o mais econômico é de três litros de combustível por passageiro a cada cem quilômetros (54 milhas náuticas) da rota. Segundo a Airbus [5], por passageiro, o A380 consome 17% menos combustível do que a “maior aeronave moderna” (aparentemente, o Boeing 747 se destina). „

Ou seja, com uma contagem de teste de 850 passageiros com bagagem e assentos, temos um indicador próximo ao cálculo para a versão de carga.
Acontece que não apenas começamos a voar 4-5 vezes mais rápido nos últimos 80 anos, mas também melhoramos a eficiência de combustível mais de 10 vezes do ANT-20 e 4 vezes do Ekranoplan KM. Embora apenas 20 anos atrás, nosso airbus voou 5 vezes mais rápido que o ANT-25. A recente desaceleração nas aeronaves de passageiros é causada pela luta por voos com baixo consumo de combustível.
2. A velocidade de cruzeiro do KM é tão alta à força, pois a uma velocidade mais baixa ele simplesmente não consegue voar na tela. A condição de vôo na tela é o cumprimento da desigualdade "Speed ​​head"> "Average wing load", ou seja,
Pv = 8560Pa a 430 km / h (120m / s)> 544000 * 9,81 / 662,5 = 8055Pa.
3. A segurança de vôo de uma aeronave gigante de baixa velocidade dos anos 30 é muito melhor do que a de uma aeronave alada de alta velocidade dos anos 60, correndo quase incontrolavelmente entre navios de movimento lento e as onipresentes aves aquáticas.
4. O custo da operação de ekranoplanes baseados no mar é muito mais caro do que para aeronaves terrestres de alta altitude. Isso ocorre devido ao número excessivo de motores necessários apenas para iniciar a partir da água e sair para o voo de tela, bem como devido à extrema agressividade da água do mar quando exposto a motores e projetos ekranoplan ao voar nas nuvens devido a salpicos de ondas do mar próximas.
5. Para o Ekranoplan KM, a qualidade da asa ao voar em dois motores é igual à razão entre seu empuxo e o peso do Ekranoplan K = 544 / (13 * 2) = 20,9. Assim, a eficiência aerodinâmica de um Ekranoplan grande e pesado está no nível de eficiência dos melhores grandes aviões modernos com qualidade de planador da ordem de K = 18-20.
6. O mistério para mim é a diferença tríplice em termos de economia do KM Ekranoplan com o Airbus 380F: Por que, com a mesma qualidade da estrutura da aeronave, a Airbus tem 4 vezes melhor economia de combustível?
Ou todo o segredo está oculto na terrível gula dos antigos motores turbo-soviéticos em comparação com os modernos motores turbofan com alto grau de desvio?

A força de elevação da asa. Número da peça 3.

Exatamente um ano se passou após a primeira publicação em Habré do meu artigo (02/02/2019) sobre a explicação da força de elevação da asa sem a equação de Bernoulli.
Um artigo do ano ganhou mais de 41 mil visualizações e ocupou uma posição de liderança nas pesquisas do Yandex pela consulta "wing lift", que aparece no topo da primeira página imediatamente após a definição da Wikipedia.
Também em mensagens privadas recebi muitas informações valiosas e críticas extremamente importantes.
Não editarei as partes escritas anteriormente, mas analisarei algumas declarações erradas duplicadas a partir das mesmas declarações errôneas dos livros didáticos.

Observação 1.
A observação principal acabou sendo que eu citei e interpretei erroneamente as imagens de comparações visuais dos arrastões aerodinâmicos de vários corpos de rotação para vôo.
Por isso, considerei essa resistência a resistência correspondente de Cx para aeronaves polares, e a imagem de algum livro (Fig. 19 na segunda parte) geralmente mostra a designação errada Su em vez de Cx.
Eles me explicaram que, de fato, para corpos individuais de revolução, o coeficiente Cd será elegível, o que liga a seção transversal (meia nau) do objeto que está sendo soprado com a pressão de velocidade exercida por ele.
O valor de Cd nos melhores carros de corrida não cai abaixo de 0,27.
Além disso, para corpos em forma de eixo-árvore e um perfil de asa sem força de elevação, o coeficiente de arrasto é declarado em 0,06 a 0,04, o que nunca é possível para o índice Dx.
Um Su tão baixo, como 0,06 ... 0,04, não é um engano direto, mas é enganoso devido à ocultação de circunstâncias e às nuances do cálculo. Portanto, o valor de Cd é calculado a partir da razão para a seção transversal (seção mestra), e o valor de Cx é calculado a partir da razão para a maior área da asa na projeção vertical, ou seja, para a maior área da asa na direção longitudinal à força de arrasto efetiva.
Assim, em imagens coloridas que demonstram a racionalização de vários corpos em voo, eles começam a comparar incorretamente o “Longo” com o “vermelho”, ou seja, comparar os valores em dimensões incomparáveis.
Os valores reais do arrasto Cd, referentes à seção “meio”, consulte a tabela abaixo.

Tab. Os valores das arrastagens aerodinâmicas frontais de corpos Cd de várias formas.
A mesa da esquerda é o corpo da revolução. A tabela à direita é a viga de uma determinada seção.


Observação 2.
Habr é um excelente recurso para publicar artigos científicos e técnicos de vários perfis, mas suas regras conferem poderes surpreendentemente amplos aos "trolls negativos" que, com seus desgostos, levam o karma do autor a um profundo sinal negativo, privando-o da capacidade de responder a comentários críticos e fazer novas publicações seus artigos. Existem até artigos publicados em Habré sobre esse recurso do Karma on Habré.
Como resultado da queda do meu Karma abaixo de -30, fui impedido de comentar meus próprios artigos, além de ser privado do direito de publicar.
A exceção é este artigo sobre aerodinâmica, onde milagrosamente me foi deixado o direito de editar.
Usarei esse "buraco de oportunidade" para publicar uma nova parte do artigo, ignorando o carma negativo.
Você pode enviar todos os seus comentários e desejos para mim em “mensagens pessoais” no próprio Habré ou no meu endereço de e-mail imoninpgd@gmail.com, que também é indicado no início de cada um dos meus artigos.
Fico sempre feliz em responder a mensagens privadas com críticas construtivas de maneira educada.

A aplicação prática de asas de raio curvo fino em projetos modernos.

Como se viu, as finas asas de raio côncavo côncavo consideradas na primeira parte agora são usadas ativamente como lâminas rotativas em grandes túneis de vento (ver fig. 23, 24)
A figura mostra claramente que essas lâminas finas são usadas com precisão para girar o fluxo, como no meu artigo.
Não há dúvida de que os projetistas dessas lâminas rotativas estão cientes das tensões mecânicas experimentadas por essas lâminas pelo fluxo nelas.
Também é indubitavelmente fácil medir a pressão nas pás de um fluxo de ar curvo nas partes convexa e côncava dessas pás. Além disso, a medição da pressão pode ser realizada para uma corrente de espessura e para uma lâmina de lados diferentes.
Acredito que não será difícil para as pessoas com acesso ao TsAGI ADT aliviar a pressão das lâminas do apêndice guia do ADT pelas células de carga durante uma das experiências atuais.



Fig. 23. O perfil da lâmina aerodinâmica usada em um túnel de vento moderno como dispositivo de endireitamento rotativo de ajuste de tipo no duto de ar do ADT.




Fig. 24: Localização das lâminas rotativas no trato ADT na visualização 3D.


A foto (Fig. 25) mostra os perfis das pás do rotor de uma turbina a gás de um determinado livro didático sobre "Hidrodinâmica do gás", que discute os elementos estruturais das turbinas a vapor e a gás de energia.
Essas lâminas repetem quase exatamente o perfil da asa convexa-côncava fina e curva descrita na 1ª parte teórica deste artigo, assim como os métodos para calcular as cargas nas lâminas a partir do fluxo de gás nesses livros didáticos de hidroginástica coincidem com o procedimento descrito na 1ª parte este artigo.
Uma característica distintiva da operação das pás do rotor da turbina é que, quando o gás se curva em torno da superfície das pás, o próprio gás não altera a densidade e a temperatura, mas apenas altera suavemente a direção do vetor de velocidade do fluxo de gás, sem alterar o módulo de velocidade do gás se considerarmos o fluxo de gás em coordenadas com referência a a própria lâmina da turbina. Ou seja, as condições operacionais de uma lâmina de rotor de turbina individual praticamente reproduzem exatamente as condições operacionais de uma única asa fina e curva no espaço livre.

É surpreendente que o que afirmei no artigo seja conhecido e amplamente utilizado nos cálculos aplicados em hidroginomecânica ao projetar turbinas a gás para engenharia de energia e motores de aeronaves, enquanto os adeptos da aerodinâmica não percebem esses modelos teóricos e teóricos de " Hidro-gasodinâmica ”, considerando“ Aerodinâmica ”e“ Hidro-gasodinâmica ”como ciências diferentes com leis de interação diferentes para asas sólidas completamente idênticas com o mesmo ambiente de gases e líquidos ao seu redor.



Fig. 25. Perfis das pás de trabalho de uma turbina a gás e visualização do fluxo de gás nelas.

Flutter

Durante o rápido desenvolvimento da aviação na década de 1930, na busca de altas velocidades, um fenômeno surpreendente chamado Flutter apareceu inesperadamente, quando a uma certa velocidade da aeronave subitamente aumentaram de repente as vibrações torcionais das asas, levando à destruição da aeronave em poucos segundos.
Lidamos com esse problema por métodos construtivos, aumentando a rigidez à torção e à flexão das estruturas das asas, mas as explicações teóricas permaneceram no nível de "Soluções Empíricas Intuitivas", embora o acadêmico Keldysh tenha recebido o Prêmio Stalin por essas soluções.
Nos livros didáticos de aerodinâmica (consulte a bibliografia), não encontrei capítulos explicando a vibração.
Assim, darei explicações para o fenômeno Flutter não com base em nenhuma teoria oficial, mas simplesmente derivando as consequências das disposições teóricas descritas na primeira parte do artigo.
Conforme descrito na primeira parte, um fluxo com um raio de curvatura de pelo menos
R = 2 * Rbt.
Onde Robt é o raio do arredondamento do dossel da carenagem da asa.
Nesse caso, a espessura do fluxo desviado em cada direção da asa é Hp = Robt.
Da construção geométrica, segue-se que o ângulo do vetor de velocidade do fluxo separado ao tocar sua carenagem na direção do vôo é A = 48 graus.
A projeção vertical da velocidade do fluxo separado é Vp. vert = Vp * sin A = 0,743 * Vp.
Ou seja, obtivemos uma estimativa superior da velocidade vertical para o fluxo de separação, uma vez que os critérios para a estimativa limitante do raio do fluxo curvo R = 2 * com a espessura do fluxo desviado para um lado do fluxo = já foram obtidos em nossa ferida.
Com mais movimento acima do perfil curvo da asa, um fluxo separado com a energia inicial
Ep.vert. = Vvert.n ^ 2 * q * Robt
deve extinguí-lo devido ao trabalho da diferença entre a pressão do ar ambiente e a pressão na superfície da asa sob um fluxo separado, ou seja, devido ao trabalho da pressão de descarga acima do plano da asa.
Drive = Notre * Drive
Ou seja, a igualdade E.vert = Evozd deve ser cumprida
Vvert.n ^ 2 * q * = Notre * Rzd
A altura do envelope da bolha sem interromper o fluxo do perfil:
Notre = Vp. ^ 2 * q * Robt / Rvozd
Substituindo a expressão por V. vert = V * sin À obtemos:

Notre = (Vp * sen A) ^ 2 * q * Robt / Rzvod = Vp. ^ 2 * q * sen A ^ 2 * Rbt / Rzd
Ou seja, em uma altura de perfil acima desse valor, o fluxo flui sem a formação de uma bolha de separação.
Se o valor da corcunda do perfil atrás da carenagem frontal for menor que o valor de Notre, o fluxo fluirá pelo perfil com a formação de uma bolha de ar com descarga e ar estagnado no interior, detectados visualmente pelas vibrações da seda.
Em seguida, surge a questão do comprimento da bexiga estagnada sob o fluxo separado.
Se assumirmos que a queda de pressão do ar é constante, a frenagem do fluxo de ar será acelerada uniformemente, e a curva do limite da bolha de separação parecerá uma parábola com a corcova para cima.
O tempo de desaceleração completa do fluxo verticalmente é T = V vert / A.vert
Onde A.vert = Rvozd / (Robt * q)
Temos Tpuz1 = V vert / A.vert = V vert * (Robt * q) / Rvozd
O comprimento da bolha destacável L1 até o topo será
Lpuz1 = Vp * Tpuz1 = Vp * V vert * (Robt * q) / Rvozd = Vp * (Vp * sin A) * Robt * q / Rzvoz =>
Lnav1 = Vn ^ 2 * q * sen A * Robt / Rvozd
A partir da fórmula obtida Luz1 para o comprimento da parte ascendente do fluxo separado acima da bolha separada (ou perfil ideal), podemos concluir que, para alguns valores da velocidade de vôo V e da espessura da carenagem frontal Robt, pode ocorrer uma situação em que o valor da bolha separada L bel 1 + 2 = 2 * Lpuz1 pode exceder a largura da asa Vkr.
Quando a expansão da bolha de arranque atinge a borda traseira da asa, e o fluxo decrescente sai atrás da borda da asa, o ar de alta pressão entra sob a bolha de arranque da pista emaranhada.
Após a equalização da pressão na bolha de separação com a atmosfera, a diferença de pressão entre a atmosfera e a bolha acima da asa deixa de atuar no fluxo de separação. Depois disso, o fluxo destacável se desprende da carenagem e não pode mais voltar para a asa, criando assim uma paralisação completa do fluxo.
Com um vôo horizontal de alta velocidade acima da velocidade normal calculada para uma aeronave em particular, com tal estol de fluxo acima do plano superior da asa, outros eventos se desenvolvem na seguinte ordem (consulte a fig. 26):
- Fluxos separados formam bolhas destacáveis ​​de tamanhos diferentes na asa com um pequeno ângulo de ataque, enquanto a força total de elevação resultante da asa é F1 = F. Up-Fk. Abaixo, e o torque relativo ao ponto central tem um valor calculado na alavanca L1
- Ao acelerar para Vf, o fluxo separado acima do plano superior da asa atinge a borda traseira, e o Fk2 resultante se torna maior que o Fk1 calculado. Além disso, o torque da asa do aumento do braço L2 aumenta significativamente, aumentando o momento do mergulho.
- Quando o fluxo é interrompido, a força de elevação do vácuo na bolha de separação superior desaparece.
- No caso de um desaparecimento acentuado do vácuo acima da superfície superior da asa, a descarga instantânea das estruturas da asa ocorre apenas de um lado.
- No plano inferior da asa, o estol de fluxo ainda não ocorre e, portanto, uma força aerodinâmica significativa continua para baixo a partir da bolha de separação desenvolvida, que é muitas vezes maior que a força de elevação normal da asa.
Assim, há uma forte sobrecarga da asa para dobrar para o outro lado, ou seja, para baixo, com a asa torcendo para a curva.
Como resultado, o avião cai acentuadamente, levantando o nariz e perdendo velocidade.
Quando a asa é torcida com a borda traseira para baixo, o ângulo de ataque de toda a asa aumenta acentuadamente, como resultado do aumento da frenagem no fluxo de ar, enquanto a bolha de separação entra em colapso e a força de elevação na superfície inferior da asa muda seu sinal bruscamente, dobrando a asa novamente para cima.
Quando a direção normal de sustentação é restaurada, a asa começa a dobrar bruscamente para cima, e o momento das forças normais de sustentação recém-criadas torce a asa e gira a asa com toda a aeronave para fora do cabo de mergulho.
Assim, o ciclo fechou e passou para o segundo turno.
A aeronave entra em aceleração, o fluxo é restaurado sem parar ao longo do plano superior da asa e, depois que uma nova velocidade crítica é atingida, a parada ocorre novamente e as sobrecargas de flexão da asa com torção são repetidas.
Tal agitação de fluxo rápido com curvas alternadas e torção das asas (com cargas várias vezes maiores que a estática calculada) inevitavelmente leva à rápida destruição das asas.



Fig. 26. Fases de desenvolvimento da vibração das asas:
1) Força de elevação normal F1 antes do início do flater, onde a área do retângulo sombreado mostra as forças de pressão resultantes na asa dos fluxos simétricos separados.
2) Elevação excessiva na asa Fk2 com velocidade crescente acima da calculada. A partir da força excessiva de elevação F2 da força no ombro muito aumentado L2, um forte torque de mergulho é gerado logo antes do fluxo interromper o plano superior e o início da vibração.
3) Pare o fluxo do plano superior da asa com vibração desenvolvida. No plano superior, o elevador desaparece devido à equalização da pressão com a atmosfera. A força não compensada da bolha de corte inferior cria uma sobrecarga da asa com uma enorme força Fc3 em direção ao solo, e o torque na asa muda drasticamente para o cabeamento.
4) Com um aumento acentuado no ângulo de ataque da asa, o fluxo de ar que entra extingue a bolha de separação com pressão reduzida no plano inferior da asa, como resultado da força de elevação muda de direção para normal, ou seja, para cima, com a restauração do torque no mergulho calculado.

É uma oscilação de asa de flexão torcional de repetição rápida e cíclica a uma certa velocidade crítica Vf que eles chamam de Flutter.
A destruição da asa de Flater pode ser evitada por um forte reforço das estruturas da asa. Esta é a recomendação no "nível intuitivamente empírico" que Keldysh fez.
, , , .
«» «». «» «», .
, . .
, .
R, V .
, .
, , .
, ( ) .
, , « » .
, .
- , , .
.


R , .
1930- 300-400/, .
R , -3 1940.
, .
!
— «» «». , .
, .
-16 -3 ( ). 75-170 / ( 420/ 470/), , -3 ( 495/, 640/).
-3 -16 495/420=1,18.
, 20% 1,44 .
20% 1,5 , (, , ), .
-3, -16, .
2,5-3 , .
800-900/, V, . , , .
- .
… 1939 ( ) -101. , -101 , ( 52/ 187/) 1930-, . , .
(..27).
.
— — , . , . , -1 .
, , . (..28)


.27. . , . .




.28. ( — ). — . - 100%.

:

• « », .., , , 1986.-413.
• «» 1, .., , , 2018,-496.
• «», . .., , ...,2017,-607.