Tendo nos encontrado em 2019 e descansando um pouco do desenvolvimento de novos recursos para o Smart IDReader, lembramos que não escrevíamos nada sobre processadores domésticos há muito tempo. Portanto, decidimos corrigir com urgência e mostrar outro sistema de reconhecimento na Elbrus.
Como sistema de reconhecimento, o sistema de reconhecimento de objetos de pintura foi considerado "sob condições não controladas pelo método com treinamento de acordo com um exemplo" [1]. Este sistema constrói uma descrição da imagem com base em pontos singulares e seus descritores, que busca em um banco de dados indexado de imagens. Analisamos o desempenho desse sistema e identificamos a parte de baixo nível mais demorada do algoritmo, que foi otimizada usando as ferramentas da plataforma Elbrus.
De que tipo de sistema de reconhecimento estamos falando?
Atualmente, a maioria dos museus e galerias usa várias ferramentas para se familiarizar independentemente com a exposição. Juntamente com os guias de áudio clássicos, os aplicativos móveis que usam métodos de processamento e análise de imagem se espalharam. Algumas dessas aplicações reconhecem códigos de exibição gráfica (bar ou QR) [2], para outras [3-4] os dados de entrada são molduras de foto ou vídeo com uma exibição tirada em close (Smartify, Artbit). Obviamente, os “guias móveis” desta última categoria são mais convenientes para o usuário [5] do que as soluções com entrada manual do número da exposição ou reconhecimento QR: o número e o código são bem pequenos, e sua pesquisa e entrada exigem ações adicionais que não estão relacionadas à revisão da exposição. É um sistema que consideraremos.
A tarefa de reconhecer pinturas em imagens foi formulada da seguinte maneira. Solicitar Imagem Q deve ser atribuído a uma das classes C = \ {C_i \} _ {i \ em [0, N]}C = \ {C_i \} _ {i \ em [0, N]} onde C i - classe de imagem eu expor em i e m [ 1 , N ] , C 0 - uma classe de outras imagens correspondentes ao valor "imagem desconhecida". Para cada C i conjunto de imagens de referência T i .
Além disso, fomos guiados pelas seguintes premissas:
- Solicitar Imagem Q obtido usando a câmera de um dispositivo móvel por um usuário despreparado durante o passeio, portanto:
a) pode conter defeitos visuais - brilho, áreas desfocadas, ruído;
b) o ângulo, o enquadramento, a iluminação e o equilíbrio de cores são desconhecidos (Fig. 1a);
c) objetos estranhos, como paisagens, molduras, visitantes, podem estar presentes na imagem (Fig. 1b). - Imagem de referência T É uma imagem de alta resolução com uma projeção frontal de uma imagem ou sua reprodução digital. O padrão não contém objetos estranhos e defeitos visuais. Os padrões podem ser, por exemplo, páginas qualitativamente digitalizadas de álbuns de arte (Fig. 2).
- A imagem (a pedido e no padrão) pode ser aplicada a qualquer estilo - realismo,
impressionismo, abstração, gráficos de fractal, etc. - Número de aulas N corresponde ao tamanho da coleção e, para uma galeria, pode atingir
centenas de milhares de exposições [6].

Figura 1 - Exemplos de solicitações de imagem a) uma foto é fotografada de longe com pouca luz; b) um visitante está na moldura.

Figura 2 - Exemplos de imagens de referência para pinturas a) Claude Monet "De Voorzaan en Westerhem", b) Salvador Dali "A persistência da memória"
A idéia principal de nossa solução para esse problema é baseada na construção de uma descrição especial da imagem a partir da imagem de entrada, que é usada para procurar essa imagem no banco de dados de descrições de imagens de referência de imagens de alta resolução que não estão sujeitas a distorções geométricas e outros defeitos de foto. As coordenadas dos pontos singulares encontrados usando o algoritmo YACIPE [7] e seus descritores de RFD atuam como essa descrição.
Para cada referência T i construir uma descrição e depois indexá-la - para cada ponto da descrição, inserimos um registro do formulário l a n g l e i , f i r a n g l e em uma árvore de pesquisa em cluster hierárquica aleatória [8], que permite realizar uma pesquisa aproximada pelos vizinhos mais próximos com um ganho de velocidade significativo em comparação com uma pesquisa linear. A distância de Hamming é usada como métrica, pois usamos um descritor binário.
O processo de reconhecimento é o seguinte:
Na imagem da solicitação Q área de pintura Q L pré-localizado usando a suposição da retangularidade do quadro. A busca de zona é realizada usando o algoritmo de busca rápida em quadrângulos [9], com a restrição da proporção removida. Isso evita os seguintes problemas:
- descrição insuficiente da área da imagem devido a objetos estranhos no quadro, que podem ter pontos especiais com as melhores classificações;
- custos computacionais para comparar descritores de áreas localizadas fora da figura;
- incompatibilidade significativa da escala e do ângulo entre o padrão no banco de dados e a imagem da imagem, o que leva a um resultado incorreto dos descritores correspondentes.
A imagem na zona encontrada é projetada normalizada:
Q ∗ = H ( Q L ) ,
onde H - transformação projetiva.
Crie uma descrição compacta w ∗ :
a) a imagem é reduzida para um tamanho padrão, mantendo proporções, a fim de tornar o algoritmo mais resiliente à escala;
b) o ruído de alta frequência é suprimido por um filtro gaussiano;
c) pontos singulares são calculados na imagem resultante, seu número é artificialmente limitado a M O melhor por avaliação interna do YACIPE;
d) são calculados descritores em cores de RFD das vizinhanças dos pontos singulares encontrados, pois em nossa tarefa era importante salvar informações sobre as características de cores das imagens de entrada. Por exemplo, as figuras na Fig. 3 seria extremamente difícil distinguir sem ele;
d) assim, a descrição da imagem Eu pode ser representado como: w ^ * = \ {\ langle p_i, f_i) \ rangle \} _ {i \ em [1, M]}w ^ * = \ {\ langle p_i, f_i) \ rangle \} _ {i \ em [1, M]} onde pi= langlexi,yi rangle As coordenadas do i-ésimo ponto singular e fi É o identificador para a vizinhança do i-ésimo ponto singular.
Para cada entrada langlep,f rangle emw∗ o índice realiza uma pesquisa aproximada pelos vizinhos mais próximos do descritor f . O procedimento de votação é aplicado aos descritores encontrados - o descritor fi adiciona uma voz ao padrão Ti . Em seguida, são selecionados K candidatos candidatos com o maior número de votos.
Para cada um K as opções selecionadas usando o algoritmo RANSAC, é realizada uma busca pela transformação projetiva H traduzindo, dentro de um determinado erro geométrico delta pontos de consulta Q∗ para pontos de referência T . Par de pontos langlep,p′ rangle com descritores próximos é considerado uma correspondência válida se:
l e f t | H ( p ) - p ′ r i g h t | < d e l t a , p e m w ∗ , p ′ e m w T
Como resultado final, o padrão é selecionado T b para o qual o número de comparações corretas acabou sendo o máximo. Se for menor que um determinado valor limite R , o resultado será a resposta "imagem desconhecida" para evitar falsos positivos (por exemplo, nas imagens para as quais não há descrição do padrão no banco de dados de pesquisa).


Figura 3 - Claude Monet. Catedral de Rouen, Fachada Oeste, Luz do Sol (esquerda) e Catedral de Rouen, Portal e Torre Saint-Romain ao Sol (direita).
Uma das partes principais do sistema é a busca por descritores próximos, usando a distância de Hamming como métrica. Como é calculado várias vezes, esse estágio se torna bastante trabalhoso em termos de computação e leva 65% do tempo do sistema. Por isso, otimizamos.
Uma descrição muito pequena da arquitetura de Elbrus
A arquitetura do processador da Elbrus usa o princípio de uma ampla palavra de comando (Very Long Instruction Word, VLIW). Isso significa que o processador executa instruções em grupos e, dentro de cada grupo, não há dependências e essas instruções são executadas em paralelo. Cada um desses grupos é chamado de palavra de comando ampla. Palavras de comando amplas são geradas por um compilador otimizador, que possibilita uma análise mais detalhada do código fonte, levando a uma paralelização mais eficiente [10].
Um recurso da arquitetura Elbrus são os métodos de trabalhar com memória. Além de ter um cache que otimiza o tempo de acesso à memória, os processadores Elbrus oferecem suporte a um método de hardware / software para pré-paginação de dados. Este método permite prever acessos à memória e bombear dados para o buffer de dados preliminar. O hardware do processador inclui um dispositivo especial para acessar matrizes (Array Access Unit, AAU), mas a necessidade de troca é determinada pelo compilador, que gera instruções especiais para a AAU. Usar um dispositivo de troca é mais eficiente do que colocar elementos do array no cache, pois os elementos do array são frequentemente processados sequencialmente e raramente usados mais de uma vez [11]. No entanto, deve-se notar que o uso do buffer de pré-paginação no Elbrus é possível apenas ao trabalhar com dados alinhados. Devido a isso, a leitura / gravação de dados alinhados ocorre muito mais rapidamente que as operações correspondentes para dados não alinhados.
Além disso, os processadores Elbrus suportam vários tipos de paralelismo, além do paralelismo no nível de comando: paralelismo SIMD, paralelismo de fluxos de controle, paralelismo de tarefas em um complexo de várias máquinas. De particular interesse para nós é a simultaneidade do SIMD.
Recursos do uso do processador de expansão SIMD Elbrus
O uso de extensões SIMD pode ser realizado de dois modos: automático e direto. No primeiro caso, a paralelização de operações é realizada completamente pelo compilador sem a participação do desenvolvedor. Esse modo é limitado, pois o código otimizado deve repetir completamente o comportamento do código-fonte, incluindo o comportamento ao transbordar, arredondar etc. Nesse caso, o comportamento das instruções de extensão SIMD pode diferir nesses aspectos das instruções do processador. Além disso, os algoritmos usados nos compiladores são imperfeitos e nem sempre são capazes de executar uma paralelização eficiente. No entanto, os desenvolvedores também podem acessar os comandos de extensão SIMD diretamente usando intrínsecas. Intrínsecas são funções cujas chamadas são substituídas pelo compilador com código de alto desempenho para uma determinada plataforma, em particular com comandos de extensão SIMD. Os processadores Elbrus-4C e Elbrus-8C suportam um conjunto de intrínsecas, para as quais o tamanho do registro é de 64 bits. Inclui operações para conversão de dados, inicialização de elementos vetoriais, operações aritméticas, operações lógicas bit a bit, permutação de elementos vetoriais, etc.
Ao usar intrínsecos na plataforma Elbrus, atenção especial deve ser dada ao acesso à memória, pois tarefas práticas, por exemplo, tarefas de processamento de imagens, geralmente exigem leitura desequilibrada dos dados em um registro de 64 bits. Essa leitura por si só é ineficiente, pois requer um par de comandos de leitura e um comando subsequente para formar um bloco de dados, mas, mais importante, um buffer de troca de matriz não pode ser usado para aumentar a velocidade de acesso aos dados. No entanto, vale ressaltar que o problema do acesso ineficiente a dados desalinhados é relevante para os processadores Elbrus-4C e Elbrus-8C, enquanto para o Elbrus-8CV mais recente com a 5ª versão do sistema de comando, ele está parcialmente resolvido. Espera-se que os processadores Elbrus com a 6ª versão do sistema de instruções sejam completamente resolvidos.
No entanto, nos processadores Elbrus-4C e Elbrus-8C, o processamento de dados de baixo nível é realizado com eficiência, levando em consideração o alinhamento. Por exemplo, para matrizes numéricas, ela pode consistir em vários estágios: processamento da parte inicial (até a borda do alinhamento de 64 bits de uma das matrizes), processamento da parte principal usando acesso alinhado à memória e processamento dos elementos restantes da matriz. Como a análise de ponteiros durante a compilação não é uma tarefa trivial, você pode usar o –faligned compilador –faligned , com o qual todas as operações de acesso à memória são executadas de maneira alinhada.
O próximo recurso do uso de intrínsecos na plataforma Elbrus está diretamente relacionado à sua arquitetura VLIW. Devido à presença de vários dispositivos lógicos aritméticos (ALU), que funcionam em paralelo e são carregados ao formar palavras de comando amplas, vários comandos podem ser executados simultaneamente. No total, os processadores Elbrus-4C e Elbrus-8C têm seis ALUs que podem ser usadas como parte de uma equipe ampla, mas cada ALU suporta seu próprio conjunto de intrínsecas. Operações simples, como adicionar ou multiplicar elementos em registros de 64 bits, geralmente suportam duas ALUs. Isso significa que o processador Elbrus pode executar duas dessas instruções em um único ciclo de clock. Para fazer isso, o loop de execução deve ser usado no código executável. O compilador de otimização para a plataforma Elbrus suporta o pragma #pragma unroll(n) , que permite a implantação de n iterações de loop.
Um exemplo da implementação da função de adição, levando em consideração esses recursos, pode ser encontrado em nosso artigo anterior.
Os experimentos
Hooray, o texto acabou e finalmente lançaremos algo no Elbrus!
Primeiro, consideramos separadamente a distância de Hamming. Sem mais delongas, comparamos vetores de dois bits de dados aleatórios. Os valores binários foram agrupados em matrizes de números inteiros de 8 bits e, por simplicidade, pensamos que os comprimentos dos vetores originais são múltiplos de 8. Como sempre, o código é escrito em C ++, compilado pelo lcc 1.21.24 - um compilador Elbrus otimizador.
Escrevemos várias implementações da distância de Hamming, que levaram em consideração seqüencialmente os recursos dos processadores Elbrus. Eles ficaram assim:
- Um XOR bit a bit entre números inteiros de 8 bits e uma tabela de valores pré-calculados são usados. Esta é uma implementação básica, sem intrisics e outros truques.
- Ele usa o XOR entre números inteiros de 32 bits e intrínsecos para calcular o número de unidades em um número inteiro de 32 bits - popcnt32. O alinhamento de limite de 32 bits não foi realizado.
- Ele usa o XOR entre números inteiros de 64 bits e intrínsecos para calcular o número de unidades em um número inteiro de 64 bits - popcnt64. O alinhamento de borda de 64 bits não foi realizado.
- Ele usa o XOR entre números inteiros de 64 bits e intrínsecos para calcular o número de unidades em um número inteiro de 64 bits - popcnt64. O acesso à memória é realizado de maneira alinhada. Como os endereços iniciais das matrizes podem ter alinhamento diferente, ao ler uma das matrizes, dois blocos vizinhos de 64 bits são lidos e o bloco necessário de 64 bits é formado a partir deles.
- Ele usa o XOR entre números inteiros de 64 bits e intrínsecos para calcular o número de unidades em um número inteiro de 64 bits - popcnt64. O acesso à memória é realizado de maneira alinhada. Como os endereços iniciais das matrizes podem ter alinhamento diferente, ao ler uma das matrizes, dois blocos vizinhos de 64 bits são lidos e o bloco necessário de 64 bits é formado a partir deles. Além disso, o
-faligned compilador -faligned é -faligned . - Ele usa o XOR entre números inteiros de 64 bits e intrínsecos para calcular o número de unidades em um número inteiro de 64 bits - popcnt64. O acesso à memória é realizado de maneira alinhada. Como os endereços iniciais das matrizes podem ter alinhamento diferente, ao ler uma das matrizes, dois blocos vizinhos de 64 bits são lidos e o bloco necessário de 64 bits é formado a partir deles. Além disso, o
-faligned compilador -faligned e os pragmas do compilador #pragma unroll(2) (para usar as ALUs disponíveis para calcular popcnt64) e #pragma loop count(1000) (para habilitar otimizações de #pragma loop count(1000) adicionais) foram usados.
Os resultados das medições de tempo são mostrados na tabela 1.
Tabela 1. Tempo para calcular a distância de Hamming entre duas matrizes de números binários compactados de comprimento 10 ^ 5 em uma máquina com um processador Elbrus-4C. Tempo médio de 10 ^ 5 começa.
| Não. | Um experimento | Tempo, ms |
|---|
| 1 | tabela de valores calculados | 141,18 |
| 2 | popcnt32, sem alinhamento | 125,54 |
| 3 | popcnt64, sem alinhamento | 58,00 |
| 4 | alinhamento popcnt64 | 17,36 |
| 5 | alinhamento -faligned , -faligned | 17.15 |
| 6 | popcnt64, alignment, -faligned, pragma unroll | 12,23 |
Pode-se observar que todas as otimizações consideradas levaram a uma diminuição de 11,5 vezes no tempo de execução. Vale ressaltar que o uso de intrínsecos para acesso desequilibrado à memória mostrou aceleração apenas 1,13 vezes (para popcnt32) e 2,4 vezes (para popcnt64), enquanto a contabilização do alinhamento de dados levou ao uso do buffer de troca de matriz APB com a ajuda da qual foi possível alcançar a aceleração em outras 3,4 vezes (58 ms versus 17,15 ms). Apesar do uso do sinalizador -faligned não mostrar um ganho de desempenho significativo no exemplo acima, em algoritmos mais complexos, pode haver uma situação em que o compilador não pode analisar o código-fonte suficientemente profundo para gerar comandos para o APB. Levando em consideração o número real de ALUs especializadas, permitiu-nos acelerar os cálculos em outras 1,4 vezes.
Não é tão ruim! Como comparamos até 6 opções de implementação, fornecemos o pseudocódigo do final mais rápido:
: 8- A B, T, T[i] i : res, A B offset ← A 64- effective_len ← , 64- for i from 1 to offset: res ← res + T[xor(A[i] , B[i])] v_a ← 64- , A[offset+1] v_b1 ← 64- , B[offset] v_b2 ← 64- , v_b1 // 64- for i from offset to effective_len: v_b ← align(v_b1, v_b2) // 64- , v_a res ← res + popcnt64(xor(v_a, v_b)) v_a ← 64- v_b1 ← v_b2 v_b2 ← 64- //
Seria ótimo, de uma vez por todas, acelerar o cálculo da distância de Hamming em 11,5 vezes, mas na vida tudo é um pouco mais complicado: essa implementação terá uma vantagem apenas com comprimentos de matrizes suficientemente grandes. Na Fig. A Figura 4 apresenta uma comparação do tempo de cálculo usando a tabela de valores pré-calculados e nossa implementação final. Você pode ver que, com a nossa versão, ela começa a ganhar apenas começando com comprimentos superiores a 400 bytes, e isso também precisa ser levado em consideração ao otimizar a Elbrus.
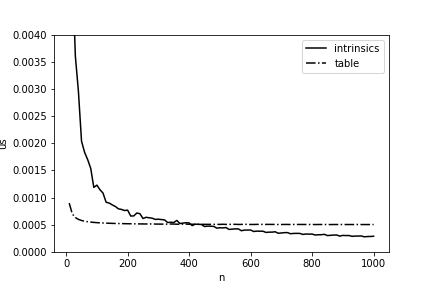
Figura 4 - Tempo médio (por 1 byte) para o cálculo da distância de Hamming entre duas matrizes, dependendo do comprimento em Elbrus-4C.
Isso é tudo, agora estamos prontos para medir o tempo de operação de todo o sistema. Medimos o tempo médio de processamento de solicitações (excluindo o carregamento de imagens) para 933 solicitações. Ao compilar uma descrição compacta da imagem, foi utilizado um descritor binário tipo RFD colorido de 5328 bits. Consistia em 3 descritores de RFD cinza 1776 bits concatenados, calculados para cada canal da seção de imagem de entrada. Por um lado, esses descritores longos não agradam com uma alta velocidade de cálculo e comparação; por outro, fornecem uma qualidade de trabalho suficientemente alta. No entanto, há boas notícias - podemos usar a rápida implementação da distância de Hamming para compará-las! Os comprimentos das matrizes comparadas são 666 bytes, mais do que o valor limite de 400 bytes para o Elbrus-4C.
Os resultados da medição são mostrados na Tabela 2. É possível observar que apenas uma implementação rápida da distância de Hamming fornece um processamento de consulta 1,5 vezes mais rápido. Também é importante notar que essa otimização não altera os resultados dos cálculos e, portanto, a qualidade do reconhecimento.
Tabela 2. Tempo médio de processamento de uma solicitação para um sistema de reconhecimento de objetos de pintura em condições não controladas.
| Um experimento | Hora da solicitação, s | O cálculo da distância de Hamming levou | Tempos de aceleração |
|---|
| Implementação básica | 2,81 | 63% | - |
| Implementação rápida | 1,87 | 40% | 1.5 |
Conclusão
Neste artigo, conversamos um pouco sobre a estrutura do sistema de reconhecimento para pintar objetos em condições descontroladas e mais uma vez mostramos como manipulações de baixo nível podem aumentar significativamente sua velocidade na plataforma Elbrus. Portanto, a implementação proposta da distância de Hamming funciona em uma ordem de magnitude (!) Mais rápida que a implementação, usando uma tabela de valores pré-calculados com um comprimento suficientemente grande dos vetores de entrada, e todo o sistema foi acelerado por um fator de 1,5! Para alcançar esse resultado, foram utilizadas extensões SIMD e os recursos de arquitetura e acesso à memória dos processadores Elbrus-4C e Elbrus-8C foram levados em consideração. Esses resultados mostram que os processadores Elbrus contêm recursos significativos para uma operação eficiente, que não são totalmente utilizados na ausência de otimização especialmente realizada. No entanto, espera-se que os métodos de acesso à memória sejam aprimorados nos processadores Elbrus mais novos, o que permitirá que algumas dessas otimizações sejam executadas automaticamente e facilitará bastante a vida dos desenvolvedores.
Literatura
[1] N.S. Skoryukina, A.N. Milovzorov, D.V. Field, V.V. Arlazarov. O método de reconhecimento de objetos de pintura em condições não controladas com treinamento de acordo com um exemplo // Transações do ISA RAS. - Edição especial, 2018 - p. 5-15.
[2] Pérez-Sanagustín M. et al. Usando códigos QR para aumentar o envolvimento do usuário em espaços semelhantes a museus // Computers in Human Behavior. - 2016. - T. 60. - S. 73-85. doi: 10.1016 / j.chb.2016.02.02.012
[3] Antoshchuk S. G., Godovichenko N. A. Análise das características pontuais da imagem no sistema Mobile Virtual Guide // Pratsi. - 2013. - Não. 1 (40). - 67-72.
[4] Andreatta C., Leonardi F. Reconhecimento de pinturas com base em aparência para um guia móvel de museu // Conferência Internacional sobre Teoria e Aplicações da Visão Computacional, VISAPP. - 2006.
[5] Leonard Wein. 2014. Reconhecimento visual em aplicativos de guias de museus: os visitantes querem isso? .. Nos Anais da Conferência SIGCHI sobre Fatores Humanos em Sistemas de Computação (CHI '14). ACM, Nova Iorque, NY, EUA, 635-638.
doi: 10.1145 / 2556288.2557270
[6] Galeria Tretyakov, https://www.tretyakovgallery.ru/collection/.
[7] Lukoyanov A. S., Nikolaev D. P., Konovalenko I. A. Modificação do algoritmo YAPE para imagens com uma grande disseminação de contraste local // Tecnologias da informação e nanotecnologias. - 2018-- S. 1193-1204.
[8] Muja M., Lowe DG Correspondência rápida de recursos binários // Computer and Robot Vision (CRV), Nona conferência de 2012 em. - IEEE, 2012 - S. 404-410.
doi: 10.1109 / CRV.2012.60
[9] Skoryukina, N., Nikolaev, DP, Sheshkus, A., Polevoy, D. (2015, fevereiro). Detecção de documento retangular em tempo real em dispositivos móveis. Na Sétima Conferência Internacional sobre Visão de Máquina (ICMV 2014) (Vol. 9445, p. 94452A). Sociedade Internacional de Óptica e Fotônica.
doi: 10.1117 / 12.2181377
[10] Kim A.K., Bychkov I.N. e outras tecnologias russas "Elbrus" para computadores pessoais, servidores e supercomputadores // Tecnologias modernas de informação e educação em TI, M.: Fundação para o desenvolvimento da mídia na Internet, educação em TI, potencial humano "League of Internet Media", 2014, 10, p. 39-50.
[11] Kim A.K., Perekatov V.I., Ermakov S.G. Microprocessadores e sistemas de computação
a família Elbrus. - São Petersburgo: Peter, 2013 - 272 S.