Como o PageRank funciona: implementando em R via álgebra linear e o método de potência

Olá, cidadãos de Habrovsk!

Meu nome é Alex. Desta vez, eu transmito do local de trabalho no ITAR-TASS.

Neste breve texto, apresentarei o método de cálculo do PageRank © (a seguir denominado PR) usando exemplos simples e compreensíveis, na linguagem R. O algoritmo é uma propriedade intelectual do Google, mas, devido à sua utilidade para tarefas de análise de dados, muitas tarefas são usadas , que pode ser reduzido à pesquisa de nós grandes no gráfico e à classificação por importância.

Mencionar uma grande empresa em um post não é um anúncio.

Como não sou um matemático profissional, uso - e recomendo a você - este artigo e este tutorial como guia.

Compreensão intuitiva do PR

Compreender como isso funciona não é difícil. Há um conjunto de elementos que estão interconectados. Eis como exatamente eles estão conectados - essa é uma pergunta ampla: talvez por meio de links (como o Google), talvez por referências uns aos outros (quase os mesmos links), as probabilidades de transições entre elementos (matriz do processo de Markov) possam ser especificadas a priori sem especificar o físico significado da comunicação. Eu gostaria de atribuir a esses elementos um certo critério de importância, o qual conteria informações sobre a probabilidade de esse elemento ser visitado por alguma partícula abstrata que viaja pelo gráfico no processo de difusão.

Hum, isso não parece muito claro. É mais fácil imaginar um cara usando um laptop com uma papoula , navegando nas páginas dos resultados de pesquisa, fumando um cachimbo de água, seguindo links de uma página para outra e cada vez mais aparecendo na mesma página (ou páginas).

Isso se deve ao fato de que algumas páginas que ele visita contêm informações tão interessantes na fonte original que outras são forçadas a reimprimi-las com uma indicação do link.

Um cara do Google foi nomeado surfista aleatório. Ele é uma partícula no processo de difusão: uma discreta mudança de posição no gráfico ao longo do tempo. E a probabilidade com que ele visita a página com um tempo de difusão tendendo ao infinito é PR.

Implementação simples do cálculo de RP

Vamos concordar - trabalhamos com 10 elementos, em um gráfico tão pequeno e acolhedor.

# clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark) 

Cada um dos 10 elementos (nós) contém de 10 a 14 referências a outros nós em uma ordem aleatória, excluindo-se. No momento, apenas decidimos que os dados mencionados são um link da web.

É claro que pode acontecer que algum elemento seja mencionado com mais frequência do que outros. Veja isso.

A propósito, eu recomendo usar o pacote data.table para experimentos. Em conjunto com os princípios da arrumação, tudo acontece de forma eficiente e rápida.

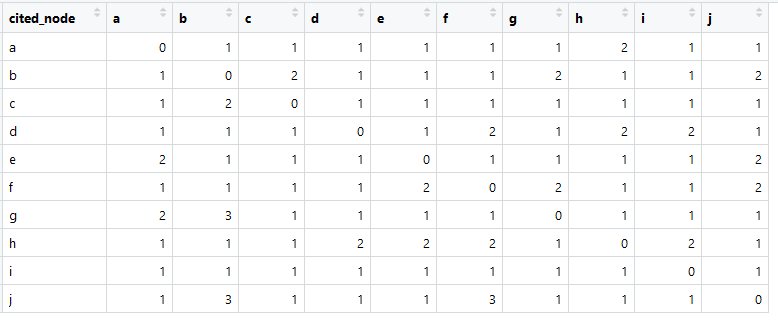
É assim que a nossa matriz de links se parece (chamada em inglês geralmente a matriz de adjacência).

A soma em cada coluna é maior que zero, o que significa que há uma conexão de cada elemento com outro elemento (isso é importante para análises posteriores).

> aplicar (dt [, - 1, com = F], 2, soma)
abcdefghij
11 14 10 10 11 13 11 11 11 12

Com base nessa tabela, podemos criar a chamada matriz de afinidade, ou, em nossa opinião, a matriz de proximidade (e também é chamada de matriz de transição), que os matemáticos chamam de matriz estocástica (matriz estocástica de coluna): fonte principal

Atribua-o a uma variável chamada A.



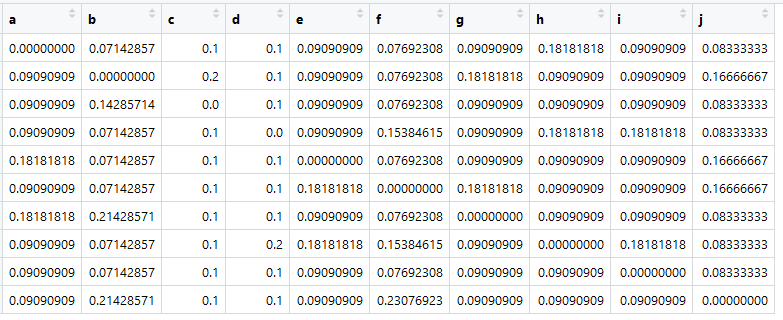
O mais importante agora é que a soma em todas as colunas seja igual a uma.

> colSums (A)
abcdefghij
1 1 1 1 1 1 1 1 1 1 1

Aqui está - uma matriz de transições, é Markov, são semelhanças. As figuras são as probabilidades de transições de um elemento em uma coluna para um elemento em uma linha.

Naturalmente, essas não são "semelhanças" reais. O presente seria, por exemplo, se calcularmos o cosseno do ângulo entre a apresentação dos documentos. Mas é importante que a matriz de transição seja reduzida a (pseudo-) probabilidades, para que a soma de cada coluna seja igual a uma.

Vejamos o gráfico de transição de Markov (nosso A):



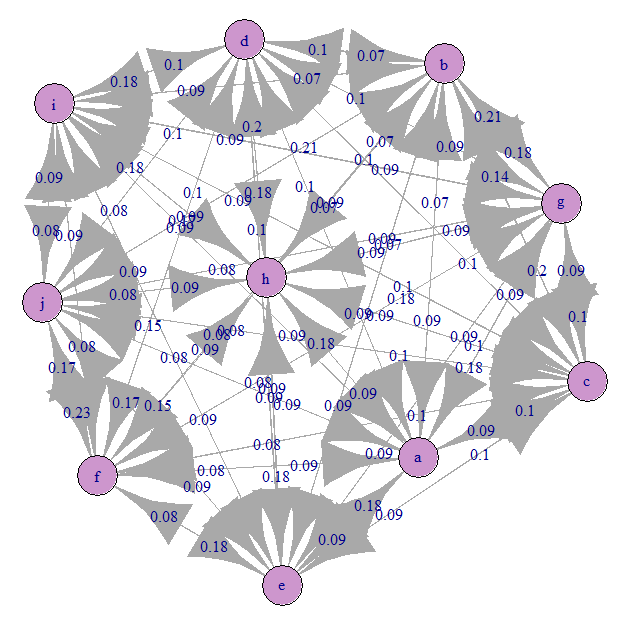
Tudo é aproximadamente igualmente confuso). Isso ocorre porque especificamos transições equiprobáveis.

E agora é a hora da mágica!

 ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2)) 

Para uma matriz estocástica A, o primeiro valor próprio deve ser igual à unidade e o vetor próprio correspondente é o vetor PageRank.

> impressão (redonda (pr, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11

Esse é o vetor dos valores de PR - este é o vetor próprio normalizado da matriz de transição A correspondente ao valor próprio dessa matriz igual à unidade - o vetor próprio dominante.

Agora você pode classificar os elementos. Mas, devido às especificidades do experimento, eles têm um peso muito semelhante.

Problemas e suas soluções usando o método de potência

A matriz de transição A pode não satisfazer as condições de estocástica.

Primeiro, pode haver elementos que não se referem a lugar algum, ou seja, com a ausência de feedback (eles podem se referir a eles mesmos). Para grandes gráficos reais, esse é um problema provável. Isso significa que uma das colunas da matriz terá apenas zeros. Nesse caso, a solução através de vetores próprios não funcionará.

O Google resolveu esse problema preenchendo uma coluna com uma distribuição de probabilidade uniforme p = 1 / N. Onde N é o número de todos os elementos.

 dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) 

Em segundo lugar, o gráfico pode conter elementos com feedback um para o outro, mas não os elementos restantes do gráfico. Esse também é um problema intransponível para álgebra linear devido à violação de suposições.

Isso é resolvido através da introdução de uma constante chamada fator de amortecimento, que indica a probabilidade a priori de uma transição de um elemento para outro, mesmo que não haja links físicos. Em outras palavras, a difusão é possível em qualquer estado.

 d = 0.15 #damping factor (to ensure algorithm convergence) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix 

Se aplicarmos essas transformações à nossa matriz, ela poderá ser resolvida novamente por meio de vetores próprios!

Em terceiro lugar, a matriz brega pode não ser quadrada, mas isso é crítico! Não vou me debruçar sobre este momento, porque acredito que você mesmo descobrirá como consertá-lo.

Mas existe um método mais rápido e preciso, que também é mais econômico na memória (que pode ser relevante para gráficos grandes): Método de potência.

 ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names 

Voila!

> impressão (redonda (pr, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11
> print (redondo (pr2, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11

Nisto terminarei o tutorial. Espero que você ache útil.

Esqueci de dizer que, para construir uma matriz de transições (probabilidades), você pode usar a semelhança de textos, o número de referências, o fato de um link e outras métricas que levam a pseudo-probabilidades ou são probabilidades. Um exemplo bastante interessante é a classificação das sentenças no texto na matriz de similaridade dos sacos de palavras tf-idf para destacar a frase que resume o texto inteiro. Pode haver outros usos criativos do PR.

Eu recomendo tentar por conta própria brincar com a matriz de transição e garantir valores legais de RP, que também são fáceis de interpretar.

Se você vir imprecisões ou erros comigo - indique nos comentários ou na mensagem e eu corrigirei tudo.

Todo o código é compilado aqui:


PS: toda essa ideia também é facilmente implementada em outras linguagens, pelo menos em Python, fiz tudo sem dificuldade.