Como o código de barras é organizado?

Olá Habr!

Uma pessoa moderna encontra códigos de barras todos os dias, sem sequer pensar nisso. Quando compramos produtos no supermercado, seus códigos são lidos precisamente com a ajuda de um código de barras. Também encomendas, mercadorias em armazéns e assim por diante. No entanto, poucas pessoas sabem como isso realmente funciona.

Como o código de barras é organizado e o que é codificado nesta figura?



Vamos tentar descobrir, ao mesmo tempo, escreveremos um decodificador desses códigos.

1. Introdução

O uso de códigos de barras tem uma longa história. As primeiras tentativas de automação começaram nos anos 50; uma patente para um leitor de código foi obtida em 1952. O engenheiro envolvido na triagem de carros na estrada de ferro queria simplificar o processo. A idéia era óbvia - codificar o número usando tiras e lê-las usando fotocélulas. Em 1962, os códigos começaram a ser oficialmente usados ​​para identificar carros nas ferrovias americanas (sistema KarTrak ). Em 1968, o holofote foi substituído por um raio laser, o que aumentou a precisão e reduziu o tamanho do leitor. Em 1973, o formato “Universal Product Code” apareceu e, em 1974, o primeiro produto foi vendido usando um scanner de código (a goma de mascar da Wrigley são os Estados Unidos;) em um supermercado. Em 1984, um terço das lojas usavam serpentinas, mas na Rússia começaram a ser usadas nos anos 90.

Muitos códigos diferentes são usados ​​para tarefas diferentes, por exemplo, a sequência "12345678" pode ser representada de tais maneiras (e isso não é tudo):



Vamos começar a análise bit a bit. Além disso, tudo descrito abaixo se refere ao formulário “Code-128” - simplesmente porque seu formato é bastante simples e direto. Aqueles que desejam experimentar outras espécies podem abrir um gerador on - line e ver por si mesmos.

À primeira vista, o código de barras parece ser apenas uma sequência aleatória de linhas; de fato, sua estrutura é claramente fixa:



1 - Espaço vazio necessário para identificar claramente o início do código
2 - Iniciar símbolo. Para o Código 128, são possíveis três opções (chamadas A, B e C): 11010000100, 11010010000 ou 11010011100, elas correspondem a diferentes tabelas de códigos (mais na Wikipedia ).
3 - Na verdade, o código que contém os dados que precisamos
4 - soma de verificação
5 - Pare o símbolo. Para o Code-128, é 1100011101011.
6 (1) - espaço vazio.

Agora, sobre como os bits são codificados. Tudo é muito simples aqui - se você considerar a largura da linha mais fina como "1", a linha de largura dupla fornecerá o código "11", um "111" triplo e assim por diante. O espaço vazio será "0" ou "00" ou "000" de acordo com o mesmo princípio. Quem desejar pode comparar o código de início na imagem para garantir que a regra seja cumprida.

Agora você pode começar a programar.

Obter a sequência de bits

Em princípio, esta é a parte mais difícil e, é claro, algoritmicamente, pode ser implementada de maneiras diferentes. Não tenho certeza de que o algoritmo abaixo seja ideal, mas é o suficiente para um estudo de caso.

Para começar, carregue a imagem, estique-a em largura, pegue uma linha horizontal no meio da imagem, converta-a em preto e branco e carregue-a como uma matriz.

from PIL import Image import numpy as np import matplotlib.pyplot as plt image_path = "barcode.jpg" img = Image.open(image_path) width, height = img.size basewidth = 4*width img = img.resize((basewidth, height), Image.ANTIALIAS) hor_line_bw = img.crop((0, int(height/2), basewidth, int(height/2) + 1)).convert('L') hor_data = np.asarray(hor_line_bw, dtype="int32")[0] 

No código de barras, “1” corresponde a preto e, em RGB, pelo contrário, 0, portanto, a matriz deve ser invertida. Ao mesmo tempo, calculamos o valor médio.

 hor_data = 255 - hor_data avg = np.average(hor_data) plt.plot(hor_data) plt.show() 

Iniciamos o programa para garantir que o código de barras esteja carregado corretamente:



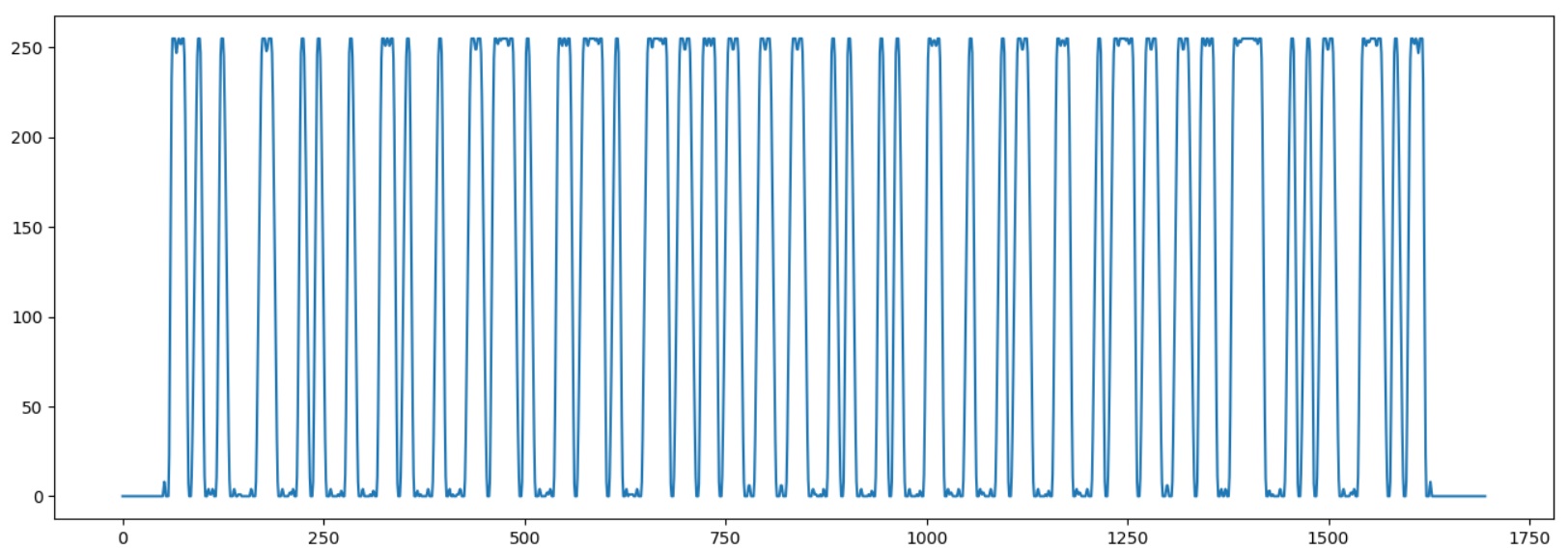
Agora você precisa determinar a largura de um "bit". Para isso, destacamos o início da sequência inicial "1101", registrando os momentos de transição do gráfico pela linha do meio.

 pos1, pos2 = -1, -1 bits = "" for p in range(basewidth - 2): if hor_data[p] < avg and hor_data[p + 1] > avg: bits += "1" if pos1 == -1: pos1 = p if bits == "101": pos2 = p break if hor_data[p] > avg and hor_data[p + 1] < avg: bits += "0" bit_width = int((pos2 - pos1)/3) 

Registramos apenas as transições no meio, para que o código "1101" seja escrito como "101", mas isso é suficiente para descobrirmos sua largura em pixels.

Agora a decodificação real. Encontramos a próxima transição pelo meio e determinamos o número de bits que caem no intervalo. Como a correspondência não é absoluta (o código pode ser ligeiramente curvado ou esticado), usamos o arredondamento.

 bits = "" for p in range(basewidth - 2): if hor_data[p] > avg and hor_data[p + 1] < avg: interval = p - pos1 cnt = interval/bit_width bits += "1"*int(round(cnt)) pos1 = p if hor_data[p] < avg and hor_data[p + 1] > avg: interval = p - pos1 cnt = interval/bit_width bits += "0"*int(round(cnt)) pos1 = p 

Não tenho certeza se essa é a melhor opção, talvez exista uma maneira melhor, quem quiser pode escrever nos comentários.

Se tudo foi feito corretamente, obtemos a seguinte sequência de saída:

11010010000110001010001000110100010001101110100011011101000111011011
01100110011000101000101000110001000101100011000101110110011011001111
00010101100011101011

Decodificação

Aqui, em princípio, não há dificuldades. Os caracteres no Código 128 são codificados com um código de 11 bits, que possui três variedades (A, B e C) e pode armazenar codificações ou números diferentes de caracteres de 00 a 99.

No nosso caso, o início da sequência é 11010010000, que corresponde ao "Código B". Ele foi terrivelmente quebrado para conduzir manualmente todos os códigos da Wikipedia, portanto a tabela foi simplesmente copiada do navegador e sua análise também foi feita em Python (dica: isso não é necessário para a produção).

  CODE128_CHART = """ 0 _ _ 00 32 S 11011001100 212222 1 ! ! 01 33 ! 11001101100 222122 2 " " 02 34 " 11001100110 222221 3 # # 03 35 # 10010011000 121223 ... 93 GS } 93 125 } 10100011110 111341 94 RS ~ 94 126 ~ 10001011110 131141 103 Start Start A 208 SCA 11010000100 211412 104 Start Start B 209 SCB 11010010000 211214 105 Start Start C 210 SCC 11010011100 211232 106 Stop Stop - - - 11000111010 233111""".split() SYMBOLS = [value for value in CODE128_CHART[6::8]] VALUESB = [value for value in CODE128_CHART[2::8]] CODE128B = dict(zip(SYMBOLS, VALUESB)) 

Agora a coisa mais simples permanece. Dividimos nossa sequência de bits em blocos de 11 caracteres:

 sym_len = 11 symbols = [bits[i:i+sym_len] for i in range(0, len(bits), sym_len)] 

Finalmente, formamos a linha e a exibimos na tela:

 str_out = "" for sym in symbols: if CODE128A[sym] == 'Start': continue if CODE128A[sym] == 'Stop': break str_out += CODE128A[sym] print(" ", sym, CODE128A[sym]) print("Str:", str_out) 

Não darei a resposta para o que está codificado na tabela, que seja lição de casa para os leitores (usar programas prontos para smartphones será considerado trapaça).

O código também não implementa a verificação CRC, aqueles que desejam podem fazer isso sozinhos.

Obviamente, o algoritmo é imperfeito e foi escrito em meia hora. Para fins mais profissionais, existem bibliotecas prontas, por exemplo, pyzbar . O código usando essa biblioteca terá apenas 4 linhas:

 from pyzbar.pyzbar import decode img = Image.open(image_path) decode = decode(img) print(decode) 

(primeiro você precisa instalar a biblioteca digitando o comando pip install pyzbar)

Adição : vinograd19 escreveu nos comentários sobre a contagem de CRC:

A história do dígito de verificação é interessante. Surgiu evolutivamente.
O dígito de verificação é necessário para evitar decodificação incorreta. Se o código de barras era 1234 e foi reconhecido como 7234, você precisa de uma validação que impeça a substituição de 1 por 7. A validação pode ser imprecisa para que pelo menos 90% dos números inválidos sejam determinados com antecedência.

1ª abordagem: vamos pegar a quantia. Para que o restante da divisão por 10 seja 0. Bem, ou seja, os 12 primeiros caracteres carregam uma carga de informações e o último dígito é selecionado para que a soma dos dígitos seja dividida por 10. Decodifique a sequência, se a soma não for divisível por dez, significa decodificada com um erro e você precisa fazer isso mais uma vez. Por exemplo, o código 1234 é válido. 1 + 2 + 3 + 4 = 10. O código 1216 também é válido, mas 1218 não é.

Isso evita problemas com a automação. No entanto, no momento da criação dos códigos de barras, houve um fallback na forma de digitar um número nas teclas. E há um caso ruim: se você alterar a ordem dos dois dígitos, a soma de verificação não muda, e isso é ruim. Ou seja, se o código de barras 1234 foi martelado como 2134, a soma de verificação convergirá, mas inserimos o número errado. Acontece que a ordem errada dos números é um caso comum se você pressionar as teclas rapidamente.

2ª abordagem. Bem, vamos tornar a quantia um pouco mais complicada. Para que os números em lugares pares sejam levados em consideração duas vezes. Então, ao alterar a ordem, o valor definitivamente não convergirá para o desejado. Por exemplo, o código 2364 é válido (2 + 3 + 3 + 6 + 4 + 4 = 20) e o código 3264 é inválido (3+ 2 + 2 + 6 + 4 + 4 = 19). Mas aqui estava outro exemplo ruim de dirigir. Alguns teclados são de tal ordem que dez dígitos são organizados em duas linhas. a primeira linha é 12345 e, abaixo dela, a segunda segunda linha é 67890. Se, em vez da tecla "1", pressione a tecla "2" à direita, a soma de verificação impedirá a entrada incorreta. Mas se, em vez da tecla "1", pressione a tecla "6" abaixo, ela poderá não avisar. Afinal, 6 = 1 + 5, e no caso em que esse número esteja em um local par ao calcular a soma de verificação, temos 2 * 6 = 2 * 1 + 2 * 5. Ou seja, a soma de verificação aumentou exatamente 10, portanto, seu último dígito não foi alterado. Por exemplo, as somas de verificação nos códigos 2134 e 2634 são iguais. O mesmo erro ocorrerá se pressionarmos 7 em vez de 2, em vez de 3, pressionar 8 e assim por diante.

3ª abordagem. Ok, vamos pegar a soma novamente, apenas os números em lugares pares serão levados em conta ... três vezes. Ou seja, o código 1234565 é válido, porque 1 + 2 * 3 + 3 + 4 * 3 + 5 + 6 * 3 +5 = 50.

O método descrito tornou-se o padrão para o cálculo da soma de verificação EAN13 com algumas correções: o número de dígitos tornou-se fixo e igual a 13, onde o 13º é a mesma soma de verificação. Os números em lugares ímpares são contados três vezes, nos pares - uma vez.

Conclusão

Como você pode ver, mesmo uma coisa simples como um código de barras tem muitas coisas interessantes. A propósito, outro truque para quem já leu até aqui - o texto sob o código de barras (se houver) duplica completamente seu conteúdo. Isso é feito para que, em caso de código ilegível, o operador possa digitá-lo manualmente. Portanto, para descobrir o conteúdo de um código de barras geralmente é simples - basta olhar para o texto abaixo.

Como sugerido nos comentários, o mais popular no comércio é o código EAN-13, a codificação de bits é a mesma, e aqueles que desejam podem ver a estrutura dos caracteres.

Se os leitores não perderem o interesse, considere os códigos QR separadamente.

Obrigado pela atenção.