♻️ 🚞 🙆🏾 Aprendizado profundo de reforço: pingue-pongue de pixel bruto 🐎 ✋🏿 🤴

Este é um artigo muito atrasado sobre o aprendizado por reforço (RL). RL é um tópico interessante!

Você pode saber que os computadores agora podem aprender automaticamente a jogar jogos da ATARI (obtendo pixels brutos do jogo na entrada!). Eles venceram os campeões mundiais no jogo Go , aprendem virtual de quatro patas a correr e pular , e os robôs aprendem a executar tarefas complexas de manipulação que desafiam a programação explícita. Acontece que todas essas conquistas não são completas sem a RL. Também fiquei interessado em RL no ano passado: trabalhei com o livro de Richard Sutton (aprox. Referência: substituído) , li o curso de David Silver , assisti às palestras de John Schulman , escrevi a biblioteca RL em Javascript e estagiei no DeepMind no verão, trabalhando em um grupo O DeepRL e, mais recentemente, no desenvolvimento do OpenAI Gym , é o novo kit de ferramentas RL. Por isso, é claro, estou nessa onda há pelo menos um ano, mas ainda não me preocupo em escrever uma nota sobre por que a RL é de grande importância, sobre o que é, como tudo se desenvolve.

Exemplos de uso do Deep Q-Learning. Da esquerda para a direita: a rede neural joga ATARI, a rede neural joga AlphaGo, o robô dobra Lego, o virtual quadrúpede corre em volta de obstáculos virtuais.

É interessante refletir sobre a natureza do progresso recente na RL. Gostaria de observar quatro fatores separados que afetam o desenvolvimento da IA:

Velocidade de computação (GPU, dispositivos especiais ASIC, lei de Moore)
Dados suficientes em um formato utilizável (por exemplo, ImageNet)
Algoritmos (pesquisa e ideias, por exemplo, backprop, CNN, LSTM)
Infraestrutura (Linux, TCP / IP, Git, ROS, PR2, AWS, AMT, TensorFlow, etc.).

Assim como na visão computacional, o progresso na RL está se movendo ... embora não tanto quanto possa parecer. Por exemplo, na visão computacional, a rede neural AlexNet 2012 é uma versão aumentada em profundidade e largura da rede neural ConvNets dos anos 90. Da mesma forma, o ATARI Deep Q-Learning 2013 é uma implementação do algoritmo Q-Learning padrão que você pode encontrar no livro clássico de Richard Sutton, de 1998. Além disso, o AlphaGo usa a técnica Gradiente de política e a pesquisa em árvore Monte Carlo (MCTS) também são idéias antigas ou suas combinações. Obviamente, são necessárias muitas habilidades e paciência para fazê-las funcionar, e muitas configurações complicadas foram desenvolvidas com base em algoritmos antigos. Mas, em uma primeira aproximação, o principal fator do progresso recente não são novos algoritmos e idéias, mas a intensificação de cálculos, dados suficientes e infraestrutura madura.

Agora de volta à RL. Muitas pessoas não acreditam que podemos ensinar um computador a jogar jogos da ATARI em nível humano usando pixels brutos do zero e usando o mesmo algoritmo de auto-aprendizado. Ao mesmo tempo, toda vez que sinto uma lacuna - como parece mágico e como é realmente simples por dentro.

A abordagem básica que usamos é realmente muito burra. Seja como for, gostaria de apresentar a técnica Policy Gradient (PG), nossa opção padrão favorita para resolver problemas com RL no momento. Você pode estar curioso por que, em vez disso, não consigo imaginar o DQN, que é um algoritmo RL alternativo e mais conhecido que também é usado no treinamento da ATARI . Acontece que, embora o Q-Learning seja conhecido, ele não é tão perfeito. A maioria das pessoas escolhe usar o Policy Gradient, incluindo os autores do artigo original do DQN , que mostraram que, com um bom ajuste, o Policy Gradient funciona ainda melhor que o Q-Learning. O PG é preferível porque é explícito: existe uma política clara e uma abordagem coerente que otimiza diretamente as recompensas esperadas. Como exemplo, aprenderemos como jogar o ATARI Pong: do zero, de pixels brutos por meio de um Gradiente de Política com uma rede neural. E colocaremos tudo isso em 130 linhas de Python. ( Link Gist ) Vamos ver como isso é feito.

Acima: Ping Pong. Abaixo: Apresentação de pingue-pongue como um caso especial do processo de tomada de decisão de Markov (MDP) : Cada vértice do gráfico corresponde a um determinado estado do jogo, e as bordas determinam as probabilidades de transição para outros estados. Cada costela também determina a recompensa. O objetivo é encontrar o melhor caminho de qualquer estado para maximizar a recompensa

Jogar Ping Pong é um ótimo exemplo de desafio de RL. Na versão ATARI 2600, jogaremos uma raquete. Outra raquete é controlada por um algoritmo embutido. Precisamos bater na bola para que o outro jogador não tenha tempo de bater nela. Espero que não seja necessário explicar o que é o Ping Pong. Em um nível baixo, o jogo funciona da seguinte maneira: obtemos um quadro de imagem - uma matriz de bytes 210x160x3 e decidimos se queremos mover a raquete PARA CIMA ou PARA BAIXO. Ou seja, temos apenas duas opções para gerenciar o jogo. Após cada escolha, o simulador de jogo executa sua ação e nos dá uma recompensa: +1 em recompensa se a bola passou na raquete do oponente ou -1 em se perdemos a bola. Caso contrário, 0. E, é claro, nosso objetivo é mover a raquete para obter a maior recompensa possível.

Ao considerar uma solução, lembre-se de que tentaremos fazer tão poucas suposições sobre o pong, porque isso não é particularmente importante na prática. Levamos muito mais em conta em tarefas de grande escala, como manipulação de robôs, montagem e navegação. Pong é apenas um divertido caso de teste de brinquedo com o qual brincamos enquanto descobrimos como escrever sistemas de IA muito gerais que podem um dia executar tarefas úteis arbitrárias.

Rede neural como uma política de RL . Em primeiro lugar, determinaremos a política que nosso jogador (ou "agente") implementa. ((*) "Agente", "ambiente" e "política do agente" são termos padrão da teoria da RL). A função política no nosso caso é uma rede neural. Ela aceitará o estado do jogo na entrada e na saída ela decidirá o que fazer - subir ou descer. Como nosso bloco de cálculo simples favorito, usaremos uma rede neural de duas camadas que obtém pixels brutos da imagem (total de 100.800 números (210 * 160 * 3)) e produz um único número indicando a probabilidade de mover a raquete para cima. Observe que o uso de política estocástica é padrão, o que significa que produzimos apenas a probabilidade de movimento ascendente. Para obter a mudança real, usaremos essa probabilidade. A razão para isso ficará mais clara quando falarmos sobre treinamento.

Nossa função política consiste em uma rede neural totalmente conectada em duas camadas

Mais especificamente, suponha que na entrada recebamos um vetor X, que contém um conjunto de pixels pré-processados. Então devemos calcular usando python \ numpy:

h = np.dot(W1, x) # compute hidden layer neuron activations h[h<0] = 0 # ReLU nonlinearity: threshold at zero logp = np.dot(W2, h) # compute log probability of going up p = 1.0 / (1.0 + np.exp(-logp)) # sigmoid function (gives probability of going up)

Nesse fragmento, W1 e W2 são duas matrizes que inicializamos aleatoriamente. Nós não usamos preconceitos, porque queríamos. Note que no final usamos a não linearidade do sigmóide, o que reduz a probabilidade de saída para o intervalo [0,1]. Intuitivamente, os neurônios em uma camada oculta (cujos pesos estão localizados em W1) podem detectar vários cenários de jogo (por exemplo, a bola está no topo e nossa raquete está no meio), e os pesos no W2 podem decidir se devemos subir em cada caso ou para baixo. As combinações aleatórias iniciais W1 e W2, é claro, a princípio causarão espasmos e convulsões em nosso neuro-jogador, o que o iguala a um imbecil-autista nos controles de um avião. Portanto, a única tarefa agora é encontrar W1 e W2, o que leva a um bom jogo!

Há uma observação sobre o pré-processamento de pixels - idealmente, você precisa transferir pelo menos 2 quadros para a rede neural para que ele possa detectar movimento. Mas, para simplificar a situação, aplicaremos a diferença de dois quadros. Ou seja, subtrairemos os quadros atuais e anteriores e só então aplicaremos a diferença à entrada da rede neural.

Parece algo impossível. Neste ponto, gostaria que você apreciasse a complexidade do problema da RL. Obtemos 100 800 números (210x160x 3) e enviamos para nossa rede neural que implementa a política do jogador (que, aliás, inclui facilmente cerca de um milhão de parâmetros nas matrizes W1 e W2). Suponha que em algum momento decidimos subir. O simulador de jogo pode responder que desta vez receberemos 0 prêmios e nos fornecerá outros 100 800 números para o próximo quadro. Podemos repetir esse processo centenas de vezes antes de receber uma recompensa diferente de zero! Por exemplo, suponha que finalmente recebemos uma recompensa +1. Isso é maravilhoso, mas como então podemos dizer - o que levou a isso? Foi essa a ação que fizemos agora? Ou talvez 76 quadros de volta? Ou talvez isso tenha sido associado primeiro ao quadro 10 e depois fizemos algo certo no quadro 90? E como descobrimos - qual dos milhões de "canetas" girar para alcançar um sucesso ainda maior no futuro? Chamamos isso de tarefa de determinar o coeficiente de confiança em certas ações. No caso específico do pong, sabemos que obtemos +1 se a bola passou pelo oponente. A verdadeira razão é que chutamos acidentalmente a bola por um bom caminho alguns quadros atrás, e cada ação subsequente que realizamos não a afetou. Em outras palavras, estamos diante de um problema computacional muito complexo e tudo parece bastante sombrio.

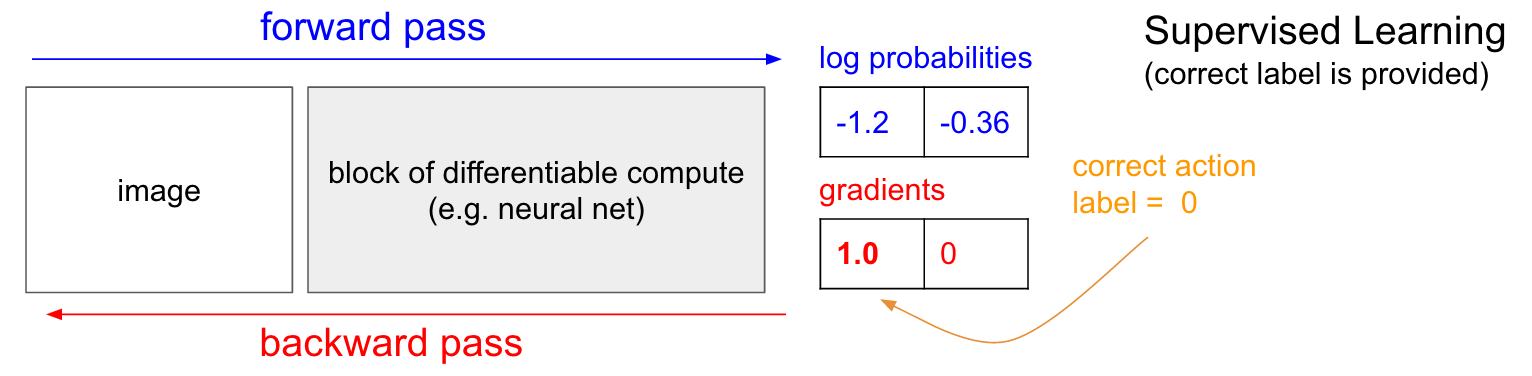
Treinando com um professor. Antes de nos aprofundarmos no gradiente da política (PG), gostaria de relembrar brevemente o ensino com um professor, porque, como veremos, a RL é muito semelhante. Consulte a tabela abaixo. No ensino comum com um professor, transferiremos a imagem para a rede e receberemos na saída algumas probabilidades numéricas para as aulas. Por exemplo, no nosso caso, temos duas classes: UP e DOWN. Uso as probabilidades logarítmicas (-1,2, -0,36) em vez das probabilidades no formato 30% e 70%, porque otimizamos a probabilidade logarítmica da classe (ou etiqueta) correta. Isso torna os cálculos matemáticos mais elegantes e equivale a otimizar apenas a probabilidade, porque o logaritmo é monótono.

Ao treinar com um professor, teremos acesso instantâneo à turma correta (etiqueta). No estágio de treinamento, eles nos dirão exatamente qual o passo certo necessário agora (digamos que seja UP, etiqueta 0), embora a rede neural possa pensar de maneira diferente. Portanto, calculamos o gradiente

é

$\ nabla_ {W} \ log p (y = UP \ médio x)$ para ajustar as configurações de rede. Esse gradiente apenas nos diz como devemos alterar cada um dos milhões de parâmetros para que a rede tenha um pouco mais probabilidade de prever o UP na mesma situação. Por exemplo, um dentre um milhão de parâmetros na rede pode ter um gradiente de -2,1, o que significa que se aumentássemos esse parâmetro por um pequeno valor positivo (por exemplo, 0,001), a probabilidade logarítmica de UP diminuiria em 2,1 * 0,001. (diminuição devido ao sinal negativo). Se aplicarmos o gradiente e atualizarmos o parâmetro usando o algoritmo de retropropagação, sim, nossa rede fornecerá uma alta probabilidade de UP quando vir a mesma imagem ou uma imagem muito semelhante no futuro.

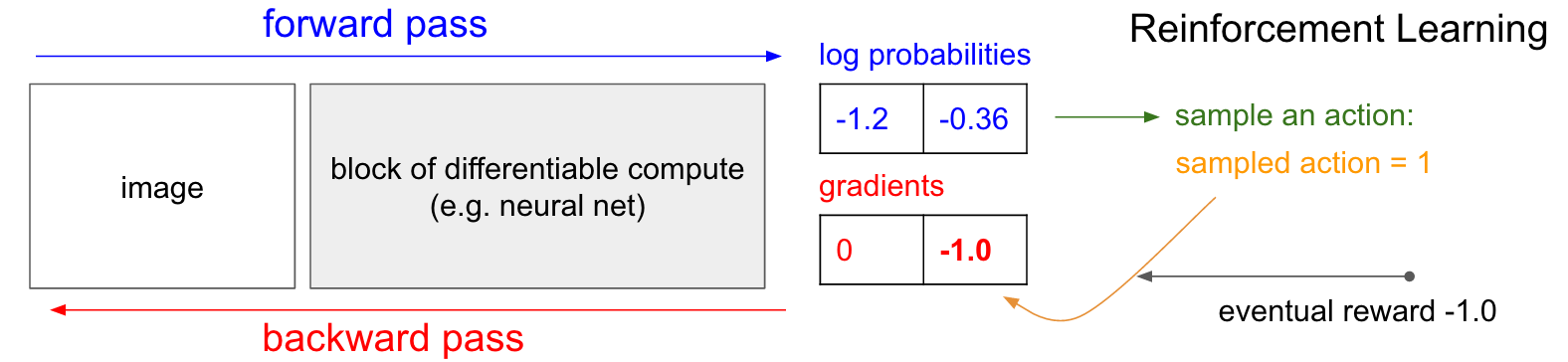
Gradientes de Política (PG) . OK, mas o que fazemos se não tivermos o rótulo de treinamento de reforço correto? Aqui está uma solução para o PG (consulte o diagrama abaixo novamente). Nossa rede neural calculou a probabilidade de um aumento de 30% (logprob -1.2) e de DOWN em 70% (logprob -0.36). Agora, fazemos uma seleção dessa distribuição e especificamos qual ação iremos executar. Por exemplo, eles escolheram DOWN e enviaram essa ação para o simulador de jogo. Nesse ponto, preste atenção a um fato interessante: poderíamos calcular e aplicar imediatamente o gradiente para a ação DOWN, como fizemos no ensino com um professor, e assim aumentar a probabilidade da rede de executar a ação DOWN no futuro. Assim, podemos apreciar e lembrar imediatamente esse gradiente. Mas o problema é que, no momento, ainda não sabemos - é bom descer? Mas o mais interessante é que podemos esperar um pouco e aplicar o gradiente mais tarde! Em Pong, podemos esperar até o final do jogo, receber a recompensa que recebemos (+1 se vencemos ou -1 se perdemos) e inseri-la como um fator para o gradiente. Portanto, se introduzirmos -1 para a probabilidade DOWN e fizermos a propagação reversa, reconstruiremos os parâmetros da rede para que seja menos provável que a ação DOWN seja executada no futuro quando encontrar a mesma imagem, já que a adoção dessa ação nos levou a perder o jogo. Ou seja, precisaremos lembrar de alguma forma todas as ações (entradas e saídas da rede neural) em um episódio do jogo e, com base nessa matriz, torcer a rede neural da mesma maneira que no ensino com um professor.

E é tudo o que é necessário: temos uma política estocástica que escolhe ações e, no futuro, ações que acabam por levar a bons resultados são incentivadas e ações que levam a maus resultados não são incentivadas. Além disso, a recompensa não deve ser de +1 ou -1 se finalmente vencermos o jogo. Pode ser um valor arbitrário com o mesmo significado. Por exemplo, se tudo der certo, a recompensa pode ser 10,0, que usamos como gradiente para iniciar a retropropagação do backprop. Essa é a beleza das redes neurais. Usá-los pode parecer uma farsa: você pode ter 1 milhão de parâmetros embutidos em 1 teraflop de cálculos e pode fazer o programa aprender a fazer coisas arbitrárias com descida do gradiente estocástico (SGD). Não deve funcionar, mas é engraçado vivermos em um universo onde ele funciona.

Se jogássemos jogos de tabuleiro simples, como damas, o pedido seria aproximadamente o mesmo. Há uma diferença notável em relação aos algoritmos de recorte minimax ou alfa-beta. Nesses algoritmos, o programa olha alguns passos à frente, conhecendo as regras do jogo e analisa milhões de posições. Na abordagem RL, apenas movimentos efetivamente feitos são analisados. Ao mesmo tempo, a rede neural não espera, pois não sabe nada sobre as regras do jogo.

Ordem de treino em detalhes. Criamos e inicializamos uma rede neural com alguns W1, W2 e jogamos 100 jogos de pong (chamamos isso de "desentendimento" da política, lançamentos de políticas). Suponha que cada jogo consista em 200 quadros, portanto, no total, tomamos 100 * 200 = 20.000 decisões para subir ou descer. E para cada uma das soluções, conhecemos o gradiente que nos diz como os parâmetros devem mudar se queremos incentivar ou proibir esta solução nesse estado no futuro. Tudo o que resta agora é rotular cada decisão que tomamos como boa ou ruim. Por exemplo, suponha que vencemos 12 jogos e perdemos 88. Tomaremos todas as 200 * 12 = 2400 decisões que tomamos nos jogos vencedores e faremos uma atualização positiva (preenchendo um gradiente de +1,0 para cada ação, executando backprop e atualizando os parâmetros incentivar as ações que escolhemos em todas essas condições). E tomaremos as outras 200 * 88 = 17.600 decisões que tomamos na perda de jogos e faremos uma atualização negativa (não aprovando o que fizemos). E isso é tudo o que preciso. Agora, a rede terá mais chances de repetir ações que funcionaram e um pouco menos provável de repetir ações que não funcionaram. Agora, jogamos outros 100 jogos com nossa nova política ligeiramente aprimorada e repetimos a aplicação de gradientes.

Esquema de desenho animado de 4 jogos. Cada círculo preto é um tipo de estado do jogo (três exemplos de estados são mostrados abaixo) e cada seta é uma transição marcada com a ação que foi selecionada. Nesse caso, vencemos 2 jogos e perdemos 2 jogos. Fizemos os dois jogos que vencemos e incentivamos levemente todas as ações que fizemos neste episódio. Por outro lado, também levaremos os dois jogos perdidos e desencorajaremos ligeiramente cada ação individual que realizamos neste episódio.

Se você refletir sobre isso, começará a encontrar algumas propriedades divertidas. Por exemplo, e se fizéssemos uma boa ação no quadro 50, chutando a bola corretamente, mas perdemos a bola no quadro 150? Como perdemos o jogo, cada ação individual agora é marcada como ruim e isso não impede o acerto correto no quadro 50? Você está certo - será assim para esta festa. No entanto, quando você considera o processo em milhares / milhões de jogos, a execução correta da recuperação aumenta a probabilidade de vitória no futuro. Em média, você verá atualizações mais positivas do que negativas para um golpe de raquete adequado. E a política de implementação de redes neurais produzirá as reações certas.

Atualização: 9 de dezembro de 2016 é uma visão alternativa. Na minha explicação acima, uso termos como "definir uma propagação de gradiente e backprop back", que é uma técnica hábil definida. Se você está acostumado a escrever seu próprio código de backprop espalhado por backprop ou usando o Torch, pode controlar totalmente os gradientes. No entanto, se você está acostumado ao Theano ou ao TensorFlow, ficará um pouco confuso porque o código backprop é totalmente automatizado e difícil de personalizar. Nesse caso, a seguinte visão alternativa pode ser mais produtiva. Ao ensinar com um professor, o objetivo usual é maximizar

$\ sum_i \ log p (y_i \ mid x_i)$ onde

$x_i, y_i$ - exemplos de treinamento (como imagens e seus rótulos). A aplicação do gradiente à função política coincide exatamente com o treinamento com o professor, mas com duas pequenas diferenças: 1) não temos os rótulos corretos

$y_i$ , portanto, como um "rótulo falso", usamos a ação que recebemos para selecionar a política quando viu

$x_i$ e 2) Introduzimos outro coeficiente de conveniência (vantagem) para cada ação. Assim, no final, nossa perda agora parece

$\ sum_i A_i \ log p (y_i \ mid x_i)$ onde

$y_i$ - esta é a ação que realizamos com a amostra, e

$A_i$ É o número que chamamos de coeficiente de conveniência. Por exemplo, no caso de pong, o valor

$A_i$ pode ser 1,0 se acabarmos vencendo o episódio e -1,0 se perdermos. Isso garante que maximizamos a probabilidade de registrar ações que levaram a um bom resultado e minimizamos a probabilidade de registrar ações que não o fizeram. E ações neutras como resultado de muitos apelos não afetarão particularmente a função da política. Assim, o aprendizado por reforço é exatamente o mesmo que aprender com um professor, mas em um conjunto de dados (episódios) em constante mudança, com um fator adicional.

Recursos de viabilidade mais avançados. Também prometi um pouco mais de informação. Até o momento, avaliamos a correção de cada ação individual com base em nossa vitória ou não. Em uma configuração de RL mais geral, receberemos uma "recompensa condicional"

$r_t$ para cada etapa, dependendo do número ou hora da etapa. Uma das opções comuns é usar um coeficiente com desconto, para que a “possível recompensa” no diagrama acima seja

$R_t = \ sum_ {k = 0} ^ {\ infty} \ gama ^ k r_ {t + k}$ onde

$\ gama$ É um número de 0 a 1, chamado coeficiente de desconto (por exemplo, 0,99). A expressão diz que a força com a qual incentivamos a ação é a soma ponderada de todas as recompensas, mas as recompensas subsequentes são exponencialmente menos importantes. Ou seja, cadeias curtas de ações são melhor incentivadas e a cauda de longas cadeias de ações se torna menos importante. Na prática, você também precisa normalizá-los. Por exemplo, suponha que calculamos

$R_t$ para todas as 20.000 ações em uma série de 100 episódios do jogo. Uma boa idéia é normalizar esses valores (subtrair a média, dividir pelo desvio padrão) antes de conectá-los ao algoritmo backprop. Assim, sempre incentivamos e desencorajamos cerca de metade das ações realizadas. Isso reduz as flutuações e torna a política mais convergente. Um estudo mais profundo pode ser encontrado em [ link ].

Derivado de uma função de política. Eu também queria descrever brevemente como os gradientes são feitos matematicamente. Os gradientes da função da política são um caso especial de uma teoria mais geral. O caso geral é que, quando temos uma expressão da forma

$E_ {x \ sim p (x \ mid \ theta)} [f (x)]$ , ou seja, a expectativa de alguma função escalar

$f (x)$ com alguma distribuição de seu parâmetro

$p (x; \ theta)$ parametrizado por algum vetor

$\ theta$ . Então

$f (x)$ se tornará nossa função de recompensa (ou a função de conveniência em um sentido mais geral) e a distribuição discreta

$p (x)$ será a nossa política, que na verdade tem a forma

$p (a \ mid I)$ dando as probabilidades de uma ação a para a imagem

$I$ . Então, estamos interessados em como podemos mudar a distribuição de p através de seus parâmetros

$\ theta$ aumentar

$f$ (ou seja, como alteramos as configurações de rede para que as ações recebam uma recompensa maior). Nós temos isso:

$\ begin {align} \ nabla _ {\ theta} E_x [f (x)] & = \ nabla _ {\ theta} \ sum_x p (x) f (x) & \ text {definição de expectativa} \\ & = \ sum_x \ nabla _ {\ theta} p (x) f (x) e \ text {troque a soma e o gradiente} \\ & = \ sum_x p (x) \ frac {\ nabla _ {\ theta} p (x)} {p (x)} f (x) & \ text {multiplique e divida por} p (x) \\ & = \ sum_x p (x) \ nabla _ {\ theta} \ log p (x) f (x) & \ text {use o fato de que} \ nabla _ {\ theta} \ log (z) = \ frac {1} {z} \ nabla _ {\ theta} z \\ & = E_x [f (x) \ nabla _ {\ theta} \ log p (x)] & \ text {definição de expectativa} \ end {align$

Vou tentar explicar isso. Temos alguma distribuição

$p (x; \ theta)$ (Usei a abreviação

$p (x)$ a partir do qual podemos selecionar valores específicos. Por exemplo, pode ser uma distribuição gaussiana da qual um gerador de números aleatórios é amostrado. Para cada exemplo, também podemos calcular a função de estimativa

$f$ , que, de acordo com o exemplo atual, fornece uma estimativa escalar. A equação resultante nos diz como devemos mudar a distribuição através de seus parâmetros

$\ theta$ se quisermos mais exemplos de ações baseadas nela para obter taxas mais altas

$f$ . Tomamos alguns exemplos de ações

$x$ e sua avaliação

$f (x)$ , e também para cada x, também avaliamos o segundo termo

$\ nabla _ {\ theta} \ log p (x; \ theta)$ . O que é esse multiplicador? Este é precisamente o vetor - o gradiente, que nos dá uma direção no espaço do parâmetro, o que levará a um aumento na probabilidade de uma ação específica

$x$ . Em outras palavras, se empurrássemos θ na direção

$\ nabla _ {\ theta} \ log p (x; \ theta)$ , veremos que a nova probabilidade dessa ação aumentará um pouco. Se você olhar para a fórmula, ela nos diz que devemos tomar essa direção e multiplicar o valor escalar por ela.

$f (x)$ . Isso garantirá que exemplos de ações com uma classificação mais alta (no nosso caso, uma recompensa) sejam "mais atraentes" do que exemplos com um indicador mais baixo; portanto, se formos atualizar com base em várias amostras de

$p$ , a densidade de probabilidade mudaria para a direção de pontos de jogo resultantes mais altos, o que aumenta a probabilidade de obter exemplos de ações com altas recompensas. É importante que o gradiente não seja retirado da função

$f$ , pois geralmente pode ser indiferenciado e imprevisível. Um

$p$ diferenciável por

$\ theta$ . Isso é

$p$ é uma distribuição discreta continuamente ajustável, onde você pode ajustar as probabilidades de ações individuais. Também assumimos que

$p$ normalizado.

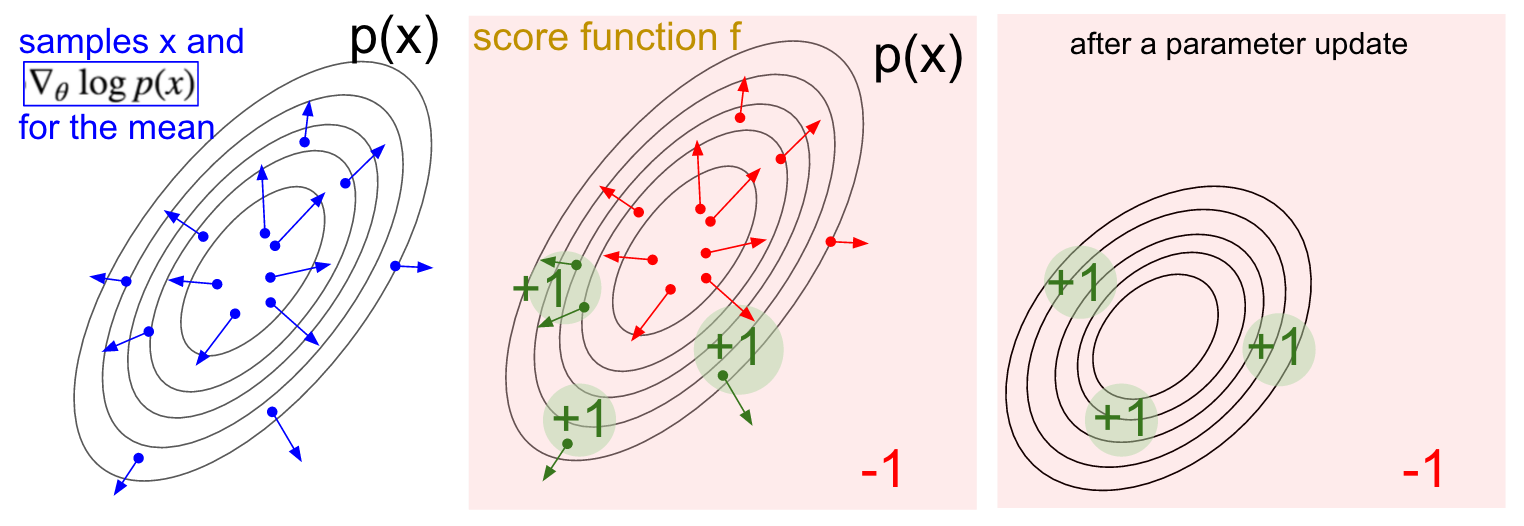Visualização em gradiente. Esquerda: distribuição gaussiana e vários exemplos (pontos azuis). Em cada ponto azul, também plotamos o gradiente da probabilidade logarítmica em relação ao parâmetro médio. A seta indica a direção na qual o valor médio da distribuição deve ser alterado para aumentar a probabilidade dessa ação de exemplo. No meio: Adicionada alguma função de avaliação que fornece -1 em todos os lugares, exceto +1 em algumas regiões pequenas (observe que essa pode ser uma função escalar arbitrária e não necessariamente diferenciável). As setas agora são codificadas por cores, porque, devido à multiplicação, calcularemos a média de todas as setas verdes com uma classificação positiva e as setas vermelhas negativas. Direita: após atualizar os parâmetros, as setas verdes e as setas vermelhas invertidas nos empurram para a esquerda e para baixo. As amostras dessa distribuição agora terão uma classificação esperada mais alta, se desejado.

Espero que a conexão com a RL seja clara.Nossa política nos dá exemplos de ações, e algumas delas funcionam melhor que outras (a julgar pela função da conveniência). A maneira de alterar as configurações da política é executar, pegar o gradiente das ações selecionadas, multiplicá-lo pela classificação e adicionar tudo o que fizemos acima. Para uma conclusão mais completa, recomendo uma palestra de John Shulman.

Treinamento. Bem, desenvolvemos os princípios dos gradientes da função da política. Eu implementei toda a abordagem em um script Python de 130 linhas que usa o emulador ATAI 2600 Pong pronto da OpenAI Gym. Treinei uma rede neural de duas camadas com 200 neurônios da camada oculta usando o algoritmo RMSProp para uma série de 10 episódios (cada episódio pelas regras consiste em vários sorteios de bola e o episódio continua com 21). Não configurei muito os hiper parâmetros e experimentei no meu Macbook lento, mas após um treino de três dias, recebi uma política que é um pouco melhor do que o player embutido. O número total de episódios foi de aproximadamente 8.000, portanto, o algoritmo jogou aproximadamente 200.000 jogos de pong, o que é bastante, e produziu um total de ~ 800 atualizações nos pesos. Se eu treinasse na GPU com ConvNets, em alguns dias conseguiria ótimos resultados e, se otimizasse os hiperparâmetros, sempre conseguiria vencer. No entanto, não gastei muito tempo computando ou configurando,então, temos o Pong AI, que ilustra as principais idéias e funciona muito bem:

.

.Também podemos observar os pesos obtidos da rede neural. Graças ao pré-processamento, cada uma de nossas entradas é uma imagem diferente de 80x80 (quadro atual menos quadro anterior). Cada neurônio da camada W1 é conectado a uma camada oculta W2 composta por 200 neurônios. O número de títulos é 80 * 80 * 200. Vamos tentar analisar essas conexões. Classificaremos todos os neurônios da camada W2 e visualizaremos quais pesos levam a ela. A partir das escalas que levam a um neurônio W2 dos neurônios W1, faremos imagens de 80x80. Abaixo estão 40 fotos desse tipo de W2 (um total de 200). Pixels brancos são pesos positivos e pretos são negativos. Observe que vários neurônios W2 estão sintonizados em uma bola voadora codificada em linhas tracejadas. Em um jogo, a bola pode estar apenas em um lugar,portanto, esses neurônios são polivalentes e "disparam" se a bola estiver em algum lugar dentro dessas linhas. A alternância de preto e branco é interessante, porque quando a bola se move ao longo da pista, a atividade do neurônio flutua como uma onda senoidal. E por causa da ReLU, ele apenas "dispara" em determinadas posições. Há muito ruído nas imagens, o que seria menor se eu usasse a regularização L2.

O que não está acontecendo. Então, aprendemos a jogar pong em imagens usando o gradiente da função policy, e isso funciona muito bem. Essa abordagem é uma forma bizarra de "sugerir e verificar", onde "adivinhar" se refere à execução de nossa política em vários episódios do jogo, e a "verificação" incentiva ações que levam a bons resultados. Em geral, isso representa o nível atual de como estamos lidando atualmente com os problemas do aprendizado reforçado. Se você entende o algoritmo intuitivamente e sabe como ele funciona, você deve ficar pelo menos um pouco decepcionado. Em particular, quando isso não funciona?

Compare isso com a forma como uma pessoa pode aprender a jogar pong. Você mesmo mostra o jogo a eles e diz algo como: “Você controla a raquete e pode movê-la para cima e para baixo, e sua tarefa é jogar a bola por outro jogador controlado pelo programa interno” e você está pronto para ir. Observe algumas diferenças:

- , , , . RL , . , ( ), , . . , , , , , , , , .
, ( , , , ..), ( «» « , , , - - . .). «» / . , , ( ) ( , ).
— (brute force), , . . , , , . , «» , . , , .
, , . , , . .

: : RL. , , . , . , 99% . , «» . : «», , - , - , - , , . « , ».

Eu também gostaria de enfatizar o fato de que, pelo contrário, em muitos jogos os gradientes da política derrotariam facilmente uma pessoa. Em particular, isso se aplica a jogos com recompensas frequentes, que exigem uma reação precisa e rápida e sem planejamento a longo prazo. Correlações de curto prazo entre recompensas e ações podem ser facilmente vistas pela abordagem do PG. Você pode ver semelhante em nosso agente Pong. Ele desenvolve uma estratégia quando simplesmente espera a bola e depois se move rapidamente para pegá-lo apenas na borda, por causa do qual a bola salta em alta velocidade vertical. O agente obtém várias vitórias consecutivas, repetindo essa estratégia simples. Existem muitos jogos (Pinball, Breakout) nos quais o Deep Q-Learning atrai e atropela uma pessoa na lama com suas ações simples e precisas.

Depois de entender o "truque" com o qual esses algoritmos funcionam, você poderá entender seus pontos fortes e fracos. Em particular, esses algoritmos estão muito atrás das pessoas na construção de idéias abstratas sobre jogos que as pessoas podem usar para um aprendizado rápido. Quando o computador olha para a matriz de pixels e percebe a chave, a porta e pensa consigo mesmo que provavelmente seria bom pegar a chave e chegar à porta. Atualmente, não há nada próximo disso, e tentar chegar lá é uma área ativa de pesquisa.

Cálculos não diferenciáveis em redes neurais.Gostaria de mencionar outra aplicação interessante de gradientes de política não relacionados a jogos: ela nos permite projetar e treinar redes neurais usando componentes que executam (ou interagem) com cálculos não diferenciáveis. Esta ideia foi introduzida pela primeira vez em 1992 por Williams . e foi recentemente popularizado em modelos recorrentes de atenção visual.chamado "atenção" no contexto de um modelo que processa uma imagem com uma sequência de aparência foveal estreita de baixa resolução, semelhante à maneira como nosso olho examina objetos com uma visão central em execução. A cada iteração, o RNN receberá um pequeno fragmento da imagem e selecionará o local que precisa ser mais analisado. Por exemplo, o RNN pode olhar para a posição (5.30), obter um pequeno fragmento da imagem e decidir olhar para (24, 50) etc. Há uma seção da rede neural que seleciona onde procurar mais e depois a inspeciona. Infelizmente, essa operação não é diferenciável, porque não sabemos o que aconteceria se levássemos uma amostra para outro lugar. Em um caso mais geral, considere uma rede neural que possui várias entradas e saídas:

Observe que a maioria das setas azuis é diferenciável como de costume, mas algumas transformações de exibição também podem incluir uma operação de seleção indiferenciada, destacada em vermelho. Podemos simplesmente percorrer as setas azuis na direção oposta, mas a seta vermelha é uma dependência pela qual não podemos inverter a propagação do backprop.

Política de gradiente para o resgate! Vamos pensar na parte da rede que realiza a amostragem que pode ser representada como uma função da política estocástica incorporada em uma grande rede neural. Portanto, durante o treinamento, produziremos vários exemplos (indicados pelos ramos abaixo) e, em seguida, incentivaremos amostras que acabam por levar a bons resultados (neste caso, por exemplo, medidos pela perda no final). Em outras palavras, treinaremos os parâmetros incluídos nas setas azuis usando o backprop, como de costume, mas os parâmetros incluídos na seta vermelha agora serão atualizados independentemente da passagem para trás usando gradientes de política, incentivando amostras que resultam em baixas perdas. Essa ideia também foi recentemente bem estruturada.Estimativa de gradiente usando gráficos de cálculo estocásticos.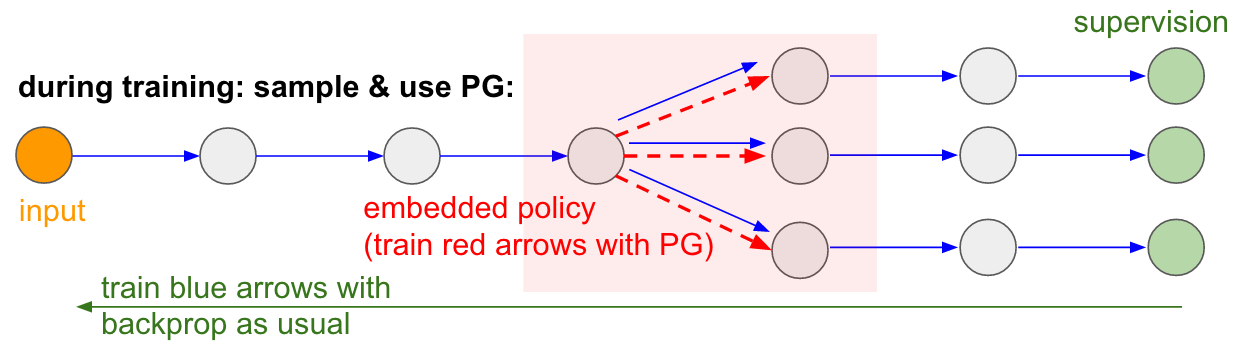

Entrada / saída treinada na memória de acesso aleatório. Você também encontrará essa idéia em muitos outros artigos. Por exemplo, a Neural Turing Machine possui uma fita de memória com a qual eles lêem e escrevem. Para executar uma operação de gravação, você precisa fazer algo como m [i] = x, onde ieex são previstos pela rede neural da RNN. No entanto, não há sinal nos dizendo o que aconteceria com a função de perda se escrevêssemos j! = I. Portanto, o NTM pode executar operações leves de leitura e gravação. Ele prevê a função de distribuição de atenção a e, em seguida, executa para todos i: m [i] = a [i] * x. Agora é diferenciável, mas temos que pagar um preço computacional alto, classificando todas as células.

No entanto, podemos usar gradientes de políticas para solucionar teoricamente esse problema, como é feito no RL-NTM. Ainda previmos a distribuição da atenção a, mas, em vez de uma busca exaustiva, selecionamos aleatoriamente os locais para escrever: i = amostra (a); m [i] = x. Durante o treinamento, poderíamos fazer isso por um pequeno conjunto de ie, no final, encontraríamos um conjunto que funcionaria melhor do que outros. Uma grande vantagem computacional é que, durante o teste, você pode ler / gravar em uma célula. No entanto, como indicado no documento, é muito difícil começar a trabalhar com essa estratégia, porque você precisa passar por muitas opções e quase acidentalmente acessar algoritmos de trabalho. Atualmente, os pesquisadores concordam que o PG funciona bem apenas quando existem várias opções discretas, quando você não precisa vasculhar espaços de pesquisa enormes.

No entanto, com a ajuda de gradientes de políticas e nos casos em que uma grande quantidade de dados e poder de computação está disponível, podemos, em princípio, sonhar muito. Por exemplo, podemos projetar redes neurais que aprendem a interagir com grandes objetos não diferenciáveis, como compiladores Latex. Por exemplo, para char-rnn gerar código Latex pronto, ou um sistema SLAM, ou solucionadores LQR, ou qualquer outra coisa. Ou, por exemplo, a superinteligência pode querer aprender a interagir com a Internet via TCP / IP (que também não é diferenciável) para acessar as informações necessárias para capturar o mundo. Este é um ótimo exemplo.

Conclusões

Vimos que os gradientes de políticas são um poderoso algoritmo geral e, por exemplo, treinamos o agente ATARI Pong a partir de pixels brutos do zero em 130 linhas Python . Em geral, o mesmo algoritmo pode ser usado para treinar agentes para jogos arbitrários e, esperançosamente, um dia podemos usá-lo para resolver problemas de controle no mundo real. Concluindo, gostaria de acrescentar mais alguns comentários:

Sobre o desenvolvimento da IA. Vimos que o algoritmo funciona por meio da pesquisa de força bruta, na qual você primeiro hesita aleatoriamente e precisa tropeçar em situações úteis pelo menos uma vez e, idealmente, com frequência, antes que a função política altere seus parâmetros. Também vimos que uma pessoa aborda essas soluções para esses problemas de uma maneira completamente diferente, que se assemelha à construção rápida de um modelo abstrato. Como esses modelos abstratos são muito difíceis (se não impossíveis) de se imaginar explicitamente, esse também é o motivo pelo qual recentemente houve tanto interesse em modelos generativos e indução de software.

Sobre o uso em robótica.O algoritmo não se aplica onde é difícil obter uma quantidade enorme de pesquisas. Por exemplo, você pode ter um (ou vários) robôs interagindo com o mundo em tempo real. Isso não é suficiente para uma aplicação ingênua do algoritmo. Uma área de trabalho projetada para mitigar esse problema são os gradientes determinísticos das políticas . Em vez de fazer tentativas reais, essa abordagem obtém informações de gradiente de uma segunda rede neural (chamada de crítica) que modela a função de avaliação. Essa abordagem pode, em princípio, ser eficaz com ações de alta dimensão, nas quais a amostragem aleatória fornece pouca cobertura. Outra abordagem relacionada é aumentar a robótica que estamos começando a ver no Google Robot Farmou talvez até em um Tesla S + com piloto automático.

Há também uma linha de trabalho que está tentando tornar o processo de pesquisa menos desesperador, adicionando controle adicional. Por exemplo, em muitos casos práticos, você pode obter a direção inicial do desenvolvimento diretamente da pessoa. Por exemplo, o AlphaGo primeiro usa o treinamento com um professor para prever apenas ações humanas (por exemplo , controle remoto de robô , aprendizado , otimização de trajetória , pesquisa completa de políticas ). E a política resultante é configurada posteriormente usando o PG para alcançar o objetivo real - vencer o jogo.

Em alguns casos, pode haver menos predefinições (por exemplo, para controlar remotamente os robôs ) e existem métodos para usar esses dados pré-estágio . Por fim, se as pessoas não fornecerem dados ou configurações específicas, elas também poderão ser obtidas em alguns casos através de cálculos usando métodos de otimização bastante caros, por exemplo, otimizando a trajetória em um modelo dinâmico conhecido (como F = ma em um simulador físico) ou em casos quando um modelo local aproximado é criado (como visto em uma estrutura muito promissora para pesquisa de política gerenciada).

Sobre o uso do PG na prática.Eu gostaria de falar mais sobre a RNN. Eu acho que pode parecer que as RNNs são mágicas e resolvem automaticamente problemas relacionados a seqüências arbitrárias. A verdade é que fazer com que esses modelos funcionem pode ser complicado. É necessário cuidado e experiência, além de saber quando métodos mais simples podem ajudá-lo a 90%. O mesmo vale para gradientes de políticas. Eles não funcionam automaticamente assim: você precisa ter muitos exemplos, eles podem treinar para sempre, são difíceis de depurar quando não funcionam. Você deve sempre tentar atirar de uma pistola pequena antes de pegar a Bazuca. Por exemplo, no caso de treinamento por reforço, o método de entropia cruzada (CEM) deve sempre ser verificado primeiro., uma abordagem estocástica simples de "adivinhar e verificar", inspirada na evolução. E se você insistir em experimentar gradientes de políticas para sua tarefa, verifique os truques específicos. Comece simples e use uma opção PG chamada TRPO , que quase sempre funciona melhor e com mais consistência do que o PG clássico . A idéia básica é evitar atualizar as configurações que alteram muito sua política, devido ao uso da distância Kulbak-Leibler entre a política antiga e a nova.

Isso é tudo!Espero ter lhe dado uma idéia de onde estamos com o Aprendizado por Reforço, quais são os problemas e, se você quiser ajudar a promover a RL, convido você a fazer isso no nosso OpenAI Gym :) Até a próxima!

Andrej Karpathy,
pesquisador, desenvolvedor, diretor do departamento de IA e piloto automático Tesla

Informações adicionais:

Deep Learning on Fingers Course 2018
https://habr.com/en/post/414165/ Deep Learning on Fingers

Open Course 2019
https: // habr.com/ru/company/ods/blog/438940/

Faculdade de Física da NSU
http://www.phys.nsu.ru/

Aprendizado profundo de reforço: pingue-pongue de pixel bruto

Conclusões

More articles: